【数据结构】排序算法精讲 | 插入排序全解：稳定性、复杂度与实战代码剖析

排序基本概念及直接插入排序

• 导读
• 一、排序的基本概念
• • [1.1 排序的定义](#1.1 排序的定义)
  • [1.2 排序算法的稳定性](#1.2 排序算法的稳定性)
  • [1.3 排序的分类](#1.3 排序的分类)
  • [1.4 内部排序算法](#1.4 内部排序算法)
• 二、插入排序
• • [2.1 插入排序的算法思想](#2.1 插入排序的算法思想)
  • [2.2 插入排序的个人理解](#2.2 插入排序的个人理解)
  • • 理解一：人脑运算的具象化排序
    • 理解二：扑克牌式排序
  • [2.3 插入排序的分类](#2.3 插入排序的分类)
• 三、C语言实现插入排序
• • [3.1 准备工作](#3.1 准备工作)
  • [3.2 函数三要素](#3.2 函数三要素)
  • [3.3 函数的实现------排序对象的划分](#3.3 函数的实现——排序对象的划分)
  • [3.4 函数的实现------待排序对象的插入](#3.4 函数的实现——待排序对象的插入)
  • [3.5 函数的实现------插入位置的查找](#3.5 函数的实现——插入位置的查找)
  • [3.6 时间复杂度分析](#3.6 时间复杂度分析)
  • [3.7 算法代码](#3.7 算法代码)
• 结语

导读

大家好，很高兴又和大家见面啦！！！

从今天开始，我们也将正式进入【数据结构】篇章的最后一章内容------排序。

排序相信大家都不陌生了，在学习C语言阶段，我们有接触过简单的 冒泡排序 以及如果借助库函数 qsort 来进行排序。从这两种排序的方式我们可以简单的将排序理解为------ 将无序的元素变为有序元素的过程 。

那具体什么是排序呢？排序又有哪些方法呢？在今天的内容中，我们将好好的认识一下排序，以及最简单的排序------插入排序。

一、排序的基本概念

1.1 排序的定义

排序 就是重新排列表中的元素，使表中的元素按关键字有序的过程 。

在查找中我们有介绍过，当元素在表中有序存储时，我们在查找的过程中能够更快的查找到目标元素。因此，为了查找方便，通常希望计算机中的表是按关键字有序的。排列的确切定义如下：

输入 ： n n n 个记录 R 1 、 R 2 、 ⋯ 、 R n R_1、R_2、\cdots、R_n R1、R2、⋯、Rn，对应的关键字为 k 1 、 k 2 、 ⋯ 、 k n k_1、k_2、\cdots、k_n k1、k2、⋯、kn。
输出 ：输入序列的一个重排 R 1 ′ 、 R 2 ′ ... ... R n ′ R_1'、R_2'......R_n' R1′、R2′......Rn′，使得其对应的关键字 k 1 ′ ≤ k 2 ′ ≤ ⋯ ≤ k n ′ k_1' \leq k_2' \leq \cdots \leq k_n' k1′≤k2′≤⋯≤kn′（其中 ≤ \bm{\leq} ≤ 可以换成其他的比较大小的符号）。

排序算法 我们更直观的理解就是，将输入的无序数据以有序的形式进行输出 ，当然，对于输入的有序数据而言，我们同样可以将其以自己需要的有序形式进行输出。

下面我们直接通过一个例子来进行理解，如下所示：

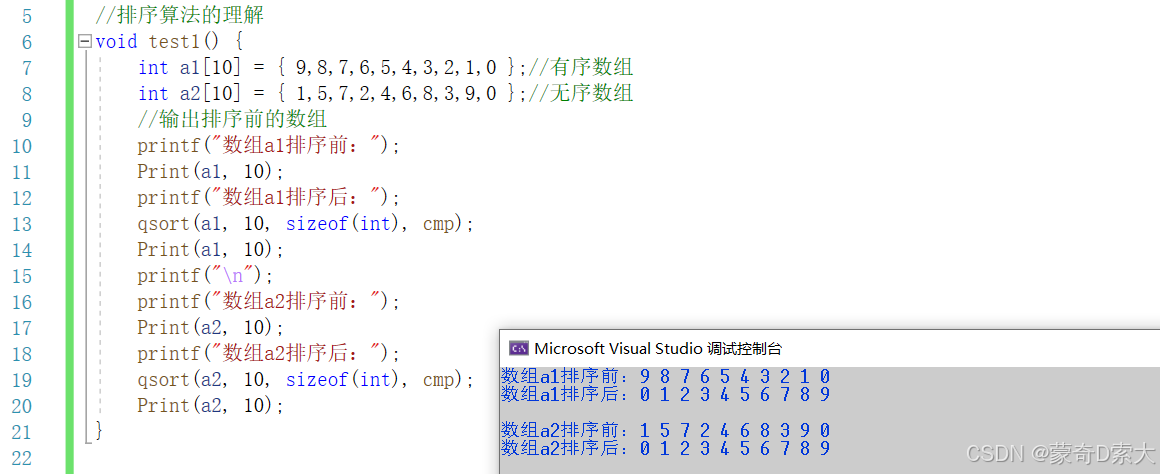
这里我们通过对 有序的数组 a1 与 无序数组 a2 通过 qsort 库函数来进行 升序排序 。从输出的结果可以看到，经过 排序 后的数组中的元素都按照要求在数组中完成了 升序排列 。同理，我们同样可以将数组完成 降序排序 ，具体的排序方式，则需要我们根据具体的情况进行选择。

排序在实际生活中也是应用广泛的一种方式，比如

• 我们在网购时，我们可以根据价格的升序来挑选商品，也可以根据价格的降序来挑选商品；
• 在学校里，老师会根据学生的考试情况来进行降序排列，并给排名靠前的学生给予一定的物质与精神奖励；
• 在公司里，老板会根据员工的工作业绩进行降序排列，并给业绩靠前的员工给予一定的物质奖励，给排序靠后的员工给予一定的精神鼓励......

因此 排序 对于程序猿来说，是一个必备的基本功。能否给数据进行排序，以及能否实现 高效的排序 ，这就很考验程序猿对 排序算法 的理解与运用的程度了。

1.2 排序算法的稳定性

在 排序算法 中，我们还需要关注一下不同排序算法的稳定性 。

所谓的排序算法的稳定性 ，指的是若待排序中有两个元素 R i R_i Ri 和 R j R_j Rj，其对应的关键字相同即 k e y i = k e y j key_i=key_j keyi=keyj ，且在排序前 R i R_i Ri 在 R j R_j Rj 的前面，在使用某一 排序算法 排序后， R i R_i Ri 仍然在 R j R_j Rj 的前面，则称这个 排序算法 是 稳定的 ，否则称排序算法是不稳定的。

下面我们通过一个具体的列子来理解 排序算法的稳定性，如下所示：

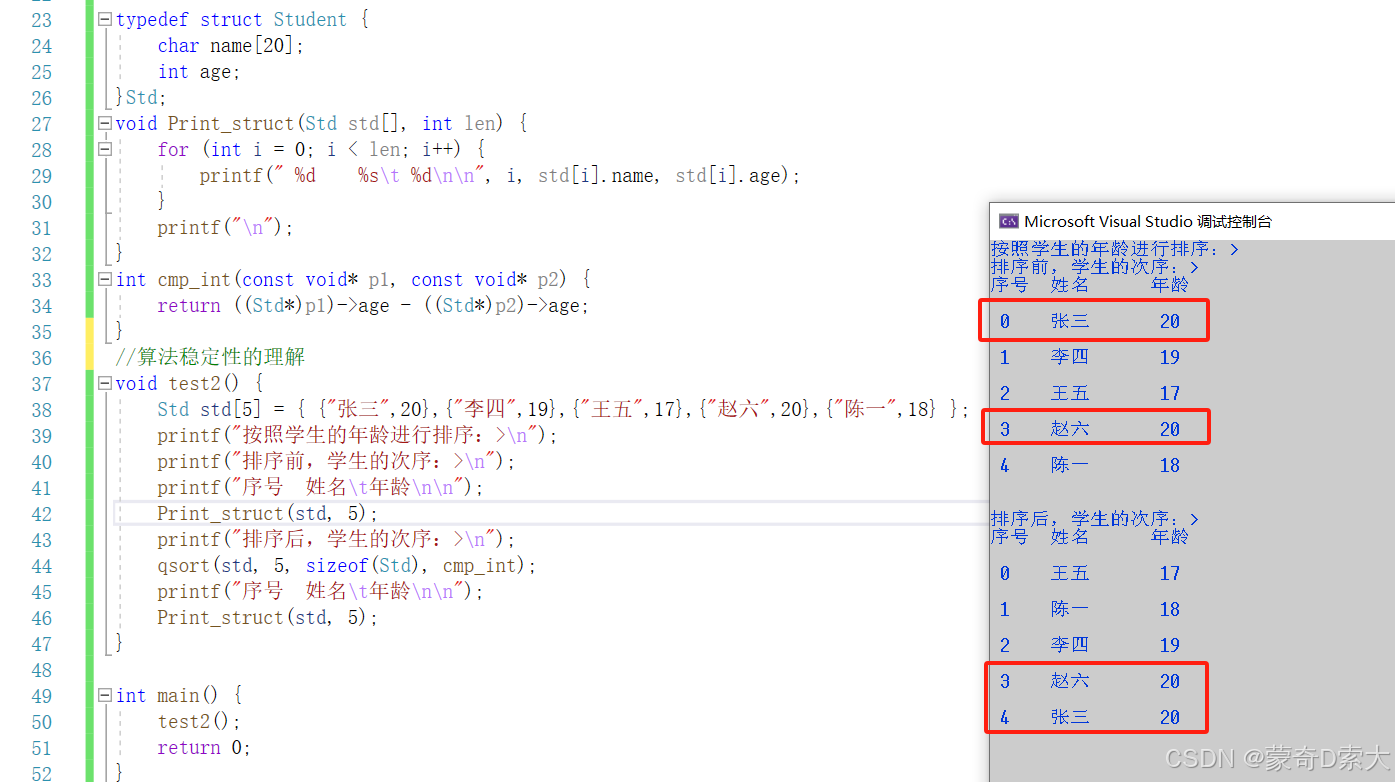
在这个例子中，我们通过按照年龄给 5 5 5 名学生进行排名，可以看到年龄同为 20 20 20 的张三和赵六，在排序前，张三的位置是在赵六的前面，但是经过排序后，张三则被排到了赵六的后面。

像 qsort 这种在排序完后会改变相同元素排序前的先后次序的算法 ，我们就将其称为 不稳定的排序算法 ；反之，如果在排序完后不改变相同元素的原先次序的算法 ，我们就称为 稳定的排序算法 。

需要注意的是，算法是否具有稳定性并不能衡量一个算法的优劣 ，他主要是对算法的性质进行描述。对于关键字唯一的待排序表而言，排序的结果是唯一的，那么选择排序算法时的稳定与否就无关紧要了。

在后续的学习中，当我们需要说明一个排序算法的不稳定性时，我们只需要像上例一样例举一组关键字的实例来说明它的不稳定性即可。

1.3 排序的分类

在排序算法中，也有不同种类的排序算法。根据排序表中的数据元素的存储位置，可以将排序算法分为两大类：

• 内部排序------数据都在内存中
• 外部排序------数据太多，无法全部放入内存

在本章节中，内部排序算法是我们重点学习的排序算法。一般情况下，内部排序算法在执行过程中都需要进行两种操作------比较与移动。

• 通过比较两个关键字的大小，确定对应元素的前后关系；
• 通过移动元素来使元素达到有序。

当然在内部排序算法中，也有一些是不需要进行比较的排序算法，如计数排序、基数排序、桶排序......

而外部排序算法主要是用于处理数据庞大无法通过内存将其全部进行存储的情况，这时，我们需要在排序的过程中根据要求不断地在内、外存之间数据的移动，以此来达到排序的目的。

在本章节中，我们会介绍三种外部排序算法------败者树、置换-选择排序以及最佳归并树。以及如何通过这三种算法来实现外部排序。

1.4 内部排序算法

在内部排序算法中，根据是否需要对元素进行比较可以将其分为两类------1.比较排序算法；2.非比较排序算法。

而比较排序算法中我们又可以根据比较与移动的方式的不同，进一步将其分为四大类：

• 插入排序
• 交换排序
• 选择排序
• 归并排序

对于非比较排序算法而言，我们只需要了解即可， 因此我们同样会介绍三种非比较排序算法：

• 计数排序
• 基数排序
• 桶排序

对于这些排序算法而言，都有各自的优缺点，我们不能对其进行明确的划分。在不同的环境下，都有其更为合适的排序算法，因此就其全面性而言，很难提出一种被认为最好的算法。

在排序算法中，算法的性能取决于算法的时间复杂度与空间复杂度，对于不同算法的时间复杂度的分析也是我们本章节中需要重点学习的内容。

在今天的内容中，我们会学习第一种内部排序算法------插入排序。

二、插入排序

插入排序是一种简单直观的排序方法，我们首先来了解一下算法的基本思想；

2.1 插入排序的算法思想

插入排序的算法大致可以分为五个步骤：

1. 将排序对象划分成三部分------左侧有序数据、待排序对象以及右侧无序数据。
2. 记录待排序对象的数据
3. 在左侧有序数据中查找待排序对象的位置
4. 按排序对象在左侧有序数据中的位置插入待排序对象
5. 重复上述步骤，直到右侧无序数据全部完成排序

将该排序思想总结为一句话就是------每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插入完成。具体排序过程如下所示：

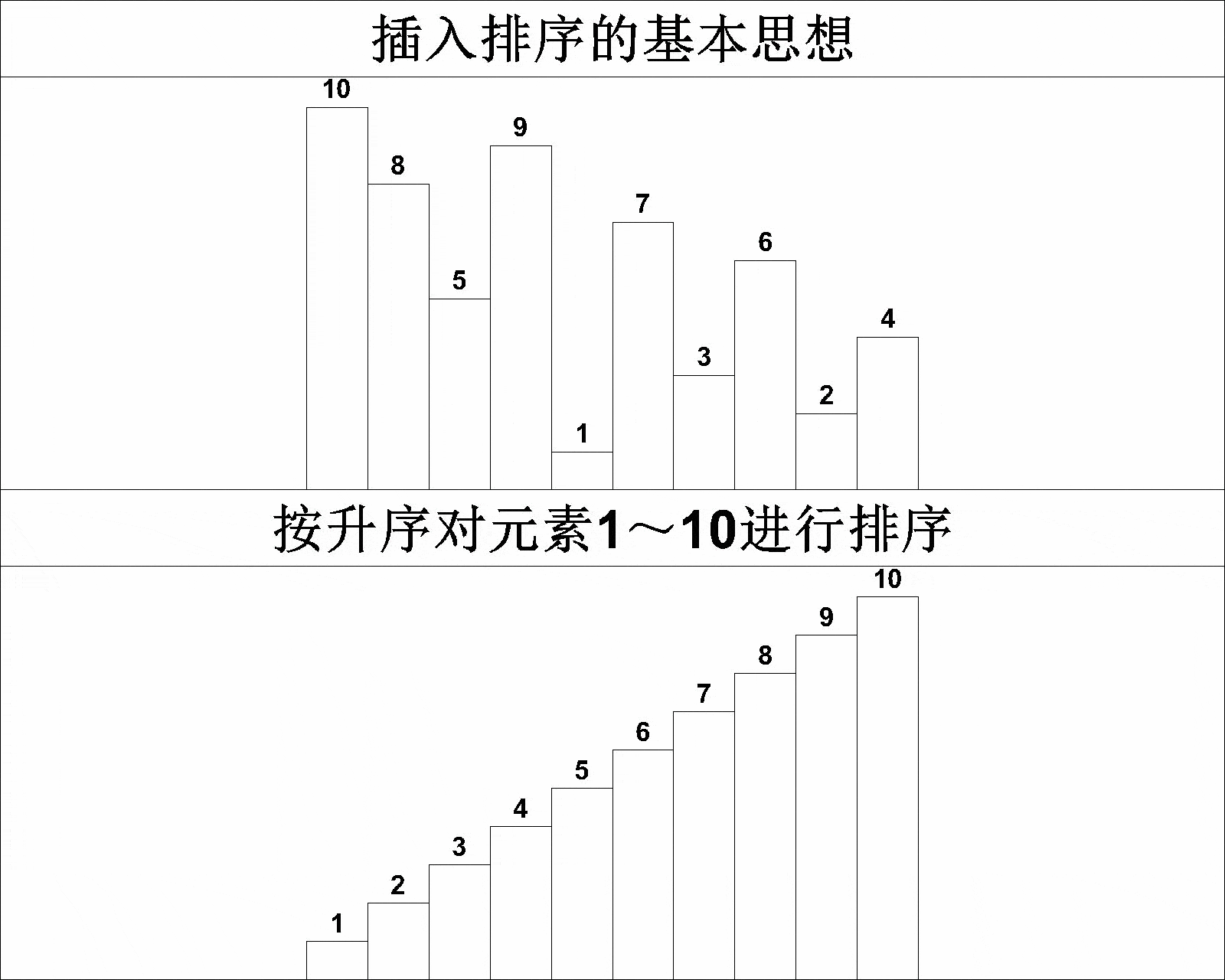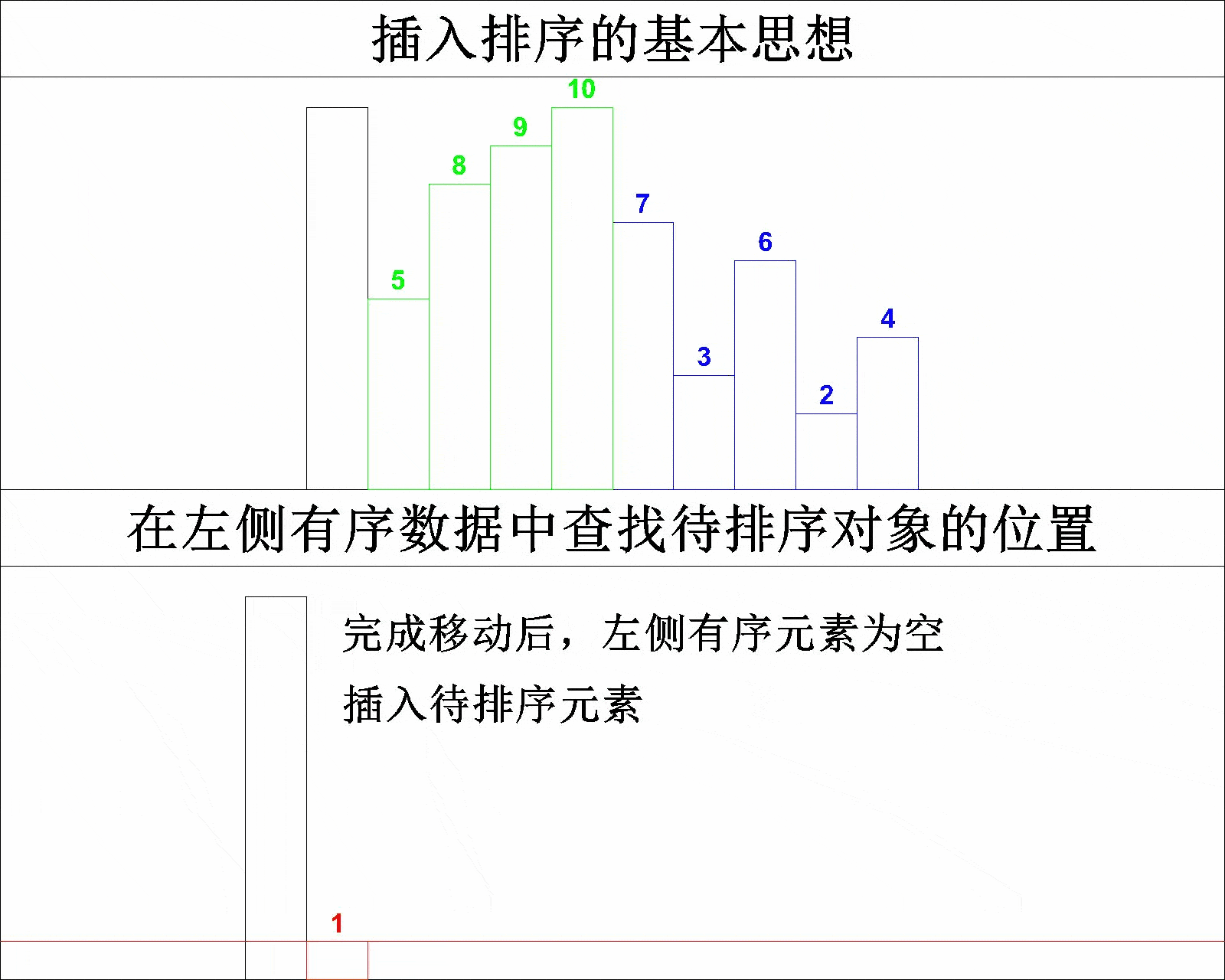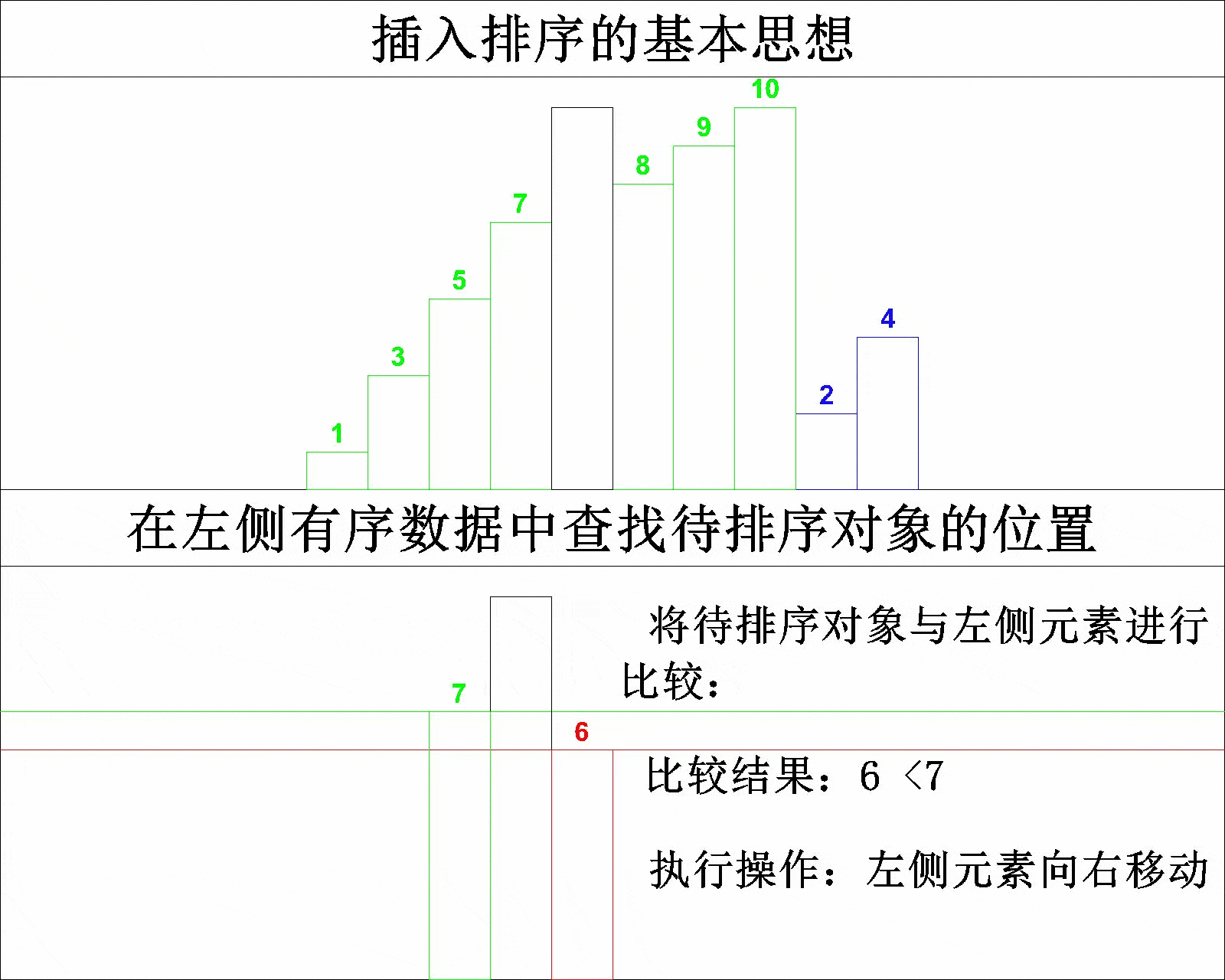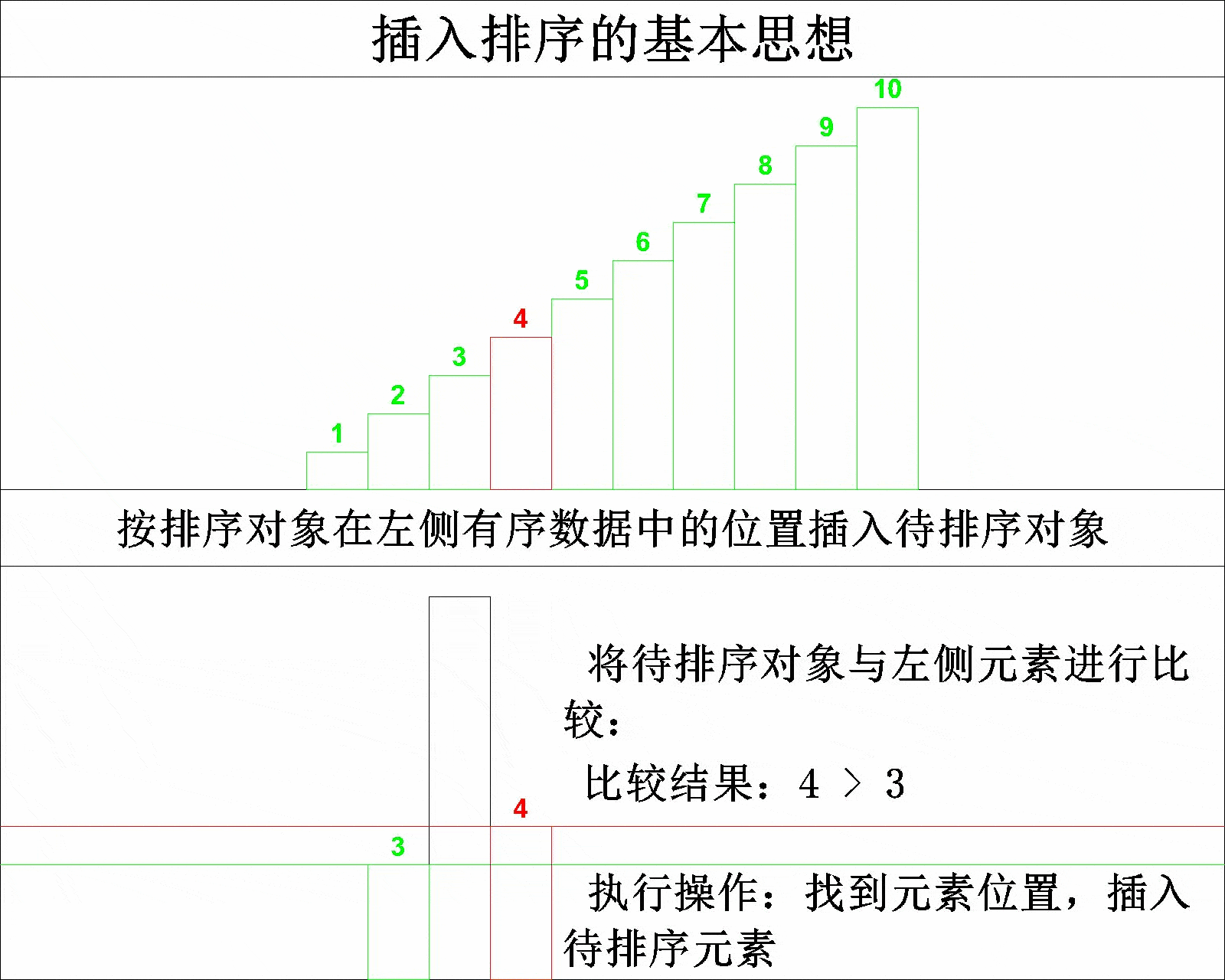
相信大家看到上图的演示，应该能够理解插入排序的基本思想了。

---

下面我给大家介绍一下我对插入排序的几种理解，大家可以选择自己更容易接受的方式来理解插入排序，当然也可以直接跳过这个部分，这也只是我个人对该排序算法的理解，并不能代表该排序算法；

2.2 插入排序的个人理解

理解一：人脑运算的具象化排序

之所以说插入排序时人脑运算的具象化排序，这是因为当我们在扫描一组无序数据并进行排序时，对于数据量少的数据我们可以很轻易的完成排序，如下所示：

以这张图为例，下面我们一起来做一个简单的实验：

1. 首先我们用一张不透明的纸挡住上图
2. 接着我们从左往右慢慢移动这张纸
3. 之后每次看到一个数据时，我们直接给这些数据进行排序
4. 最后在完成所有数据排序的过程中我们需要关注我们的大脑是如何完成数据排序的

如果有跟着一起做这个实验的朋友，我们会发现，当我们的大脑在对这些数据进行排序时，我们的大脑能够迅速的找到每一个数据的正确位置，并完成数据的插入。

然后我们再来看插入排序的算法思路，有没有发现，它跟我们的大脑进行排序时的思路是一致的，因此我对插入算法的第一个理解是通过计算机语言来实现大脑进行排序时的具象化。

理解二：扑克牌式排序

不知道大家有没有玩过扑克牌，比如斗地主。

当我们在摸牌阶段，我们是一张牌一张牌的拿到手中，在拿下一张牌前，大部分的朋友应该会和我一样，将新拿到手的牌根据它的正确位置插入到手牌中。

我的习惯是按照牌的降序进行排列，因此当我手中有一张4时，我摸到了一张3，我就会将其插入4的右侧，当我摸到一张比4大的牌时，我则会将其插入4的左侧。像我们在斗地主时对手牌进行排序的过程就是进行插入排序的过程。

---

2.3 插入排序的分类

当我们通过C语言来实现插入排序的整个过程时，根据具体的实现方式的不同，我们可以将插入排序分为三种：

1. 直接插入排序------按照插入排序的算法思想，直接通过C语言来实现完整的插入排序；
2. 折半插入排序------在直接插入排序的算法思想下，对算法进行优化；
3. 希尔排序------在直接插入排序的算法思想下，对算法进行进一步的优化；

在今天的内容中我们会重点介绍如何实现直接插入排序以及对直接插入排序算法的复杂度分析；

三、C语言实现插入排序

3.1 准备工作

在实现插入排序前，我们可以先创建好三个文件：

• 排序算法实现文件Sort.c------用于进行排序算法的实现
• 排序算法头文件Sort.h------用于进行排序算法的声明
• 排序算法测试文件test.c------用于测试排序算法

这里我的个人习惯是将具体的算法实现与测试文件分成两个文件，当然每个人的编程习惯都不相同，大家可以根据自己的习惯来进行具体的文件创建工作。

3.2 函数三要素

在排序算法中，我们同样要确定函数名、函数参数以及函数的返回类型：

• 函数名------函数的命名在一定程度上可以反映该函数的具体功能，因此对于插入排序算法的函数名，我们可以将其命名为InsertSort；
• 函数的参数------排序算法的参数主要是2个内容：需要排序的对象以及排序对象的元素个数。在函数运行的过程中，会涉及到对排序对象的修改，因此插入排序的函数参数我们可以将其定为指向排序对象的指针ElemType* a与反映排序对象中元素个数的整型int len；
• 函数的返回类型------对于排序函数而言，我们需要的就是它能够正常的实现排序的功能，而排序的实现并不需要任何的返回值，因此我们可以将排序算法的返回值定为void；

//插入排序------直接插入排序
void InsertSort(ElemType* a, int len) {

}

3.3 函数的实现------排序对象的划分

在插入排序的算法思想中，算法的第一步是将排序对象进行划分，将其划分成三个部分：

• 左侧有序
• 待排序对象
• 右侧无序

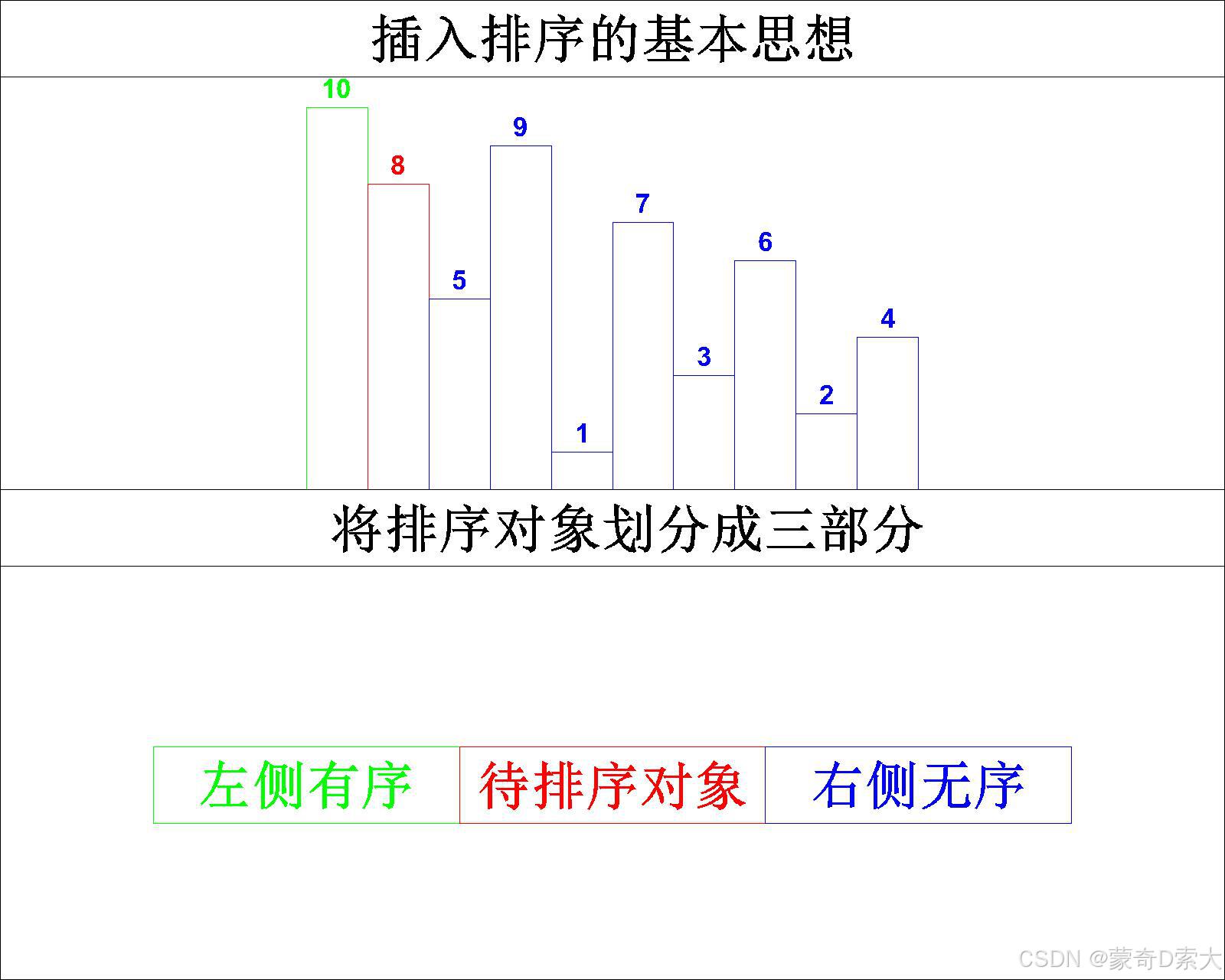
对于不同的排序对象，我们有不同的划分方式，这里以顺序表为例，我们可以通过数组下标来对数组空间中的元素进行一个分区，如下所示：

当我们要对上图所示的对象进行插入排序时，我们是从首元素开始进行依次的插入，但是首元素的左侧已经没有其他元素了，因此在第一趟排序中我们可以直接默认首元素时左侧的有序元素，第二个元素则是待排序的对象，从第三个元素开始就为右侧的无序元素。

在顺序表中首元素对应的下标为0，待排序对象对应的下标为1，右侧无序元素的开始下标为2。以这个思路，我们不妨直接通过下标来反映元素的分区，如下所示：

	//对排序对象进行划分
	int left = 0, key = 1, right = 2;

当然我们要完成所有元素的插入排序时，仅仅对第一趟的排序进行分区是远远不够的，下面假设我们已经完成了多趟的排序，对剩下的未排序元素进行排序前的划分如下所示：

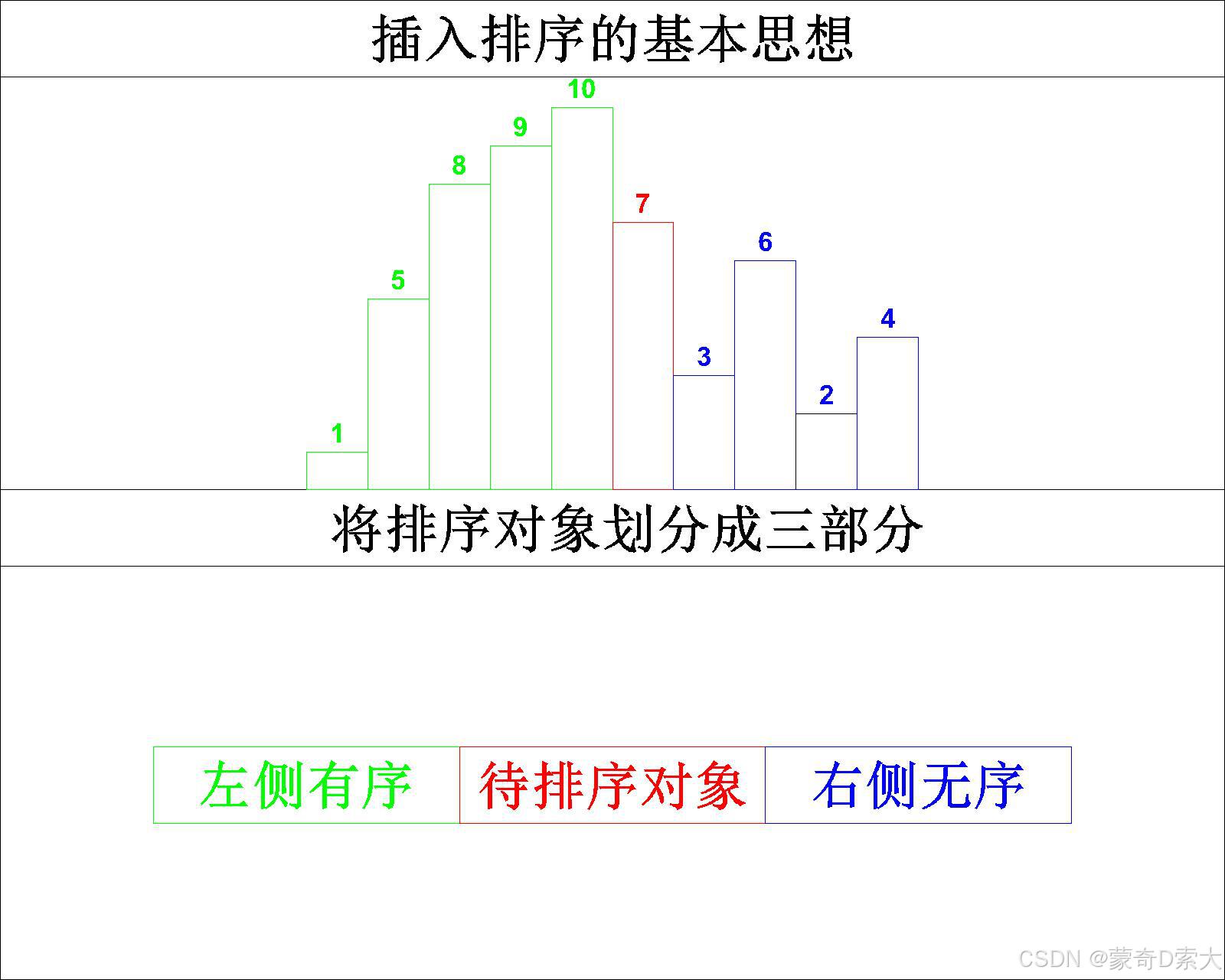
从上图中我们可以看到，此时左侧的有序元素已经有了5个，右侧的无序元素只剩4个，当我们对其进行划分时，左侧有序元素与待排序对象的分界线应该是元素10，其对应的下标4，待排序对象对应的元素下标为5，右侧无序元素的起点应该是元素3，其所对应的下标为6；

从这里我们不难发现，在整个插入排序的过程中，对于有n个元素的排序对象，以待排序对象为分界线的话，其对应的下标为x，那么左侧有序对象的起点则为x - 1，终点为0，右侧无序对象的起点为x + 1，终点为n - 1。

在理清了分区之间的关系后，接下来我们要思考如何完成每一趟排序的划分。

从前面的演示过程我们不难发现，在整个排序的过程中，对于右侧的无序元素，我们并不需要对其进行任何操作，我们真正需要进行操作的对象是待排序对象的记录与左侧有序元素的移动以及待排序对象的插入。

因此我们在具体的实现过程中，可以从待排序对象与左侧有序元素的起点二者中选取一个作为分界点，如下所示：

	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len - 1; i++) {
		int key = i + 1;//待排序对象所对应的下标
	}
	//以待排序对象作为分界线对排序对象进行划分
	for (int key = 1; key < len; key++) {
		int i = key - 1;//左侧有序元素的起点
	}

这两种划分的方式都是可取的，可以根据自己的习惯进行选择，这里我选择的是第1中，以左侧有序对象的起点作为分界线来划分排序对象。在完成划分后，我们需要对待排序对象进行记录，这里直接通过变量来存储待排序对象即可，如下所示：

	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len; i++) {
		//记录需要排序的元素
		ElemType key = a[i + 1];
	}

3.4 函数的实现------待排序对象的插入

在完成排序对象的划分与待排序对象的记录后，接下来我们需要完成的就是2个功能：

• 待排序对象插入位置的查找
• 待排序对象的插入

在顺序表中元素的插入实际上就是对相应下标的空间进行赋值，这个比较简单，在链表中，我们则需要改变插入结点的指针与其前驱结点的指针，如下所示：

	//链表的插入
	//p------指向待插入结点的指针
	//q------待插入结点的前驱结点指针
	p->next = q->next;
	q->next = p;

因为不管是顺序表还是链表，在插入前我们都需要进行查找操作，因此链表中可以在查找的同时记录待插入位置的前驱结点来完成插入。

对链表的基本操作不太熟悉的朋友可以回顾一下【数据结构】C语言实现单链表的基本操作的内容，这里我就不再展开赘述。

接下来我们要重点介绍一下查找的实现。

3.5 函数的实现------插入位置的查找

在整个查找的过程中，我们是从起点开始往后查找，当没有找到具体位置时，需要对已查找的元素往右移动，同时继续向左查找，这时就会有两种情况：

• 左侧元素全部查找完------此时我们需要直接将待排序对象插入到首元素的位置
• 在左侧元素中找到具体的插入位置------此时我们不需要继续查找，并将待排序对象插入到查找到的位置

这个功能的实现并不复杂，如下所示：

		//插入位置的查找
		int j = i;//记录左侧有序元素的起点
		//j < 0时表示查找完左侧所有元素
		//a[j] <= key时表示找到了元素需要进行插入的位置
		while (j >= 0 && a[j] > key) {
			a[j + 1] = a[j];//元素向后移动
			j -= 1;//移动查找指针
		}
		//插入元素
		a[j + 1] = key;

现在我们就完成了插入排序所有代码的编写，接下来我们就来测试一下插入排序，如下所示：

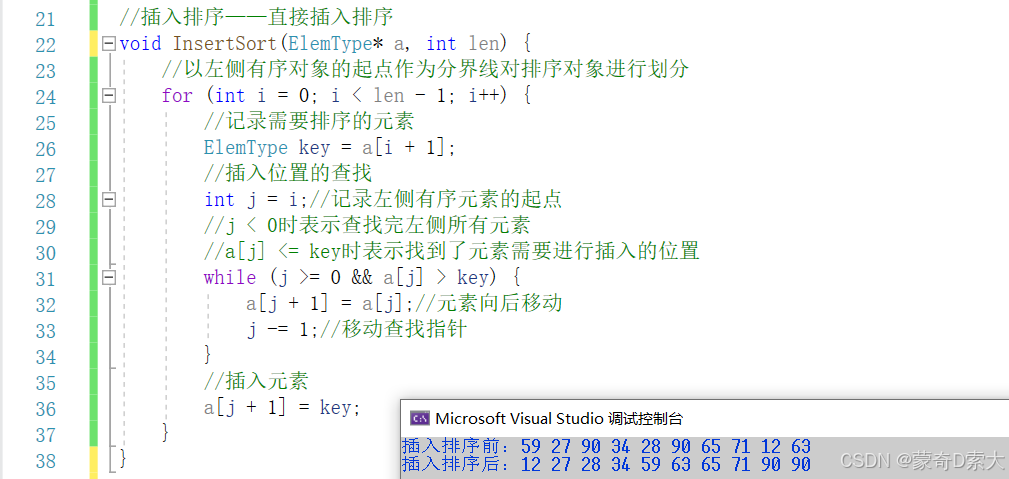
可以看到，此时我们很好的实现了排序的功能。接下来我们就来分析一下插入排序算法的时间复杂度

3.6 时间复杂度分析

在插入排序中，主要有两个功能需要消耗时间，一个是遍历排序对象，对于有n个元素的排序对象而言，算法需要遍历n-1个元素；

在每一趟遍历中，还需要执行查找操作，根据查找的过程，总共有三种情况：

• 最好情况------元素有序排列，每次查找只需要执行一次。对于n-1个元素而言，总的查找次数就是n-1，对应的最好时间复杂度------ O ( N ) O(N) O(N)
• 最坏情况------元素逆序排列：
  • 第一个元素需要查找1次
  • 第二个元素需要查找2次
  • 第三个元素需要查找3次
  • ......
  • 第n - 1个元素需要查找n - 1次

总的查找次数为 1 + 2 + 3 + ... ... + ( n − 1 ) = n ( n − 1 ) / 2 = ( n 2 − n ) / 2 1 + 2 + 3 + ......+ (n - 1) = n(n - 1)/2 = (n^2-n)/2 1+2+3+......+(n−1)=n(n−1)/2=(n2−n)/2，对应的最坏时间复杂度： O ( N 2 ) O(N^2) O(N2)

• 平均情况下，每一次查找次数都不太确定，第 i 个元素的查找次数是从1 ～ i次，对于n - 1个元素而言，总的查找次数为(n - 1) ～ n*(n - 1)/2次，对应的平均时间复杂度： O ( N 2 ) O(N^2) O(N2)

在插入排序算法中，我们消耗了2个整型空间来存储下标，一个元素对应类型的空间来存储待插入的元素，以这里的整型元素为例，总共消耗的空间为12个字节，对应的空间复杂度： O ( 1 ) O(1) O(1)。

3.7 算法代码

下面给大家展示一下从算法的实现到头文件再到测试的完整代码：

//Sort.c
void Print(ElemType A[], int len) {
	for (int i = 0; i < len; i++) {
		printf("%d ", A[i]);
	}
	printf("\n");
}
//插入排序------直接插入排序
void InsertSort(ElemType* a, int len) {
	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len - 1; i++) {
		//记录需要排序的元素
		ElemType key = a[i + 1];
		//插入位置的查找
		int j = i;//记录左侧有序元素的起点
		//j < 0时表示查找完左侧所有元素
		//a[j] <= key时表示找到了元素需要进行插入的位置
		while (j >= 0 && a[j] > key) {
			a[j + 1] = a[j];//元素向后移动
			j -= 1;//移动查找指针
		}
		//插入元素
		a[j + 1] = key;
	}
}

//sort.h
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>
#include <assert.h>

typedef int ElemType;
//元素打印
void Print(ElemType A[], int len);
//插入排序------直接插入排序
void InsertSort(ElemType* a, int len);

//test.c
//直接插入排序算法的测试
void test3() {
	srand(time(NULL));
	int N = 10;
	int* a = (int*)calloc(N, sizeof(int));
	assert(a);
	for (int i = 0; i < N; i++) {
		a[i] = rand() % 100;
	}

	printf("插入排序前：");
	Print(a, N);
	printf("插入排序后：");
	InsertSort(a, N);
	Print(a, N);

	free(a);
}

int main() {
	test3();
	return 0;
}

有需要的朋友可以自取进行测试。

结语

在今天的内容中我们介绍了 排序的基本概念 ：

• 重新排列表中的元素，使表中的元素按关键字有序的过程。

在 排序算法 中，我们需要关注其 稳定性：

• 排序后会改变相同元素排序前的先后次序，则称为 不稳定
• 排序后不改变相同元素排序前的先后次序，则称为 稳定

排序算法 按 数据元素的存储位置 可以分为：

• 内部排序 ------ 数据都存储于内存中
• 外部排序 ------ 数据存储于外部磁盘中

内部排序 算法根据是否需要进行 比较 操作，可以分为：

• 比较排序算法
• 非比较排序算法

比较排序算法大多都需要执行两种操作：

• 比较：比较两个关键字的大小，确定关键字的前后关系
• 移动：移动关键字使其达到有序

在比较排序算法中，根据比较和移动的方式的不同，又可以进一步分为四大类：

• 插入排序
• 交换排序
• 选择排序
• 归并排序

我们需要了解的非比较排序算法主要有三种：

• 计数排序
• 基数排序
• 桶排序

插入排序是一种简单直观的排序方法，其算法思想为：

• 将待排序的记录按照其关键字大小插入到以及排好序的子序列中，直到完成全部记录的插入。

插入排序按照具体的实现方式，又可以分为三类：

• 直接插入排序
• 折半插入排序
• 希尔排序

今天我们重点介绍了 直接插入排序 的C语言实现，该排序算法属于稳定的排序算法 ，其 时间复杂度 为：

• 最好情况： O ( N ) O(N) O(N)
• 最坏情况： O ( N 2 ) O(N^2) O(N2)
• 平均情况： O ( N 2 ) O(N^2) O(N2)

其 空间复杂度 为： O ( 1 ) O(1) O(1)

接下来我们将逐一介绍其它的排序算法，大家记得关注哦！

互动与分享

• 点赞👍 - 您的认可是我持续创作的最大动力

• 收藏⭐ - 方便随时回顾这些重要的基础概念

• 转发↗️ - 分享给更多可能需要的朋友

• 评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！ 关注博主，不错过更多技术干货。我们下一篇再见！