【Python进阶】数据结构的精巧与算法的智慧：AI提速的关键

[1. Python内置数据结构的高级用法](#1. Python内置数据结构的高级用法)

[1.1. list, tuple, dict, set 的性能特点与适用场景](#1.1. list, tuple, dict, set 的性能特点与适用场景)

[1.2. collections 模块：AI数据处理的利器](#1.2. collections 模块：AI数据处理的利器)

[2. 理解常见算法](#2. 理解常见算法)

[2.1. 排序算法（快速排序、归并排序）的原理与Python实现](#2.1. 排序算法（快速排序、归并排序）的原理与Python实现)

[2.2. 查找算法（二分查找）的应用](#2.2. 查找算法（二分查找）的应用)

[2.3. 理解时间复杂度和空间复杂度](#2.3. 理解时间复杂度和空间复杂度)

[3. 算法在AI中的应用](#3. 算法在AI中的应用)

[3.1. 数据预处理中的排序、去重](#3.1. 数据预处理中的排序、去重)

[3.2. 图算法在某些AI问题中的应用](#3.2. 图算法在某些AI问题中的应用)

[3.3. 搜索算法在AI决策过程中的体现](#3.3. 搜索算法在AI决策过程中的体现)

[4. NumPy 深度解析](#4. NumPy 深度解析)

[4.1. N-dimensional array (ndarray) 的创建、索引、切片](#4.1. N-dimensional array (ndarray) 的创建、索引、切片)

[4.2. 向量化操作 (Vectorization) 与广播 (Broadcasting) 机制](#4.2. 向量化操作 (Vectorization) 与广播 (Broadcasting) 机制)

[4.3. NumPy 的数学函数库](#4.3. NumPy 的数学函数库)

[5. 小结与AI启发](#5. 小结与AI启发)

在人工智能（AI）飞速发展的浪潮中，模型性能的提升固然是焦点，但支撑起这一切的底层基石------数据结构和算法的效率，却往往被忽视。一个精心设计的数据结构，能够以最优的方式组织和访问数据，而一个高效的算法，则能在海量数据中迅速找到问题的解决方案。这两者的精巧结合，构成了AI提速的强大引擎。本文将深入探讨Python内置数据结构的高级用法，理解常见算法的原理与复杂度，剖析算法在AI领域的具体应用，并详细解析NumPy这一AI计算的基石，最终揭示数据结构与算法在AI提速中的关键作用。

1. Python内置数据结构的高级用法

Python作为一种高级编程语言，其内置的数据结构以其易用性和灵活性而著称。然而，深入理解这些数据结构的性能特点和适用场景，能够极大地优化AI数据处理的效率。

1.1. `list`, `tuple`, `dict`, `set` 的性能特点与适用场景

list (列表): Python中最常用的序列类型，是可变的（mutable）。列表的优点在于其灵活性，可以存储不同类型的数据，并且支持动态增删。然而，在需要频繁插入或删除元素（尤其是在列表的开头或中间）时，list 的性能会受到影响，因为这可能需要移动大量的后续元素，其时间复杂度通常为 O(n)。在AI数据处理中，列表常用于存储一序列的样本、特征向量或者中间计算结果。例如，一个包含多个图像像素值的列表，或者一个包含模型训练过程中损失值的列表。当需要对数据进行顺序访问、修改或追加时，list 是一个不错的选择。
tuple (元组): 与列表类似，元组也是序列类型，但它是不可变的（immutable）。这意味着一旦创建，元组中的元素就不能被修改。这种不可变性带来了性能上的优势，元组的创建和访问通常比列表更快，并且由于其固定性，可以作为字典的键（key），或者在集合（set）中使用。在AI领域，元组常用于表示固定长度的数据记录，例如一个样本的坐标 (x, y)，或者模型的权重和偏置 (weight, bias)。当数据的完整性至关重要，或者需要将数据作为哈希表的键时，元组是更优的选择。
dict (字典): 字典是一种键值对（key-value）的无序集合，是可变的。字典的核心优势在于其快速查找能力，通过哈希表实现，平均查找、插入和删除操作的时间复杂度为 O(1)。这使得字典在需要根据特定标识符快速检索数据时非常有用。在AI中，字典的应用极为广泛：可以用来存储模型的参数（例如，层名作为键，对应的权重矩阵作为值），也可以用来表示具有命名属性的数据（例如，一个样本的特征字典，键是特征名，值是特征值），或者用于统计词频、计数等场景。
set (集合): 集合是无序的，且不允许重复元素的集合。集合的优势在于其快速的成员资格测试（membership testing）、集合的并集、交集、差集等操作，这些操作的平均时间复杂度也接近 O(1)。在AI数据处理中，集合常用于去重，例如，在处理文本数据时，可以使用集合来存储所有不重复的词汇；或者在图算法中，用集合来记录已访问的节点，避免重复访问。

1.2. `collections` 模块：AI数据处理的利器

Python的 collections 模块提供了许多比内置数据结构更专业、更高效的容器类型，它们在AI数据处理中扮演着重要角色。

collections.defaultdict: defaultdict 是 dict 的一个子类，它在访问不存在的键时不会引发 KeyError，而是会调用一个工厂函数（factory function）来为该键生成一个默认值，并将其插入字典。这极大地简化了在处理分组、计数或累加数据时的代码。例如，在构建词汇表时，可以使用 defaultdict(set) 来存储每个词汇出现的所有文档ID，或者使用 defaultdict(int) 来统计词频。
collections.Counter: Counter 是一个特殊的字典子类，用于计数可哈希对象。它可以方便地统计列表中元素的出现次数，并支持直接进行计数运算（如加法、减法）。在自然语言处理（NLP）中，Counter 是计算词频、N-gram 频率的绝佳工具。例如，Counter(words) 可以快速得到一个词语的频率分布。
collections.deque (双端队列): deque 是一个双端队列，支持在两端（头部和尾部）进行 O(1) 时间复杂度的添加和删除操作。这使得 deque 在需要实现队列、栈或者在固定大小的窗口内进行数据滑动时非常高效。在AI中，deque 可以用于实现广度优先搜索（BFS）中的队列，或者在序列数据处理中维护一个固定大小的历史窗口。
collections.namedtuple: namedtuple 是一个工厂函数，用于创建具有命名属性的元组子类。它使得访问元组中的元素可以通过属性名（如 point.x）而不是索引（如 point[0]），提高了代码的可读性和可维护性。在AI中，namedtuple 可以用来表示具有固定结构的数据记录，例如一个训练样本，包含特征、标签和权重等信息，使用 Sample(features=..., label=..., weight=...) 比 (features, label, weight) 更易于理解。

2. 理解常见算法

算法是解决问题的步骤和方法，其效率直接影响程序的运行速度和资源消耗。理解算法的核心思想、实现方式以及其时间、空间复杂度，是进行AI优化的基础。

2.1. 排序算法（快速排序、归并排序）的原理与Python实现

排序是将一组数据按照特定顺序排列的过程。高效的排序算法对于数据预处理、数据检索以及许多其他算法的实现至关重要。

快速排序 (Quicksort): 快速排序是一种分治（divide and conquer）的排序算法。其基本思想是选择一个"基准"（pivot）元素，然后将数组分区（partition），使得所有小于基准的元素都位于基准的左边，所有大于基准的元素都位于基准的右边。这个过程递归地应用于左右两个子数组，直到整个数组有序。
- 原理:
  1. 选择一个基准元素（通常是数组的第一个、最后一个或中间元素）。
  2. 重新排列数组，使得所有小于基准的元素都在基准之前，所有大于基准的元素都在基准之后。这个过程称为分区（partition）。
  3. 递归地对基准左边和右边的子数组进行快速排序。
- 时间复杂度: 平均情况下为 O(n log n)，最坏情况下（当基准选择不当时，例如每次都选择最小或最大的元素）为 O(n^2)。
- Python实现示例 (概念性):
  复制代码
```
def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)
```
  注意：这是一个简洁的Pythonic实现，但其空间复杂度较高。更经典的原地分区实现会更节省空间。
归并排序 (Mergesort): 归并排序也是一种分治算法，它将数组递归地分成两半，直到每个子数组只有一个元素（此时认为是已排序的），然后将这些有序的子数组合并（merge）成更大的有序数组，直到整个数组有序。
- 原理:
  1. 如果数组长度小于等于1，则已排序。
  2. 将数组分成两半。
  3. 递归地对左半部分和右半部分进行归并排序。
  4. 将两个已排序的子数组合并成一个有序数组。合并过程需要一个额外的空间来存储临时结果。
- 时间复杂度: 始终为 O(n log n)，无论输入数组的初始状态如何。
- 空间复杂度: O(n)，因为合并过程需要额外的空间。
- Python实现示例 (概念性):
  复制代码
```
def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]

    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)

    return merge(left_half, right_half)

def merge(left, right):
    merged = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1
    merged.extend(left[i:])
    merged.extend(right[j:])
    return merged
```

2.2. 查找算法（二分查找）的应用

查找是在数据集合中寻找特定元素的算法。

二分查找 (Binary Search): 二分查找是一种非常高效的查找算法，但它要求被查找的序列必须是有序的。其原理是不断地将查找区间缩小一半。
- 原理:
  1. 从有序序列的中间元素开始查找。
  2. 如果中间元素正好是要查找的元素，则查找成功。
  3. 如果查找元素小于中间元素，则在序列的前半部分继续查找。
  4. 如果查找元素大于中间元素，则在序列的后半部分继续查找。
  5. 重复这个过程，直到找到元素或查找区间为空。
- 时间复杂度: O(log n)。
- 应用: 在AI中，二分查找可以用于在有序的特征向量、参数列表或查找表中快速定位信息。例如，在某些推荐系统中，可以对用户或物品的向量进行排序，然后用二分查找来快速匹配相似项。

2.3. 理解时间复杂度和空间复杂度

时间复杂度 (Time Complexity): 用来衡量算法执行时间随输入规模增长而增长的趋势。常用大O符号（Big O notation）表示，如 O(1), O(log n), O(n), O(n log n), O(n^2), O(2^n) 等。
- O(1) - 常数时间: 算法执行时间不随输入规模变化。例如，访问列表中的某个元素。
- O(log n) - 对数时间: 算法执行时间随输入规模的对数增长。例如，二分查找。
- O(n) - 线性时间: 算法执行时间与输入规模成正比。例如，遍历列表。
- O(n log n) - 线性对数时间: 常见的排序算法（如快速排序、归并排序）的平均时间复杂度。
- O(n^2) - 平方时间: 算法执行时间与输入规模的平方成正比。例如，简单的冒泡排序或嵌套循环。
- O(2^n) - 指数时间: 算法执行时间随输入规模呈指数增长，通常效率很低，只适用于小规模问题。
空间复杂度 (Space Complexity): 用来衡量算法执行过程中所需要的额外存储空间随输入规模增长而增长的趋势。同样使用大O符号表示。
- O(1) - 常数空间: 算法所需的额外空间不随输入规模变化。
- O(n) - 线性空间: 算法所需的额外空间与输入规模成正比。例如，归并排序需要额外的空间来合并子数组。

在AI领域，尤其是在处理大规模数据集和复杂模型时，选择具有较低时间复杂度和空间复杂度的算法至关重要，直接关系到模型的训练速度、推理速度以及部署的可行性。

3. 算法在AI中的应用

算法是AI的核心驱动力，它们被广泛应用于数据的处理、模型的构建和决策的制定。

3.1. 数据预处理中的排序、去重

在将原始数据输入AI模型之前，通常需要进行预处理，以提高数据的质量和模型的性能。

排序: 如前所述，排序算法（如快速排序、归并排序）在数据预处理中扮演着重要角色。例如，在特征工程中，可能需要对某些特征值进行排序，以便进行后续的分析或转换。在处理时间序列数据时，确保数据按时间戳排序是基本要求。在某些模型（如决策树）的构建过程中，特征值排序是关键步骤。
去重: 去重是数据清洗的重要环节，可以避免模型因为重复数据而产生偏差或过拟合。使用集合（set）或 collections.Counter 可以高效地完成去重任务。例如，在文本数据中，去除重复的词语或句子；在用户行为数据中，去除重复的点击或购买记录。

3.2. 图算法在某些AI问题中的应用

图是一种非常强大的数据结构，能够表示实体之间的关系，在AI的许多领域都有应用。

Dijkstra 算法: Dijkstra 算法用于查找图中两个节点之间的最短路径。在AI中，它可以应用于：
- 路径规划: 例如，在自动驾驶或机器人导航中，计算从起点到终点的最优路径。
- 网络路由: 在网络通信中，寻找数据包传输的最短路径。
- 推荐系统: 寻找用户之间或物品之间的"最短关联路径"。
广度优先搜索 (BFS) 和深度优先搜索 (DFS): 这两种图遍历算法在AI中用途广泛：
- BFS: 常用于查找最短路径（在无权图中），或者在状态空间搜索中找到第一个满足条件的解。例如，在游戏AI中，可以用BFS来寻找最短的游戏步骤。在知识图谱中，可以用于查找实体之间的最短关系链。
- DFS: 常用于遍历所有可能的路径，或者在状态空间搜索中找到一个解（不一定是最近的）。例如，在解决迷宫问题、逻辑推理或某些生成模型中。
知识图谱: 知识图谱本质上是一个大规模的图，其中节点代表实体（人、地点、概念等），边代表实体之间的关系。图算法（如PageRank, 社区发现算法）在知识图谱的构建、查询和推理中发挥着核心作用，例如，用于评估实体的重要性，发现隐藏的关联，或者进行常识推理。

3.3. 搜索算法在AI决策过程中的体现

搜索算法是AI解决问题和做出决策的基础。

状态空间搜索: 许多AI问题可以被建模为在一个巨大的"状态空间"中寻找一条从初始状态到目标状态的路径。搜索算法（如BFS, DFS, A*搜索）被用来探索这个空间。
强化学习 (Reinforcement Learning): 在强化学习中，智能体（agent）通过与环境交互来学习最优策略。这个学习过程常常涉及到在"状态-动作"空间中进行搜索。例如：
- 蒙特卡洛树搜索 (Monte Carlo Tree Search, MCTS): MCTS 是一种用于决策过程的搜索算法，在围棋AI（如AlphaGo）中取得了巨大成功。它结合了随机模拟和树搜索，能够有效地评估不同行动的价值，并选择最优行动。
- 策略搜索: 智能体在学习过程中，不断搜索和优化其策略（即在给定状态下采取何种动作）。

4. NumPy 深度解析

NumPy（Numerical Python）是Python科学计算的核心库，为Python提供了强大的N维数组对象（ndarray）以及大量的数学函数。在AI领域，NumPy几乎无处不在，是进行高效数值计算的基石。

4.1. N-dimensional array (`ndarray`) 的创建、索引、切片

创建 ndarray:
- 从Python列表或元组创建：np.array([1, 2, 3]), np.array([[1, 2], [3, 4]])
- 创建特定内容的数组：
  - np.zeros((rows, cols))：创建全零数组。
  - np.ones((rows, cols))：创建全一数组。
  - np.arange(start, stop, step)：生成等差数列。
  - np.linspace(start, stop, num)：生成等间隔数列。
  - np.random.rand(rows, cols)：生成[0, 1)之间的随机数数组。
  - np.random.randn(rows, cols)：生成服从标准正态分布的随机数数组。
索引和切片: NumPy数组的索引和切片方式非常灵活，支持多维索引。
- 一维数组: arr[i] 访问第 i 个元素，arr[start:stop:step] 进行切片。
- 多维数组: arr[row, col] 访问特定行和列的元素。arr[row_slice, col_slice] 进行多维切片。
- 布尔索引 (Boolean Indexing): 使用布尔数组来选择满足条件的元素。例如，arr[arr > 0] 会选择所有大于0的元素。
- Fancy Indexing: 使用整数数组进行索引，可以实现不连续元素的选取。
  
  import numpy as np
  
  创建一个二维数组
  
  a = np.array([[1, 2, 3],
  [4, 5, 6],
  [7, 8, 9]])
  
  索引
  
  print("Element at (0, 1):", a[0, 1]) # 输出: 2
  
  切片
  
  print("First row:", a[0, :]) # 输出: [1 2 3]
  print("Second column:", a[:, 1]) # 输出: [2 5 8]
  print("Sub-array:\n", a[0:2, 1:3]) # 输出: [[2 3] [5 6]]
  
  布尔索引
  
  print("Elements greater than 5:", a[a > 5]) # 输出: [6 7 8 9]
  
  Fancy Indexing
  
  print("Elements at (0,0), (1,1), (2,2):", a[[0, 1, 2], [0, 1, 2]]) # 输出: [1 5 9]

4.2. 向量化操作 (Vectorization) 与广播 (Broadcasting) 机制

这是NumPy性能提升的关键所在。

向量化操作: 指的是对整个数组执行操作，而不需要编写显式的循环。NumPy的底层是用C语言实现的，这些操作可以直接在C层执行，速度远超Python循环。
- 例如，将一个标量加到一个数组上：arr + 5。
- 两个数组对应元素的加法：arr1 + arr2。
- 数学函数：np.sin(arr), np.exp(arr)。
广播 (Broadcasting): 是一种机制，允许NumPy在执行算术运算时，对具有不同形状的数组进行操作。NumPy会"广播"较小的数组，使其形状与较大的数组匹配，然后执行元素级运算。广播遵循以下规则：
1. 如果两个数组的维度数量不同，则将维度较少的数组的形状在前面补1，直到维度数量相同。
2. 如果两个数组在某个维度上的大小不匹配，则其中一个数组在该维度上的大小必须为1，或者两个数组在该维度上的大小必须相同。
3. 如果两个数组的形状兼容，NumPy会沿着维度大小为1的维度进行"复制"操作，使其与另一个数组的维度大小匹配。
import numpy as np

向量化操作示例

a = np.array([1, 2, 3])
b = a * 2
print("Vectorized multiplication:", b) # 输出: [2 4 6]

c = np.array([4, 5, 6])
d = a + c
print("Vectorized addition:", d) # 输出: [5 7 9]

广播示例

数组 a (3,) 和标量 10

e = a + 10
print("Broadcasting scalar:", e) # 输出: [11 12 13]

数组 a (3,) 和数组 f (3, 1)

f = np.array([[10], [20], [30]])
g = a + f
print("Broadcasting array:\n", g)

输出:

[[11 12 13]

[21 22 23]

[31 32 33]]

解释: 数组 a (3,) 被广播成 (3, 3) 的形状，数组 f (3, 1) 被广播成 (3, 3) 的形状。

向量化和广播机制极大地简化了代码，并且显著提升了计算速度，是Python进行大规模数值计算和AI模型实现效率的关键。

4.3. NumPy 的数学函数库

NumPy提供了丰富的数学函数，涵盖了线性代数、傅里叶变换、随机数生成等，为AI计算提供了强大的支持。

线性代数 (np.linalg):
- 矩阵乘法 (np.dot 或 @ 运算符)。
- 求逆 (np.linalg.inv)。
- 求特征值和特征向量 (np.linalg.eig)。
- 求解线性方程组 (np.linalg.solve)。
- 范数计算 (np.linalg.norm)。
- 这些函数在训练神经网络、进行主成分分析（PCA）等降维技术时至关重要。
通用函数 (ufuncs):
- 数学函数：np.sin, np.cos, np.exp, np.log, np.sqrt 等。
- 比较函数：np.greater, np.less, np.equal 等。
- 逻辑函数：np.logical_and, np.logical_or 等。
- 这些函数可以作用于整个数组，并支持广播。
统计函数:
- np.mean, np.median, np.std, np.var：计算均值、中位数、标准差、方差。
- np.sum, np.min, np.max：计算总和、最小值、最大值。
- 这些函数在数据分析、特征提取和模型评估中非常常用。
  
  import numpy as np
  
  线性代数示例
  
  A = np.array([[1, 2], [3, 4]])
  B = np.array([[5, 6], [7, 8]])
  
  矩阵乘法
  
  C = np.dot(A, B) # 或者 A @ B
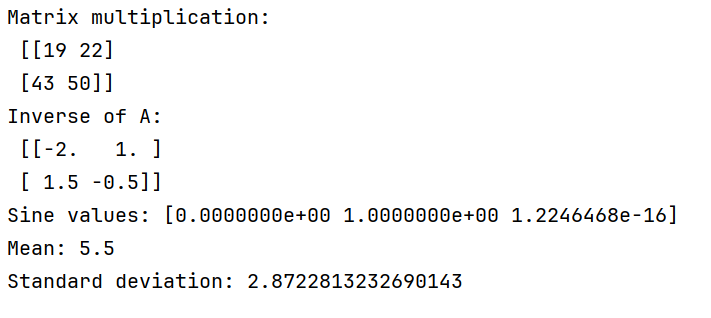
  print("Matrix multiplication:\n", C)
  
  求逆
  
  A_inv = np.linalg.inv(A)
  print("Inverse of A:\n", A_inv)
  
  通用函数示例
  
  x = np.array([0, np.pi/2, np.pi])
  print("Sine values:", np.sin(x))
  
  统计函数示例
  
  data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
  print("Mean:", np.mean(data))
  print("Standard deviation:", np.std(data))

5. 小结与AI启发

通过对Python内置数据结构、常见算法原理、以及NumPy的深入探讨，我们可以清晰地看到数据结构和算法在AI领域中的核心地位。

数据结构的选择至关重要: 一个合适的数据结构能够让数据的组织和访问变得高效。例如，在需要快速查找时，字典的 O(1) 平均查找效率远胜于列表的 O(n)；在处理大量有序数据时，利用NumPy的ndarray进行向量化操作，能够避免Python循环的开销，实现数量级的性能提升。collections模块提供的defaultdict、Counter等工具，更是为AI数据处理中的常见任务（如计数、分组）提供了简洁高效的解决方案。
算法的智慧是AI提速的关键: 无论是数据预处理中的排序和去重，还是模型训练和推理中的复杂计算，高效算法的选择和实现直接决定了AI系统的性能。理解算法的时间和空间复杂度，能够帮助我们预测其在处理大规模数据时的表现，并做出明智的优化决策。例如，选择 O(n log n) 的排序算法而非 O(n^2) 的算法，对于处理百万级数据量的预处理任务来说，是实现秒级响应的关键。图算法和搜索算法在AI的决策制定、路径规划、知识推理等方面展现出强大的能力，它们是构建智能系统的"大脑"。
NumPy是现代AI计算的基石: NumPy的ndarray提供了高效的内存管理和计算能力，其向量化操作和广播机制极大地简化了代码并提升了性能。几乎所有主流的AI框架（如TensorFlow, PyTorch）都建立在NumPy的基础之上，或者提供了与NumPy兼容的接口。因此，熟练掌握NumPy的使用，包括数组的创建、索引、切片、向量化操作以及丰富的数学函数库，是每一位AI从业者必备的技能。

总而言之，数据结构的精巧设计与算法的智慧运用，是AI系统能够高效运行、快速迭代、并在海量数据中挖掘价值的根本原因。在追求更强大AI模型的道路上，我们不能仅仅关注模型架构和训练技巧，更要深入理解并善用底层的工具------数据结构和算法。只有这样，我们才能真正释放AI的潜力，驱动其不断向前发展。

【Python进阶】数据结构的精巧与算法的智慧：AI提速的关键

1. Python内置数据结构的高级用法

1.1. list, tuple, dict, set 的性能特点与适用场景

1.2. collections 模块：AI数据处理的利器

2. 理解常见算法

2.1. 排序算法（快速排序、归并排序）的原理与Python实现

2.2. 查找算法（二分查找）的应用

2.3. 理解时间复杂度和空间复杂度

3. 算法在AI中的应用

3.1. 数据预处理中的排序、去重

3.2. 图算法在某些AI问题中的应用

3.3. 搜索算法在AI决策过程中的体现

4. NumPy 深度解析

4.1. N-dimensional array (ndarray) 的创建、索引、切片

创建一个二维数组

索引

切片

布尔索引

Fancy Indexing

4.2. 向量化操作 (Vectorization) 与广播 (Broadcasting) 机制

向量化操作示例

广播示例

数组 a (3,) 和标量 10

数组 a (3,) 和数组 f (3, 1)

输出:

[[11 12 13]

[21 22 23]

[31 32 33]]

解释: 数组 a (3,) 被广播成 (3, 3) 的形状，数组 f (3, 1) 被广播成 (3, 3) 的形状。

4.3. NumPy 的数学函数库

线性代数示例

矩阵乘法

求逆

通用函数示例

统计函数示例

5. 小结与AI启发

1.1. `list`, `tuple`, `dict`, `set` 的性能特点与适用场景

1.2. `collections` 模块：AI数据处理的利器

4.1. N-dimensional array (`ndarray`) 的创建、索引、切片