给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。

分析:
由于子数组必须是连续的,因此不能像组合问题那样随意选择元素,而是必须考虑区间。
最直接的暴力思路是:枚举每一个起点,再向右扩展终点,计算每一段区间的和,看是否等于 k。但这种做法时间复杂度是 O(n2),在数据规模较大时会超时。
比如nums=[1,2,3,4],暴力计算的时候发现会去做这些操作:
1+2
1+2+3
2+3
3+4
1+2+3+4
...
这里会发现大量的重复计算,所以我们就想,能不能想办法减少计算量?前缀和其实就是把"从 0 开始的累加"存下来,以后就别每次都重新加了,定义也就是从 0 加到当前位置的总和。
sum[0] = nums[0] =1
sum[1] = nums[0] + nums[1]=1+2
sum[2] = nums[0] + nums[1] + nums[2] =1+2+3
sum[3] = nums[0] + nums[1] + nums[2] + nums[3]=1+2+3+4
计算前缀和的时候,每次都只需要在之前算好的前缀和的基础上加上当前位置上的数就可以了。接下来就来看看前缀和和我们题目求的东西有什么联系。
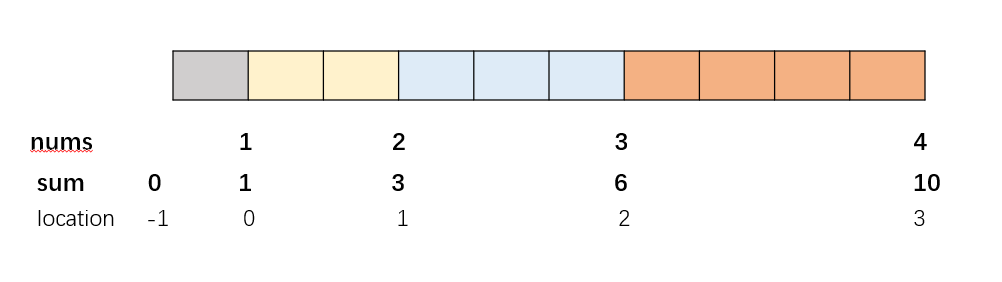
比如我们想知道2+3的和,也就是nums[1]+nums[2]的和,观察可知我们要算黄色加蓝色色块的长度,也就是sum(2)-sum(0)=6-1=5
如果我们想知道3+4的和,也就是nums[2]+nums[3]的和,观察可知我们要算蓝色加橙色色块的长度,也就是sum(3)-sum(1)=10-3=7
我们想知道任意一段子序列的和,都可以通过前缀和相减的方式得到。题目就可以翻译成有没有某个区间 [l, r],它的和等于 k?
换成前缀和来表示就是sum[r] - sum[l - 1] = k
移项得 sum[l - 1] = sum[r] - k
翻译一下就是,当我走到位置 r 时,如果在之前某个位置,前缀和等于 sum - k,那么从那个位置后面开始,到 r 的这段子数组,和就是 k。
比如刚刚的例子nums=[1,2,3,4],当我走到nums[2]=3这个位置的时候,如果要找和为5的子数组的话,就就会去看nums[2]=3之前的位置中,有没有前缀和是sum[2]-5即6-5=1的,当然有,我们找到了sum[0]=1,这时候对应location0,也就是mums[0]那个位置。但是是sum[l - 1] =1,所以这时候l-1是0,我们要找到的是l,所以要从loaction0后面的开始看,不要把nums[0]包进去,一直到nums[2]=3这个位置。最后得到的也就是这段 [l, r]是[2,3]。
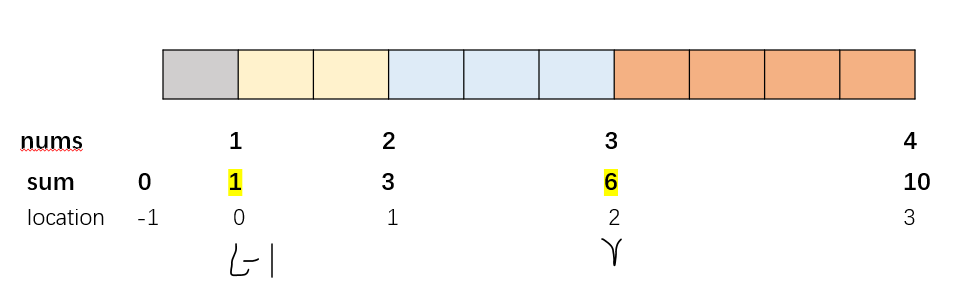
所以我们只需要从左到右一步步走,每走到一个数的时候,就去看那个位置r的前缀和sum,然后呢再去计算sum,再去看这个位置之前的前缀和有没有等于sum-k的,有的话这组[l,r]就能满足条件,和为 k 的子数组个数就可以加1了。
现在已经了解了原理,此题我们并不需要求出具体的[l,r],只需要求出和为k的子数组的个数就行了。现在的解法是,每走到一个新位置,都要问一次:sum - k 有没有出现过,然后统计下次数,自然想到:我是不是应该把"出现过的值"存起来?否则每次都要回头从头查一遍。我们目前需要能快速判断某个数是否出现过,还能知道它出现过几次,这种形式最适合用哈希表。
定义一个变量 sum 表示当前遍历到的位置为止的前缀和,同时使用一个哈希表 mp 来记录之前出现过的前缀和以及它们出现的次数。也就是说,哈希表中的每一项含义都是:
- mp[某个前缀和] = 该前缀和出现过的次数
比如mp[2] = 3就代表前缀和等于2出现过3次。
在正式开始遍历数组之前,需要先对哈希表进行一次初始化,人为规定将 mp[0] = 1。这一点非常关键,它表示在还没有遍历任何元素之前,前缀和为 0 的情况已经出现过一次。这样做的目的,是为了能够正确统计从数组下标 0 开始、其和恰好等于 k 的子数组,否则这类情况会被漏掉。例如,当 nums = [1, 2, 3],k = 3 时,子数组 [1, 2] 本身就满足条件,这时候sum-k=3-3=0,这时候该去找前缀和为0的记录有没有,如果不提前记录前缀和为 0 的情况,这一答案就会被漏掉。
随后,从左到右遍历数组中的每一个元素。每走到一个新位置,首先将当前元素累加到 sum 中,表示更新到当前位置为止的前缀和。接着,就可以利用哈希表来判断是否存在满足条件的子数组。
如果在哈希表中发现 sum - k 这个值,说明在当前位置之前,曾经有若干个位置的前缀和等于 sum - k。根据前缀和的定义,这些位置之后到当前位置所形成的子数组,其元素之和正好等于 k。因此,此时需要将 mp[sum - k] 的值累加到答案中,而不是简单地加 1,因为同一个前缀和可能在不同位置出现多次,对应着多个不同的合法子数组。例如,考虑数组 nums = [1, 2, 0, 3],k = 3。当遍历到元素 3 时,当前的前缀和为 sum = 6,此时我们会去查找 sum - k = 3。而在之前的遍历过程中,前缀和 3 曾经出现过两次(对应 [1,2] 和 [1,2,0])。这意味着存在两段不同的子数组,它们都以当前元素结尾,并且和为 3,分别是 [0,3] 和 [3]。因此在这种情况下,答案需要增加 2,而不是只增加 1。注意每次完成统计之后,还需要将当前的前缀和 sum 记录到哈希表中,存起来给未来用。
整个遍历过程中始终遵循一个顺序:先利用已有的哈希表统计答案,再将当前前缀和加入哈希表。这样可以避免把当前位置本身错误地当作子数组的起点,从而保证统计结果的正确性。
最终,当数组遍历结束时,累加得到的计数结果即为数组中和为 k 的子数组个数。
用这个例子来完整走一遍算法,用res来记录满足条件的子数组个数:
nums = [1, 2, 0, 3]
k = 3
遍历数组前:
sum = 0
res = 0
mp = { 0 : 1 }
这里的含义是:
- sum = 0:当前还没有加任何元素
- res = 0:还没有找到任何子数组
- mp[0] = 1:表示在数组开始之前,有一个前缀和是 0,这个是人为规定的
第 1 步:遍历到 nums[0] = 1
更新前缀和sum = 0 + 1 = 1,表示从开始到当前位置 0的这段[1],元素之和是 1。
判断是否存在一个位置,其前缀和 = sum - k = 1 - 3 = -2
查看哈希表:mp 中没有 -2,说明当前位置之前,不存在某个位置能够和当前位置一起组成和为 3 的子数组
res 不变,记录当前前缀和到哈希表中,说明前缀和为 1 的位置,现在出现了一次
此时:sum = 1,res = 0,mp = {0:1, 1:1}
第 2 步:遍历到 nums[1] = 2
更新前缀和 sum = 1 + 2 = 3,表示从开始到当前位置 1 的这段 [1,2],元素之和是 3。
判断是否存在一个位置,其前缀和 = sum - k = 3 - 3 = 0。
查看哈希表:mp[0] = 1,说明从下标 -1 之后到当前位置 1,可以组成和为 3 的子数组 [1,2] 。
res = 0 + 1 = 1,记录当前前缀和到哈希表中,说明前缀和为 3 的位置,现在出现了一次。
此时:sum = 3,res = 1,mp = {0:1, 1:1, 3:1}
第 3 步:遍历到 nums[2] = 0
更新前缀和 sum = 3 + 0 = 3,表示从 -1 处到当前位置 2 的这段 [1,2,0],元素之和仍然是 3。
判断是否存在一个位置,其前缀和 = sum - k = 3 - 3 = 0。
查看哈希表:mp[0] = 1,说明从数组开始到当前位置 2,可以组成和为 3 的子数组 [1,2,0] 。
res = 1 + 1 = 2,记录当前前缀和到哈希表中,说明前缀和为 3 的位置,又出现了一次。
此时:sum = 3,res = 2,mp = {0:1, 1:1, 3:2}
第 4 步:遍历到 nums[3] = 3
更新前缀和 sum = 3 + 3 = 6,表示从 -1 处到当前位置 3 的这段 [1,2,0,3],元素之和是 6。
判断是否存在一个位置,其前缀和 = sum - k = 6 - 3 = 3。
查看哈希表:mp[3] = 2,说明之前有两个位置前缀和为 3,从这两个位置之后到当前位置 3,都可以组成和为 3 的子数组,对应 [0,3] 和 [3] 。
res = 2 + 2 = 4,记录当前前缀和到哈希表中,说明前缀和为 6 的位置,现在出现了一次。
此时:sum = 6,res = 4,mp = {0:1, 1:1, 3:2, 6:1}
最终结果:res = 4,对应的子数组是[1,2]、[1,2,0]、[0,3]、[3]
C++代码如下:
cpp
#include<iostream>
#include<vector>
#include<unordered_map>
using namespace std;
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> mp;// mp 用来记录:某个前缀和出现了多少次
int res = 0;// 满足条件的子数组个数
int sum = 0;// 当前前缀和
mp[0] = 1;// 初始一个虚拟位置,表示前缀和为0出现了一次
for (int i = 0; i < nums.size(); i++) {
sum = sum + nums[i];// 更新当前位置的前缀和
if (mp.count(sum - k)) {// 查找是否存在前缀和 = sum - k
res = res + mp[sum - k];
}
mp[sum]++;// 把当前前缀和记录进哈希表
}
return res;
}
};