Robust Clutter Rejection in Passive Radar via Generalized Subband Cancellation

摘要------被动雷达（Passive radar）常因高杂波干扰而受到影响。在本文中，提出了一种广义子带取消（generalized subband cancellation，GSC）算法，以实现稳健的杂波抑制。

该算法充分考虑了四个主要影响因素，即载波频率偏移 、采样频率偏移 、分数延迟 以及硬件频率响应 。 GSC \text{GSC} GSC 算法利用子带信号处理和定制的杂波子空间构建，来解决由这些因素引起的问题。

定量评估表明， GSC \text{GSC} GSC 算法接近最优的杂波消除性能。其有效性也通过野外实验数据得到了验证。

文章目录

• • [I. INTRODUCTION](#I. INTRODUCTION)
  • [II. SIGNAL MODEL](#II. SIGNAL MODEL)
  • • [A. Conventional Signal Model](#A. Conventional Signal Model)
    • [B. Signal Model With Nonideal Factors](#B. Signal Model With Nonideal Factors)
  • [III. GENERALIZED SUBBAND CANCELLATION](#III. GENERALIZED SUBBAND CANCELLATION)
  • • [A. 算法描述](#A. 算法描述)

I. INTRODUCTION

被动雷达，也称为被动相干定位，利用第三方广播源作为机会照亮源（illuminators of
opportunity，IOs），以探测感兴趣目标的反射信号。由于不需要部署专用发射机，被动雷达可以隐蔽工作。这一特性引起了学术界和工业界的极大兴趣 [1]--[3]。

最广泛考虑的 IOs 是地面电视和广播 [4]--[9]。这些 IOs 连续发射信号。除了目标回波外，被动雷达还会接收到直达径信号和强地面杂波。由于信号并非为雷达应用而设计，即使目标回波在距离-多普勒（RD）图上与之分离，也会被直达径信号和地面杂波的旁瓣所淹没。直达径信号和地面杂波由于对目标探测的影响非常相似，通常统称为杂波。杂波抑制是被动雷达信号处理中的关键步骤。

被动雷达中的杂波抑制方法大致可分为两类：空间方法 和时间方法。

• 空间方法 [10]--[14] 使用自适应波束形成，通过在杂波方向或多个杂波的复合子空间中形成零陷来消除杂波。当被动雷达仅配备单个接收通道或少量接收通道时，空间方法的性能通常不尽如人意。在本文中，我们重点关注时间方法。

• 时间杂波抑制（temporal clutter rejection）也称为杂波消除（clutter cancellation），因为其移除操作是基于减法的。

  • 经典的杂波消除方法包括自适应滤波器，例如 最小均方（LMS）滤波器、归一化 LMS 滤波器、递归最小二乘滤波器、梯度自适应晶格滤波器（gradient adaptive lattice filter）等 [15]--[17]。监视信号和参考信号是这些自适应滤波器的输入。通过从监视信号中减去参考信号与自适应更新系数的卷积，监视信号中的杂波大部分可以被移除。

  • 另一种广泛使用的杂波消除方法是扩展消除算法（ECA）及其分批版本（ ECA-B）[18]。此外还有一些 ECA 的改进版本，例如 ECA on subcarrier [19], [20] 以及 sliding ECA [21]。ECA 的基本思想是根据最小二乘（LS）准则，从监视信号中减去经过延迟和适当加权的参考信号副本。这一过程是通过将监视信号沿参考信号构建的杂波子空间进行正交投影来实现的。

上述杂波消除方法中存在一个共同的潜在假设（a common underlying assumption），即监视信号中的杂波是参考信号经过延迟和适当加权的副本。然而，这在实际中可能并不充分。

• 以数字地面电视和广播的 IOs 为例（Taking the IOs of digital terrestrial television and broadcasting as an example），由于发射机和接收机中的振荡器和时钟不同源，接收信号中存在 载波频率偏移（CFO） 和 采样频率偏移（SFO）。上述提到的潜在假设将偏离实际情况，从而导致杂波消除性能显著下降。
• 此外（Besides），杂波的延迟可能不是采样周期的整数倍（not be an integer multiple of the sampling period）。我们称之为分数延迟（fractional delay）。对于离散信号而言，这会给杂波消除带来麻烦。
• 此外（Moreover），发射机和接收机的硬件频率响应（the hardware frequency response）是另一个需要关注（which needs to be paid attention to）的非理想因素。

为了解决由这些非理想因素引起的问题，我们在本文中提出了一种 广义子带取消（generalized subband cancellation，GSC）算法。GSC 算法

• 首先借助近似等效和子带信号处理，将四个非理想因素统一为两个非理想因素。
• 随后，这两个非理想因素通过定制化杂波子空间构建的方法得以解决。所构建的杂波子空间准则是通过解析推导建立的（is established analytically）。
• 消除性能还利用模拟数据和 field experimental data 进行了定量评估。

本文其余部分的结构安排如下。第二节描述了信号模型并建立了杂波抑制性能指标。第三节介绍了所提出的 GSC 方法。第四节通过数值模拟和实验数据处理展示了杂波消除性能。最后，在第五节中给出了结论。

II. SIGNAL MODEL

在本节中，首先给出常规信号模型。然后，我们建立一个考虑了四个主要非理想因素的信号模型。此外，我们提出了一个指标，用于定量评估杂波抑制性能（quantitatively evaluate the clutter rejection performance）。

A. Conventional Signal Model

假设地面杂波可以表示为多个静止点散射体的集合。在发射机和接收机静止的情况下，杂波通常具有零多普勒频率，而运动目标的反射回波则具有非零多普勒频率。

对于双基对（即一对发射机-接收机），监视信道的基带信号由下式给出：

s surv ′ ( t ) = c 1 d ( t ) + ∑ m = 2 M c c m d ( t − τ m c ) + ∑ p = 1 P α p d ( t − τ p ) e j 2 π f D , p t + g surv ( t ) (1) s'{\text{surv}}(t) = c_1 d(t) + \sum{m=2}^{M_c} c_m d(t - \tau_m^c) + \sum_{p=1}^P \alpha_p d(t - \tau_p) e^{j2\pi f_{D,p} t} + g_{\text{surv}}(t) \tag{1} ssurv′(t)=c1d(t)+m=2∑Mccmd(t−τmc)+p=1∑Pαpd(t−τp)ej2πfD,pt+gsurv(t)(1)

• 其中 d ( t ) d(t) d(t) 是直达径信号， c 1 c_1 c1 是相应的复振幅。
• c m c_m cm 和 τ m c \tau_m^c τmc 分别是第 m m m 个静止散射分量（ m = 2 , ... , M c m = 2, \dots, M_c m=2,...,Mc）的复振幅和相对于直达径的延迟。
• α p \alpha_p αp、 τ p \tau_p τp 和 f D , p f_{D,p} fD,p 分别是第 p 个目标（ p = 1 , ... , P p = 1, \dots, P p=1,...,P）的复振幅、延迟和多普勒频率。
• g surv ( t ) g_{\text{surv}}(t) gsurv(t) 是加性高斯白噪声。

为了叙述简练（For description brevity），在下文（in the following text）中我们将直达径分量和静止散射分量统称为杂波，而不作区分。

同样地（Likewise），参考信道的基带信号由下式给出：

s ref ′ ( t ) = c 1 ′ d ( t ) + ∑ m = 2 M c ′ c m ′ d ( t − τ ~ m c ) + g ref ( t ) (2) s'_{\text{ref}}(t) = c'1 d(t) + \sum{m=2}^{M'_c} c'_m d(t - \tilde{\tau}m^c) + g{\text{ref}}(t) \tag{2} sref′(t)=c1′d(t)+m=2∑Mc′cm′d(t−τ~mc)+gref(t)(2)

其中 c 1 ′ c'_1 c1′、 c m ′ c'm cm′、 τ ~ m c \tilde{\tau}m^c τ~mc 和 g ref ( t ) g{\text{ref}}(t) gref(t) 的定义与 c 1 c_1 c1、 c m c_m cm、 τ m c \tau_m^c τmc 和 g surv ( t ) g{\text{surv}}(t) gsurv(t) 的定义相似。由于参考信道通常指向发射机，因此在式 (2) 中忽略了目标回波。

当考虑单频网（single frequency network，SFN）时，SFN 中的所有发射机同时以相同的频率发射相同的信号。假设 SFN 中有 N t N_t Nt 个发射机，信号模型由下式给出：

s surv ′ ( t ) = ∑ n = 1 N t c n , 1 d ( t − t n ) + ∑ n = 1 N t ∑ m = 2 M c c n , m d ( t − τ n , m c ) + ∑ n = 1 N t ∑ p = 1 P α n , p d ( t − τ n , p ) e j 2 π f D , n , p t + g surv ( t ) (3) s'{\text{surv}}(t) = \sum{n=1}^{N_t} c_{n,1} d(t - t_n) + \sum_{n=1}^{N_t} \sum_{m=2}^{M_c} c_{n,m} d(t - \tau_{n,m}^c) + \sum_{n=1}^{N_t} \sum_{p=1}^P \alpha_{n,p} d(t - \tau_{n,p}) e^{j2\pi f_{D,n,p} t} + g_{\text{surv}}(t) \tag{3} ssurv′(t)=n=1∑Ntcn,1d(t−tn)+n=1∑Ntm=2∑Mccn,md(t−τn,mc)+n=1∑Ntp=1∑Pαn,pd(t−τn,p)ej2πfD,n,pt+gsurv(t)(3) s ref ′ ( t ) = ∑ n = 1 N t c n , 1 ′ d ( t − t n ) + ∑ n = 1 N t ∑ m = 2 M c ′ c n , m ′ d ( t − τ ~ n , m c ) + g ref ( t ) (4) s'{\text{ref}}(t) = \sum{n=1}^{N_t} c'{n,1} d(t - t_n) + \sum{n=1}^{N_t} \sum_{m=2}^{M'c} c'{n,m} d(t - \tilde{\tau}{n,m}^c) + g{\text{ref}}(t) \tag{4} sref′(t)=n=1∑Ntcn,1′d(t−tn)+n=1∑Ntm=2∑Mc′cn,m′d(t−τ~n,mc)+gref(t)(4)

其中 d ( t − t n ) d(t - t_n) d(t−tn) 是第 n 个发射机的直达径信号。在不失一般性的情况下（Without loss of generality），我们假设第一个发射机是最近的一个，且 t 1 = 0 t_1 = 0 t1=0。其他延迟是相对于第一个直达径信号的。在式 (3) 和 (4) 的信号模型中，假设监视信道和参考信道是同址部署的。

在单频网（SFN）环境下，存在多个发射机（ N t N_t Nt 个）。由于两个接收通道位于同一地点，它们接收到来自同一个发射机 n n n 的直达径信号的时间延迟 t n t_n tn 是相同的。

B. Signal Model With Nonideal Factors

上述信号表示是不考虑实际系统影响的理想信号模型。在本节中，我们建立了一个更真实的信号模型，其中考虑了四个主要的非理想因素。这些非理想因素分别是 CFO、SFO、分数延迟（fractional delay）和硬件频率响应（hardware frequency response）。所有这些因素都可能对杂波抑制（clutter rejection）产生重大影响。

在实际系统中，接收端和发射端的振荡器是不同的。它们之间的频率偏移称为 CFO。关于 SFN，虽然所有发射机名义上都工作在相同的频率上，但各载波频率之间存在差异。事实上，无线广播和电视标准允许一定水平的 CFO。特别是在数字电视地面多媒体广播（digital television terrestrial multimedia broadcasting）中，允许的 CFO 水平为 1 Hz [22]，而在地面数字视频广播（digital video broadcasting-terrestrial）中的值为子载波频率间隔的 1/1000 [23]。因此，SFN 中的每个发射机都可能具有独立的 CFO。令 f CFO , n f_{\text{CFO},n} fCFO,n 表示对应于第 n 个发射机的 CFO。信号模型 (3) 和 (4) 变为如下形式：

s surv ′ ( t ) = ∑ n = 1 N t c n , 1 d ( t − t n ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ m = 2 M c c n , m d ( t − τ n , m c ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ p = 1 P α n , p d ( t − τ n , p ) e j 2 π f D , n , p t e j 2 π f CFO , n t + g surv ( t ) (5) s'{\text{surv}}(t) = \sum{n=1}^{N_t} c_{n,1} d(t - t_n) e^{j2\pi f_{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{m=2}^{M_c} c_{n,m} d(t - \tau_{n,m}^c) e^{j2\pi f_{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{p=1}^P \alpha_{n,p} d(t - \tau_{n,p}) e^{j2\pi f_{D,n,p} t} e^{j2\pi f_{\text{CFO},n} t} + g_{\text{surv}}(t) \tag{5} ssurv′(t)=n=1∑Ntcn,1d(t−tn)ej2πfCFO,nt+n=1∑Ntm=2∑Mccn,md(t−τn,mc)ej2πfCFO,nt+n=1∑Ntp=1∑Pαn,pd(t−τn,p)ej2πfD,n,ptej2πfCFO,nt+gsurv(t)(5) s ref ′ ( t ) = ∑ n = 1 N t c n , 1 ′ d ( t − t n ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ m = 2 M c ′ c n , m ′ d ( t − τ ~ n , m c ) e j 2 π f CFO , n t + g ref ( t ) (6) s'{\text{ref}}(t) = \sum{n=1}^{N_t} c'{n,1} d(t - t_n) e^{j2\pi f{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{m=2}^{M'c} c'{n,m} d(t - \tilde{\tau}{n,m}^c) e^{j2\pi f{\text{CFO},n} t} + g_{\text{ref}}(t) \tag{6} sref′(t)=n=1∑Ntcn,1′d(t−tn)ej2πfCFO,nt+n=1∑Ntm=2∑Mc′cn,m′d(t−τ~n,mc)ej2πfCFO,nt+gref(t)(6)

SFO 被定义为实际采样频率与标称采样频率之间的频率偏移（frequency offset between the

actual sampling frequency and the nominal sampling frequency）。它是由发射机中模数转换器和接收机中数模转换器的时钟偏差引起的。当参考信号通过重构获得时，SFO 非常重要。其影响将在参考信号重构描述之后进行讨论。

分数延迟（Fractional delay）会给数字信号处理带来麻烦。令 f s f_s fs 和 T s T_s Ts 分别表示实际采样频率和采样周期。令 d [ n ] ≜ d ( n T s ) d[n] \triangleq d(n T_s) d[n]≜d(nTs) 表示发射信号的离散序列。一个重要的问题是如何使用 d [ n ] d[n] d[n] 来表示杂波分量 c d ( n T s − τ ) c d(n T_s - \tau) cd(nTs−τ)。

• 情况 1 杂波延迟 τ \tau τ 是采样周期 T s T_s Ts 的整数倍，即 τ = n c T s \tau = n_c T_s τ=ncTs，其中 n c n_c nc 是一个整数。我们称这种情况为整数延迟。我们有以下关系：
  c d ( n T s − τ ) = c d ( n T s − n c T s ) = c d [ n − n c ] (7) cd(n T_s - \tau) = cd(n T_s - n_c T_s) = cd[n - n_c] \tag{7} cd(nTs−τ)=cd(nTs−ncTs)=cd[n−nc](7) c d ( n T s − τ ) cd(n T_s - \tau) cd(nTs−τ) 是 d [ n ] d[n] d[n] 的时间平移版本。

• 情况 2 杂波延迟 τ \tau τ 不是采样周期 T s T_s Ts 的整数倍，即 τ = n c T s + α T s , 0 < α < 1 \tau = n_c T_s + \alpha T_s, 0 < \alpha < 1 τ=ncTs+αTs,0<α<1。这被称为分数延迟。在这种情况下， c d ( n T s − τ ) cd(n T_s - \tau) cd(nTs−τ) 无法通过平移 d [ n ] d[n] d[n] 获得。另一种替代表示方法参考了从离散信号恢复模拟信号的过程。即： c d ( n T s − τ ) = c ∑ m = − ∞ ∞ d [ m − n c ] sin ⁡ [ π ( n − m − α ) ] π ( n − m − α ) (8) cd(n T_s - \tau) = c \sum_{m=-\infty}^{\infty} d[m - n_c] \frac{\sin [\pi(n - m - \alpha)]}{\pi(n - m - \alpha)} \tag{8} cd(nTs−τ)=cm=−∞∑∞d[m−nc]π(n−m−α)sin[π(n−m−α)](8)现在 c d ( n T s − τ ) cd(n T_s - \tau) cd(nTs−τ) 被表示为平移后的 d [ n ] d[n] d[n] 的加权和。这比情况 1 更复杂。

此外，硬件的频率响应也应体现在信号模型中。假设硬件工作在线性区域。令 H ( f ) H(f) H(f) 为硬件频率响应。考虑硬件频率响应后，任意信号 s ( t ) s(t) s(t) 的频谱变为如下形式：

S FR ( f ) = H ( f ) S ( f ) (9) S_{\text{FR}}(f) = H(f) S(f) \tag{9} SFR(f)=H(f)S(f)(9)

式 (9) 的时域表达式如下：

s FR ( t ) = h ( t ) ⊗ s ( t ) (10) s_{\text{FR}}(t) = h(t) \otimes s(t) \tag{10} sFR(t)=h(t)⊗s(t)(10)

其中 s FR ( t ) s_{\text{FR}}(t) sFR(t) 和 h ( t ) h(t) h(t) 分别表示 S FR ( f ) S_{\text{FR}}(f) SFR(f) 和 H ( f ) H(f) H(f) 的时域表达式。" ⊗ \otimes ⊗" 表示卷积。因此，硬件频率响应相当于在物理信道之外引入了额外的信道响应。一方面，它导致了等效信道长度的延伸。此外，由于 h ( t ) h(t) h(t) 是连续时间函数，它还会引入分数延迟。

考虑到所有四个非理想因素，信号模型可以表示如下：

s surv ′ ′ ( t ) = h surv ( t ) ⊗ { ∑ n = 1 N t c n , 1 d ( t − t n ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ m = 2 M c c n , m d ( t − τ n , m c ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ p = 1 P α n , p d ( t − τ n , p ) e j 2 π f D , n , p t e j 2 π f CFO , n t } + g surv ( t ) (11) s''{\text{surv}}(t) = h{\text{surv}}(t) \otimes \left\{ \sum_{n=1}^{N_t} c_{n,1} d(t - t_n) e^{j2\pi f_{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{m=2}^{M_c} c_{n,m} d(t - \tau_{n,m}^c) e^{j2\pi f_{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{p=1}^P \alpha_{n,p} d(t - \tau_{n,p}) e^{j2\pi f_{D,n,p} t} e^{j2\pi f_{\text{CFO},n} t} \right\} + g_{\text{surv}}(t) \tag{11} ssurv′′(t)=hsurv(t)⊗{n=1∑Ntcn,1d(t−tn)ej2πfCFO,nt+n=1∑Ntm=2∑Mccn,md(t−τn,mc)ej2πfCFO,nt+n=1∑Ntp=1∑Pαn,pd(t−τn,p)ej2πfD,n,ptej2πfCFO,nt}+gsurv(t)(11)

s ref ′ ′ ( t ) = h ref ( t ) ⊗ [ ∑ n = 1 N t c n , 1 ′ d ( t − t n ) e j 2 π f CFO , n t + ∑ n = 1 N t ∑ m = 1 M c ′ c n , m ′ d ( t − τ ~ n , m c ) e j 2 π f CFO , n t ] + g ref ( t ) (12) s''{\text{ref}}(t) = h{\text{ref}}(t) \otimes \left[ \sum_{n=1}^{N_t} c'{n,1} d(t - t_n) e^{j2\pi f{\text{CFO},n} t} + \sum_{n=1}^{N_t} \sum_{m=1}^{M'c} c'{n,m} d(t - \tilde{\tau}{n,m}^c) e^{j2\pi f{\text{CFO},n} t} \right] + g_{\text{ref}}(t) \tag{12} sref′′(t)=href(t)⊗ n=1∑Ntcn,1′d(t−tn)ej2πfCFO,nt+n=1∑Ntm=1∑Mc′cn,m′d(t−τ~n,mc)ej2πfCFO,nt +gref(t)(12)

其中 h surv ( t ) h_{\text{surv}}(t) hsurv(t) 和 h ref ( t ) h_{\text{ref}}(t) href(t) 分别是监视信道和参考信道的时域冲激响应。采样后的信号模型由下式给出：

s surv ′ ′ [ n ] = s surv ′ ′ ( n T s ) (13) s''{\text{surv}}[n] = s''{\text{surv}}(n T_s) \tag{13} ssurv′′[n]=ssurv′′(nTs)(13)

s ref ′ ′ [ n ] = s ref ′ ′ ( n T s ) (14) s''{\text{ref}}[n] = s''{\text{ref}}(n T_s) \tag{14} sref′′[n]=sref′′(nTs)(14)

由于参考信号中的接收信号受到多径和噪声的污染，通常会执行纯化操作以获得更干净的发射信号（称为参考信号）。该参考信号随后被用作时域杂波消除中的参考样本，以及互模糊函数（CAF）计算中的匹配样本。对于数字电视和广播，一种广泛使用的纯化方法（purification approach）是重构参考信号 [24]--[26]。本文采用了该方法。

在参考信号重构中，首先在重构过程中估计 CFO，并在参考信道和监视信道中都进行补偿。即：

s surv [ n ] = s surv ′ ′ ( n T s ) e − j 2 π f ^ CFO n T s _ NV (15) s_{\text{surv}}[n] = s''{\text{surv}}(n T_s) e^{-j2\pi \hat{f}{\text{CFO}} n T_{s\_\text{NV}}} \tag{15} ssurv[n]=ssurv′′(nTs)e−j2πf^CFOnTs_NV(15)

s ref ′ ′ ′ [ n ] = s ref ′ ′ ( n T s ) e − j 2 π f ^ CFO n T s _ NV (16) s'''{\text{ref}}[n] = s''{\text{ref}}(n T_s) e^{-j2\pi \hat{f}{\text{CFO}} n T{s\_\text{NV}}} \tag{16} sref′′′[n]=sref′′(nTs)e−j2πf^CFOnTs_NV(16)

其中 f ^ CFO \hat{f}{\text{CFO}} f^CFO 表示估计的 CFO。 T s _ NV T{s\\text{NV}} Ts_NV（或 f s _ NV f{s\\text{NV}} fs_NV）表示标称采样周期（nominal sampling period，或频率）。当实际采样频率不精确可知时，使用 T s _ NV T{s\\text{NV}} Ts_NV。模型 (15) 是监视信号的最终模型。应当注意，存在残留 CFO。 s ref ′ ′ ′ [ n ] s'''{\text{ref}}[n] sref′′′[n] 中的残留 CFO 将在重构过程中通过信道估计、解码和纠错得到进一步缓解。此外，得益于硬件的发展，SFO 通常很小。重构对这种微小的 SFO 具有稳健性。这意味着误码率处于一定范围内。

经过解码和纠错后，根据调制标准对参考信号进行数字再生。当我们将参考信号表示为 d ( t ) d(t) d(t) 形式时，应在此处使用标称采样频率。总而言之，重构后的参考信号由直达信号和噪声组成。其表达式如下：

s ref [ n ] = d ( n T s _ NV ) + g ref [ n ] (17) s_{\text{ref}}[n] = d(n T_{s\\text{NV}}) + g{\text{ref}}[n] \tag{17} sref[n]=d(nTs_NV)+gref[n](17)

其中 g ref [ n ] g_{\text{ref}}[n] gref[n] 表示由重构中的比特错误引入的噪声。

对比 (15) 与 (17)，SFO 便显现出来。令 d NV [ n ] ≜ d ( n T s _ NV ) d_{\text{NV}}[n] \triangleq d(n T_{s\\text{NV}}) dNV[n]≜d(nTs_NV) 且 T s = κ T s _ NV T_s = \kappa T{s\_\text{NV}} Ts=κTs_NV。如果我们忽略信号处理中的 SFO，则对应于 d [ n ] d[n] d[n] 的等效连续信号变为 d ( κ t ) d(\kappa t) d(κt)。令 D ( f ) D(f) D(f) 为 d ( t ) d(t) d(t) 的频谱。 d ( κ t ) d(\kappa t) d(κt) 的频谱可以表示如下：

F [ d ( κ t ) ] = 1 ∣ κ ∣ D ( f κ ) (18) \mathcal{F}[d(\kappa t)] = \frac{1}{|\kappa|} D \left( \frac{f}{\kappa} \right) \tag{18} F[d(κt)]=∣κ∣1D(κf)(18)

其中 " F \mathcal{F} F" 是傅里叶变换算子。因此，忽略 SFO 会导致频谱扩展（ κ < 1 \kappa < 1 κ<1）或压缩（ κ > 1 \kappa > 1 κ>1）。这种效应应在杂波抑制中予以考虑。

参考信号是"数字重构"的（极其标准），而监视信号是"硬件采样"的（有偏差），两者之间存在的 SFO 会导致信号频谱发生形变。

III. GENERALIZED SUBBAND CANCELLATION

在本节中，我们提出了一种考虑了上述非理想因素的广义子带消除算法。首先对算法进行描述，随后讨论作为该算法关键步骤的杂波子空间构建准则。此外，还对计算复杂度进行了分析。

A. 算法描述

我们将子带信号处理（subband signal processing）引入杂波抑制中，以解决由 SFO 和分数延迟引起的问题。

• 子带信号处理是声学回声消除应用中广为人知的工具 [28]。
• 最近，有研究 [29] 利用它来提高 LMS 滤波器的收敛性能。
• 另一项试验表明，用于杂波消除的子带自适应滤波可能对硬件频率响应具有稳健性。

硬件频率响应可能导致等效通道长度的延伸（the extension of the equivalent channel length）和分数延迟。等效通道长度的延伸可以通过增加滤波器阶数轻松解决。因此，硬件频率响应的影响主要体现在分数延迟问题（fractional delay）上。

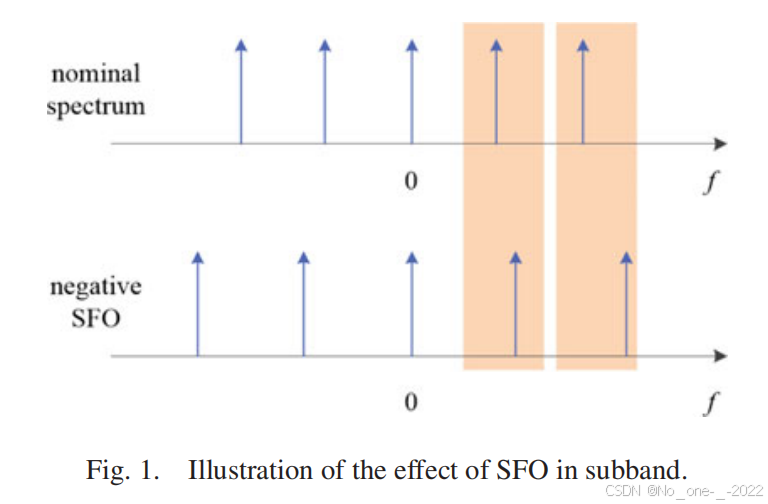
关于 SFO，它会导致频谱扩展或压缩。当进行子带信号处理时，对于 SFO 的影响存在一种近似等效性。如图 1 所示，每个子带在频谱中用一个箭头表示。上图表示标称采样频率下的频谱，下图显示了具有负 SFO 的频谱。当我们将注意力集中在一个子带时，SFO 的影响主要表现为平移，类似于 CFO。特别是当子带足够窄时，子带的扩展或压缩是可以忽略不计的。那么在子带信号处理中，SFO 可以高精度地等效为 CFO。

当我们利用子带信号处理并进一步考虑 CFO 和分数延迟时，所有上述提到的四个非理想因素都可以得到解决。这是所提出的 GSC 算法的关键点。

GSC 算法的框图如图 2 所示。首先，我们利用参考信号构建一个杂波子空间。然后，我们将监视信号和杂波子空间转换到子带域。在每个子带中执行 LS 自适应滤波，这可以去除监视信号中的杂波。最后，利用所有子带合成滤波后的监视信号。输出为时域中滤波后的监视信号。

具体而言，首先定义增强参考信号向量如下：

s ref ′ = [ s ref [ − n R + 1 ] , ... , s ref [ 0 ] , s ref [ 1 ] , ... , s ref [ N − 1 ] ] T (27) \boldsymbol{s}{\text{ref}}' = [s{\text{ref}}[-n_R + 1], \dots, s_{\text{ref}}[0], s_{\text{ref}}[1], \dots, s_{\text{ref}}[N - 1]]^T \tag{27} sref′=[sref[−nR+1],...,sref[0],sref[1],...,sref[N−1]]T(27)

杂波子空间构建由 CFO 杂波子空间和延迟杂波子空间组成。CFO 杂波子空间的构建考虑了可能的 CFO。此步骤的输出符合以下形式：

S ref ′ = [ Λ f 1 s ref ′ , ... , Λ f Q s ref ′ ] (28) \boldsymbol{S}{\text{ref}}' = [\boldsymbol{\Lambda}{f_1} \boldsymbol{s}{\text{ref}}', \dots, \boldsymbol{\Lambda}{f_Q} \boldsymbol{s}_{\text{ref}}'] \tag{28} Sref′=[Λf1sref′,...,ΛfQsref′](28)

其中

Λ f = diag { 1 , e j 2 π f T s , ... , e j 2 π f ( N + n R − 1 ) T s } (29) \boldsymbol{\Lambda}_f = \text{diag} \{1, e^{j2\pi f T_s}, \dots, e^{j2\pi f(N + n_R - 1) T_s}\} \tag{29} Λf=diag{1,ej2πfTs,...,ej2πf(N+nR−1)Ts}(29)

且 f 1 , ... , f Q f_1, \dots, f_Q f1,...,fQ 是选定的频率。

延迟杂波子空间构建考虑了可能的杂波延迟。随后，构建的杂波子空间表示如下：

S c = B [ D n 1 S ref ′ , ... , D n R S ref ′ ] (30) \boldsymbol{S}c = \boldsymbol{B} [\boldsymbol{D}^{n_1} \boldsymbol{S}{\text{ref}}', \dots, \boldsymbol{D}^{n_R} \boldsymbol{S}_{\text{ref}}'] \tag{30} Sc=B[Dn1Sref′,...,DnRSref′](30)

其中 τ 1 = n 1 T s , ... , τ R = n R T s \tau_1 = n_1 T_s, \dots, \tau_R = n_R T_s τ1=n1Ts,...,τR=nRTs 是选定的延迟。 n 1 n_1 n1 通常等于零。D 是单步移位矩阵，定义如下：

D = { d i j } i , j = 1 , ... , N + n R − 1 , d i j = { 1 , i = j + 1 0 , 其他 (31) \boldsymbol{D} = \{d_{ij}\}{i,j=1,\dots,N+n_R-1}, d{ij} = \begin{cases} 1, & i = j + 1 \\ 0, & \text{其他} \end{cases} \tag{31} D={dij}i,j=1,...,N+nR−1,dij={1,0,i=j+1其他(31)

B 是一个关联矩阵，它仅选择其右侧矩阵的最后 N 行，定义如下：

B = { b i j } i = 1 , ... , N , j = 1 , ... , N + n R − 1 , b i j = { 1 , i = j − n R + 1 0 , 其他 (32) \boldsymbol{B} = \{b_{ij}\}{i=1,\dots,N,j=1,\dots,N+n_R-1}, b{ij} = \begin{cases} 1, & i = j - n_R + 1 \\ 0, & \text{其他} \end{cases} \tag{32} B={bij}i=1,...,N,j=1,...,N+nR−1,bij={1,0,i=j−nR+1其他(32)

通过对 S c \boldsymbol{S}c Sc 的每一列执行快速傅里叶变换（FFT），我们得到 S c _ F D \boldsymbol{S}{c\FD} Sc_FD。我们将 S c _ F D \boldsymbol{S}{c\FD} Sc_FD 按行均匀地分为 M 个子带。 N = M N s N = M N_s N=MNs，其中 N s N_s Ns 是一个子带的长度。为了表达简练， S c _ F D \boldsymbol{S}{c\_FD} Sc_FD 的第 m 个子带分量记为 X m \boldsymbol{X}_m Xm。

此外，监视向量 s surv s_{\text{surv}} ssurv 的第 m 个子带分量记为 s surv_FD m s_{\text{surv\_FD}}^m ssurv_FDm。GSC 随后可以公式化为以下 LS 问题：

min ⁡ α ∥ s surv_FD m − X m α ∥ 2 (33) \min_{\boldsymbol{\alpha}} \| \boldsymbol{s}_{\text{surv\_FD}}^m - \boldsymbol{X}_m \boldsymbol{\alpha} \|^2 \tag{33} αmin∥ssurv_FDm−Xmα∥2(33)

参考附录 B 中的推导，我们得到式 (33) 的解如下：

α = ( X m H X m ) † X m H s surv_FD m (34) \boldsymbol{\alpha} = (\boldsymbol{X}_m^H \boldsymbol{X}_m)^{\dagger} \boldsymbol{X}m^H \boldsymbol{s}{\text{surv\_FD}}^m \tag{34} α=(XmHXm)†XmHssurv_FDm(34)

注意此处应使用 Moore-Penrose 逆矩阵。杂波消除后的信号符合以下形式：

s GSC_FD m = s surv_FD m − X m α = s surv_FD m − X m ( X m H X m ) † X m H s surv_FD m (35) \begin{aligned} \boldsymbol{s}_{\text{GSC\FD}}^m &= \boldsymbol{s}{\text{surv\_FD}}^m - \boldsymbol{X}m \boldsymbol{\alpha} \\ &= \boldsymbol{s}{\text{surv\_FD}}^m - \boldsymbol{X}_m (\boldsymbol{X}_m^H \boldsymbol{X}_m)^{\dagger} \boldsymbol{X}m^H \boldsymbol{s}{\text{surv\_FD}}^m \end{aligned} \tag{35} sGSC_FDm=ssurv_FDm−Xmα=ssurv_FDm−Xm(XmHXm)†XmHssurv_FDm(35)

子带合成可以表示如下：

s GSC_FD = [ ( s GSC_FD 1 ) T , ( s GSC_FD 2 ) T , ... , ( s GSC_FD M ) T ] T (36) \boldsymbol{s}_{\text{GSC\FD}} = [(\boldsymbol{s}{\text{GSC\FD}}^1)^T, (\boldsymbol{s}{\text{GSC\FD}}^2)^T, \dots, (\boldsymbol{s}{\text{GSC\_FD}}^M)^T]^T \tag{36} sGSC_FD=[(sGSC_FD1)T,(sGSC_FD2)T,...,(sGSC_FDM)T]T(36)

对应的时域信号如下：

s GSC = IFFT { s GSC_FD } (37) \boldsymbol{s}{\text{GSC}} = \text{IFFT} \{ \boldsymbol{s}{\text{GSC\_FD}} \} \tag{37} sGSC=IFFT{sGSC_FD}(37)

其中 IFFT 表示逆 FFT。