4神经网络框架

神经网络框架

一、线性模型的局限性

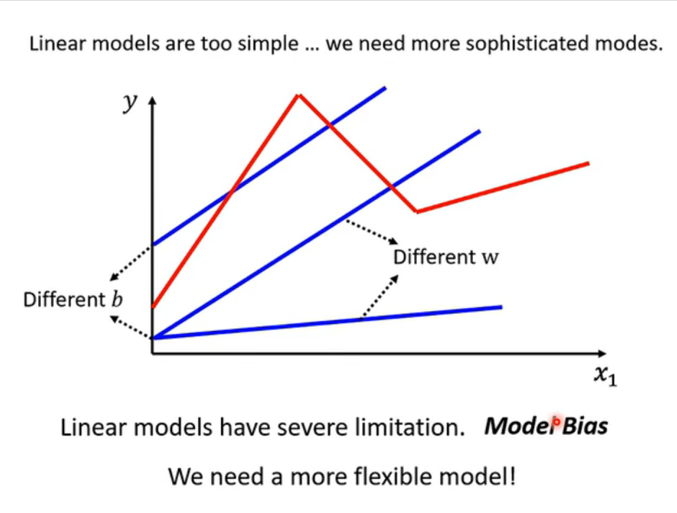
• 模型偏差：无论我们怎么调整参数 www（斜率）和 bbb（截距），直线永远是直线。

  • 这就好比我想让你用一把直尺画出一个圆，无论你怎么摆弄这把尺子，你都画不出圆来。
  • 这不仅是参数选得对不对的问题，而是模型的这种形式本身就太简陋了 。

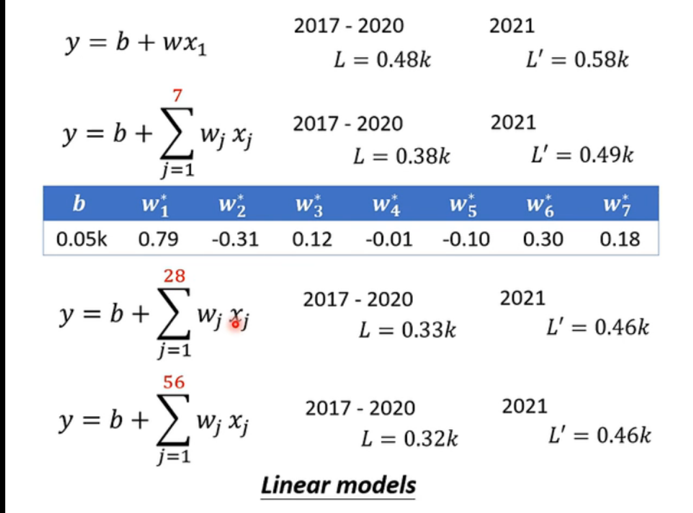
• 在彻底抛弃线性模型之前，这张图展示了另一种努力方向：增加特征。

  • 既然只看"前1天"的数据预测不准，那我看"前7天"、"前28天"甚至"前56天"呢？
  • 表格显示，随着观察天数 jjj 的增加，Loss 确实从 0.48k 降到了 0.32k。这说明更多的数据 确实有帮助，但如果数据本身的规律是非线性的（比如周末效应、突发事件），光靠堆数据还是无法达到极致。

二、分段线性曲线

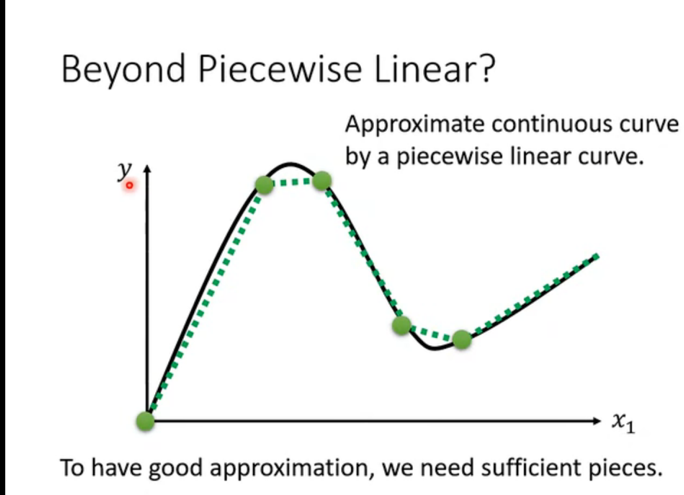
• 虽然一条直线不能弯曲，但如果我们用很多条短的直线连在一起（绿色的虚线），就可以逼近任何复杂的黑色曲线了。这就是 Piecewise Linear Curve。片段越多，拟合得就越像。

• 积木原理 ：数学家发现了一个极其巧妙的方法：复杂的折线 = 常数 + 一堆蓝色的"Z字形"线段之和。只要我们将这些蓝色的基础组件叠加起来，就能拼凑出锯齿状、山峰状等各种形状。

三、Sigmoid 函数

​ 蓝色的"Z字形"线段（Hard Sigmoid）有一个缺点：在拐角处也是直角的，这在数学上不可导 （没法算梯度）。于是，我们需要把它打磨得圆润一点。

• Sigmoid：我们将硬邦邦的折线，换成光滑的 S型曲线，这就是大名鼎鼎的 Sigmoid Function。

  公式如下：
  y=c11+e−(b+wx1) y = c \frac{1}{1 + e^{-(b + w x_1)}} y=c1+e−(b+wx1)1

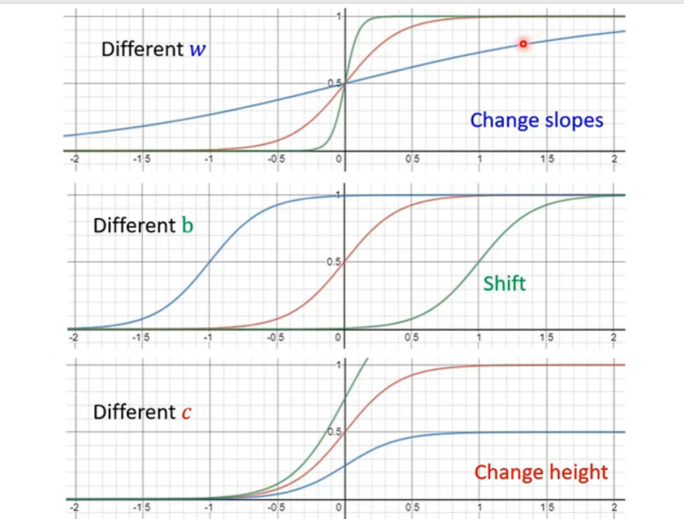
• 三个关键变量：要理解 Sigmoid，必须搞懂这三个参数的作用，它们决定了"S"长什么样：

  1. www (Weight) ：控制斜率 。
     • www 越大，S型越陡峭（越像直角的台阶）。
     • www 越小，S型越平缓。
  2. bbb (Bias) ：控制左右平移 。
     • 改变 bbb，S曲线就会在横轴上左右移动，决定了"台阶"在什么位置发生。
  3. ccc ：控制高度 。
     • 决定了 S 曲线最高能达到多少。

四、神经网络的雏形

• 叠加构造：

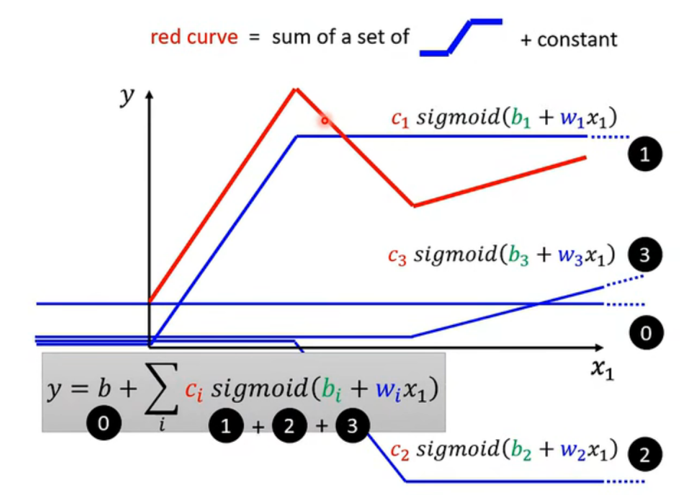
  • 黑色线 (0)：这是一个常数基准线 (Bias)。

  • 蓝色线 (1, 2, 3) ：这是三个不同形状（不同 w,b,cw, b, cw,b,c）的 Sigmoid 函数。

  • **红色线：**它是所有线的总和。
    Red=(0)+(1)+(2)+(3) Red = (0) + (1) + (2) + (3) Red=(0)+(1)+(2)+(3)

• 叠加之后我们得到了一个新的、强大的模型公式：
  y=b+∑ici⋅sigmoid(bi+wix1) y = b + \sum_{i} c_i \cdot \text{sigmoid}(b_i + w_i x_1) y=b+i∑ci⋅sigmoid(bi+wix1)

  • x1x_1x1 是输入。
  • wi,biw_i, b_iwi,bi 是里面的参数。
  • sigmoidsigmoidsigmoid 是**激活函数 **。
  • cic_ici 是外面的权重。
  • ∑\sum∑ 是求和。

五、神经网络：

1.引入更多特征

​ 在现实中，预测往往需要更多线索，比如前天的 x2x_2x2、大前天的 x3x_3x3。

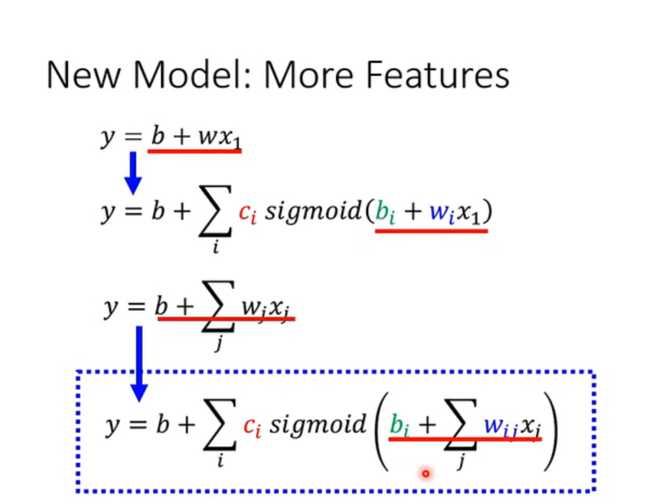
• 公式升级：

  • 原来的输入只是 wix1w_i x_1wix1。
  • 现在变成了 ∑jwijxj\sum_j w_{ij} x_j∑jwijxj。这里的 jjj 代表第几个特征，iii 代表第几个 Sigmoid 函数（神经元）。
  • 这意味着：每一个神经元都要看所有的输入特征 。

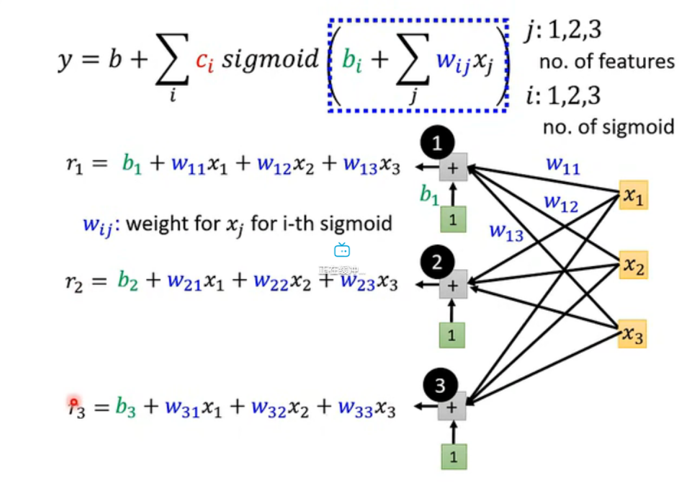
• 连接方式：

  • 看图中的连线，左边的 x1,x2,x3x_1, x_2, x_3x1,x2,x3 是输入层。
  • 中间的 1, 2, 3 是三个神经元。
  • 你会发现这是一张全连接 的图：所有的 xxx 都连向了所有的神经元。
  • 比如第一个神经元计算 r1r_1r1，它就需要用到 w11,w12,w13w_{11}, w_{12}, w_{13}w11,w12,w13 三个权重。

2. 矩阵化

​ 因为在实际应用中，特征和神经元数量常常非常巨大，为了简化表达式，我们引入矩阵 。

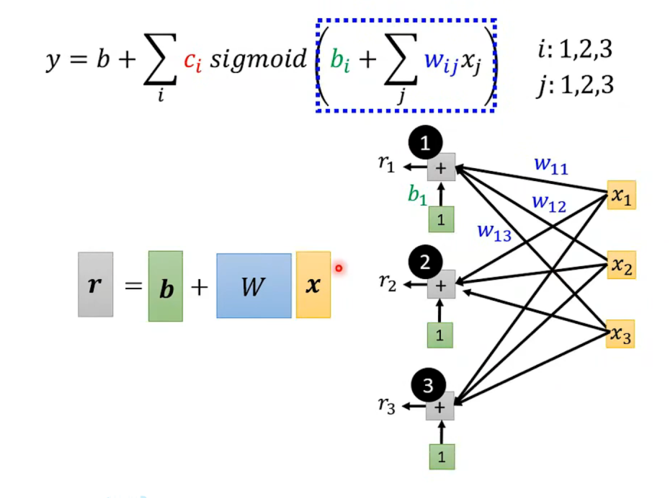
• 堆叠变量：

  • 把输入 x1,x2,x3x_1, x_2, x_3x1,x2,x3 竖着排成一个向量 x\mathbf{x}x。
  • 把三个神经元的偏置 b1,b2,b3b_1, b_2, b_3b1,b2,b3 排成向量 b\mathbf{b}b。
  • 把所有的权重 wijw_{ij}wij 排成了一个矩阵 W\mathbf{W}W 。
    • 第一行放的是第一个神经元关心的权重。
    • 第二行放的是第二个神经元关心的权重。

• 原本复杂的求和公式，现在变成了一个优雅的矩阵乘法公式：
  r=b+Wx \mathbf{r} = \mathbf{b} + \mathbf{W}\mathbf{x} r=b+Wx

3. 激活与输出

​ 算出了 r\mathbf{r}r 还没完，别忘了我们要把直线变弯，得通过 Sigmoid 函数。

1. 激活 ：
   • 我们将向量 r\mathbf{r}r 中的每一个元素都扔进 Sigmoid 函数。
   • 得到新的向量 a\mathbf{a}a ，这就是隐藏层的输出。
   • a=σ(r)\mathbf{a} = \sigma(\mathbf{r})a=σ(r)
2. 线性组合 ：
   • 这步回到了我们最初的想法：把所有 Sigmoid 的结果加权求和。
   • 我们有一组新的权重 c1,c2,c3c_1, c_2, c_3c1,c2,c3（向量 c\mathbf{c}c）和一个最终的偏置 bbb。
   • 公式：y=b+cTay = b + \mathbf{c}^T \mathbf{a}y=b+cTa （这里 cT\mathbf{c}^TcT 表示转置，为了做向量点积）。
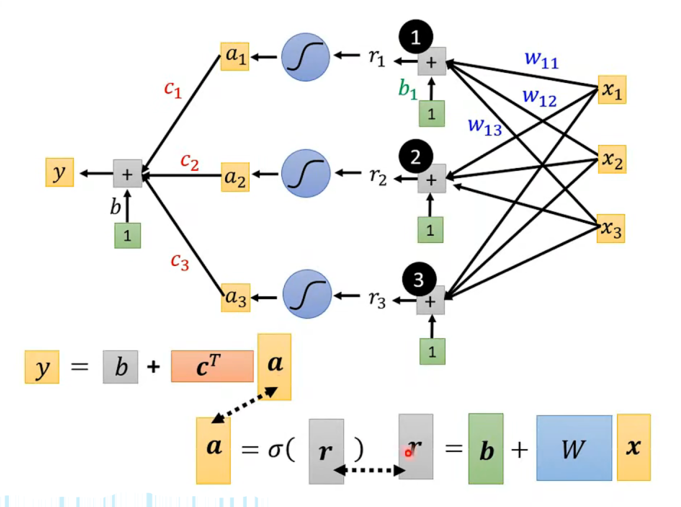
3. 全貌图 ：
   • 把上面所有步骤连起来，就是这张图。
   • 输入 x\mathbf{x}x →\rightarrow→ 线性变换 (W,b\mathbf{W}, \mathbf{b}W,b) →\rightarrow→ 激活 (σ\sigmaσ) →\rightarrow→ 线性组合 (c,b\mathbf{c}, bc,b) →\rightarrow→ 输出 yyy。
   • 这就是一个标准的单隐层神经网络。

4.我们要"学"什么？

​ 回到最开始的问题：机器学习就是找一个函数。现在函数形式定了（就是上面那一长串矩阵公式），那未知数是什么？

• 参数集合 θ\thetaθ ：
  • 我们把所有的未知数统统打包在一起，统称为 θ\thetaθ。
  • 它包括：
    1. 矩阵 W\mathbf{W}W 里的每一个数字（控制神经元怎么看输入）。
    2. 向量 b\mathbf{b}b 里的每一个数字（控制 Sigmoid 的平移）。
    3. 向量 cT\mathbf{c}^TcT 里的每一个数字（控制每个 Sigmoid 的高度）。
    4. 标量 bbb（控制最终结果的基准线）。

​ 其实这和我的上篇文章中提到的一开始学的 y=b+wxy = b + wxy=b+wx 没有本质区别。只不过现在：

• xxx 变成了向量 x\mathbf{x}x。
• www 变成了矩阵 W\mathbf{W}W 和向量 c\mathbf{c}c。
• 运算过程多了一个 Sigmoid 拐弯。

六、深度学习

1. 从 Sigmoid 到 ReLU

​ 在很长一段时间里，Sigmoid 是大家最常用的激活函数。但后来大家发现了一个更简单、更好用的函数，叫做 **ReLU **。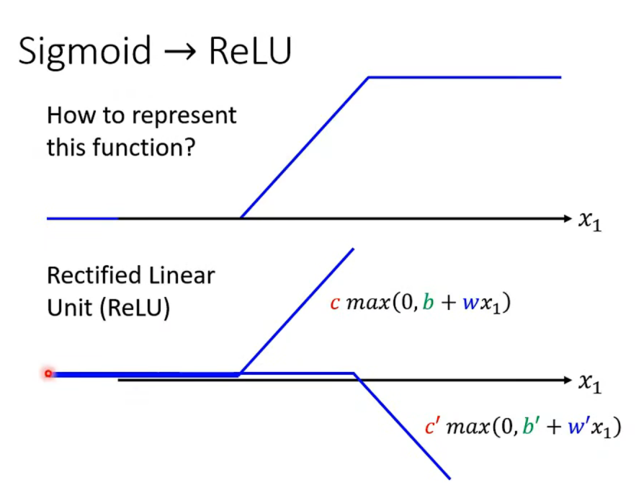

1. ReLU 是什么？
   • 公式为c⋅max⁡(0,b+wx1)c \cdot \max(0, b + wx_1)c⋅max(0,b+wx1)。
   • 它的逻辑简单到令人发指：
     • 如果算出来的数是负的，就让它等于 0。
     • 如果算出来的数是正的，就保持原样。
   • 图像上看，它就是一个折角。
2. 为什么要用 ReLU？
   • 还记得我们之前用 Sigmoid 拼凑各种曲线吗？
   • 图中展示了数学上的一个巧妙关系：2 个 ReLU 可以合成 1 个"Hard Sigmoid"的形状。
   • 既然 ReLU 是更小的积木，那我们直接用 ReLU 堆叠，也能拼出任何复杂的曲线，而且它的计算量比指数运算（Sigmoid 里的 e−xe^{-x}e−x）小得多.

2. 多层神经元堆叠

既然我们可以有一层神经元，为什么不能有两层、三层、甚至一百层呢？这就是深度学习 中"深度"二字的由来。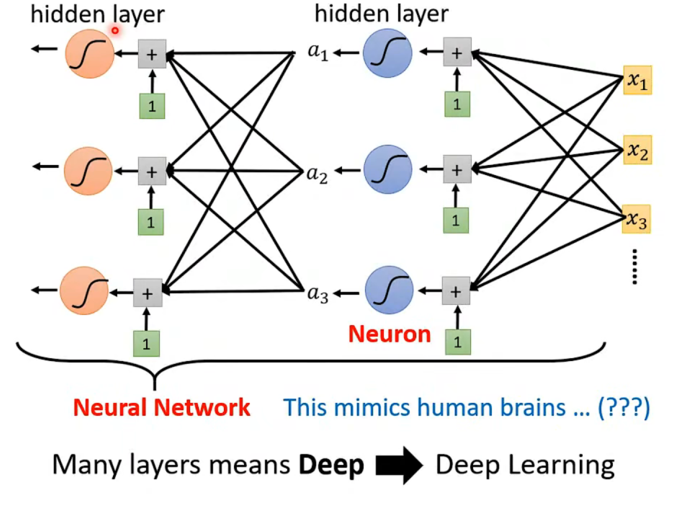

• 层层递进 ：
  • Input (xxx)：输入数据。
  • Layer 1 (aaa) ：第一层神经元接收输入，计算出一组激活值 a\mathbf{a}a。公式：a=σ(b+Wx)\mathbf{a} = \sigma(\mathbf{b} + \mathbf{W}\mathbf{x})a=σ(b+Wx)。
  • Layer 2 (a′a'a′) ：关键点在这里！ 第二层神经元把第一层的输出 a\mathbf{a}a 当作自己的输入。公式：a′=σ(b′+W′a)\mathbf{a}' = \sigma(\mathbf{b}' + \mathbf{W}'\mathbf{a})a′=σ(b′+W′a)。
  • 以此类推，我们可以不断递进。

3. 机器学习3部曲

​ 虽然模型变复杂了，但我们的核心方法论（三部曲）依然没变：

1. Function (模型)：

   • 函数更复杂了，变成了一串连环套的矩阵运算：
     y=b+cTσ(b+Wx) y = b + c^T \sigma(b + Wx) y=b+cTσ(b+Wx)

2. Loss (损失)：

   • 依然是计算预测值 yyy 和真实值之间的差距（比如 MSE）。

3. Optimization (优化)：

   • 依然是用梯度下降来找参数。只不过现在要找的参数 W,b,W′...\mathbf{W}, \mathbf{b}, \mathbf{W}'...W,b,W′... 更多了，计算梯度需要用到反向传播算法。