L1范数，L2范数，L3范数，切比雪夫距离

文章目录

• 前言
• 一、L1范数
• 二、L2范数
• 三、L3距离
• 四、切比雪夫距离
• 总结

---

前言

L1范数，L2范数，L3范数，切比雪夫距离。

---

一、L1范数

1. 定义：L1范数，也称为绝对误差或曼哈顿距离，是一种用于度量向量或数据集 之间差异 的方法。它的计算是通过求每个元素的绝对差值 并对其求和。
2. 名称来源: 来源于纽约曼哈顿的网格状街道，从一个点到另一个点只能沿水平或垂直方向移动，而不能走对角线。
3. 数学公式：对于一个向量x = [x1,x2,...,xn]，和另一个向量y = [y1,y2,...,yn]，其L1范数定义为：|| Error || = |x1 - y1|+|x2 - y2|+...+|xn - yn|。
4. 示例图：
   
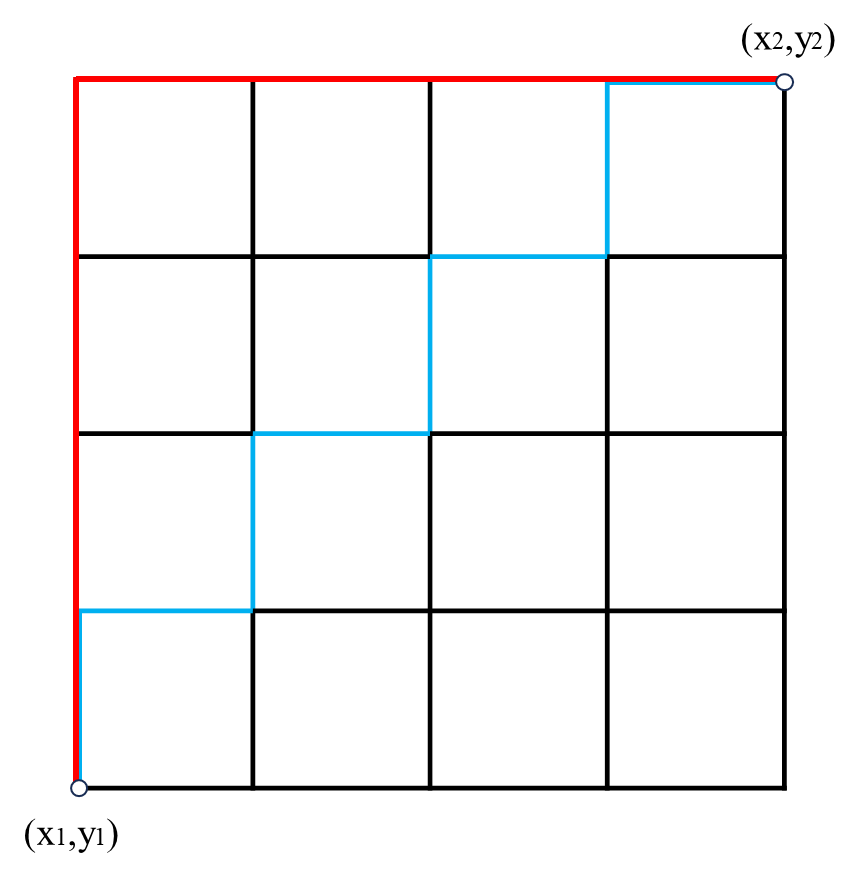
   这表示二维空间中的曼哈顿距离（红色和蓝色线表示），L1范数 = |x1 - x2| + | y1 - y2 |。
5. 优点：
   对异常值不敏感，适合数据中可能存在噪声或异常值的情况。
   相较于L2，优化过程更加稳健，且计算量较小。
6. 缺点：
   可能会导致解的不够平滑，在某些问题中，L1范数可能无法找到足够精确的解，尤其是在数据没有异常值时，L2范数的效果可能更好。

优缺点解释：

1. 对异常值不敏感：L1范数对离群点的影响较小，因为它只计算误差的绝对值，而不对大误差进行平方加重。
2. 相较L2，优化过程更稳健：L1范数适用于数据中可能存在异常值的情况。它不会像L2范数那样放大大的误差，使得异常值不会对模型产生过大影响。
3. 计算量较小：不需要平方。
4. 解不够光滑： y = |x|，在 x=0 处左右导数不相等，从数学上破坏了"光滑"（可微）的要求。

二、L2范数

1. 定义:：欧式距离，也叫做欧几里得距离，用于计算两点之间的直线距离。
2. 来源：它来源于古希腊数学家欧几里得（Euclid），在其《几何原本》一书中首次提出。
3. 数学公式：
   
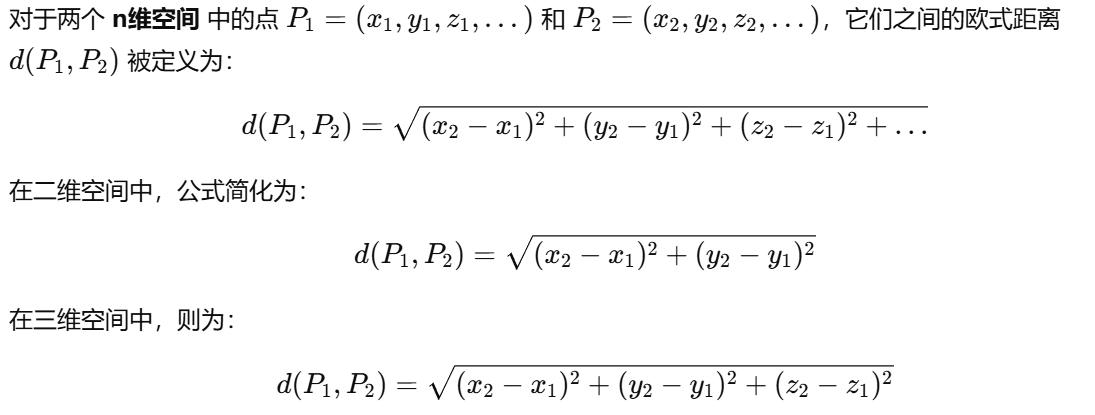
4. 优点：
   欧式距离非常直观，容易理解和计算。
   它是最常见的距离度量方式，适用于多种实际应用（如KNN、聚类、图像识别等）。
   它准确地衡量了两点间的直线最短距离，符合我们日常生活中的直觉。
5. 缺点：
   在高维空间中，欧式距离的效果可能会变差（维度灾难 ）。在高维空间里，不同数据点之间的距离趋于相似，欧式距离可能无法有效区分不同的数据点。
   如果数据中的特征有不同的量纲（比如一个特征是体重，另一个特征是年龄），欧式距离的计算可能会受到不同尺度的影响，导致距离计算不准确。在这种情况下，常常需要进行 标准化 或 归一化 。
   欧式距离假设两点之间是通过直线连接的，但在某些问题中，数据可能具有复杂的非线性关系，欧式距离在这种情况下可能不合适。
6. 示例图：
   
   这表示欧式距离（红色斜线），距离为两点之间的直线距离。

三、L3距离

1. 定义：L3范数，顾名思义，是一种类似于L1范数和L2范数的距离度量方法，但它在计算时使用了立方差的方式。它用于衡量向量或点之间的距离，但与 L1 和 L2 范数相比，L3范数的惩罚方式有所不同。
2. 数学定义：
   

四、切比雪夫距离

1. 定义：切比雪夫距离（Chebyshev Distance）是衡量两个点之间"最大轴向差异"的距离度量。它也被称为 最大范数 或 L∞ 范数。在计算两点之间的距离时，切比雪夫距离选择了 所有坐标轴方向上最大的差值。
2. 数学定义：
   

总结

后续更多距离会进行补充。