文章目录
-
- 摘要
- Abstract
-
- [1.1 传统优化算法](#1.1 传统优化算法)
- 1.2高纬度多目标优化算法
- 总结
摘要
本周学习了传统优化算法在高纬度失效的场景,并且实现了基于分解的MOEA/D-DRA算法来适应高纬度优化。
Abstract
This week, we studied the scenarios where traditional optimization algorithms fail in high-dimensional spaces and implemented the decomposition-based MOEA/D-DRA algorithm to adapt to high-dimensional optimization.
1.1 传统优化算法
NSGA-II在高纬度时, 以上是NGSA-II在目标维度是10,种群大小为300,迭代250次之后得到的最终结果,发现NGSA-II的帕累托更杂乱,解没有收敛到清晰的帕累托前沿,而是均匀地、随机地散布在整个目标空间的中间区域。几乎所有线条都穿过了每个目标从0到1的几乎所有值。这意味着很多解在各个目标上都表现平庸,且互相之间不构成明显的支配关系。
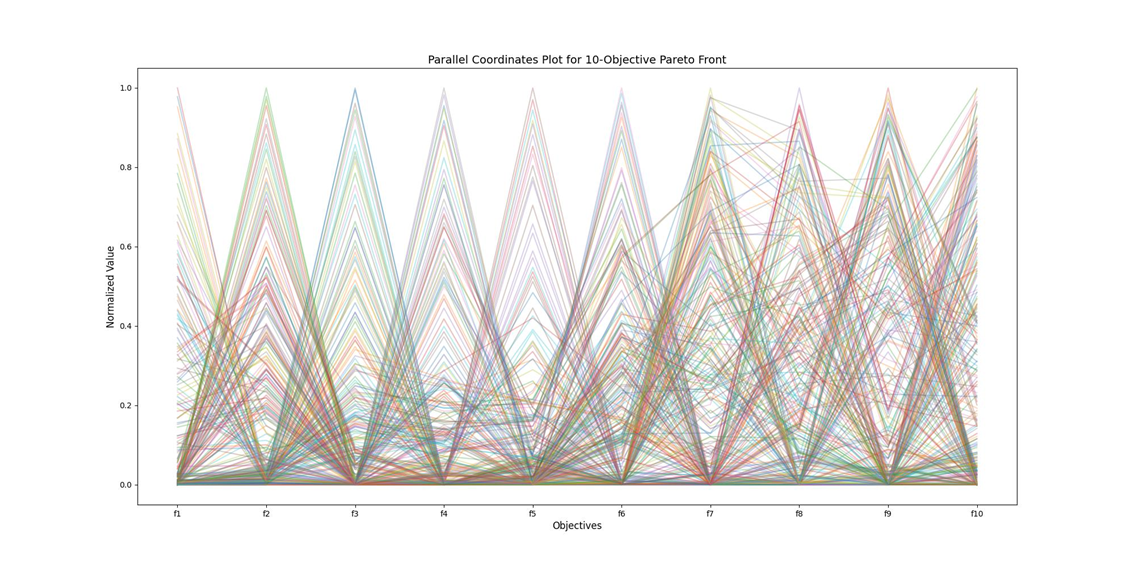
1.2高纬度多目标优化算法
MOEA/D-DRA 的核心思想是将 10 目标优化问题分解为多个单目标子问题,通过动态分配搜索资源提升整体优化效果,具体机制如下:
问题分解机制
MOEA/D-DRA 是在 MOEA/D 框架基础上发展而来的改进版本。MOEA/D 通过将多目标问题分解为多个标量子问题,并利用一组均匀分布的权重向量来引导搜索方向。每个子问题对应一个权重向量,并通过聚合函数(如 Tchebycheff 函数)将多目标问题转化为单目标问题:
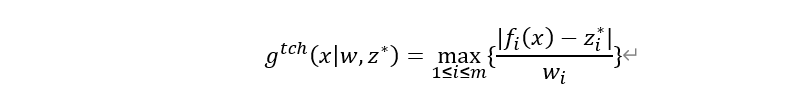
其中w是权重向量,z^*为理想点。
与标准 MOEA/D 不同,MOEA/D-DRA 引入了动态资源分配机制,即根据子问题的"效用"动态选择一部分子问题进行演化,而不是对所有子问题一视同仁。这种机制的核心在于:
效用函数定义:每个子问题的效用π^i反映了其在最近若干代中的改进程度。具体定义为:
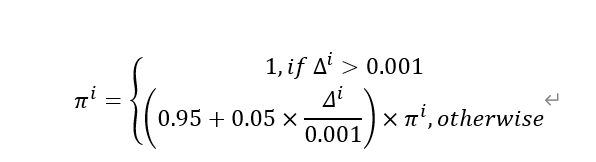
其中Δ^i 是子问题i的适应度改进率,计算如下:
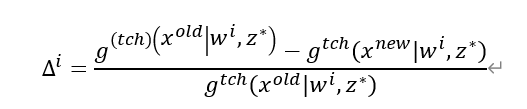
该值越大,说明该子问题在最近的优化中获得了更大的改进,因此更值得投入计算资源。
资源分配策略:在每一代中,算法根据效用值对所有子问题进行排序,优先选择效用高的子问题进行繁殖和更新。这种策略可以有效集中计算资源于"有潜力"的搜索区域,从而提升整体收敛速度和解集质量。
动态资源分配(DRA)
效用评估:根据子问题的历史改进情况计算效用值,反映子问题的优化潜力;
资源倾斜:将搜索资源优先分配给效用值高的子问题,提高搜索效率;
休眠激活:定期激活效用值过低的 "休眠" 子问题,避免算法早熟收敛。
邻域协作机制
为每个子问题构建邻域结构(基于权重向量的欧氏距离);
子问题的演化仅在其邻域内选择父代,保持解的局部一致性;
通过邻域更新实现子问题间的信息共享,促进帕累托前沿的整体推进。
python
import random
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
np.random.seed(42)
random.seed(42)
def dtlz1(x, m):
x = np.asarray(x)
n = len(x)
k = n - m + 1
assert k >= 1, "n must be >= m"
g = 100 * (k + np.sum((x[-k:] - 0.5) ** 2 - np.cos(20 * np.pi * (x[-k:] - 0.5))))
f = []
for i in range(m):
fi = 0.5 * (1 + g)
for j in range(m - i - 1):
fi *= x[j]
if i > 0:
fi *= (1 - x[m - i - 1])
f.append(fi)
return np.array(f)
def fast_non_dominated_sort(objectives):
objectives = np.array(objectives)
n = objectives.shape[0]
domination_count = np.zeros(n, dtype=int)
# 被支配的集合
dominated_set = [[] for _ in range(n)]
# 前沿列表
fronts = []
for i in range(n):
for j in range(n):
if i == j:
continue
# 检查i是否支配j
if np.all(objectives[i] <= objectives[j]) and np.any(objectives[i] < objectives[j]):
dominated_set[i].append(j)
# 检查j是否支配i
elif np.all(objectives[j] <= objectives[i]) and np.any(objectives[j] < objectives[i]):
domination_count[i] += 1
# 找到第一前沿(非支配解)
current_front = [i for i in range(n) if domination_count[i] == 0]
fronts.append(current_front)
# 寻找后续前沿
while current_front:
next_front = []
for i in current_front:
for j in dominated_set[i]:
domination_count[j] -= 1
if domination_count[j] == 0:
next_front.append(j)
if next_front:
fronts.append(next_front)
current_front = next_front
return fronts
def crowed_distance_assignment(objectives):
pop_size, num_objectives = objectives.shape
distances = np.zeros(pop_size)
for m in range(num_objectives):
indices = np.argsort(objectives[:, m])
distances[indices[0]] = np.inf # 边界个体
distances[indices[-1]] = np.inf # 边界个体
norm = objectives[indices[-1], m] - objectives[indices[0], m]
if norm == 0: continue # 如果所有目标值相同,则跳过
for i in range(1, pop_size - 1):
distances[indices[i]] += (objectives[indices[i + 1], m] - objectives[indices[i - 1], m]) / norm
return distances
def sbx_crossover(parent1, parent2, eta, bounds, crossover_rate=1.0):
if random.random() > crossover_rate:
return np.array(parent1), np.array(parent2)
parent1 = np.array(parent1)
parent2 = np.array(parent2)
vars = len(parent1)
child1 = np.copy(parent1)
child2 = np.copy(parent2)
for i in range(vars):
x1 = parent1[i]
x2 = parent2[i]
low, high = bounds[i]
if abs(x1 - x2) < 1e-14:
child1[i] = x1
child2[i] = x2
continue
if x1 > x2:
x1, x2 = x2, x1
swapped = True
else:
swapped = False
u = random.random()
if u <= 0.5:
beta = (2.0 * u) ** (1.0 / (eta + 1.0))
else:
beta = (1.0 / (2.0 * (1.0 - u))) ** (1.0 / (eta + 1.0))
c1 = 0.5 * ((1 + beta) * x1 + (1 - beta) * x2)
c2 = 0.5 * ((1 - beta) * x1 + (1 + beta) * x2)
c1 = np.clip(c1, low, high)
c2 = np.clip(c2, low, high)
if swapped:
child1[i] = c2
child2[i] = c1
else:
child1[i] = c1
child2[i] = c2
return child1, child2
def polynomial_mutation(entry, bounds, mutation_rate=1.0, eta=20):
individual = np.array(entry, dtype=float)
mutated = np.copy(individual)
n = len(individual)
for i in range(n):
if random.random() >= mutation_rate:
continue
low, high = bounds[i]
y = mutated[i]
u = random.random()
if u <= 0.5:
delta = (2 * u) ** (1.0 / (eta + 1)) - 1.0
else:
delta = 1.0 - (2 * (1 - u)) ** (1.0 / (eta + 1))
y_new = y + delta * (high - low)
y_new = np.clip(y_new, low, high)
mutated[i] = y_new
return mutated
def binary_tournament_selection(population, rank, crowding_distances):
pop_size = len(population)
idx1, idx2 = np.random.choice(pop_size, 2, replace=False)
# 优先选择rank小的
if rank[idx1] < rank[idx2]:
return population[idx1]
elif rank[idx1] > rank[idx2]:
return population[idx2]
else:
# rank相同,选择拥挤距离大的
if crowding_distances[idx1] > crowding_distances[idx2]:
return population[idx1]
else:
return population[idx2]
def generate_weight(N, m):
return np.random.dirichlet(np.ones(m), size=N)
def tchebycheff(y, weight, z):
return np.max(weight * np.abs(y - z))
def differential_evolution(parent1, parent2, parent3, F=0.5):
parent1 = np.array(parent1)
parent2 = np.array(parent2)
parent3 = np.array(parent3)
# 基本差分变异
mutant = parent1 + F * (parent2 - parent3)
return mutant
def compute_utility(old_objs, new_objs, weights, z, delta=1e-8):
old_val = tchebycheff(old_objs, weights, z)
new_val = tchebycheff(new_objs, weights, z)
if abs(old_val) < delta:
return 0.0
improvement = (old_val - new_val) / old_val
return max(0.0, improvement) # 只考虑改进
# 动态资源分配选择
def dra_selection(pi, k):
n = len(pi)
k = min(k, n)
norm = pi + 1e-10
pi_min, pi_max = norm.min(), norm.max()
if pi_max - pi_min > 1e-10:
pi_norm = (norm - pi_min) / (pi_max - pi_min)
else:
pi_norm = np.ones(n)
p = pi_norm / pi_norm.sum()
if np.any(np.isnan(p)) or np.any(p < 0):
p = np.ones(n) / n
selected = np.random.choice(n, size=k, p=p, replace=False)
return selected
def evaluate_population(population, m):
objectives = []
for ind in population:
objs = dtlz1(ind, m)
objectives.append(objs)
return np.array(objectives)
def MOEA(m=10, D=30, n=200, max_gen=500, mutation_rate=0.0, delta=0.8, nr=2,
crossover_rate=0.9, sbx_eta=20, poly_eta=20, ref_point=None):
lambdas = generate_weight(n, m) # shape (N, m)
T = min(30, n)
neighbors = []
bounds = [(0.0, 1.0)] * D
# 计算邻居
for i in range(n):
dists = np.linalg.norm(lambdas - lambdas[i], axis=1)
idx = np.argsort(dists)[:T]
neighbors.append(idx)
# 初始化种群
population = np.random.rand(n, D)
objectives = evaluate_population(population, m)
z = np.min(objectives, axis=0) # shape (m,)
pi = np.ones(n)
gen = 0
f_history = objectives.copy() # shape (N, m)
hv_history = []
while gen < max_gen:
# 使用dra_selection进行动态资源分配选择
selected = set()
# 选择每个目标上的最优解
for obj in range(m):
idx = np.argmin(objectives[:, obj])
selected.add(idx)
# 使用dra_selection选择剩余个体
remaining = max(1, n // 5 - len(selected)) # 确保至少选择1个
if remaining > 0:
selected_indices = dra_selection(pi, remaining)
selected.update(selected_indices)
I = list(selected)
# 对选中的个体进行进化操作
for i in I:
# 选择邻域或整个种群
if np.random.rand() < delta:
P = neighbors[i].copy()
else:
P = np.arange(n).copy()
if len(P) < 2:
continue
# 选择父代
a, b = np.random.choice(P, size=2, replace=False)
x1, x2 = population[a], population[b]
# SBX交叉
child1, child2 = sbx_crossover(x1, x2, sbx_eta, bounds, crossover_rate)
# 多项式变异
child1 = polynomial_mutation(child1, bounds, mutation_rate, poly_eta)
child2 = polynomial_mutation(child2, bounds, mutation_rate, poly_eta)
# 评估子代
y1 = dtlz1(child1, m)
y2 = dtlz1(child2, m)
# 更新理想点
z = np.minimum(z, y1)
z = np.minimum(z, y2)
# 更新邻域解
for child, y in [(child1, y1), (child2, y2)]:
utilities = []
for j in P:
old_objs = objectives[j]
utility = compute_utility(old_objs, y, lambdas[j], z)
utilities.append((j, utility))
# 选择效用最大的nr个进行更新
utilities.sort(key=lambda x: x[1], reverse=True)
for j, utility in utilities[:nr]:
if utility > 0: # 只有改进才更新
population[j] = child
objectives[j] = y
gen += 1
if gen % 50 == 0:
for i in range(n):
old_objs = f_history[i]
new_objs = objectives[i]
utility = compute_utility(old_objs, new_objs, lambdas[i], z)
if utility < 0.001:
pi[i] *= 0.95 # 效用低,减少资源分配
else:
pi[i] = min(pi[i] * 1.05, 2.0) # 效用高,增加资源分配
f_history = objectives.copy()
if gen % 10 == 0:
f = fast_non_dominated_sort(objectives)
hv = hypervolume(objectives[f[0]], ref_point, n_samples=200000)
hv_history.append((gen, hv))
avg_g = np.mean([tchebycheff(objectives[i], lambdas[i], z) for i in range(n)])
print(f"Generation {gen}, Avg Tchebycheff: {avg_g:.4f}, HV: {hv:.4f}")
return population, objectives, z, hv_history
def NSGA(m=10, D=30, n=200, max_gen=500, crossover_rate=0.9, mutation_rate=0.0, sbx_eta=20, poly_eta=20,
ref_point=None):
bounds = [(0.0, 1.0)] * D
population = np.random.rand(n, D)
objectives = evaluate_population(population, m) # shape (pop_size, m)
hv_history = []
f = fast_non_dominated_sort(objectives)
rank = np.zeros(n, dtype=int)
for i, front in enumerate(f):
for idx in front:
rank[idx] = i
crowding_distances = crowed_distance_assignment(objectives)
gen = 0
while gen < max_gen:
offspring = []
while len(offspring) < n:
# 选择两个父代
parent1 = binary_tournament_selection(population, rank, crowding_distances)
parent2 = binary_tournament_selection(population, rank, crowding_distances)
# SBX 交叉
child1, child2 = sbx_crossover(parent1, parent2, sbx_eta, bounds, crossover_rate)
# 多项式变异
child1 = polynomial_mutation(child1, bounds, mutation_rate, poly_eta)
child2 = polynomial_mutation(child2, bounds, mutation_rate, poly_eta)
offspring.append(child1)
offspring.append(child2)
offspring = np.array(offspring[:n])
combined_pop = np.vstack([population, offspring]) # (2N, n)
combined_obj = evaluate_population(combined_pop, m) # (2N, m)
fronts = fast_non_dominated_sort(combined_obj)
new_population = []
new_objectives = []
for front in fronts:
if len(new_population) + len(front) <= n:
# 全部加入
new_population.extend(combined_pop[front])
new_objectives.extend(combined_obj[front])
else:
# 按拥挤距离截断
remaining = n - len(new_population)
front_objs = combined_obj[front]
distances = crowed_distance_assignment(front_objs)
# 按拥挤距离降序排序
sorted_indices = np.argsort(-distances) # 负号 → 降序
selected = [front[i] for i in sorted_indices[:remaining]]
new_population.extend(combined_pop[selected])
new_objectives.extend(combined_obj[selected])
break
population = np.array(new_population)
objectives = np.array(new_objectives)
# 更新 rank 和 crowding_distances
fronts_current = fast_non_dominated_sort(objectives)
rank = np.zeros(n, dtype=int)
for i, front in enumerate(fronts_current):
for idx in front:
rank[idx] = i
crowding_distances = crowed_distance_assignment(objectives)
gen += 1
if gen % 10 == 0:
f = fast_non_dominated_sort(objectives)
hv = hypervolume(objectives[f[0]], ref_point, n_samples=200000)
hv_history.append((gen, hv))
print(f"Gen {gen},HV: {hv:.4f}")
ideal = np.min(objectives, axis=0)
return population, objectives, ideal, hv_history
def draw(objs, m, filename):
# 高维目标空间,平行坐标图
plt.figure(figsize=(20, 10))
norm = (objs - objs.min(axis=0)) / (objs.max(axis=0) - objs.min(axis=0) + 1e-10)
for i in range(len(norm)):
plt.plot(range(m), norm[i], alpha=0.3, linewidth=1.5)
plt.xticks(range(m), [f'f{i + 1}' for i in range(m)])
plt.xlabel('Objectives', fontsize=12)
plt.ylabel('Normalized Value', fontsize=12)
plt.title(f'Parallel Coordinates Plot for {m}-Objective Pareto Front', fontsize=14)
plt.grid(True)
plt.savefig('result/' + filename)
plt.show()
def hypervolume(front, ref_point, n_samples=200000):
front = np.array(front)
m = front.shape[1]
min_bound = np.full(m, 0.0)
max_bound = ref_point
samples = np.random.uniform(min_bound, max_bound, size=(n_samples, m))
box = np.prod(max_bound - min_bound)
count = 0
for s in samples:
# 检查是否被 front 中任意一点支配
dominated = np.any(np.all(front <= s, axis=1) & np.any(front < s, axis=1))
if dominated:
count += 1
return (count / n_samples) * box
if __name__ == "__main__":
m = 10
D = 12
n = 300
max_gen = 250
ref_point = np.ones(m) * 1.3
pop, objectives, ideal, hv_m = MOEA(m, D, n, max_gen=max_gen, mutation_rate=1.0 / D, ref_point=ref_point)
print("Final ideal point:", ideal)
print("Population size:", len(pop))
draw(objectives, m=10, filename="MOEA D-DRA.jpg")
df = pd.DataFrame(objectives, columns=[f"f{i + 1}" for i in range(m)])
df.to_csv("MOEA_D_DRA_result.csv", index=False)
pop, objectives, ideal, hv_n = NSGA(m, D, n, max_gen=max_gen, mutation_rate=1.0 / D, ref_point=ref_point)
print("Final ideal point:", ideal)
print("Population size:", len(pop))
draw(objectives, m=10, filename="NGSA-II.jpg")
df = pd.DataFrame(objectives, columns=[f"f{i + 1}" for i in range(m)])
df.to_csv("NSGA-II_result.csv", index=False)
x1, y1 = zip(*hv_m)
x2, y2 = zip(*hv_n)
plt.figure(figsize=(10, 6))
plt.plot(x1, y1, 'o-', label='MOEA/D-DRA', color='blue')
plt.plot(x2, y2, 's-', label='NSGA-II', color='red')
plt.xlabel('Generation')
plt.ylabel('Estimated Hypervolume')
plt.title(f'Hypervolume Comparison (m={m}, Monte Carlo samples={200000})')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.savefig('result/Hypervolume.jpg')
plt.show()最终的结果
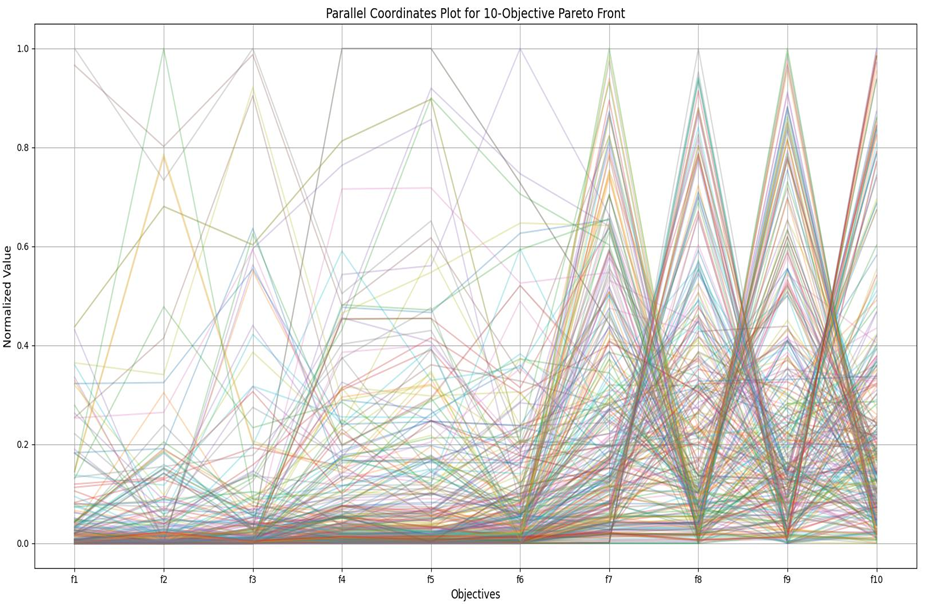
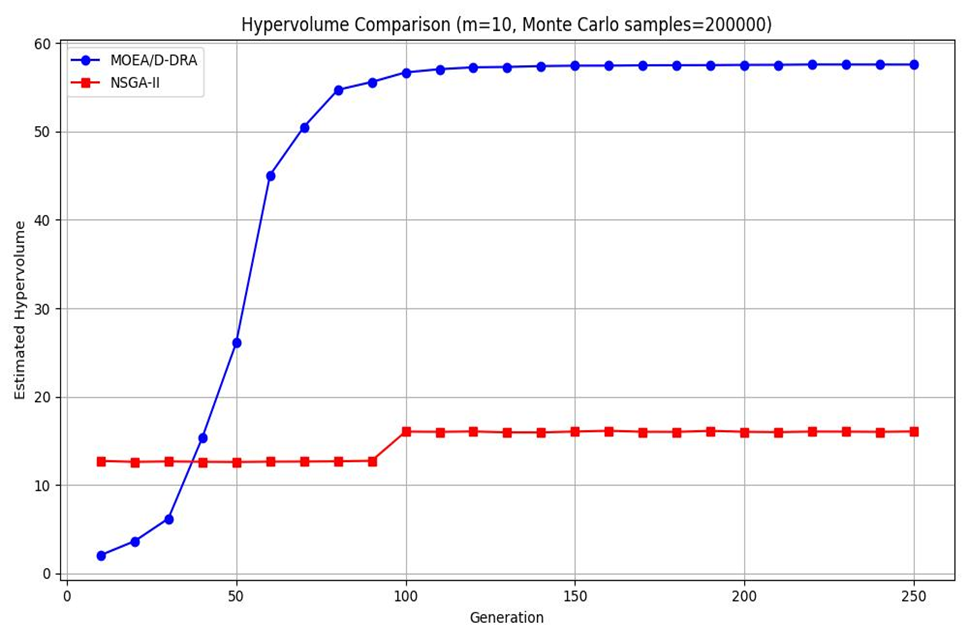
MOEA/D-DRA的超体积逐渐上升,而NSGA-II的超体积却不怎么变化,说明MOEA/D-DRA在高维时对于dtlz1函数具有更好的效果,且MOEA/D-DRA在f1-f5的帕累托前沿的覆盖面更大。
总结
本周主要完成这个高维多目标优化算法。