这篇文章是一篇非常经典的视频稳像的论文。是谷歌 2011 年提出的,据说已经成为了离线防抖算法的标杆,目前 YouTube 里面的很多视频的离线防抖算法就是利用这个方法去做处理的。
Abstract
本文提出一种新颖算法,通过去除非期望运动,自动应用可约束的 L1 最优相机路径来生成稳定视频。我们的目标是计算由恒定段、线性段和抛物线段组成的相机路径,以模拟专业摄影师采用的相机运动方式。为此,该算法基于线性规划框架,旨在最小化所得相机路径的一阶、二阶和三阶导数。我们的方法突破了传统相机路径滤波仅能抑制高频抖动的局限,实现了更优的视频稳定效果。算法中直接融入了对相机路径的额外约束,从而能够生成稳定且经过重定目标处理的视频。该方法无需用户交互,也无需进行昂贵的场景三维重建,可作为任何相机拍摄或在线获取视频的后处理流程。

- 图 1
Introduction
视频稳定化技术旨在生成随手拍摄视频的稳定版本,理想情况下应遵循摄影原则。随手拍摄的视频通常由手机、便携式摄像机等手持设备拍摄,且几乎未使用任何稳定设备。相比之下,专业摄影师会运用各类稳定工具,例如三脚架、相机轨道车和斯坦尼康稳定器。大多数光学稳定系统仅能抑制高频抖动,无法消除手持摇镜拍摄或行走状态下拍摄视频时出现的低频畸变。为克服这一局限,我们提出一种通过去除非期望运动来生成视频稳定版本的算法。该算法作为后处理流程,可应用于任何相机拍摄或在线获取的视频,且无需了解拍摄设备或场景的任何信息。
通常而言,后处理视频稳定化技术 [10] 包含以下三个主要步骤:(1) 估计原始(可能存在抖动的)相机路径;(2) 估计一条新的平滑相机路径;(3) 利用估计出的平滑相机路径合成稳定视频。
本文对上述所有步骤均进行了处理。核心贡献在于提出一种全新算法,用于计算最优稳定相机路径。我们建议让一个固定宽高比的裁剪窗口沿该路径移动 ------ 该路径经优化后可包含显著点和显著区域,同时基于摄影原则最小化 L1 平滑性约束。我们的技术通过将路径划分为恒定运动、线性运动或抛物运动段,实现平滑路径的最优分段。该方法避免了这三种运动类型的叠加,例如,在恒定段内,路径会保持真正静止,而非存在微小的残余运动。此外,它还能消除低频颠簸(例如由手持相机行走时产生的颠簸)。我们将该优化问题构建为一个受各类约束条件限制的线性规划(Linear Program, LP)问题,例如裁剪窗口需始终包含在帧矩形区域内。因此,我们无需执行额外的运动补绘 [10, 3] 操作,而该操作往往可能产生伪影。
L1 Optimal Camera Paths
从电影摄影角度来看,最舒适的观看体验源于静态相机、安装在三脚架上的摇镜相机或置于轨道车上的相机的运用。这些镜头类型之间的切换可通过剪辑或无抖动过渡实现,即避免加速度的突然变化。
我们期望所计算的相机路径 P ( t ) P(t) P(t) 符合这些电影摄影特性,但不会在原始视频已有的剪辑基础上额外添加新的剪辑。为模拟专业影像效果,我们将路径优化为由以下路径段组成:
- 恒定路径:代表静态相机,即 D P ( t ) = 0 DP(t) = 0 DP(t)=0(其中 D D D 为微分算子);
- 恒定速度路径:代表摇镜或轨道推移镜头,即 D 2 P ( t ) = 0 D^2P(t) = 0 D2P(t)=0;
- 恒定加速度路径:代表静态相机与摇镜相机之间的缓入缓出过渡,即 D 3 P ( t ) = 0 D^3P(t) = 0 D3P(t)=0。
为得到由独立的恒定段、线性段和抛物线段(而非这些段的叠加)组成的最优路径,我们将该优化问题构建为带约束的 L1 最小化问题。L1 优化具有解的稀疏性特征,即会尽可能使路径在多数区间上精准满足上述诸多特性,因此计算得出的路径在大部分段上的导数均严格为零。相比之下,L2 最小化仅能在平均意义上(最小二乘意义下)满足上述特性,导致最终路径存在微小但非零的梯度。从定性角度来看,经 L2 优化得到的相机路径始终存在一些微小的非零运动(大概率与相机抖动方向一致),而我们通过 L1 优化得到的路径则仅由类静态相机段、(匀速)线性运动段和恒定加速度段组成。
我们的目标是找到一条相机路径 P ( t ) P(t) P(t),在满足特定约束条件的前提下,最小化上述目标函数。我们探索了多种约束类型,具体如下:
- 包含约束 Inclusion constraint :经路径 P ( t ) P(t) P(t) 变换后的裁剪窗口,应始终包含在经原始相机路径 C ( t ) C(t) C(t) 变换后的帧矩形区域内。当将其建模为硬约束时,该约束可在保证裁剪窗口内所有像素均包含有效信息的前提下,实现视频稳定化与重定目标处理。
- 邻近约束(Proximity constraint :新的相机路径 P ( t ) P(t) P(t) 应保留原始视频的拍摄意图。例如,若原始路径中包含相机推进(变焦)的片段,最优路径也应遵循这一运动趋势,但需以平滑的方式实现。
- 显著性约束(Saliency constraint) :显著点(例如通过人脸检测器或显著性图中的通用模式提取获得)应被包含在经 P ( t ) P(t) P(t) 变换后的裁剪窗口的全部区域或特定部分内。将该约束建模为软约束具有显著优势,可避免对显著点的追踪 ------ 而这种追踪通常会导致非显著区域产生非平滑运动。
Solution via Linear Programming
在后续讨论中,我们假设原始视频的相机路径 C ( t ) C(t) C(t) 已通过(例如特征点跟踪等方法)计算得出,且在每个时间实例上由参数化线性运动模型描述。具体而言,设视频为图像序列 I 1 , I 2 , ... , I n I_1, I_2, \dots, I_n I1,I2,...,In,其中每帧图像对 ( I t − 1 , I t ) (I_{t-1}, I_t) (It−1,It) 均关联一个线性运动模型 F t ( x ) F_t(x) Ft(x),该模型用于描述特征点 x x x 从帧 I t I_t It 到帧 I t − 1 I_{t-1} It−1 的运动过程。此后,我们将考虑在每帧 I t I_t It 处定义的离散化相机路径 C t C_t Ct。 C t C_t Ct 通过矩阵乘法迭代计算得出,公式如下:
C t + 1 = C t F t + 1 ⟹ C t = F 1 F 2 ... F t (1) C_{t+1} = C_t F_{t+1} \implies C_t = F_1 F_2 \dots F_t \tag{1} Ct+1=CtFt+1⟹Ct=F1F2...Ft(1)
尽管本文的讨论聚焦于二维参数化运动模型 F t F_t Ft,但我们的系统在理论上可适用于更高维度的线性运动,不过本文暂不对此展开研究。已知原始路径 C t C_t Ct,我们将期望的平滑路径表示为:
P t = C t B t (2) P_t = C_t B_t \tag{2} Pt=CtBt(2)
其中 B t = C t − 1 P t B_t = C_t^{-1} P_t Bt=Ct−1Pt 为更新变换(update transform)------ 将该变换应用于原始相机路径 C t C_t Ct,即可得到最优路径 P t P_t Pt。该变换可被解释为 "稳定化与重定目标变换"(或裁剪变换):在每帧图像中,将其应用于以画面中心为基准的裁剪窗口,便能得到最终的稳定视频。
该优化的目标是找到最优稳定相机路径 P ( t ) P(t) P(t),使如下目标函数最小化:
O ( P ) = w 1 ∥ D ( P ) ∥ 1 + w 2 ∥ D 2 ( P ) ∥ 1 + w 3 ∥ D 3 ( P ) ∥ 1 (3) O(P) = w_1 \| D(P) \|_1 + w_2 \| D^2(P) \|_1 + w_3 \| D^3(P) \|_1 \tag{3} O(P)=w1∥D(P)∥1+w2∥D2(P)∥1+w3∥D3(P)∥1(3)
且满足前文提及的多个约束条件。若不加约束,最优路径将为恒定路径,即对所有 t t t,均有 P t = I P_t = I Pt=I(其中 I I I 为单位矩阵)。
-
最小化 ∥ D ( P ) ∥ 1 \| D(P) \|1 ∥D(P)∥1 :使用前向差分; ∣ D ( P ) ∣ = ∑ t ∣ P t + 1 − P t ∣ = ∑ t ∣ C t + 1 B t + 1 − C t B t ∣ |D(P)| = \sum_t |P{t+1} - P_t| = \sum_t |C_{t+1}B_{t+1} - C_tB_t| ∣D(P)∣=∑t∣Pt+1−Pt∣=∑t∣Ct+1Bt+1−CtBt∣,利用方程 (2)。应用方程 (1) 中 C t C_t Ct 的分解:
∣ D ( P ) ∣ = ∑ t ∣ C t F t + 1 B t + 1 − C t B t ∣ ≤ ∑ t ∣ C t ∣ ∣ F t + 1 B t + 1 − B t ∣ |D(P)| = \sum_t |C_t F_{t+1} B_{t+1} - C_t B_t| \le \sum_t |C_t| |F_{t+1} B_{t+1} - B_t| ∣D(P)∣=t∑∣CtFt+1Bt+1−CtBt∣≤t∑∣Ct∣∣Ft+1Bt+1−Bt∣在 C t C_t Ct 已知的情况下,我们因此寻求最小化残差
∑ t ∣ R t ∣ , 其中 R t : = F t + 1 B t + 1 − B t (4) \sum_t |R_t|, \text{ 其中 } R_t := F_{t+1} B_{t+1} - B_t \tag{4} t∑∣Rt∣, 其中 Rt:=Ft+1Bt+1−Bt(4)对所有 B t B_t Bt 进行求和。在图 2 中,我们可视化了这个残差背后的直觉。当连续对帧 I 2 I_2 I2 应用更新变换 B 2 B_2 B2 和特征变换 F 2 F_2 F2 产生与对帧 I 1 I_1 I1 应用 B 1 B_1 B1 相同的结果(即 R 1 = 0 R_1 = 0 R1=0)时,就实现了常数路径。
-
最小化 ∣ D 2 ( P ) ∣ 1 |D^2(P)|1 ∣D2(P)∣1: 虽然前向差分给出 ∣ D 2 ( P ) ∣ = ∑ t ∣ D P t + 2 − D P t + 1 ∣ = ∑ t ∣ P t + 2 − 2 P t + 1 + P t ∣ |D^2(P)| = \sum_t |D P{t+2} - D P_{t+1}| = \sum_t |P_{t+2} - 2P_{t+1} + P_t| ∣D2(P)∣=∑t∣DPt+2−DPt+1∣=∑t∣Pt+2−2Pt+1+Pt∣,但必须小心,因为我们将误差建模为加性的而不是组合的。因此,我们直接最小化残差的差值:
∣ R t + 1 − R t ∣ = ∣ F t + 2 B t + 2 − ( I + F t + 1 ) B t + 1 + B t ∣ (5) |R_{t+1} - R_t| = |F_{t+2}B_{t+2} - (I + F_{t+1})B_{t+1} + B_t| \tag{5} ∣Rt+1−Rt∣=∣Ft+2Bt+2−(I+Ft+1)Bt+1+Bt∣(5)如图 2 所示。

-
图 2
-
最小化 ∣ D 3 ( P ) ∣ 1 |D^3(P)|1 ∣D3(P)∣1: 类似地,
∣ R t + 2 − 2 R t + 1 + R t ∣ = ∣ F t + 3 B t + 3 − ( I + 2 F t + 2 ) B t + 2 + ( 2 I + F t + 1 ) B t + 1 − B t ∣ (6) |R{t+2} - 2R_{t+1} + R_t| = \\ |F_{t+3}B_{t+3} - (I + 2F_{t+2})B_{t+2} + (2I + F_{t+1})B_{t+1} - B_t| \tag{6} ∣Rt+2−2Rt+1+Rt∣=∣Ft+3Bt+3−(I+2Ft+2)Bt+2+(2I+Ft+1)Bt+1−Bt∣(6) -
关于 B t B_t Bt 最小化: 如前所述,已知帧对变换 F t F_t Ft 和未知更新变换 B t B_t Bt 由线性运动模型表示。例如, F t F_t Ft 可以表示为 6 自由度(DOF)的仿射变换:
F t = A ( x ; p t ) = ( a t b t c t d t ) ( x 1 x 2 ) + ( d x t d y t ) F_t = A(x; p_t) = \begin{pmatrix} a_t & b_t \\ c_t & d_t \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} dx_t \\ dy_t \end{pmatrix} Ft=A(x;pt)=(atctbtdt)(x1x2)+(dxtdyt)其中 p t p_t pt 是参数向量 p t = ( d x t , d y t , a t , b t , c t , d t ) T p_t = (dx_t, dy_t, a_t, b_t, c_t, d_t)^T pt=(dxt,dyt,at,bt,ct,dt)T。通过设置 a t = d t a_t = d_t at=dt 和 b t = − c t b_t = -c_t bt=−ct 可以获得类似的 4 DOF 线性相似变换。
我们要最小化在所有更新变换 B t B_t Bt(由其对应向量 p t p_t pt 参数化)上的方程 (4) 到 (6) 中得出的残差的加权 L1 范数。那么,方程 (4) 中常数路径段的残差变为 ∣ R t ( p ) ∣ = ∣ M ( F t + 1 ) p t + 1 − p t ∣ |R_t(p)| = |M(F_{t+1})p_{t+1} - p_t| ∣Rt(p)∣=∣M(Ft+1)pt+1−pt∣,其中 M ( F t + 1 ) M(F_{t+1}) M(Ft+1) 是以参数形式表示 F t + 1 B t + 1 F_{t+1}B_{t+1} Ft+1Bt+1 矩阵乘法的线性操作。
-
LP 求解: 参数形式中残差 L1 范数的最小化可以通过引入 松弛变量(slack variables) 获得。每个残差将需要引入 N N N 个松弛变量,其中 N N N 是底层参数化的维度,例如在仿射情况下 N = 6 N=6 N=6。对于 n n n 帧,这对应于引入大约 3 n N 3nN 3nN 个松弛变量。具体来说,设 e e e 为 N N N 个正松弛变量的向量,我们从下方和上方限制每个残差,例如对于 ∣ D ( P ) ∣ |D(P)| ∣D(P)∣:
− e ≤ M ( F t + 1 ) p t + 1 − p t ≤ e -e \le M(F_{t+1})p_{t+1} - p_t \le e −e≤M(Ft+1)pt+1−pt≤e且 e ≥ 0 e \ge 0 e≥0。目标是最小化 c T e c^T e cTe,如果 c = 1 c=1 c=1,这对应于 L1 范数的最小化。通过调整 c c c 的权重,我们可以将最小化引向特定参数,例如,我们可以将严格仿射部分的权重设为高于平移部分。这也是必要的,因为平移和仿射部分具有不同的尺度,因此我们对仿射和平移部分使用 100:1 的加权。
使用我们问题的 LP 公式,很容易对最佳相机路径施加约束。回想一下, p t p_t pt 代表更新变换 B t B_t Bt 的参数化,它变换原本位于帧矩形中心的裁剪窗口。通常,我们希望限制 B t B_t Bt 偏离原始路径的程度,以保留原始视频的意图。因此,我们对参数化 p t p_t pt 的仿射部分施加严格界限: 0.9 ≤ a t , d t ≤ 1.1 , − 0.1 ≤ b t , c t ≤ 0.1 , − 0.05 ≤ b t + c t ≤ 0.05 0.9 \le a_t, d_t \le 1.1, -0.1 \le b_t, c_t \le 0.1, -0.05 \le b_t + c_t \le 0.05 0.9≤at,dt≤1.1,−0.1≤bt,ct≤0.1,−0.05≤bt+ct≤0.05,以及 − 0.1 ≤ a t − d t ≤ 0.1 -0.1 \le a_t - d_t \le 0.1 −0.1≤at−dt≤0.1。前两个约束限制了缩放和旋转的变化范围,而后两个通过限制倾斜(skew)和非均匀缩放的量,赋予仿射变换更多的刚性。因此在每种情况下,我们都有上限 (ub) 和下限 (lb),可以写成:
l b ≤ U p t ≤ u b (7) lb \le U p_t \le ub \tag{7} lb≤Upt≤ub(7)
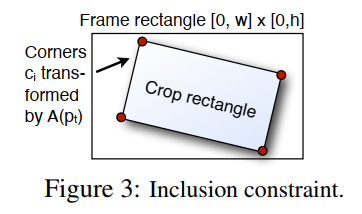
- 图 3
对于由 U U U 指定的 p t p_t pt 上的合适线性组合。为了满足包含约束,我们要求裁剪矩形的 4 个角点 c i = ( c i x , c i y ) , i = 1..4 c_i = (c_i^x, c_i^y), i=1..4 ci=(cix,ciy),i=1..4 必须位于由线性操作 A ( p t ) A(p_t) A(pt) 变换的帧矩形内,如图 3 所示。通常,在我们的框架中建模形式为"凸形状中的变换点"的硬约束是可行的。例如对于 p t p_t pt 的仿射参数化,我们要求:
( 0 0 ) ≤ ( 1 0 c i x c i y 0 0 0 1 0 0 c i x c i y ) ⏟ : = C R i p t ≤ ( w h ) (8) \begin{pmatrix} 0 \\ 0 \end{pmatrix} \le \underbrace{\begin{pmatrix} 1 & 0 & c_i^x & c_i^y & 0 & 0 \\ 0 & 1 & 0 & 0 & c_i^x & c_i^y \end{pmatrix}}_{:=CR_i} p_t \le \begin{pmatrix} w \\ h \end{pmatrix} \tag{8} (00)≤:=CRi (1001cix0ciy00cix0ciy)pt≤(wh)(8)
其中 w w w 和 h h h 是帧矩形的尺寸。
- 算法 1

最佳相机路径的完整 L1 最小化 LP 及约束总结在 算法 1 中。我们在图 4 中展示了从图 10 视频的原始相机路径计算出的最佳路径示例。请注意源自拍摄时行人的 y y y 方向低频跳动是如何被静止相机模型取代的。
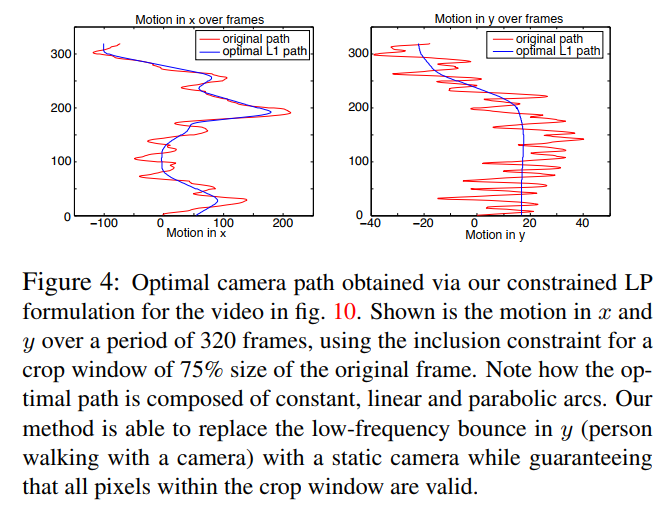
- 图 4
Adding saliency constraints
虽然上述公式对于视频稳像已足够,但我们可以使用修改后的基于特征的公式,执行由硬和软显著性约束自动控制的定向视频稳像。针对显著性度量进行优化对更新变换施加了额外的约束。具体来说,我们要求显著点驻留在裁剪窗口内,这本质上是我们包含约束的逆过程。因此,我们考虑优化更新变换的逆,即应用于每一帧 I t I_t It 中特征集的扭曲(warp)变换 W t W_t Wt,如图 5 所示。我们将 F t F_t Ft 的逆表示为 G t = F t − 1 G_t = F_t^{-1} Gt=Ft−1。我们不是通过 B t B_t Bt 变换裁剪窗口,而是寻求当前特征的变换 W t W_t Wt,使得它们在固定裁剪窗口内的运动仅由常数、线性或抛物线运动组成。实际的更新或稳像变换由 B t = W t − 1 B_t = W_t^{-1} Bt=Wt−1 给出。我们根据图 5 简要推导 D i W t , i = 1..3 D^i W_t, i=1..3 DiWt,i=1..3 的相应目标:
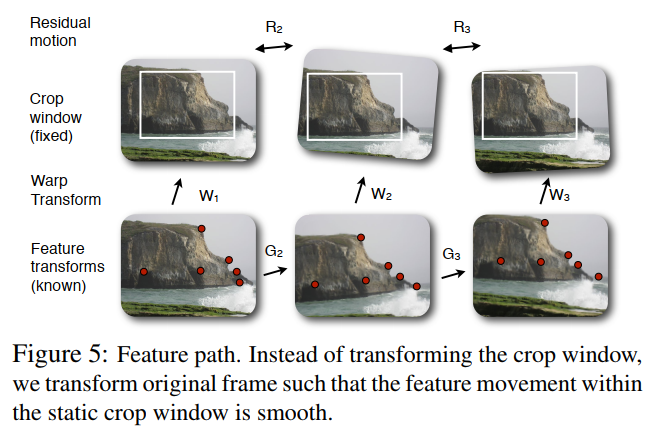
- 图 5
最小化 ∣ D W t ∣ |D W_t| ∣DWt∣: ∣ R t ∣ = ∣ W t + 1 G t + 1 − W t ∣ |R_t| = |W_{t+1}G_{t+1} - W_t| ∣Rt∣=∣Wt+1Gt+1−Wt∣
最小化 ∣ D 2 W t ∣ |D^2 W_t| ∣D2Wt∣: ∣ R t + 1 − R t ∣ = ∣ W t + 2 G t + 2 − W t + 1 ( I + G t + 1 ) + W t ∣ |R_{t+1} - R_t| = |W_{t+2}G_{t+2} - W_{t+1}(I + G_{t+1}) + W_t| ∣Rt+1−Rt∣=∣Wt+2Gt+2−Wt+1(I+Gt+1)+Wt∣
最小化 ∣ D 3 W t ∣ |D^3 W_t| ∣D3Wt∣: ∣ R t + 2 − 2 R t + 1 + R t ∣ = ∣ W t + 3 G t + 3 − W t + 2 ( I + 2 G t + 2 ) + W t + 1 ( 2 I + G t + 1 ) − W t ∣ |R_{t+2} - 2R_{t+1} + R_t| = |W_{t+3}G_{t+3} - W_{t+2}(I + 2G_{t+2}) + W_{t+1}(2I + G_{t+1}) - W_t| ∣Rt+2−2Rt+1+Rt∣=∣Wt+3Gt+3−Wt+2(I+2Gt+2)+Wt+1(2I+Gt+1)−Wt∣
这种特征路径公式的优势在于它处理显著性约束的灵活性。假设我们希望特定点(例如显著性图的模态)或凸区域(例如来自人脸检测器)包含在裁剪窗口内。我们将帧 I t I_t It 中的一组显著点表示为 s i t s_i^t sit。由于我们要估计特征扭曲变换而不是裁剪窗口变换,我们可以对 A ( p t ) A(p_t) A(pt) 变换后的 s i t s_i^t sit 引入单边界限:
( 1 0 s i x s i y 0 0 0 1 0 0 s i x s i y ) p t − ( b x b y ) ≥ ( − ϵ x − ϵ y ) \begin{pmatrix} 1 & 0 & s_i^x & s_i^y & 0 & 0 \\ 0 & 1 & 0 & 0 & s_i^x & s_i^y \end{pmatrix} p_t - \begin{pmatrix} b_x \\ b_y \end{pmatrix} \ge \begin{pmatrix} -\epsilon_x \\ -\epsilon_y \end{pmatrix} (1001six0siy00six0siy)pt−(bxby)≥(−ϵx−ϵy)
其中 ϵ x , ϵ y ≥ 0 \epsilon_x, \epsilon_y \ge 0 ϵx,ϵy≥0。界限 ( b x , b y ) (b_x, b_y) (bx,by) 表示显著点应该距离左上角多远(至少),如图 6 插图所示。对右下角引入类似的约束。选择 b x = c x b_x = c_x bx=cx 和 c y = b y c_y = b_y cy=by 将确保显著点位于裁剪窗口内。对于 b x > c x b_x > c_x bx>cx,显著点可以移动到裁剪矩形的特定区域,例如图 1 中演示的中心。选择 ϵ x , ϵ y = 0 \epsilon_x, \epsilon_y = 0 ϵx,ϵy=0 使其成为硬约束;然而缺点是它可能与帧矩形的包含约束冲突并牺牲路径平滑度。因此,我们选择将 ϵ x , ϵ y \epsilon_x, \epsilon_y ϵx,ϵy 视为新的松弛变量,将其添加到 LP 的目标中。相关权重控制平滑路径和重定向约束之间的权衡。我们在实验中使用了 10 的重定向权重。
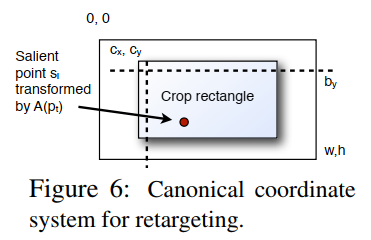
- 图 6
很明显,特征路径公式比相机路径公式更强大,因为它除了邻近和包含约束外,还允许重定向约束。然而,包含约束需要调整,因为裁剪窗口点现在由优化的特征扭曲变换的逆进行变换,使其成为非线性约束。解决方案是要求变换后的帧角点位于裁剪矩形周围的矩形区域内,如图 7 所示,有效地替换包含和邻近约束。
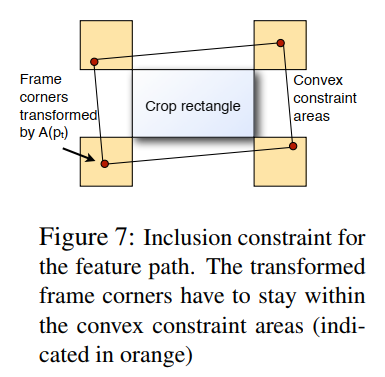
- 图 7
一个有趣的观察是,最佳特征路径的估计可以直接从帧 I t I_t It 中的特征点 f k t f_k^t fkt 实现,即不需要计算 G t G_t Gt。在这种设置下,我们不最小化参数化残差 R ( p t ) R(p_t) R(pt) 的 L1 范数,而是直接最小化特征距离的 L1 范数。 R t R_t Rt 变为:
∣ R t ∣ = ∑ f k : feature matches ∣ W ( p t ) f k t − W ( p t + 1 ) f k t + 1 ∣ 1 |R_t| = \sum_{f_k : \text{feature matches}} |W(p_t)f_k^t - W(p_{t+1})f_k^{t+1}|_1 ∣Rt∣=fk:feature matches∑∣W(pt)fkt−W(pt+1)fkt+1∣1
由于 G t G_t Gt 被计算为满足 G t + 1 f k t = f k t + 1 G_{t+1}f_k^t = f_k^{t+1} Gt+1fkt=fkt+1(在某种度量下),我们注意到先前描述的从特征变换 G t G_t Gt 优化特征扭曲 W t W_t Wt 本质上是对所有特征的误差进行平均,而不是在 L1 意义上选择最好的。我们实现了直接从特征估计最佳路径以供参考,但发现它的好处很小,而且由于其复杂性太慢而无法在实践中使用。
Video Stabilization
我们通过以下步骤执行视频稳像:(1) 估计每帧运动变换 F t F_t Ft,(2) 按照第 2 节所述计算最佳相机路径 P t = C t B t P_t = C_t B_t Pt=CtBt,以及 (3) 通过根据 B t B_t Bt 进行扭曲来稳定视频。
对于运动估计,我们使用金字塔 Lucas-Kanade [12] 跟踪特征。然而,鲁棒性需要良好的异常值剔除。对于动态视频分析,全局异常值剔除是不够的,而相邻视频帧之间的短基线使得基于基础矩阵的异常值剔除不稳定。之前的努力通过 SfM [8] 进行场景的 3D 重建来解决这个问题,除了本身具有稳定性问题外,计算成本也很高。
我们采用局部异常值剔除,将特征离散化为 50 × 50 50 \times 50 50×50 像素的网格,在每个网格单元内应用 RANSAC 来估计平移模型,并仅保留那些与估计模型一致(距离 < 2 像素)的匹配。我们还实现了基于图的分割 [2] 的实时版本,以便对分割区域(而不是网格单元)内的所有特征应用 RANSAC,结果证明稍微优越一些。但是,我们在所有结果中都使用了基于网格的方法,因为它大约快 40%。
随后,我们将几个 2D 线性运动模型(平移、相似和仿射)拟合到跟踪的特征。虽然通过预归一化的正规方程进行的 L2 最小化在大多数情况下表现良好,但在突然几乎完全遮挡的情况下我们注意到了不稳定性。因此,我们通过 LP 求解器 在 L1 范数中执行拟合,这通过自动执行特征选择增加了这些情况下的稳定性。据我们所知,这是 L1 最小化在相机运动估计中的新应用,并给出了令人惊讶的稳健结果。
一旦相机路径被计算为一组线性运动模型,我们就根据我们的 L1 优化框架拟合最佳相机路径,并遵守第 2 节中描述的邻近和包含约束。一个关键问题是如何在目标方程 (3) 中选择权重 w 1 − w 3 w_1 - w_3 w1−w3 我们在图 8 中探索了合成路径的不同加权。如果仅最小化三个导数约束中的一个,很明显原始路径被近似为不连续的常数路径(图 8a)、带有急动的线性路径(图 8b)或平滑抛物线但始终存在非零运动(图 8c)。通过同时最小化所有三个目标,可以传达更愉悦的观看体验。虽然权重的绝对值不是太重要,但我们发现消除急动是最重要的,当 w 3 w_3 w3 选择为比 w 1 w_1 w1 和 w 2 w_2 w2 大一个数量级时可以实现这一点。
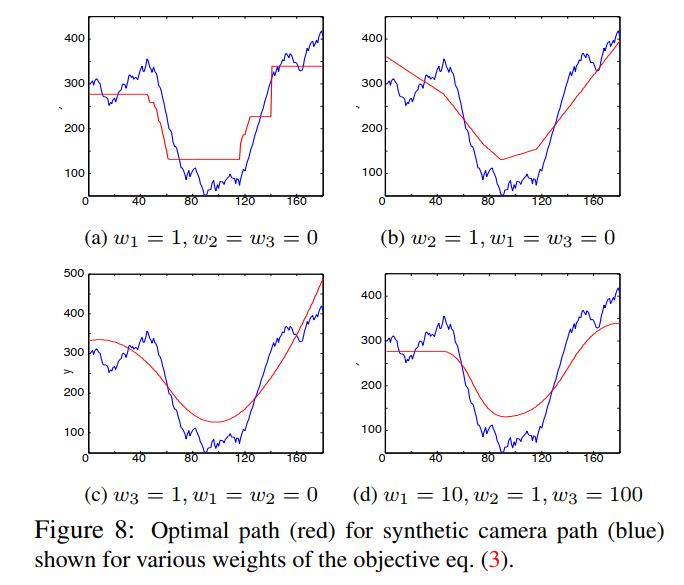
- 图 8
底层运动模型的选择对稳定的视频有深远的影响。使用仿射变换而不是相似变换具有两个额外自由度的好处,但会受到偏斜(skew)误差的影响,从而导致非刚性效应(正如 [8] 所观察到的)。因此,我们使用相似变换来构建我们的最佳路径。然而,相似变换(如仿射变换)无法模拟非线性帧间运动或卷帘快门(rolling shutter)效应,从而导致明显的残留晃动(wobble),我们将在接下来解决这个问题。
残余运动(晃动和卷帘快门)抑制 : 为了精确模拟彻底消除抖动所需的帧间运动,需要比相似变换具有更高 DOF 的运动模型,例如单应性矩阵(homographies)。然而,即使采用了异常值剔除,更高的 DOF 也容易过拟合。因此,人们可以在几帧内实现良好的配准,但它们的组合开始迅速变得不稳定,例如单应性矩阵开始遭受过度的偏斜和透视变形。我们建议一种鲁棒的混合方法,最初使用相似变换(用于帧变换) F t : = S t F_t := S_t Ft:=St 来构建最佳相机路径,从而确保所有帧的刚性。然而,我们仅对每 k = 30 k=30 k=30 个关键帧应用计算出的刚性相机路径。对于中间帧,我们使用更高维的单应性矩阵 F t : = H t F_t := H_t Ft:=Ht 来解释未对齐。如图 9 所示,我们将两个最佳(且刚性)相邻相机变换 P 1 − 1 P 2 P_1^{-1}P_2 P1−1P2 之间的差异分解为已知的估计相似部分 S 2 S_2 S2 和平滑残余运动 T 2 T_2 T2,即 P 1 − 1 P 2 = S 2 T 2 P_1^{-1}P_2 = S_2 T_2 P1−1P2=S2T2( T 2 = 0 T_2 = 0 T2=0 意味着静止相机)。然后我们用更高维的单应性矩阵 H 2 H_2 H2 替换低维相似 S 2 S_2 S2,得到 P 1 − 1 P 2 : = H 2 T 2 P_1^{-1}P_2 := H_2 T_2 P1−1P2:=H2T2。对于每个中间帧,我们从其上一个和下一个关键帧开始连接这些替换。这实际上导致每个像素有两个采样位置 q 1 , q 2 q_1, q_2 q1,q2(在图 9 中用红色和绿色表示),在我们的实验中平均误差约为 2-5 像素。我们在此时两个位置之间使用线性混合来确定帧的逐像素扭曲。
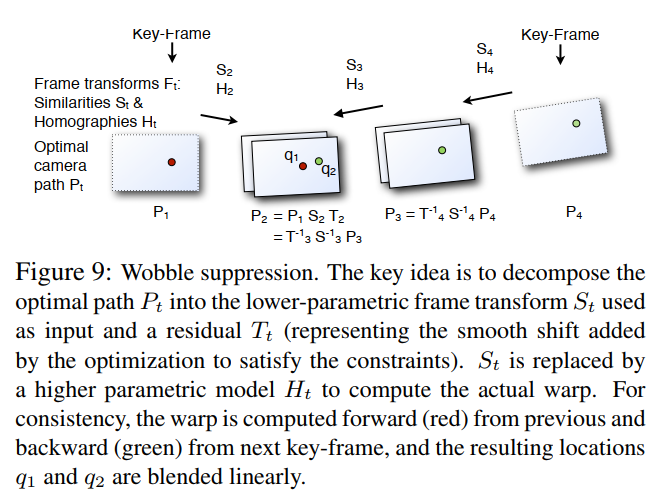
- 图 9
Video Retargeting
视频重定向旨在改变视频的宽高比,同时保留显著和视觉上突出的区域。最近,很多焦点集中在"内容感知"方法上,这些方法要么基于显著性图 [14] 扭曲帧,要么以时间相干的方式移除和复制非显著接缝(seams)[11, 4]。
在 2.2 节中,我们展示了如何指导裁剪窗口包含显著点,而不必牺牲结果路径的平滑度和稳定性。另一方面,如果输入视频已经是稳定的,即 C ( t ) C(t) C(t) 是平滑的,我们可以通过避开每帧变换 F t F_t Ft 的估计来显式地建模此属性,并强制其为恒等变换 F t = I , ∀ t F_t = I, \forall t Ft=I,∀t。这允许我们仅基于显著性和包含约束来操纵裁剪窗口,通过自动"摇摄扫描(pan-and-scan)"实现视频重定向。简单地说,当假设输入视频稳定时,视频重定向是我们基于显著性优化的特例。与 Liu 和 Gleicher [7] 的工作相比,我们的相机路径不限于单个摇摄,允许更多的自由度(例如微妙的变焦)和对复杂运动模式的适应。
虽然存在多种显著性度量,但我们主要关注运动驱动的显著性。我们的动机是假设观众将注意力指向移动的前景对象,这是在限制范围内的合理假设。使用基础矩阵约束和 KLT 特征轨迹上的聚类,我们获得前景显著性特征,如图 12 所示,然后将其用作约束,如 2.2 节所述。