目录
[二、es的对应 C++ 数据类型(两种常见写法)](#二、es的对应 C++ 数据类型(两种常见写法))
[写法 1:使用struct自定义边类型(兼容性更好,低版本 C++ 也支持)](#写法 1:使用struct自定义边类型(兼容性更好,低版本 C++ 也支持))
[写法 2:使用tuple元组(简洁,依赖 C++11 及以上)](#写法 2:使用tuple元组(简洁,依赖 C++11 及以上))
[核心原因:Dijkstra 算法的"局限性"------ 无法正确处理负权边(可处理非负权边)](#核心原因:Dijkstra 算法的“局限性”—— 无法正确处理负权边(可处理非负权边))
三,例题训练(本类题用得少,无论是比赛还是实际开发都少,只做思维锻炼即可)
注:本文所有题目均来自蓝桥杯官网公开真题,仅做算法学习,代码皆由本人做出来并附上解析!
一,前言
1.几种常见的最短路算法:
(1)dijkstra单源最短路,仅适用于正权图,时间复杂度o(nlogN)。
(2)Floyd全源最短路,仅适用于正权图,o(n^3)。
(3)还有一种常见的单源最短路算法,叫bellmanford算法,它可以计算负权图的单源最短路,且可以判断负环,但是时间复杂度较高,o(nm)。
Bellmanford算法的思路:松弛:用这条边去更新源点到出点的最短路径。用每条边去做松弛操作,进行n-1轮松弛,因为在n个点的图中一条路径最多由n-1条边组成,如果n-1轮松弛之后还能松弛,就说明存在负权环,否则就可以得到单源最短路。
因为在走最短路径时,遇到了负权环它的路径和就会不断减少,永远都会比之前少,直到负无穷
2.代码:
cpp
ll h[N];//h[N]表示源点0到x的最短距离,通过bellmanford计算
bool bellmanford()
{
//初始化h[]为正无穷
for (int i = 1; i <= n; i++)h[i] = inf;
//h[1]=0这个可以忽略
h[0] = 0;
//一共n个点,所以松弛n-1次,i仅用于计数
for (int i = 1; i < n; i++)
{
//枚举所有边,尝试用这条边去松弛点x
for (const auto& [x, y, w] : es)//es:vector
{
if (h[x] == inf)continue;
//如果可以通过这条边松弛
if (h[x] + w < h[y])
{
h[y] = h[x] + w;
}
}
}
//判断是否存在负权环
for(const auto &[x,y,w]:es)
{
if (h[x] == inf)continue;
//如果还有边可以松弛,那么说明存在负环(边权之和为负)返回false
if (h[x] + w < h[y])return false;
}
//不存在负环,返回true
return true;
}3.代码简单介绍
一、es的核心定义
es 是一个存储图中所有边的容器(这里明确是vector向量容器) ,并且每一条边都包含了三个核心信息:x(边的起点)、y(边的终点)、w(这条边的权重,可正可负,对应 Bellman-Ford 算法的场景)。
简单来说,es就是整个图的 "边集合",Bellman-Ford 算法的核心就是通过枚举这个集合中的所有边来进行松弛操作。
二、es的对应 C++ 数据类型(两种常见写法)
代码中使用了 C++17 及以上支持的结构化绑定(const auto& [x, y, w] : es) ,对应es的两种常见合法定义:
写法 1:使用struct自定义边类型(兼容性更好,低版本 C++ 也支持)
cpp
// 1. 先定义边的结构体
struct Edge {
int x; // 起点
int y; // 终点
long long w; // 权重(用long long避免溢出,对应h[N]的ll类型)
};
// 2. 定义es容器(存储所有边)
vector<Edge> es;写法 2:使用tuple元组(简洁,依赖 C++11 及以上)
cpp
// 直接定义存储三元组的vector,顺序对应x、y、w
// 注意:tuple的元素类型要和x、y、w匹配,ll对应long long
vector<tuple<int, int, long long>> es;三,为什么之枚举n-1次
Bellman-Ford 算法的n-1次枚举,本质是按 "边数" 逐层推进,逐步确定源点到各节点的最短路径,可以理解为 "迭代解锁":
- 第 1 次枚举所有边:只能确定 "源点直接可达" 的节点(即最短路径仅包含 1 条边的节点)的最短距离,这些节点的最短路径被 "解锁",无法确定需要更多边的节点;
- 第 2 次枚举所有边:基于第 1 次的结果,能确定 "最短路径包含最多 2 条边" 的节点的最短距离,进一步解锁更多节点;
- ...... 以此类推 :每多枚举 1 次,就能把最短路径的边数上限提升 1,直到第
k次枚举,能确定最短路径包含最多k条边的节点; - 第 n-1 次枚举所有边 :此时已经覆盖了 "最短路径包含最多
n-1条边" 的所有可能情况,所有节点的最短距离都已经被最终确定,后续再枚举边也无法再更新(松弛)任何节点的最短距离了。
这些路径都是从源点开始的。
二,Johnson算法介绍
1.johnson算法:大致分为以下3步
1,设置超级源点,用bellmanford求单源最短路(所有点到超级源点的最短距离)得到"势能"h[],并且判断负环
2,在势能帮助下重新设置每条边的权重
3,跑n次dijkstra算法计算出所有点的单源最短路,即得到了全源最短路
2.re-weight
(图片来自蓝桥杯官网)
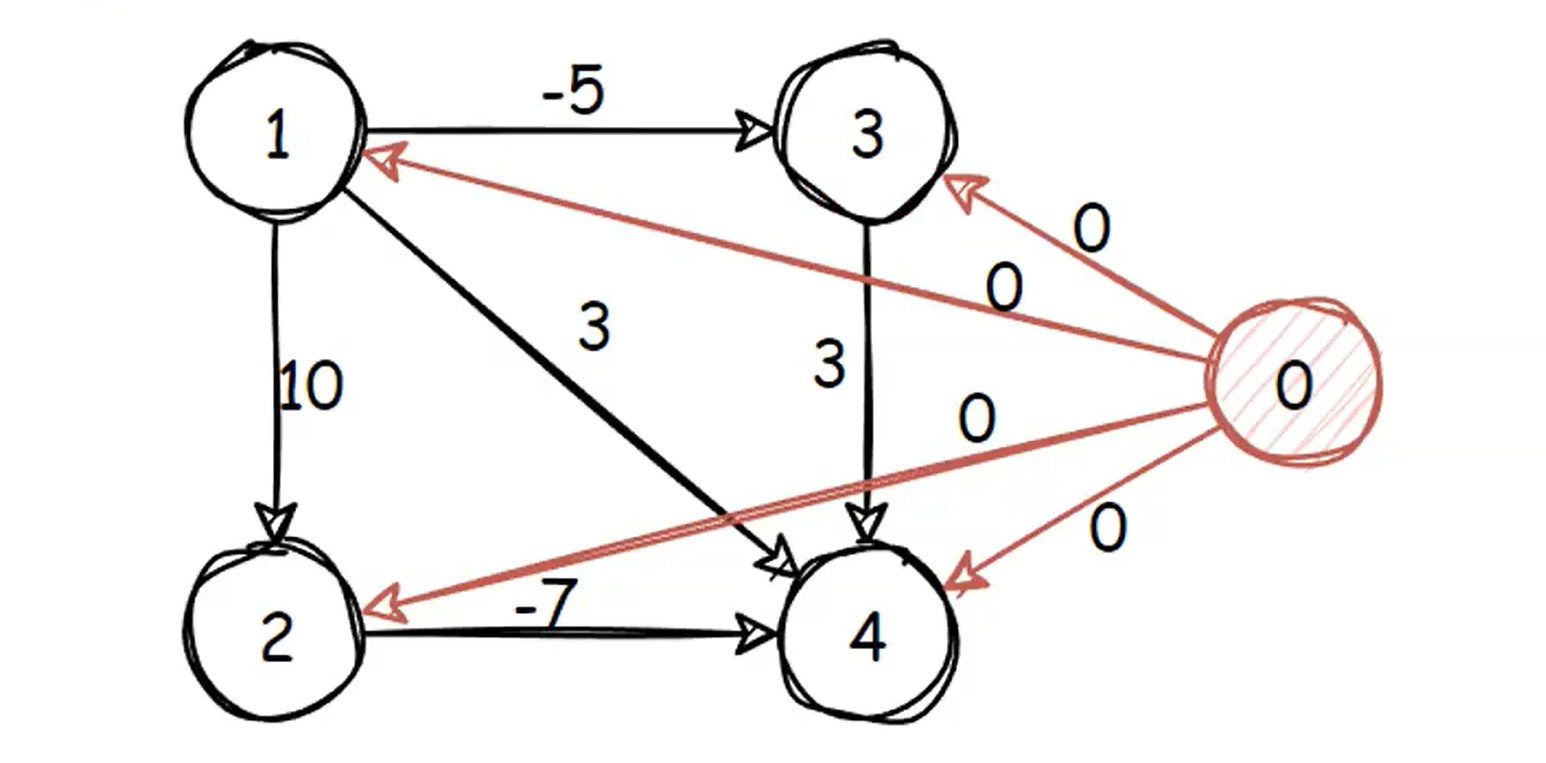
RE-weight顾名思义就是重新调整每条边的权重,对于一个图,我们先建立一个"super source node(超级源点)",用0号节点表示,并且将其与所有节点链接起来,边权为0。
接下来用bellmanford算法计算出超级源点的单源距离最短路,这个是很简单的(吗?)
由图,图中存在负权,但是注意,图中有负权并不一定代表图中有负环!
负环是个啥?
负环特指有向图中一个满足"边权之和为负数"的环。
会导致:最短路径不存在------ 如果从源点出发,能到达一个负环,那么可以无限次绕这个负环循环 。每绕一圈,路径的总权值就会减少一次,最终路径长度会趋近于 负无穷。
但是,有负权会影响什么呢?
核心原因:Dijkstra 算法的"局限性"------ 无法正确处理负权边(可处理非负权边)
这是重赋权(将边权转为非负)的根本原因:
- Dijkstra 算法的核心缺陷 :Dijkstra 算法基于 "贪心策略",它假设一旦某个节点被从优先队列中取出并标记为已访问(vis[x]==true),就已经找到了从源点到该节点的最短路径,后续无需再更新该节点的距离。
- 负权边会打破这个假设:如果图中存在负权边,当一个节点被标记为已访问后,后续可能会通过一条包含负权边的路径,找到到该节点的更短距离,此时 Dijkstra 算法无法回溯更新,会得出错误的最短路径结果。
- 非负权边是 Dijkstra 算法的安全保障:当所有边权都是非负数时,贪心策略完全成立 ------ 被取出的节点的最短距离已经确定,不会被后续路径更新,算法能够正确求解,且效率极高。
简单来说:我们需要 Dijkstra 算法的高效性,但它无法处理负权边,因此需要将负权边转为非负权边,让 Dijkstra 算法可以安全运行。
所以要先更新所有边权变为非负数,之后才能求出单源最短路。
之后,假如存在负环,现在我们就得到了一个h[]数组,接下来我们令每条边的权重w(u,v)=w(u,v)+h[u]-h[v]
这样一定可以使得所有边权为正权,假如w(u,v)<0,那么必然有h[u]+w(u,v)>=h[v],于是有:w(u,v)+h[u]-h[v]>=0
在此基础上去对每一个点跑一遍dijkstra算法,即可求得对于每一个点的单源最短路
如何理解呢?
由图中的w(1,3)=-5,h[1]=0,h[3]=-5(由路径0-->1-->3可得)。
对w(1,3)进行操作:w(1,3)=w(1,3)+h[1]-h[3]=-5+0+5=0,成功变为非负数了。
求出来的这个距离叫d(u,v),实际上是进行了偏移之后的,要还原为真实的距离还要令:f(u,v)=d(u,v)-h[u]+h[v]
h他不是d,是势能而不是实际距离,例如:
假如有一条路径:u->x1->x2->......->xk->v,那么就有:d(u,v)=[w(u,x1)+h[u]-h[x1]](就是d(u,x1))+......+d(xk,v)
经变换可以得到:d(u,v)=(w(u,x1)+w(x1,x2)+......+w(xk,v))+h[u]-h[v]
即:d(u,v)=f(u,v)+h[u]-h[v],f(u,v)为u,v的真实距离
由此可见,h只与起始点,终点有关,类比于物理学的重力势能!
所以真实距离是我们计算出的d(u,v)-h[u]+h[v],这个真实距离可能是负数,如果要判断两点不存在路径的话,应该判断d而不是f!若不存在路径,则对应的d应该是inf(无穷)。
三,例题训练(本类题用得少,无论是比赛还是实际开发都少,只做思维锻炼即可)
蓝桥杯官网------小e的公路
问题描述
有一座城市非常特殊,所有道路都是单行道,并且每条道路的距离可能是负数。在该市有 n 个景点,m 条道路,请问对于每个景点,它到所有景点的最短距离与编号的乘积之和是多少?
输入描述
第一行输入两个整数 n, m (1 ≤ n ≤ 10^3, 1 ≤ m ≤ 2 × 10^3)。接下来 m 行,每行输入三个整数 u, v, w (1 ≤ u, v ≤ n, -10^9 ≤ w ≤ 10^9),表示存在一条从 u 到 v 的距离为 w 的道路。
输出描述
输出共 n 行,第 i 行 ansi=∑ j=1nj×dis[i][j]。
dis[u][v] 表示 u 到 v 的最短距离,如果无法到达则认为距离是 10^9。
如果图中存在负权环,则只输出一行 −1。
样例输入1
6 8
1 2 4
2 6 -10
2 4 7
2 5 10
2 3 -2
3 6 -3
5 3 4
6 7 9样例输出1
92
1000000012
11999999982
17000000000
7000000018
15000000000样例输入2
6 8
1 2 4
2 6 -10
2 1 -7
2 5 10
2 3 -2
3 6 -3
5 3 4
6 7 9样例输出2
-1代码详解
cpp
#include <iostream>
#include<queue>
#include<bitset>
#include<vector>
using namespace std;
using ll=long long;
const int N=3e3+9;
const ll inf=1e9;//为什么设置为更大的数不行???????试了我半天
ll h[N],dis[N][N];//分别求势能,dis[i][j]表示i-->j的实际距离
int n,m;
struct edge
{
ll u,v,w;
};
vector<edge>es;
struct Node
{
ll v,w;
//重载<,使得优先队列为小根堆
bool operator<(const Node &u)const
{
return w==u.w?v<u.v:w>u.w;//按照w降序
}
};
vector<Node>g[N];
bool bellmanford()
{
//初始化;
for(int i=1;i<=n;i++) h[i]=inf;
h[0]=0;
//此时有n+1个点,所以松弛n次:
for(int i=1;i<=n;i++)
{
for(const auto &[u,v,w]:es)
{
//跳过无法从源点达到的
if(h[u]==inf) continue;
if(h[u]+w<h[v]) h[v]=h[u]+w;
}
}
//判断负环;
for(const auto &[u,v,w]:es)
{
if(h[u]==inf) continue;
//假设还能松弛,说明存在负环
if(h[u]+w<h[v]) return false;
}
return true;
}
void dijkstra(ll st)
{
priority_queue<Node>pq;
bitset<N>vis;
static ll d[N];//d不能是全局变量,因为每次st(原点)都不同
//初始化距离
for(int i=1;i<=n;i++) d[i]=inf;
pq.push({st,d[st]=0});
while(pq.size())
{
ll v=pq.top().v;
//要先出队
pq.pop();
//ll w=pq.top().w;
if(vis[v]) continue;
vis[v]=true;
//pq.pop();
for(const auto &[y,dw]:g[v])
{
if(d[v]+dw<d[y]) d[y]=d[v]+dw;
pq.push({y,d[y]});
}
}
//求最短距离(还原真实距离)
for(int i=1;i<=n;i++)
{
if(d[i]==inf) dis[st][i]=d[i];
else dis[st][i]=d[i]-h[st]+h[i];
}
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
ll u,v,w;cin>>u>>v>>w;
es.push_back({u,v,w});//bellmanford
g[u].push_back({v,w});//dijkstra
}
//先建立超级源点,之后再跑bellmanford求出势能
for(int i=1;i<=n;i++) es.push_back({0,i,0});//表示从超级源点到i点的距离都是0
//判断负环:
if(!bellmanford())
{
cout<<-1<<endl;
return;//程序终止
}
//此时求出了势能h
//重新设置边权(在领接表中)
for(int x=1;x<=n;x++)
{
for(auto &[y,w]:g[x]) w=w+h[x]-h[y];
}
//跑n次dijkstra,求出每个点的单源最短路(即所有点的全源最短路)
for(int i=1;i<=n;i++) dijkstra(i);
//得出最终距离:
for(int i=1;i<=n;i++)
{
ll ans=0;
for(int j=1;j<=n;j++) ans += 1ll * j * dis[i][j];
cout<<ans<<endl;
}
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
solve();
return 0;
}