参考:https://blog.csdn.net/jteng/article/details/49590069
目录
[1.1 图的表示](#1.1 图的表示)
[1.2 相似度图的构造方法](#1.2 相似度图的构造方法)
[1.3 图的Laplacian矩阵](#1.3 图的Laplacian矩阵)
[2.1 最小割准则(Min-cut)](#2.1 最小割准则(Min-cut))
[2.2 均衡分割策略:RatioCut 与 Normalized Cut](#2.2 均衡分割策略:RatioCut 与 Normalized Cut)
[2.3 数学求解:拉普拉斯矩阵与松弛化](#2.3 数学求解:拉普拉斯矩阵与松弛化)
[2.3.1 RatioCut 的推导与求解](#2.3.1 RatioCut 的推导与求解)
[2.3.2 多聚类扩展](#2.3.2 多聚类扩展)
[2.3.3 Normalized Cut 的求解差异](#2.3.3 Normalized Cut 的求解差异)
[3. 谱聚类算法标准化流程](#3. 谱聚类算法标准化流程)
[4. 算法总结与性能评估](#4. 算法总结与性能评估)
[4.1 核心优势](#4.1 核心优势)
[4.2 局限性与挑战](#4.2 局限性与挑战)
谱聚类将数据的划分转化为对图的分割,是一种基于图论的聚类方法,其直观理解为根据图内点的相似度将图分为多个子图,使子图内部的点相似度最高,子图之间点的相似度最低。
1.图论的基础
1.1 图的表示
三个关键组成部分:图本身、邻接矩阵 W 和 度矩阵 D
例子:假设我们有4个人:Alice, Bob, Carol, David。我们用一张图来表示他们之间的好友关系,关系紧密程度(权重)用数字表示。
1)图的定义 。
G: 这就是我们所要描述的整个图,它包含了所有顶点(人)和边(好友关系)。
V(顶点集合vertex): 图中所有顶点的集合。
E(边集合edge): 图中所有连接的集合。
无向图:顾名思义,就是没有方向的图。关系是双向的、对等的,没有"谁指向谁"的区别。
2)邻接矩阵 W。
描述图中顶点之间的连接关系(可以理解为权重)。是一个 n×n的方阵(n是顶点数), 表示顶点
和顶点
之间的边的权值。
规则:
: 权值是非负的。
: 如果两点之间没有边直接相连,则权值为0。
w : 因为是无向图,矩阵是对称的
在例子中:
假设好友关系权重如下:
-
Alice和Bob很熟,权重 w12=3
-
Alice和Carol是普通朋友,权重 w13=1
-
Bob和David是朋友,权重 w24=2
-
Carol和David是朋友,权重 w34=2
-
Alice和David不是朋友,Bob和Carol也不是朋友。
那么,邻接矩阵 W如下所示:
3)度 与度矩阵 D。
"度"衡量的是一个顶点与外部世界的"总连接强度"。度 表示顶点
的度,是其所有连接边的权值之和。
在例子中:
(Alice的度) = w12+w13+w14=3+1+0=4
度矩阵是一个对角矩阵,只有对角线上的元素有非零值,这些值就是各个顶点的度 。
在例子中,度矩阵 D为:
4)总结
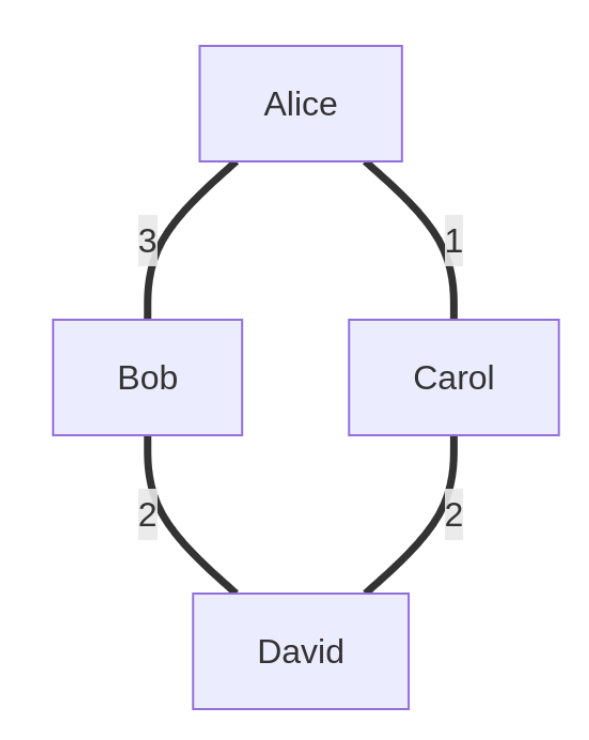
图 (G): 就是上面这个关系图,包含了4个顶点和4条边
1.2 相似度图的构造方法
目的 :给定一堆数据点 ,我们要构建一个图
。这个图用来描述数据点之间的局部近邻关系。边的权重(相似度)越高,表示两个点越相似。
三种构造相似度图的方法:
方法一:ε-近邻图
- 核心思想 :设定一个距离阈值ε。如果两个点之间的距离小于ε,则连接两点。重点在于参数 ε 的选择。且对参数ε非常敏感。
方法二:k-近邻图
-
核心思想 :不为所有点设定一个固定的距离阈值,而是为每个点单独寻找其最接近的k个点作为邻居。这样,每个点都保证有k个邻居。
-
"非相互性"问题与解决策略:
-
问题 :近邻关系不一定是相互的。
是
的k近邻,并不意味着
的k近邻。
-
策略: 采用 "或" 或 "与" 的方法。区别在于连接条件不同,一个是
是
的k近邻或
的k近邻即可,一个是同时满足。
-
优点 是可以自适应不同密度的数据集,缺点是要选择参数 k
方法三:全连接图
-
核心思想 :最简单粗暴的方法------连接所有点对。每个点都和其余所有n-1个点相连。
-
关键 :既然全都连接了,那么边的权重(相似度)就变得至关重要。权重函数需要能够很好地度量相似度,并且对于不相似的点对,权重应该非常小(接近零)。
-
常用的相似性函数:高斯核函数(也称为径向基函数,RBF)
-
-
参数
控制权重随距离衰减的速度,参数越小衰减越快。
在实际应用中,**k-近邻图(通常采用"或"的策略)** 是最常用的方法,因为它在实用性和效果之间取得了很好的平衡。
1.3 图的Laplacian矩阵
在谱聚类中,拉普拉斯矩阵 L=D−W ,这个矩阵蕴含了图的分割信息,是谱聚类算法能够工作的核心。其中D和W就是上文定义的图的度矩阵和邻接矩阵。
2.谱聚类算法
谱聚类算法(Spectral Clustering)的本质是将聚类任务转化为图论中的最优分割问题。首先将所有的样本点连接成图,然后将图分割成不同的子图,使得不同子图之间的连接权值最小。
2.1 最小割准则(Min-cut)
首先,将所有样本点映射为图中的顶点,样本间的相似度作为边的权重。聚类的目标是将图划分为 k 个互不相交的子图 ,并使得各子图之间的连接权值总和达到最小。 定义子图 A 与其补集 Aˉ 之间的连接权值为:
最优分割即最小化以下目标函数:
**问题:**传统的最小割准则往往会产生"孤立点"现象,即算法倾向于切下极少数的点以换取最小的权值和,导致分割结果极度不均衡。
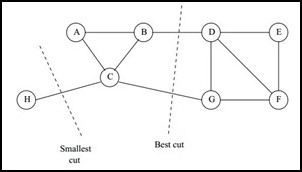
2.2 均衡分割策略:RatioCut 与 Normalized Cut
解决该问题的有效办法是让每个子图都有合理的大小,子图大小的度量方式不同就会得出不同的最小分割问题,常用的两种方法是RaioCut和Normalized Cut
1. RatioCut :以子图内节点的数量 作为规模度量,旨在平衡各簇的样本规模。
2. Normalized Cut (Ncut) :以子图内节点的度之和(Volume) 作为度量,更看重簇内连接的紧密程度。
其中,。通过将子图大小作为分母,强制约束各子图不能过小。
2.3 数学求解:拉普拉斯矩阵与松弛化
2.3.1 RatioCut 的推导与求解
以二聚类为例,引入示性向量,其元素定义如下:
结合图的拉普拉斯矩阵(Laplacian Matrix) L=D−W,利用二次型性质可以推导出:
由于 为常数,最小化 RatioCut 等价于最小化
。
松弛化处理: 寻找最优示性向量是一个 NP-hard 的离散优化问题。通过松弛化 ,允许 f 取任意实数,并加上约束 和
。据 Rayleigh-Ritz 定理 ,该问题的最优解即为矩阵 L 的第二小特征值对应的特征向量。
2.3.2 多聚类扩展
对于 k 聚类,我们定义 k 个正交的示性向量构成矩阵,目标函数转化为:
其解为 的前
个最小特征值对应的特征向量所组成的矩阵。
2.3.3 Normalized Cut 的求解差异
Ncut 的推导逻辑相似,但其松弛化后的优化问题转变为广义特征值问题:
此时,需要求解的是 相对于度矩阵
的前
个广义特征向量。
3. 谱聚类算法标准化流程
基于图分割理论,标准谱聚类算法可以总结为以下四个步骤:
-
Step 1:构建相似度图。将每个样本看做图的顶点,构造无向加权图及其邻接矩阵 W。
-
Step 2:计算矩阵算子。推导度矩阵 D 以及拉普拉斯矩阵 L。
-
Step 3:谱分解(特征提取)。根据 RatioCut 或 Ncut 准则,计算 L 的前 k 个最小特征值对应的特征向量。
-
Step 4:空间重构与聚类 。将提取出的 k 个特征向量按列组成矩阵 Y。将 Y 的每一行视作原始样本在低维空间中的新坐标,然后利用 K-means 算法完成最终聚类。
4. 算法总结与性能评估
谱聚类的本质是一种非线性降维技术。它利用谱分解将数据映射到低维空间,使原始非线性可分的数据在新空间中变得线性可分。最后再使用k-means聚类就可以得到比较好的聚类效果。
4.1 核心优势
-
适应性强:能够处理任意形状(如环形、流形)的数据分布。
-
全局最优倾向:通过特征分解避免了 K-means 易陷入局部最优的缺陷。
4.2 局限性与挑战
-
近似误差:松弛化过程是对原问题的近似,在某些边界条件下可能导致聚类结果不稳定。
-
参数敏感性:相似度矩阵构造中的尺度参数(如高斯核的 σ)对结果影响显著。
-
计算复杂度:对于超大规模数据集,特征值分解的计算开销巨大。
-
均衡性偏见:谱聚类天生偏向于生成规模均衡的簇,对于各簇样本数量差异巨大的场景(如异常检测),其表现可能不如预期。