书籍:Matlab实用教程
因为外出,使用笔记本,没有安装matlab
电脑信息:
处理器 Intel® Core™ i7-7500U CPU @ 2.70GHz 2.90 GHz
系统类型:
系统类型 64 位操作系统, 基于 x64 的处理器
版本 Windows 10 家庭中文版
版本号 22H2
开始时使用在线工具:
https://www.cainiaojc.com/tool/octave/
1、不支持sym
2、不支持状态方程模型创建命令
3、很慢
改使用在线工具:
支持状态方程模型创建命令
也不支持sym
有时候连接不上。
直接安装octave
1、下载文件
2、解压
下载下来的octave-10.3.0-w64.zip,点击解压
octave-10.3.0-w64
3、找到octave-launch.exe

4、使用
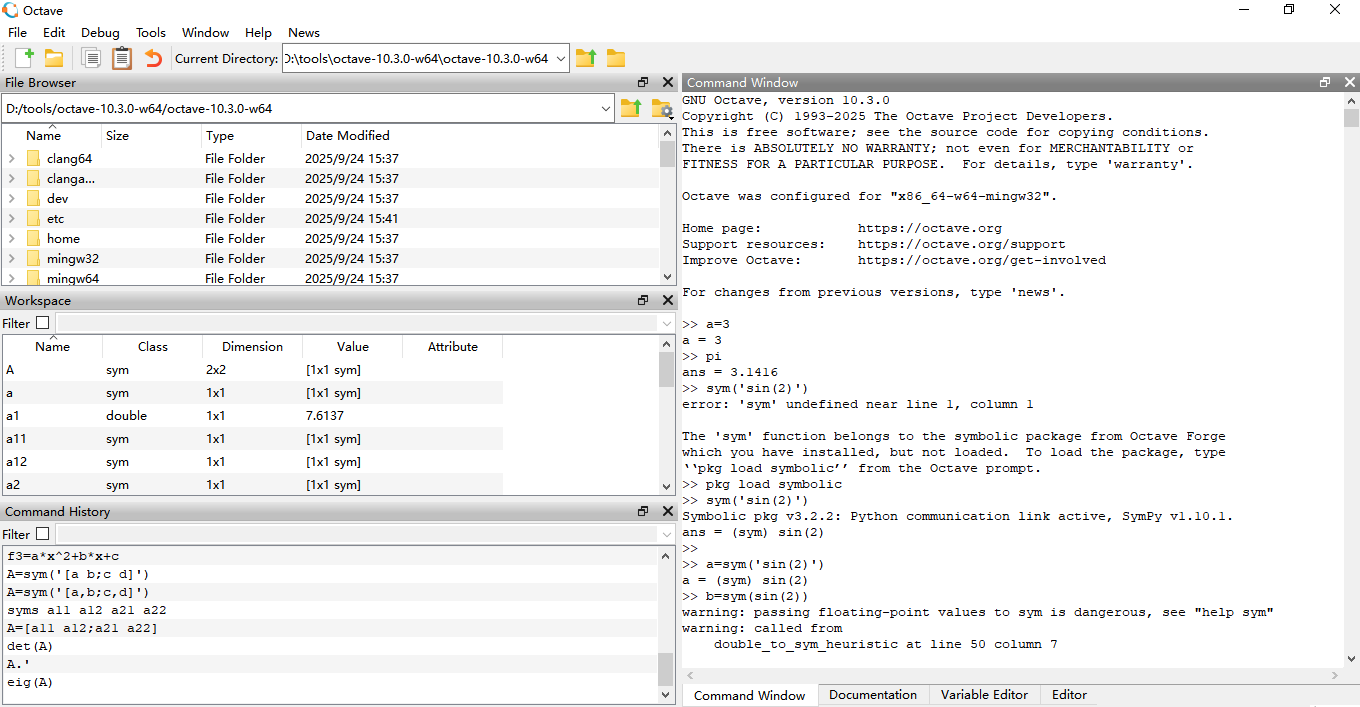
与matalb差不多
使用pkg load symbolic 加载后,也可以使用sym
具体上跟matlab还是有点区别。
第3章 MATLAB 的符号计算
3.1 符号表达式的建立
3.1.1 创建符号常量
>> a=sym('sin(2)')
a = (sym) sin(2)
>> a1=2*sqrt(5)+pi
a1 = 7.6137
>> a2=sym('2*sqrt(5)+pi')
a2 = (sym)
___
pi + 2*\/ 5
>>3.1.2 创建符号变量和表达式
広a31 = (sym) 0
>> sym('x','real')
ans = (sym) x
>> sym('y','real')
ans = (sym) y
>> z=sym('x+iy')
z = (sym) iy + x
>> real(z)
ans = (sym) re(iy) + re(x)
>> f1=sym('a*x^2+b*x+c')
f1 = (sym)
2
a*x + b*x + c
>> syms a b c x
>> f2=a*x^2+b*x+c
f2 = (sym)
2
a*x + b*x + c
>> f3=a*x^2b*x+c
^
>> f3=a*x^2+b*x+c
f3 = (sym)
2
a*x + b*x + c3.1.3 符号矩阵
>> A=sym('[a,b;c,d]')
error: Python exception: SympifyError: Sympify of expression 'could not parse '[a,
b;c,d]'' failed, because of exception being raised:
SyntaxError: invalid syntax (<string>, line 1)
occurred at line 1 of the Python code block:
return S("[a,b;c,d]", rational=True)
error: called from
pycall_sympy__ at line 179 column 7
sym at line 489 column 9
>> syms a11 a12 a21 a22
>> A=[a11 a12;a21 a22]
A = (sym 2x2 matrix)
[a11 a12]
[ ]
[a21 a22]3.2 符号表达式的代数运算
3.2.1 符号表达式的代数运算
>> syms a11 a12 a21 a22
>> A=[a11 a12;a21 a22]
A = (sym 2x2 matrix)
[a11 a12]
[ ]
[a21 a22]
>> det(A)
ans = (sym) a11*a22 - a12*a21
>> A.'
ans = (sym 2x2 matrix)
[a11 a21]
[ ]
[a12 a22]
>> eig(A)
ans = (sym 2x1 matrix)
[ _____________________________________]
[ / 2 2 ]
[a11 a22 \/ a11 - 2*a11*a22 + 4*a12*a21 + a22 ]
[--- + --- - ----------------------------------------]
[ 2 2 2 ]
[ ]
[ _____________________________________]
[ / 2 2 ]
[a11 a22 \/ a11 - 2*a11*a22 + 4*a12*a21 + a22 ]
[--- + --- + ----------------------------------------]
[ 2 2 2 ]
>> f=sym('2*x^2+3*x+4')
f = (sym)
2
2*x + 3*x + 4
>> g=sym('5*x+6')
g = (sym) 5*x + 6
>> f*g
ans = (sym)
/ 2 \
(5*x + 6)*\2*x + 3*x + 4/3.2.2 符号数值任意精度控制和运算
>> a=sym('2*sqrt(5)+pi')
a = (sym)
___
pi + 2*\/ 5
>> digits
ans = 32
>> vpa(a)
ans = (sym) 7.6137286085893726312809907207421
>> vpa(a,20)
ans = (sym) 7.6137286085893726313
>> digits(15)
>> vpa(a)
ans = (sym) 7.61372860858937
>> a1=2/3
a1 = 0.6667
>> a2=sym(2/3)
warning: passing floating-point values to sym is dangerous, see "help sym"
warning: called from
double_to_sym_heuristic at line 50 column 7
sym at line 384 column 11
a2 = (sym) 2/3
>> a3=vpa('2/3',32)
a3 = (sym) 0.66666666666666666666666666666667
>> format long
>> a1
a1 = 0.6666666666666673.2.3 符号对象与数值对象的转换
>> a=sym('2*sqrt(5)+pi')
a = (sym)
___
pi + 2*\/ 5
>> b1=double(a1)
b1 = 0.666666666666667
>> a2=vpa(a=sym('2*sqrt(5)+pi'),32)
a2 = (sym) 7.6137286085893726312809907207421
>> b3=eval(a)
b3 = 7.6137286085893733.3 符号表达式的操作和转换
3.3.1 符号表达式中自由变量的确定
>> f=sym('a*x^2+b*x+c')
f = (sym)
2
a*x + b*x + c
>> findsym(f)
ans = a,b,c,x
>> g=sym('sin(z)+cos(v)')
g = (sym) sin(z) + cos(v)
>> findsym(g,1)
ans = z
>>3.3.2 符号表达式的化简
>> f=sym('x^3-6*x^2+11*x-6')
f = (sym)
3 2
x - 6*x + 11*x - 6
>> g=sym('(x-1)*(x-2)*(x-3)')
g = (sym) (x - 3)*(x - 2)*(x - 1)
>> h=sym('x*(x*(x-6)+11)-6')
h = (sym) x*(x*(x - 6) + 11) - 6
>> pretty(f)
3 2
x - 6*x + 11*x - 6
>> collect(g)
error: Python exception: TypeError: collect() missing 1 required positional argume
nt: 'syms'
occurred at line 1 of the Python code block:
return collect(*_ins)
error: called from
pycall_sympy__ at line 179 column 7
collect at line 59 column 3
>> collect(g,'x')
ans = (sym) (x - 3)*(x - 2)*(x - 1)
>> f1=sym('x^3+2*x^2*y+4*x*y+6')
f1 = (sym)
3 2
x + 2*x *y + 4*x*y + 6
>> collect(f1,'y')
ans = (sym)
3 / 2 \
x + y*\2*x + 4*x/ + 6
>> expand(g)
ans = (sym)
3 2
x - 6*x + 11*x - 6
>> horner(f)
ans = (sym) x*(x*(x - 6) + 11) - 6
>> factor(f)
ans = (sym) (x - 3)*(x - 2)*(x - 1)
>> y=sym('cos(x)^2+sin(x)^2')
y = (sym)
2 2
sin (x) + cos (x)
>> y=sym('cos(x)^2-sin(x)^2')
y = (sym)
2 2
- sin (x) + cos (x)
>> simplify(y)
ans = (sym) cos(2*x)
>> simple(y)
error: 'simple' undefined near line 1, column 13.3.3 符号表达式的替换
>> syms a b c d x
>> eig([a b;c d])
ans = (sym 2x1 matrix)
[ _________________________]
[ / 2 2 ]
[a d \/ a - 2*a*d + 4*b*c + d ]
[- + - - ----------------------------]
[2 2 2 ]
[ ]
[ _________________________]
[ / 2 2 ]
[a d \/ a - 2*a*d + 4*b*c + d ]
[- + - + ----------------------------]
[2 2 2 ]
>> f=sym('(x+y)^2+3*(x+y)+5')
f = (sym)
2
3*x + 3*y + (x + y) + 5
>> x=5
x = 5
>> f1=subs(f)
f1 = (sym)
2
/ 2 2 \ 2 2
\- sin (x) + cos (x) + 5/ - 3*sin (x) + 3*cos (x) + 20
>> f2=subs(f,'x+y','s')
f2 = (sym)
2
s + 3*x + 3*y + 5
>> f3=subs(f,'x','z')
f3 = (sym)
2
3*y + 3*z + (y + z) + 5
>> f3=subs(f,'(x+y)','s')
f3 = (sym)
2
s + 3*x + 3*y + 5
>> f
f = (sym)
2
3*x + 3*y + (x + y) + 5
>> f3=subs(f,'x',5)
f3 = (sym)
2
3*y + (y + 5) + 20替换时有些不对。
3.3.4 求反函数和复合函数
>> f=sym('t*e^x')
f = (sym)
x
e *t
>> g=finverse(f)
error: 'finverse' undefined near line 1, column 3
The 'finverse' function belongs to the symbolic package from Octave
Forge but has not yet been implemented.3.3.5 符号表达式的转换