损失函数与分类精度的关系

1 问题

在不同情况下损失函数的变化与分类精度的关系。
卷积核方面的运算。

2 方法

了解损失函数的分类情况，进一步了解其与分类精度的关系。
损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。
损失函数是机器学习中非常重要的一个概念，它用于衡量模型预测结果与真实结果之间的差异，从而指导模型的训练。目前，常用的损失函数有以下几种类型：
1. 均方误差损失函数（Mean Squared Error,MSE）：该函数是最常见的损失函数之二，用于具归问题。它的计算方式是将预测值与真实值之差的平方求和后取平均。MSE越小，表示模型的预测结果点真实结果越接近。
2. 交叉熵损失函数（Cross-Entropy Loss,CE）：该函数常用于分类问题，它的计算方式基于信息熵理论，衡量预测结果与真实结果之间的差异度。交叉熵越小，表示模型的预测结果与真实结果越相似。
  3.対数失函数（Logarithmic Loss， LogLoss）：対数损失函数也是常用于分类问题的一种损失函数，它的计算方式是将预测值与真实值的对数差的平均值作为损失。对数损失函数越小，表示模型的预测结果越接近真实结果。
  4.Hinge 损失函数：该函数常用于支持向量机（SVM）等分类算法中，它的计算方式是对误分类的样本进行惩罚。Hinge 损失函数越小，表示模型的分类效果越好。
3. KL 散度损失函数（Kullback-Leibler Divergence, KL）：
  该函数常用于表示两个分布之间的差异度。在机器学习中，KL散度损失函数通常用于生成模型中，用于衡量生成模型生成的样本分布与真实样本分布之间的差异度。
通过学习了解卷积层的输入输出公式及其卷积核的运算

将输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核(滤波器)。

一般可以看作对某个局部的加权求和；它的原理是在观察某个物体时我们既不能观察每个像素也不能一次观察整体，而是先从局部开始认识，这就对应了卷积。卷积核的大小一般有1x1,3x3和5x5的尺寸（一般是奇数x奇数）

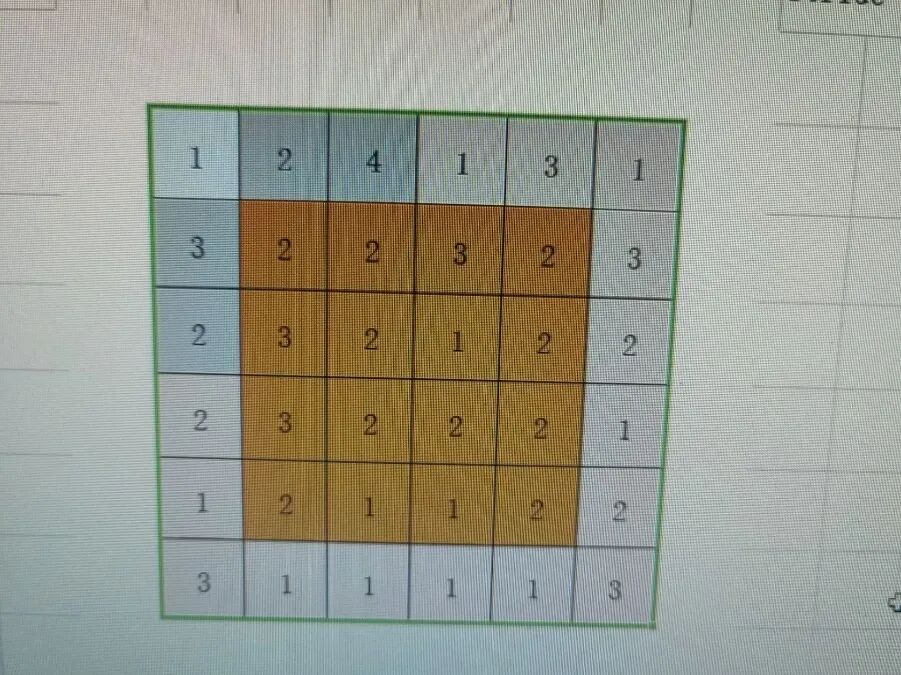
例如：卷积核为3运算后，shape为4x4：

3 结语

在这次实践的学习中，不同的损失函数对分类精度产生的效果也不相同，损失函数评价预测值和真实值，我们通过不同的损失函数得到了明显的差异效果。通过卷积层的运算，我们知道了从局部开始观察物体，然后对应着卷积，更加熟悉了卷积的原理，也对它的运用更加轻松。