【数据结构-初阶】二叉树---链式存储

🎈主页传送门****:良木生香

🔥个人专栏:《C语言》 《数据结构-初阶》 《程序设计》

🌟人为善,福随未至,祸已远行;人为恶,祸虽未至,福已远离

---

上期回顾：在上一篇文章中，我们对二叉树的顺序存储结构进行了详细的学习，知道了二叉树的顺序存储结构方式是---也就是以堆的方式进行存储，那么我们想着，既然有顺序存储结构，那有没有链式的存储结构呢？答案是，有的兄弟，有的，那么这篇文章我们就来讲讲，二叉树的链式存储结构

目录

一、二叉树的链式结构

二、二叉树的创建

2.1、创建二叉树节点

2.2、二叉树节点的链接

三、链式二叉树的基本操作

3.1、前序遍历

3.2、中序遍历

3.3、后序遍历

3.4、计算二叉树的总结点个数

3.5、计算二叉树的叶子结点个数

3.6、计算第k层节点个数

3.7、计算二叉树的深度

3.8、查找元素

3.9、层序遍历

3.10、判断是否为完全二叉树

3.11、外部代码的引入

四、综合代码

---

一、二叉树的链式结构

既然是链式结构，那么结构肯定是跟链表挂钩的，在二叉树的讲解时我们说过，二叉树的链式结构我们分为二叉链和三叉链，在这个阶段，我们主要就二叉链展开说明，我也不卖关子了，下面就是二叉链的结构体：

//链式二叉树的节点
typedef struct BinaryTree {
	Elemtype data;
	struct BinaryTree* leftChild;
	struct BinaryTree* rightChild;
}BTNode;   //将二叉树的节点重命名为BTNode

在一个二叉树的节点中，我们依旧分为数据域和指针域，数据域就是当前节点的值，指针域则包含了其左子树和右子树的指针（地址），方便直接找到左右子树

二、二叉树的创建

在我们现在这个阶段，想要实现增删查改的操作是有点难度的，这就涉及到平衡二叉树等等知识点，所以为了大家方便理解二叉树的基本性质和快速上手二叉树，我们今天就不对链式结构的二叉树进行增删查改的操作了，我们直接上手，手动创建一棵二叉树：

2.1、创建二叉树节点

二叉树节点的创建与链表节点的创建相类似，下面请看详细代码：

//先创建新节点
BTNode* BuyNode(Elemtype data) {
	//申请空间
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL) {
		perror("create new node fail!\n");
	}
	newNode->data = data;
	newNode->leftChild = newNode->rightChild = NULL;
	return newNode;
}

小贴士：在创建完节点之后，要记得将新节点返回哦，博主就是在写的时候就是忘记了返回节点地址，导致后面的代码运行不正确

2.2、二叉树节点的链接

二叉树节点的连接,我们可以直接对节点进行操作,直接将根节点与它的左右子树相连接:

BTNode* createNewBT() {
    //创建新节点
	BTNode* NodeA = BuyNode('A');
	BTNode* NodeB = BuyNode('B');
	BTNode* NodeC = BuyNode('C');
	BTNode* NodeD = BuyNode('D');
	BTNode* NodeE = BuyNode('E');
	BTNode* NodeF = BuyNode('F');
	BTNode* NodeG = BuyNode('G');
	BTNode* NodeH = BuyNode('H');
	BTNode* NodeI = BuyNode('I');
	BTNode* NodeO = BuyNode('O');

    //直接将节点进行连接
	NodeA->leftChild = NodeB;
	NodeA->rightChild = NodeC;
	NodeB->leftChild = NodeD;
	NodeB->rightChild = NodeE;
	NodeD->leftChild = NodeH;
	NodeC->leftChild = NodeF;
	NodeF->leftChild = NodeI;
	NodeH->leftChild = NodeO;
	return NodeA;
}

这里看着代码可能觉得很多,但实际上很容易理解,我把这可二叉树给大家画一下就清晰明了了:

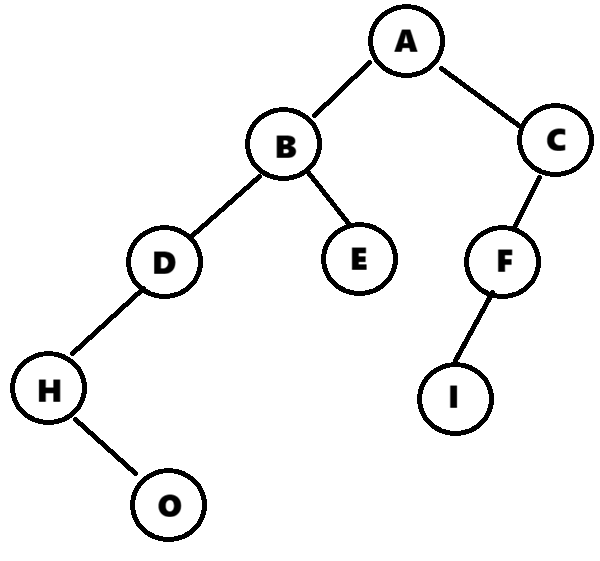
这就是今天想要讲的二叉树的例子

三、链式二叉树的基本操作

在链式二叉树中，我们对二叉树主要会进行以下操作：

• 前序遍历
• 中序遍历
• 后序遍历
• 层序遍历
• 计算二叉树的总节点个数
• 计算二叉树的叶子节点个数
• 计算二叉树第k层的节点个数
• 计算二叉树的高度/深度
• 查找二叉树中值为data的节点
• 二叉树的销毁

那么我们今天就对这些操作进行一一讲解:

3.1、前序遍历

前序遍历：就是指访问根节点的操作发生在访问左右子树之前

也就是说，现遍历根节点，再遍历左子树，最后遍历右子树

先上代码，再详细解释：

//前序遍历(根->左->右)
void PreOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	PreOrder(root->leftChild);
	PreOrder(root->rightChild);
}

在这段代码中，我们用到了递归的方法，怎么理解呢？这样看感觉得不出结果呀？不急，慢慢。首先，递归最主要的就是要有递归的终止条件，我们就从终止条件入手，就拿最后一个节点来说，请看下图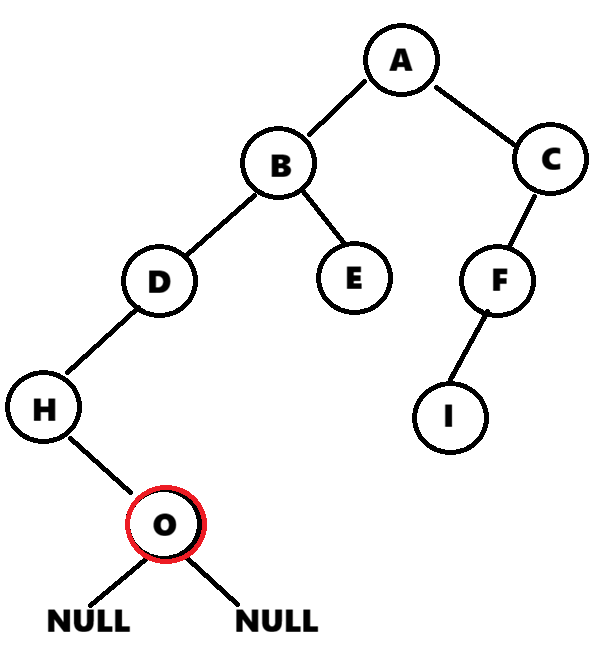：当函数中的root为节点O的时候,此时我们可以看到,O节点的左右孩子都为NULL,此时在O节点上再调用递归,PreOrder(root->leftChild)和PreOrder(root->rightChild)返回的值就是0,那么这个函数就只会打印O这个元素,那么,整个流程就是:

这段代码的运行结果为:

在遍历的过程中,严格遵循**"根->左->右"**的原则,也就是,一定先走过根节点,再把根节点的左子树遍历,再遍历左子树的左子树,直到所有左子树都遍历完了,才遍历右子树,这就是递归的基本过程.

小贴士：实在理解不了的，可以想象成，最大的根节点就是公司的董事长，下面的左右子树就是董事长的左右得力干将，再往下就又是得力干将的得力干将，也就是说，董事长现在要完成一件大事，但是自己做太麻烦，于是就把工作分给手下做，手下做完之后一级一级上报，最后就完成了这件大事，递归就是一样的道理，当最基础的员工把他的工作汇报给他的上级，他的上级又能汇报给他的上级，以此类推，最后推到根节点，完成递归

在了解了基本的递归过程之后,我们现在来看看后面的操作.

3.2、中序遍历

中序遍历：即访问根节点的操作发生在访问左子树之后，在访问右子树之前

也就是说，先把左子树全部遍历一遍，再走过根节点，左右再遍历右子树

下面是详细代码：

//中序遍历(左->根->右)
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	InOrder(root->leftChild);
	printf("%c ", root->data);
	InOrder(root->rightChild);
}

在这段代码中，递归仍然会将"左->根->右"的原则严格遵守下去,所以在我们的二叉树中,最先打印的就是整个左子树最后一个节点,O,然后会回到它的根---H,再到D,在到B,那么这段代码的运行结果为:

3.3、后序遍历

后序遍历:即访问根节点的操作发生在访问左子树和右子树之后

简而言之,就是现将左右子树全部遍历完之后,才会访问根节点

详细代码如下:

//后序遍历(左->右->根)
void LastOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	LastOrder(root->leftChild);
	LastOrder(root->rightChild);
	printf("%c ", root->data);
}

在这段代码中,也会严格遵循"左->右->根"的原则,会先彻底的将左子树全部遍历完,在将右子树彻底的全部遍历完,最后才是根节点,那么,这段代码的运行结果为:

3.4、计算二叉树的总结点个数

想要实现这个操作，我们有两种方法，一种是在遍历到一个节点的时候，用变量size++,记录下现在的数量,第二种就是通过递归的方式,统计出所有的节点个数.这两种方法看起来都可行,但是实际分析下来,第一种方式就需要借助其他的数据结构,像栈和队列,而且效率非常的低,那么我们浸提那就采用第二种方式---递归,来解决这个问题

我们的思路是,先递归左子树,再递归右子树,最后将他们两个的总数相加,具体代码如下:

//现在计算的是二叉树的节点个数
int BinaryTreeSize_of_Node(BTNode* root) {
	//整体思路是将左子树和右子树的结点个数相加
	if (root == NULL) {
		return 0;
	}
	return 1 + BinaryTreeSize_of_Node(root->leftChild) + BinaryTreeSize_of_Node(root->rightChild);
}

依旧是看成大老板想要计算出总结点个数,然后交给root->leftChild和root->rightChild两个得力干将,这两个得力干将再将任务交给他们的得力干将,最后由最后一个人计算出他的节个数,返回给他的老板,老板再返回给他的老板,以此类推,这样就统计出所有的节点个数了

3.5、计算二叉树的叶子结点个数

这个操作其实就是在3.4操作上多了一个限制条件,何为叶子结点?就是没有左右孩子的节点,那就是当leftChild==NULL和rightChild==NULL时,返回1,就证明了这是一个叶子结点,那么具体代码如下:

// 计算叶子节点个数
int BinaryTreesize_of_Leaf(BTNode* root) {
	if (root == NULL) return 0;
	if (root->leftChild == NULL && root->rightChild == NULL) return 1;
	return BinaryTreesize_of_Leaf(root->leftChild) + BinaryTreesize_of_Leaf(root->rightChild);
}

递归的方法与思想上面已经讲过,那么这里和下面的代码就不对递归进行过多赘述

3.6、计算第k层节点个数

在这个操作中,我们采用--k的方法.怎么说呢,虽然是计算第k层的节点个数,大家可不要一直想着,到这一层直接无脑把这层的节点统计出来,而是通过递归的方式,先彻底统计左子树的第k层将节点数,再彻底统计右子树的节点数,最后相加,是这样子来的,再说明晚方法之后,我们直接上代码:

// 计算第k层节点个数
int BinaryTreeSize_of_K(BTNode* root, int k) {
	if (root == NULL) return 0;
	if (k == 1) return 1;
	return BinaryTreeSize_of_K(root->leftChild, k - 1) + BinaryTreeSize_of_K(root->rightChild, k - 1);
}

当k==1的时候,不论k是因为用户输入的k=1,还是递归后k=1,都只会有一个节点而已,为什么?因为是二叉树呀,只分为左右子树,那你第k-1层的节点的左子树肯定只有一个节点嘛,所以return 1;

3.7、计算二叉树的深度

这个操作有点说法，（其实每个操作都有说法嘻嘻嘻），想要计算二叉树的深度，我们就要把左右子树的层数都计算出来，比较看看哪个层数大，大的那个就是这棵二叉树的层数了，依旧是递归，我们直到，当递归到最后一层的最后一个节点时，其左右节点都是NULL,那么这时候就能return 1,为什么?因为最后一个节点就是一层,在通过一层一层返回后,就得到了整个子树的高度:

// 计算二叉树深度
int BinaryTreeSize_of_Depth(BTNode* root) {
	if (root == NULL) return 0;
	int leftD = BinaryTreeSize_of_Depth(root->leftChild);
	int rightD = BinaryTreeSize_of_Depth(root->rightChild);
	return 1 + (leftD > rightD ? leftD : rightD);
}

3.8、查找元素

这个操作算是比较简单的，我们依旧可以通过递归的方式，遍历整个二叉树，如果存在这个元素，那就printf("找到了!"),没有的话,就printf("没找到").

// 查找元素
void BinaryTreeSearch_of_val(BTNode* root, Elemtype val) {
	if (root == NULL) return;
	if (root->data == val) {
		printf("找到了!\n");
		return;
	}
	BinaryTreeSearch_of_val(root->leftChild, val);
	BinaryTreeSearch_of_val(root->rightChild, val);
}

3.9、层序遍历

层序遍历,指的是先范文第一层节点,然后从左到右再访问第二层节点,在到第三层....以此类推,我们想要实现这个操作,就要借助一个数据结构------队列,只有队列才能更好的帮助我们实现这个功能,整体思路如下:

1.先将根节点入队,此时队列肯定不为空

2.取此时队头的元素并打印,如果左右孩子存在,再将头结点的左右孩子入队

3.循环此操作直到队列为空

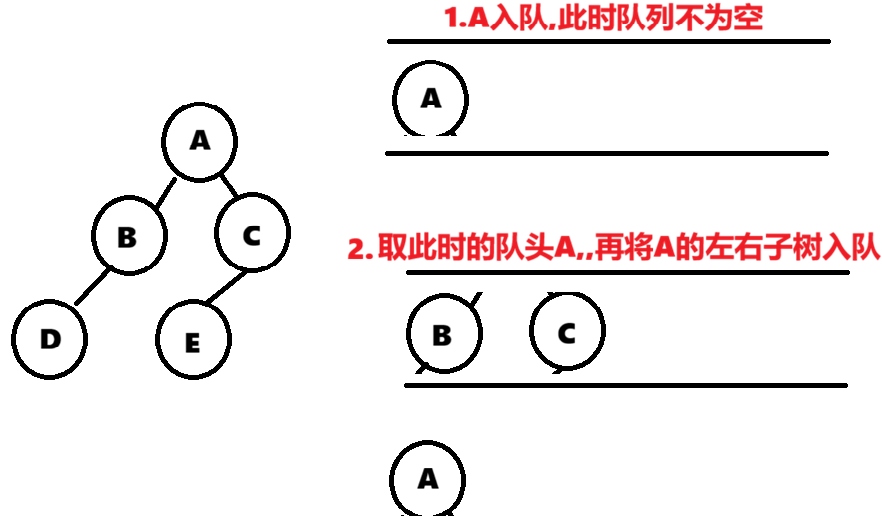
将上面这个三个步骤循环至队列为空,就可以得到:A B C D E这样的遍历结果,详细代码如下:

//现在是层序遍历
void LevelOrder(BTNode* root) {
	Queue q;
	Queue* pQueue = &q;
	InitQueue(pQueue);
	//先将根节点入队,然后循环判断队列是否为空,如果不为空,那就将根节点出队,然后将根节点的左右孩子入队,如此反复
	Push_Queue(pQueue, root);
	while (!isEmpty(pQueue)) {
		//不为空,取出队头元素,然后将队头元素删除
		BTNode* top = GEtElemFront(pQueue);
		printf("%c ", top->data);
		Pop_Queue(pQueue);
		if (top->leftChild) {
			Push_Queue(pQueue,top->leftChild);
		}
		if (top->rightChild) {
			Push_Queue(pQueue, top->rightChild);
		}
		
	}
	DetoryQueue(pQueue);
}

小贴士:在这里我们借用了队列的数据结构来实现层序遍历,那我们在编写代码的时候就可以将之前写过的队列的代码引用到我们当前的代码中,具体操作本文后面会讲到.

3.10、判断是否为完全二叉树

想要判断是否为完全二叉树，我们就要先明白，什么是完全二叉树.在之前的文章中,我们有讲到,完全二叉树就是除了最后一层,其他层的节点必须是满的,如果在非最后一层的节点又不是满的,拿着可数就不是完全二叉树,

想要判断是不是完全二叉树,我们可以通过层序遍历的方式,注意判断每一层节点(最后一层除外)是否都被填满了,当出现了空节点,那就要判断后面的所有节点是不是都为空,如果都为空,那就证明,这棵树是完全二叉树,如果后面的节点还有一个不为空,那就证明这棵树不是完全二叉树,下面是详细代码:

//现在来判断一下这棵树是不是完全二叉树
bool IsBinaryTree_of_Complete(BTNode* root) {
	Queue q;
	Queue* pQueue = &q;
	InitQueue(pQueue);
	//先将根节点入队,随后循环判断队列是否为空,不为空,将根节点出队,再把根节点的左右孩子入队
	Push_Queue(pQueue, root);
	while (!isEmpty(pQueue)) {
		QElemtype top = GEtElemFront(pQueue);
		Pop_Queue(pQueue);
		if (top == NULL) {
			break;
		}
		Push_Queue(pQueue, top->leftChild);
		Push_Queue(pQueue, top->rightChild);
	}

    //发现有节点为空,那就要判断后面的节点是否都为空
	while (!isEmpty(pQueue)) {
		BTNode* top = GEtElemFront(pQueue);
		Pop_Queue(pQueue);
        //发现有节点不为空,那就直接退出循环,证明了这棵树不是完全二叉树
		if (top != NULL) {
			DetoryQueue(pQueue);
			return false;
		}
	}
	DetoryQueue(pQueue);
	return true;
}

那么以上就是我们关于二叉树的链式结构的操作的讲解了,现在我们来讲讲怎么把队列的代码引入到当前的代码中:

3.11、外部代码的引入

在vs2022编译器上,找到资源管理器的"头文件"这个选项,新建一个头文件,并且命名为"Queue.h"(命名成什么都行,但必须是英文的,主要是方便自己看得懂),像这样:

然后将我们之前实现队列的基本操作的代码粘贴到这个头文件中:

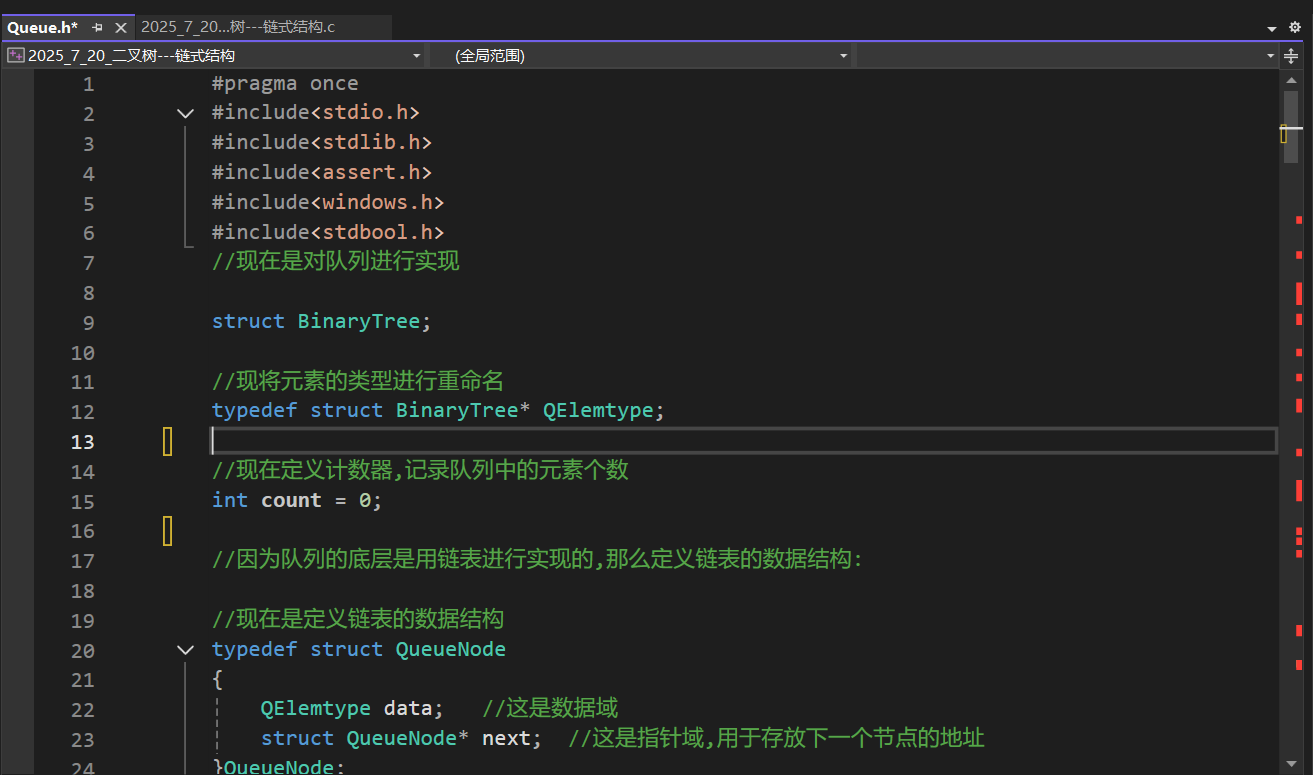
这里仅做部分展示~~~,随后在我们二叉树的代码中包含一下队列的头文件:

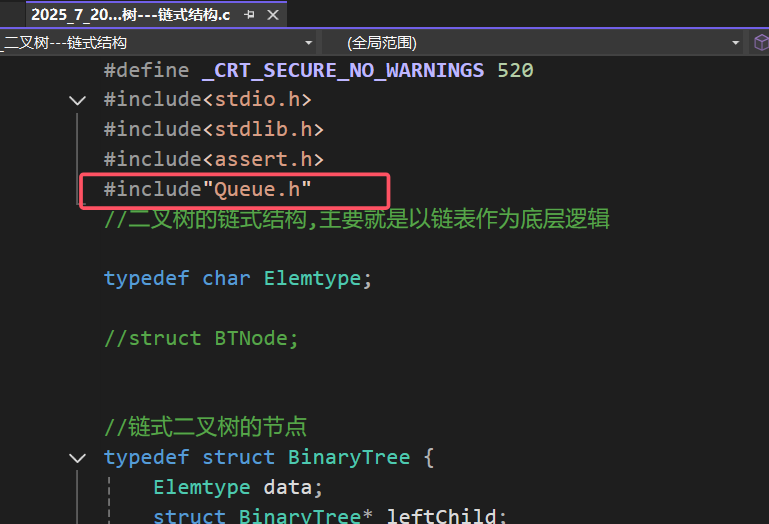
因为是我们自己引进来的,所以要将头文件用双引号引用,现在还有一个要注意的点就是,在队列的代码中,我们是将int类型重命名为了Elemtype,那么在今天的代码中,我们就要将int修改成为"struct BinaryTree*",因为我们是对二叉树的节点进行操作,那么队列的元素就是struct BinaryTree* 类型的

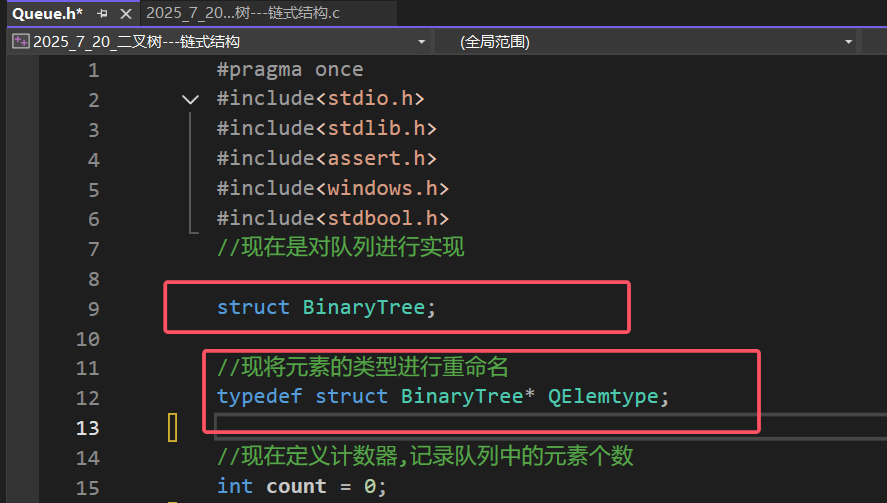
进行完这些操作之后,我们就算是把队列的代码成功引进来了

四、综合代码：

在讲解完分部的操作之后，现在我们将代码整合起来，看看效果:

现在是二叉树部分的代码:

#define _CRT_SECURE_NO_WARNINGS 520
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"Queue.h"
//二叉树的链式结构,主要就是以链表作为底层逻辑

typedef char Elemtype;

//struct BTNode;


//链式二叉树的节点
typedef struct BinaryTree {
	Elemtype data;
	struct BinaryTree* leftChild;
	struct BinaryTree* rightChild;
}BTNode;



//先创建新节点
BTNode* BuyNode(Elemtype data) {
	//申请空间
	BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
	if (newNode == NULL) {
		perror("create new node fail!\n");
	}
	newNode->data = data;
	newNode->leftChild = newNode->rightChild = NULL;
	return newNode;
}



//接下来手动创建一棵新的二叉树
BTNode* createNewBT() {
	BTNode* NodeA = BuyNode('A');
	BTNode* NodeB = BuyNode('B');
	BTNode* NodeC = BuyNode('C');
	BTNode* NodeD = BuyNode('D');
	BTNode* NodeE = BuyNode('E');
	BTNode* NodeF = BuyNode('F');
	BTNode* NodeG = BuyNode('G');
	BTNode* NodeH = BuyNode('H');
	BTNode* NodeI = BuyNode('I');
	BTNode* NodeO = BuyNode('O');

	NodeA->leftChild = NodeB;
	NodeA->rightChild = NodeC;
	NodeB->leftChild = NodeD;
	NodeB->rightChild = NodeE;
	NodeD->leftChild = NodeH;
	NodeC->leftChild = NodeF;
	NodeF->leftChild = NodeI;
	NodeH->leftChild = NodeO;
	return NodeA;
}


//对于链式结构二叉树,一共有四种遍历方式,在这里,我们先讲讲前中后三种遍历方式

//前序遍历(根->左->右)
void PreOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	PreOrder(root->leftChild);
	PreOrder(root->rightChild);
}


//中序遍历(左->根->右)
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	InOrder(root->leftChild);
	printf("%c ", root->data);
	InOrder(root->rightChild);
}


//后序遍历(左->右->根)
void LastOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	LastOrder(root->leftChild);
	LastOrder(root->rightChild);
	printf("%c ", root->data);
}



//现在计算的是二叉树的节点个数
int BinaryTreeSize_of_Node(BTNode* root) {
	//整体思路是将左子树和右子树的结点个数相加
	if (root == NULL) {
		return 0;
	}
	return 1 + BinaryTreeSize_of_Node(root->leftChild) + BinaryTreeSize_of_Node(root->rightChild);
}


//现在是计算二叉树叶子结点的个数
int BinaryTreesize_of_Leaf(BTNode* root) {
	if (root == NULL) {
		return 0;
	}
	if (root->leftChild == NULL && root->rightChild == NULL) {
		return 1;
	}
	return BinaryTreesize_of_Leaf(root->rightChild) + BinaryTreesize_of_Leaf(root->leftChild);
}



//现在计算第k层的结点个数
int BinaryTreeSize_of_K(BTNode* root, int k) {
	if (root == NULL) {
		return 0;
	}
	if (k == 1) {
		return 1;
	}
	else {
		return BinaryTreeSize_of_K(root->rightChild, k - 1) + BinaryTreeSize_of_K(root->leftChild, k - 1);
	}
}


//现在是计算二叉树的深度
int BinaryTreeSize_of_Depth(BTNode* root) {
	if (root == NULL) {
		return 0;
	}
	int leftDepth = BinaryTreeSize_of_Depth(root->leftChild);
	int rightDepth = BinaryTreeSize_of_Depth(root->rightChild);
	return 1 + (leftDepth > rightDepth ? leftDepth : rightDepth);
}



//现在是查找二叉树二元素
void BinaryTreeSearch_of_val(BTNode* root,Elemtype val) {
	if (root == NULL) {
		return;
	}
	if (root->data == val) {
		printf("找到了!\n");
		return;
	}
	BinaryTreeSearch_of_val(root->leftChild, val);
	BinaryTreeSearch_of_val(root->rightChild, val);
}



//现在是层序遍历
void LevelOrder(BTNode* root) {
	Queue q;
	Queue* pQueue = &q;
	InitQueue(pQueue);
	//先将根节点入队,然后循环判断队列是否为空,如果不为空,那就将根节点出队,然后将根节点的左右孩子入队,如此反复
	Push_Queue(pQueue, root);
	while (!isEmpty(pQueue)) {
		//不为空,取出队头元素,然后将队头元素删除
		BTNode* top = GEtElemFront(pQueue);
		printf("%c ", top->data);
		Pop_Queue(pQueue);
		if (top->leftChild) {
			Push_Queue(pQueue,top->leftChild);
		}
		if (top->rightChild) {
			Push_Queue(pQueue, top->rightChild);
		}
		
	}
	DetoryQueue(pQueue);
}




//现在来判断一下这棵树是不是完全二叉树
bool IsBinaryTree_of_Complete(BTNode* root) {
	Queue q;
	Queue* pQueue = &q;
	InitQueue(pQueue);
	//先将根节点入队,随后循环判断队列是否为空,不为空,将根节点出队,再把根节点的左右孩子入队
	Push_Queue(pQueue, root);
	while (!isEmpty(pQueue)) {
		QElemtype top = GEtElemFront(pQueue);
		Pop_Queue(pQueue);
		if (top == NULL) {
			break;
		}
		Push_Queue(pQueue, top->leftChild);
		Push_Queue(pQueue, top->rightChild);
	}
	while (!isEmpty(pQueue)) {
		BTNode* top = GEtElemFront(pQueue);
		Pop_Queue(pQueue);
		if (top != NULL) {
			DetoryQueue(pQueue);
			return false;
		}
	}
	DetoryQueue(pQueue);
	return true;
}





//这个是main函数,用来测试函数功能
int main() {
	BTNode* NodeA = createNewBT();
	printf("前序遍历:");
	PreOrder(NodeA);
	printf("\n");
	printf("\n");

	printf("中序遍历:");
	InOrder(NodeA);
	printf("\n");
	printf("\n");

	printf("后序遍历:");
	LastOrder(NodeA);
	printf("\n");
	printf("\n");

	int size_of_totalNode = BinaryTreeSize_of_Node(NodeA);
	printf("当前二叉树的总结点个数为: %d", size_of_totalNode);
	printf("\n");
	printf("\n");

	int size_of_LeafNode = BinaryTreesize_of_Leaf(NodeA);
	printf("当前二叉树的叶子结点个数为: %d", size_of_LeafNode);
	printf("\n");
	printf("\n");

	int size_of_KNode = BinaryTreeSize_of_K(NodeA,4);
	printf("当前二叉树的第4层的结点个数为: %d", size_of_KNode);
	printf("\n");
	printf("\n");

	int size_of_Depth = BinaryTreeSize_of_Depth(NodeA);
	printf("当前二叉树的层数为: %d", size_of_Depth);
	printf("\n");
	printf("\n");

	BinaryTreeSearch_of_val(NodeA, 'I');

	printf("层序遍历的结果为: ");
	LevelOrder(NodeA);
	printf("\n");
	printf("\n");

	if (IsBinaryTree_of_Complete(NodeA)) {
		printf("一棵完全二叉树");
	}
	else {
		printf("这不是完全二叉树...\n");
	}
	return 0;
}

现在是引进来的队列的代码:

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<windows.h>
#include<stdbool.h>
//现在是对队列进行实现

//现将元素的类型进行重命名
typedef struct BinaryTree* QElemtype;

//现在定义计数器,记录队列中的元素个数
int count = 0;

//因为队列的底层是用链表进行实现的,那么定义链表的数据结构:

//现在是定义链表的数据结构
typedef struct QueueNode
{
	QElemtype data;   //这是数据域
	struct QueueNode* next;  //这是指针域,用于存放下一个节点的地址
}QueueNode;



//现在定义队列的数据结构
typedef struct Queue
{
	QueueNode* phead;   //因为是先进先出,所以要用头指针和尾指针进行标记头尾
	QueueNode* ptail;
}Queue;




//现在是对队列的初始化
void InitQueue(Queue* pQueue)
{
	//对队列进行初始化.其实就是将头尾指指针进行初始化
	pQueue->phead = pQueue->ptail = NULL;

	//将头尾指针之为空
}



//现在进行入队操作
void Push_Queue(Queue* pQueue, QElemtype x)
{
	//想要进行入队操作,就要创建新节点
	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newNode == NULL)
	{
		printf("创建新节点失败!!!\n");
		perror("Fail reson:");
		printf("\n");
		exit(0);
	}

	//如果创建成功了:
	newNode->data = x;
	newNode->next = NULL;

	if (pQueue->phead == NULL)
	{
		pQueue->phead = pQueue->ptail = newNode;
	}

	else {
		//ptail   newNode
		pQueue->ptail->next = newNode;
		pQueue->ptail = pQueue->ptail->next;
	}
	count++;
}


//对队列进行判空
bool isEmpty(Queue* pQueue)
{
	assert(pQueue);
	return pQueue->phead == NULL;
}

//现在进行出队操作
void Pop_Queue(Queue* pQueue)
{
	assert(pQueue);
	//phead  phead->next
	if (pQueue->phead == NULL)
	{
		printf("队列为空,无法出队!!!\n");
		perror("Fail reason: ");
		exit(0);
	}
	//phead		phead->next		phead->next->next
	//			   next
	QueueNode* next = pQueue->phead->next;
	free(pQueue->phead);
	pQueue->phead = next;
	count--;
}


//现在取出队列的头数据
QElemtype GEtElemFront(Queue* pQueue)
{
	assert(pQueue);
	if (isEmpty(pQueue))
	{
		exit(1);
		
	}
	return pQueue->phead->data;
}




//现在取出队尾数据
QElemtype GetElemTail(Queue* pQueue)
{
	assert(pQueue);
	if (pQueue->ptail != NULL)
	{
		return pQueue->ptail->data;
	}
	if (pQueue->ptail == NULL) {
		return NULL;
	}

}


//这是对队列的销毁操作
void DetoryQueue(Queue* pQueue)
{
	assert(pQueue);
	QueueNode* pcur = pQueue->phead;
	while (pcur != NULL)
	{
		QueueNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	pQueue->phead = pQueue->ptail = NULL;
}



//现在是打印队列的函数
void my_printf(Queue* pQueue)
{
	assert(pQueue);
	QueueNode* pcur = pQueue->phead;
	if (pQueue->phead == NULL)
	{
		printf("当前队列中没有元素!!!\n");

	}
	else
	{

		while (pcur != NULL)
		{
			printf("%d ", pcur->data);
			pcur = pcur->next;
		}
	}
}

以这棵二叉树为例:

那么整体的运行结果为:

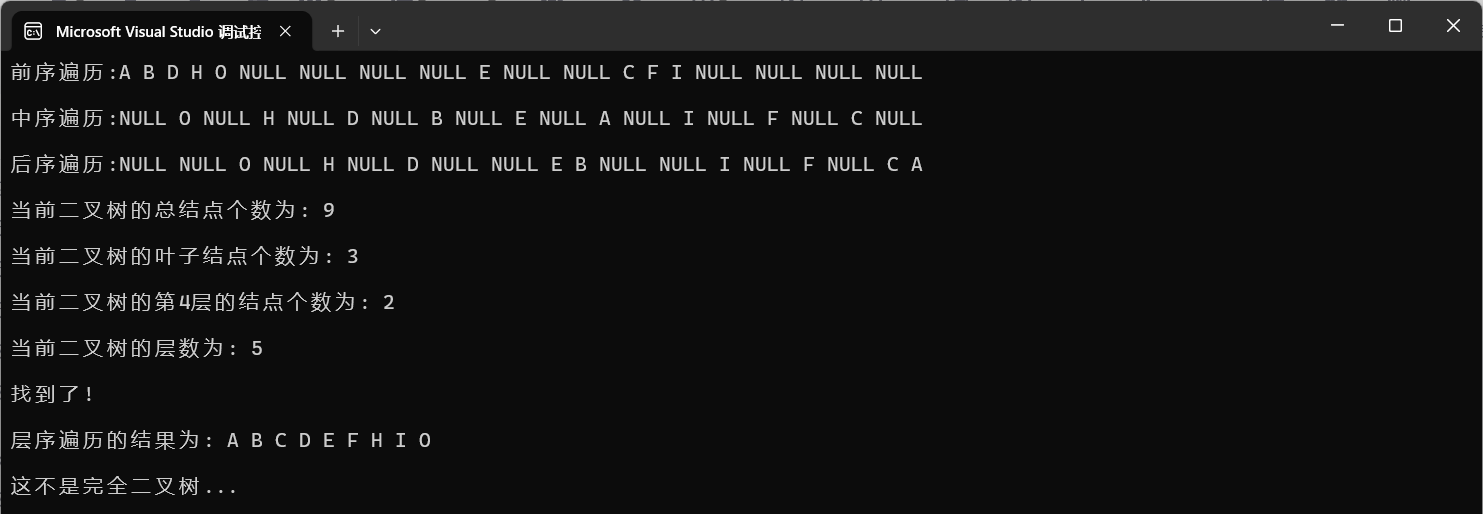
那么以上就是本次分享有关二叉树---链式存储的所有内容啦,感谢大佬们的阅读~~~

文章是自己写的哈，有什么描述不对的、不恰当的地方，恳请大佬指正，看到后会第一时间修改，感谢您的阅读.