leetcode160:相交链表

题目:

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

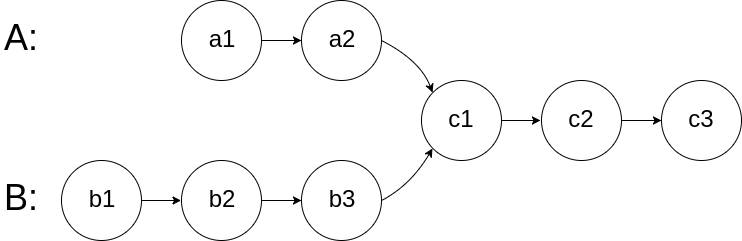
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

思路:

简单来说,就是求两个链表交点节点的指针

要注意:不是数值相等,而是指针相等

代码实现:

方法一:长度差

①先分别计算两个链表的长度,将curA指向长的链表,curB指向短的链表

②再将两个链表长度相减,得到差值

③让curA先走差值大小的长度,再同时移动两个指针

④最后返回相交的节点

cpp 复制代码

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != NULL) { // 求链表A的长度
            lenA++;
            curA = curA->next;
        }
        while (curB != NULL) { // 求链表B的长度
            lenB++;
            curB = curB->next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            swap (lenA, lenB);
            swap (curA, curB);
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap--) {
            curA = curA->next;
        }
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != NULL) {
            if (curA == curB) {
                return curA;
            }
            curA = curA->next;
            curB = curB->next;
        }
        return NULL;
    }
};

但是这种方法要遍历链表两次,一次得到长度,一次寻找节点,我们可以使用哈希表来存储遍历过的节点,如果当前节点已经在哈希表中存在,就直接返回

方法2:哈希表

①先遍历一遍其中一个链表,将里面的节点存入哈希表中

②再遍历另一个链表,判断链表中的节点是否存在哈希表中

③如果存在就说明相交,全部遍历完还没找到相交节点说明不相交

cpp 复制代码

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (!headA || !headB) return nullptr;        
        unordered_set<ListNode*> visited;
        ListNode* curr = headA;
        // 第一遍遍历链表A，将所有节点加入哈希表
        while (curr) {
            visited.insert(curr);
            curr = curr->next;
        }
        // 第二遍遍历链表B，检查节点是否已在哈希表中
        curr = headB;
        while (curr) {
            if (visited.find(curr) != visited.end()) {
                return curr;  // 找到第一个公共节点
            }
            curr = curr->next;
        }        
        return nullptr;  // 没有交点
    }
};

哈希表的方法比较清晰简单,但是需要使用到额外的空间,可以使用双指针的方式,避免额外空间的使用

方法3.双指针

①将两个指针分别指向两个链表的头节点

②当两个指针不相同时,分别移动两个指针

③当其中一个指针指向当前链表结尾时,将其移动到另一个链表的头节点,继续遍历

④若相交,两个指针一定会在相交节点相遇,若不相交,两个指针一定会同时指向最后的NULL节点

cpp 复制代码

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA==nullptr||headB==nullptr)return nullptr;
        ListNode* h1 = headA;
        ListNode* h2 = headB;
        while(h1!=h2){
            //如果遍历完当前链表,就将其移动到另一个链表的头节点
            if(h1==nullptr){
                h1 = headB;
            }else{
                h1 = h1->next;
            }
            if(h2==nullptr){
                h2 = headA;
            }else{
                h2=h2->next;
            }
        }
        return h1;
    }
};

双指针的方法没有使用到额外的空间,并且时间复杂度是O(n+m),属于是较优的解法了

这题我们从最开始的两次遍历,到使用额外空间的一次遍历,再到不使用额外空间的一次遍历,多次优化代码,说明一道题不只有一种解法,可以进行不断的优化,找到最优解