Python数学：几何运算

文章目录

• [一、 欧几里得几何运算](#一、 欧几里得几何运算)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 math 模块进行基础几何计算](#使用 math 模块进行基础几何计算)
    • [使用 NumPy 进行向量与矩阵运算](#使用 NumPy 进行向量与矩阵运算)
  • [3. 应用场景](#3. 应用场景)
  • • 游戏开发中的碰撞检测
    • 图形学中的变换
• [二、 解析几何运算](#二、 解析几何运算)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 SymPy 进行符号几何计算](#使用 SymPy 进行符号几何计算)
    • 参数方程与极坐标
  • [3. 应用场景](#3. 应用场景)
  • • 轨迹分析与路径规划
• [三、 射影几何运算](#三、 射影几何运算)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 OpenCV 进行射影变换](#使用 OpenCV 进行射影变换)
• [四、 微分几何运算](#四、 微分几何运算)
• • [1. 基本概念](#1. 基本概念)
  • [2. 使用方法](#2. 使用方法)
  • • [使用 NumPy 计算曲线曲率](#使用 NumPy 计算曲线曲率)
    • 三维曲面法向量计算
• [五、 总结](#五、 总结)
• [六、 相关文章](#六、 相关文章)

---

几何运算是使用数学方法研究空间中的点、线、面、体等几何对象的性质和关系的计算过程。它通过代数、向量和微积分等工具，解决几何图形的测量、变换、关系和空间分析等问题。本篇介绍欧几里得几何运算、解析几何运算、射影几何运算和微分几何运算。

一、 欧几里得几何运算

欧几里得几何是经典几何学的基础，主要研究点、线、面在平面和空间中的位置、距离、角度等关系。在Python中，可以使用基础数学库和向量运算库来实现常见的欧几里得几何计算。

欧几里得几何运算可以直观理解为在平面上量距离、画图形、测角度的过程。

1. 基本概念

核心概念：距离、角度、面积、体积

直观理解：

• 距离计算 = 勾股定理的扩展
• 角度计算 = 余弦定理的应用
• 面积计算 = 海伦公式

关键理解：

• 距离是"最短的直线路径"：在平面上，两点间直线最短
• 角度是"转向的幅度"：从一条线转到另一条线需要转多少
• 几何运算就是测量和计算：用数学公式把直观的图形关系量化

可视化理解 :

三角形及其性质：

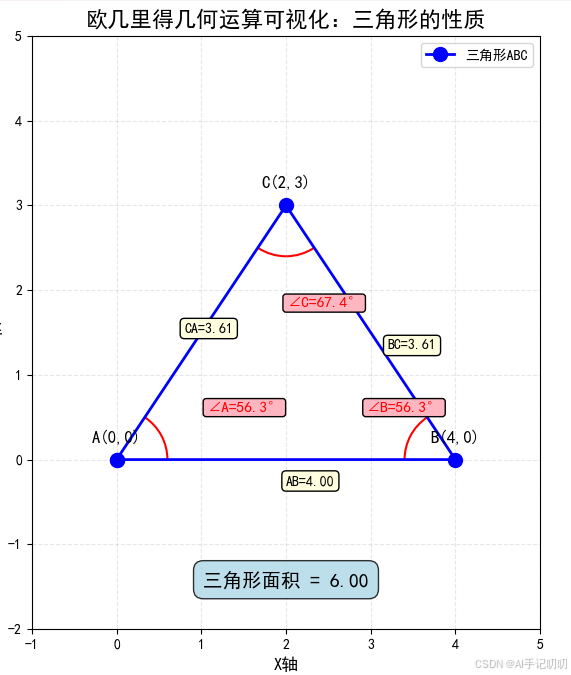
圆与距离：

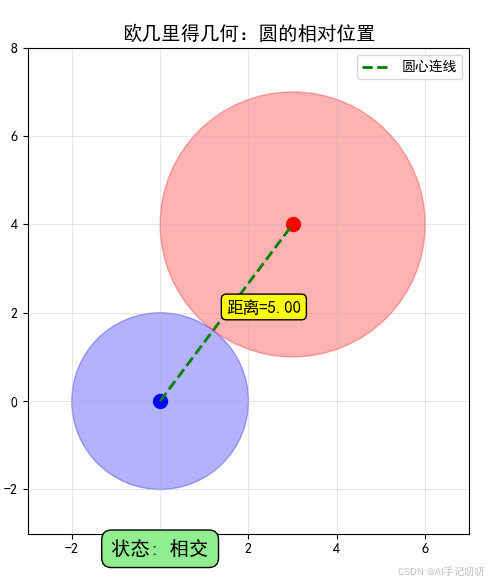
2. 使用方法

使用 math 模块进行基础几何计算

import math

def distance(x1, y1, x2, y2):
    """计算两点之间的欧氏距离"""
    return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)


def distance2(p1, p2):
    """计算两点之间的欧氏距离"""
    return math.dist(p1, p2)  # Python 3.8+    p1 和 p2 为 (x, y) 元组或列表
	
	
def angle_between(v1, v2):
    """
    计算两个二维向量之间的夹角（弧度）
    """
    dot_product = v1[0]*v2[0] + v1[1]*v2[1]
    norm1 = math.sqrt(v1[0]**2 + v1[1]**2)
    norm2 = math.sqrt(v2[0]**2 + v2[1]**2)
    return math.acos(dot_product / (norm1 * norm2))


def triangle_area(a, b, c):
    """
    使用海伦公式计算三角形面积
    a, b, c: 三角形三边长度
    """
    s = (a + b + c) / 2
    return math.sqrt(s * (s - a) * (s - b) * (s - c))
	
if __name__ == '__main__':
    print("距离:", distance(0, 0, 3, 4))
    print("夹角:", angle_between((1, 0), (0, 1)))
    print("三角形面积:", triangle_area(3, 4, 5))

使用 NumPy 进行向量与矩阵运算

import numpy as np

# 创建向量
v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])

# 基础运算
print(np.dot(v1, v2))          # 点积: 32
print(np.cross(v1, v2))        # 叉积: [-3, 6, -3]
print(np.linalg.norm(v1))      # 模长: 3.7417

# 投影计算
proj = np.dot(v1, v2) / np.dot(v2, v2) * v2

3. 应用场景

游戏开发中的碰撞检测

import math


def distance(x1, y1, x2, y2):
    return math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)


def circle_collision(c1, r1, c2, r2):
    dist = distance(c1[0], c1[1], c2[0], c2[1])
    return dist <= (r1 + r2)


def point_in_triangle(px, py, v1, v2, v3):
    def sign(p1, p2, p3):
        return (p1[0] - p3[0]) * (p2[1] - p3[1]) - (p2[0] - p3[0]) * (p1[1] - p3[1])

    d1 = sign((px, py), v1, v2)
    d2 = sign((px, py), v2, v3)
    d3 = sign((px, py), v3, v1)

    has_neg = (d1 < 0) or (d2 < 0) or (d3 < 0)
    has_pos = (d1 > 0) or (d2 > 0) or (d3 > 0)

    return not (has_neg and has_pos)


if __name__ == '__main__':
    print("圆碰撞:", circle_collision((0, 0), 5, (8, 0), 3))
    print("点在三角形内:", point_in_triangle(2, 2, (0, 0), (4, 0), (2, 4)))

图形学中的变换

import numpy as np

def transform_point(point, angle=0, scale=(1, 1), origin=(0, 0)):
    """组合变换：旋转 + 缩放"""
    angle_rad = np.radians(angle)
    rot_matrix = np.array([
        [np.cos(angle_rad), -np.sin(angle_rad)],
        [np.sin(angle_rad), np.cos(angle_rad)]
    ])
    
    scaled = np.array(scale) * (np.array(point) - np.array(origin))
    rotated = rot_matrix @ scaled
    return tuple(rotated + np.array(origin))

print(transform_point((1, 0), angle=90))  

二、 解析几何运算

解析几何将几何问题转化为代数问题，通过坐标系和方程来研究几何对象。Python中可使用符号计算库如 SymPy 进行解析几何运算。

解析几何的核心思想就是用代数方程描述几何图形

1. 基本概念

核心概念：坐标系、代数方程、参数方程

可视化理解 :

基础图形-直线、圆、抛物线：

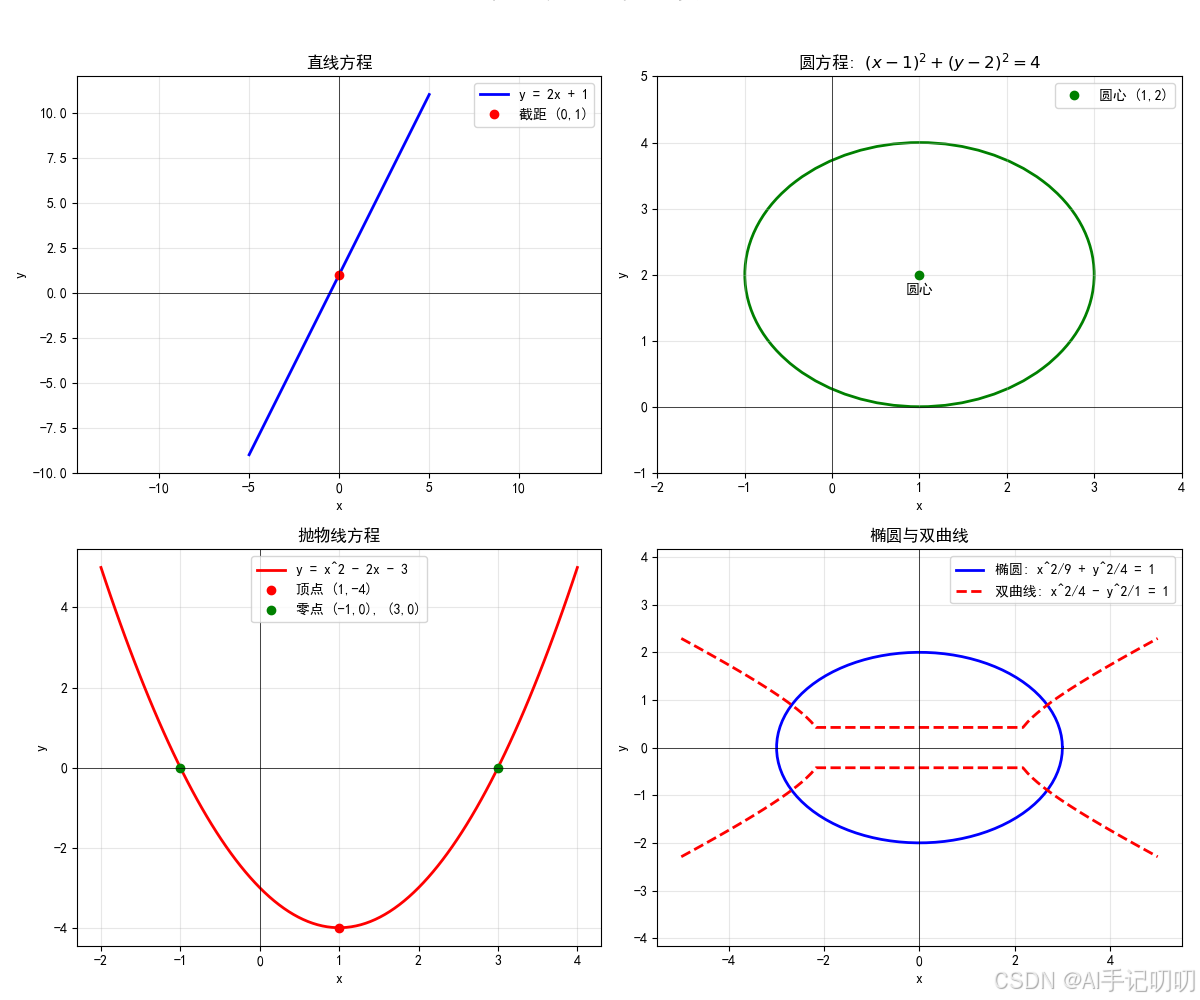
方程求解与交点可视化：

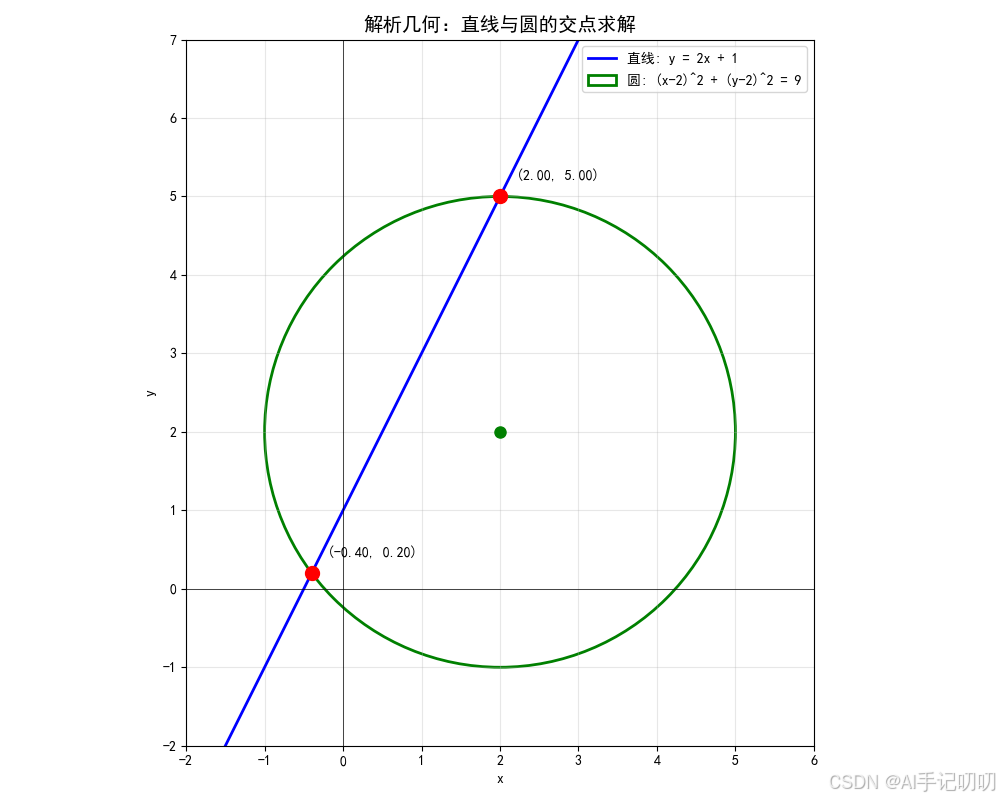
参数方程（复杂曲线）：

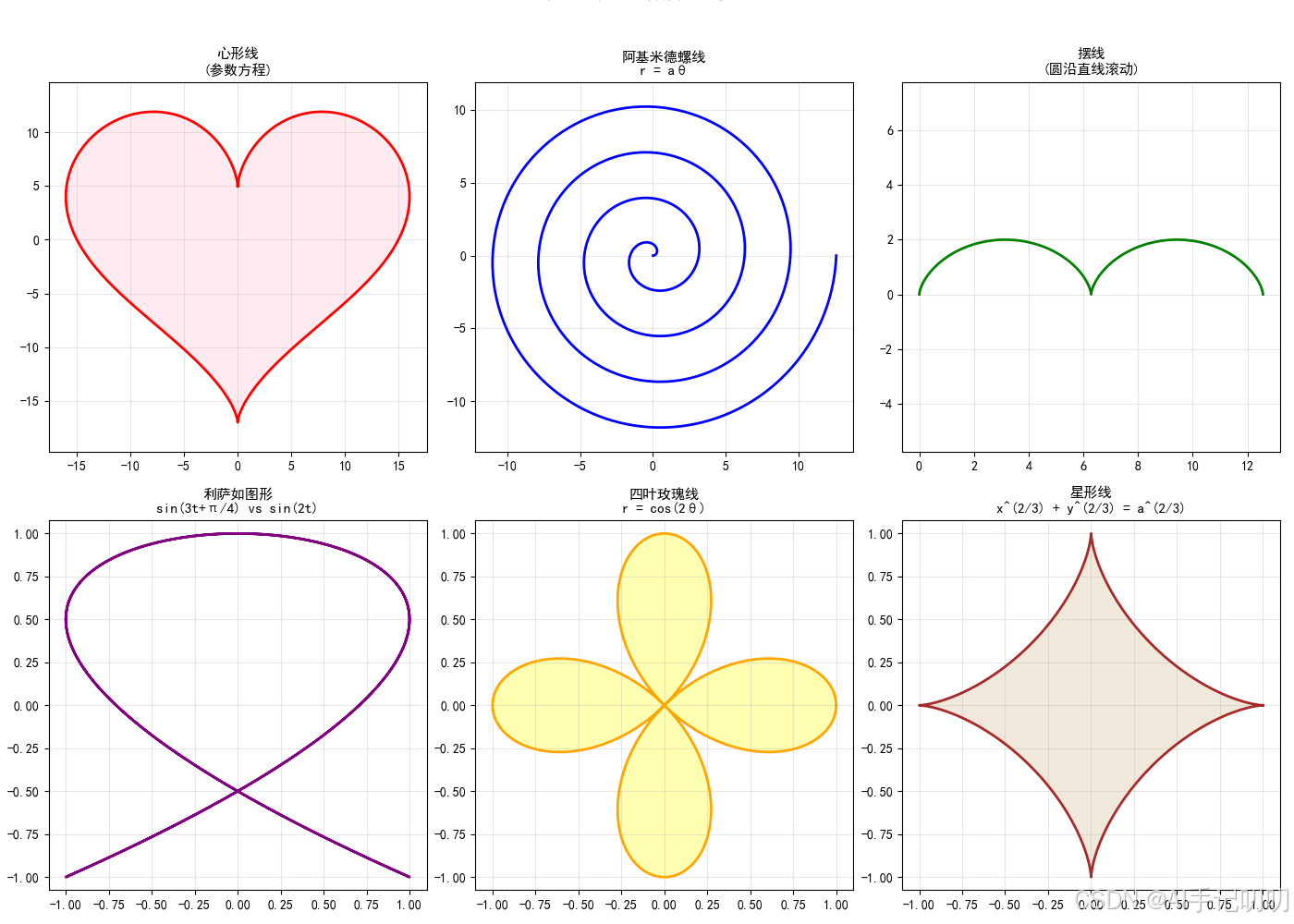
2. 使用方法

pip install sympy matplotlib

使用 SymPy 进行符号几何计算

from sympy import Point, Line, Circle, Polygon

# 创建几何对象
A, B, C = Point(0, 0), Point(4, 0), Point(2, 3)
circle = Circle(A, 5)
line = Line(A, B)

# 几何计算
print("交点:", line.intersection(circle))
print("面积:", Polygon(A, B, C).area)
print("距离:", line.distance(Point(1, 1)))

参数方程与极坐标

import numpy as np
import matplotlib.pyplot as plt
# 设置支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决'-'显示问题
plt.rcParams['axes.unicode_minus'] = False


def parametric_equations():
    """参数方程与极坐标示例"""

    # 参数方程绘制曲线
    t = np.linspace(0, 2 * np.pi, 100)
    x = np.cos(t)
    y = np.sin(t)

    plt.figure(figsize=(10, 4))

    plt.subplot(1, 2, 1)
    plt.plot(x, y)
    plt.title("参数方程: x=cos(t), y=sin(t)")
    plt.axis('equal')
    plt.grid(True)

    # 极坐标绘图
    plt.subplot(1, 2, 2, projection='polar')
    theta = np.linspace(0, 4 * np.pi, 200)
    r = np.sin(3 * theta)  # 三叶玫瑰线
    plt.polar(theta, r)
    plt.title("极坐标: r = sin(3θ)")

    plt.tight_layout()
    plt.show()


if __name__ == '__main__':
    parametric_equations()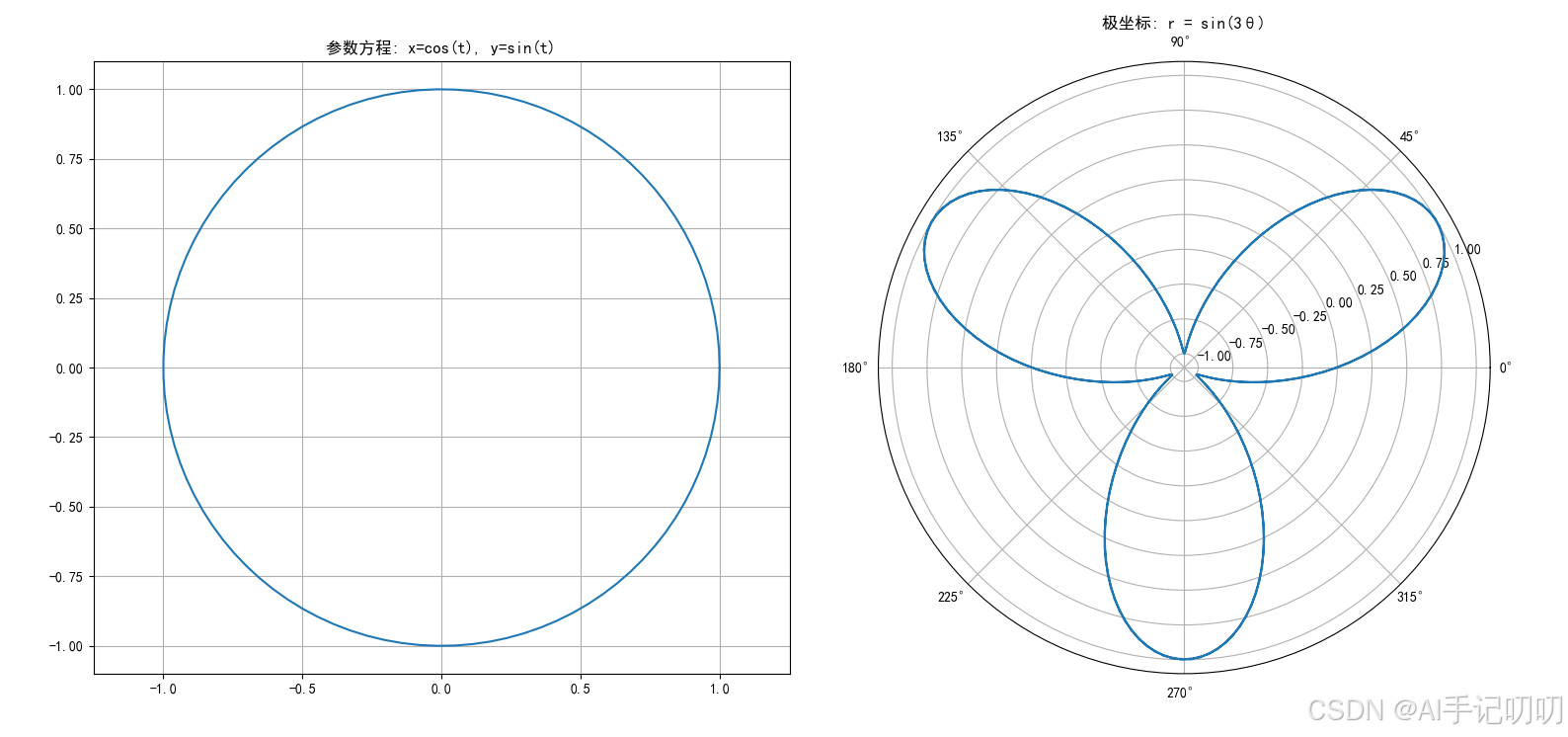

3. 应用场景

轨迹分析与路径规划

import numpy as np

def bezier_curve(control_points, n=100):
    """生成贝塞尔曲线（de Casteljau算法）"""
    t = np.linspace(0, 1, n)
    curve = np.zeros((n, 2))
    
    for i, ti in enumerate(t):
        points = control_points.copy()
        for r in range(1, len(points)):
            points = (1-ti)*points[:-1] + ti*points[1:]
        curve[i] = points[0]
    
    return curve

# 使用示例
points = np.array([[0,0], [1,3], [4,4], [6,1], [8,3]])
curve = bezier_curve(points)

三、 射影几何运算

射影几何研究在投影变换下保持不变的几何性质，常用于计算机视觉、三维重建和图像处理中。

射影几何的核心是投影变换下的不变性

1. 基本概念

核心概念：投影变换、齐次坐标、交比不变性，如交比不变性

可视化理解 :

透视投影：

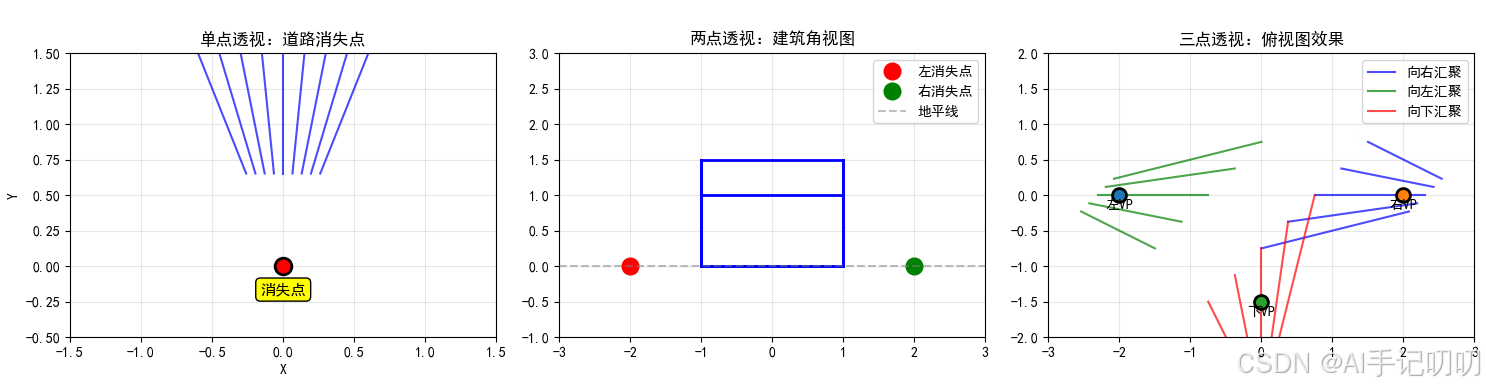
齐次坐标：

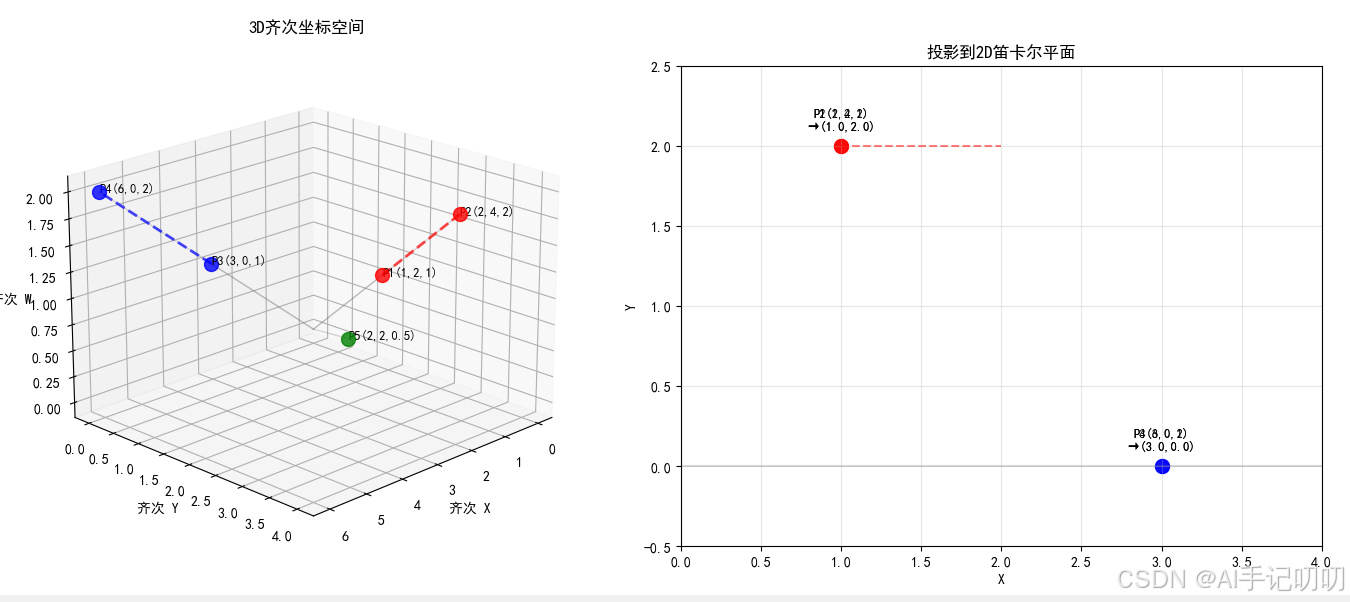
对偶原理：

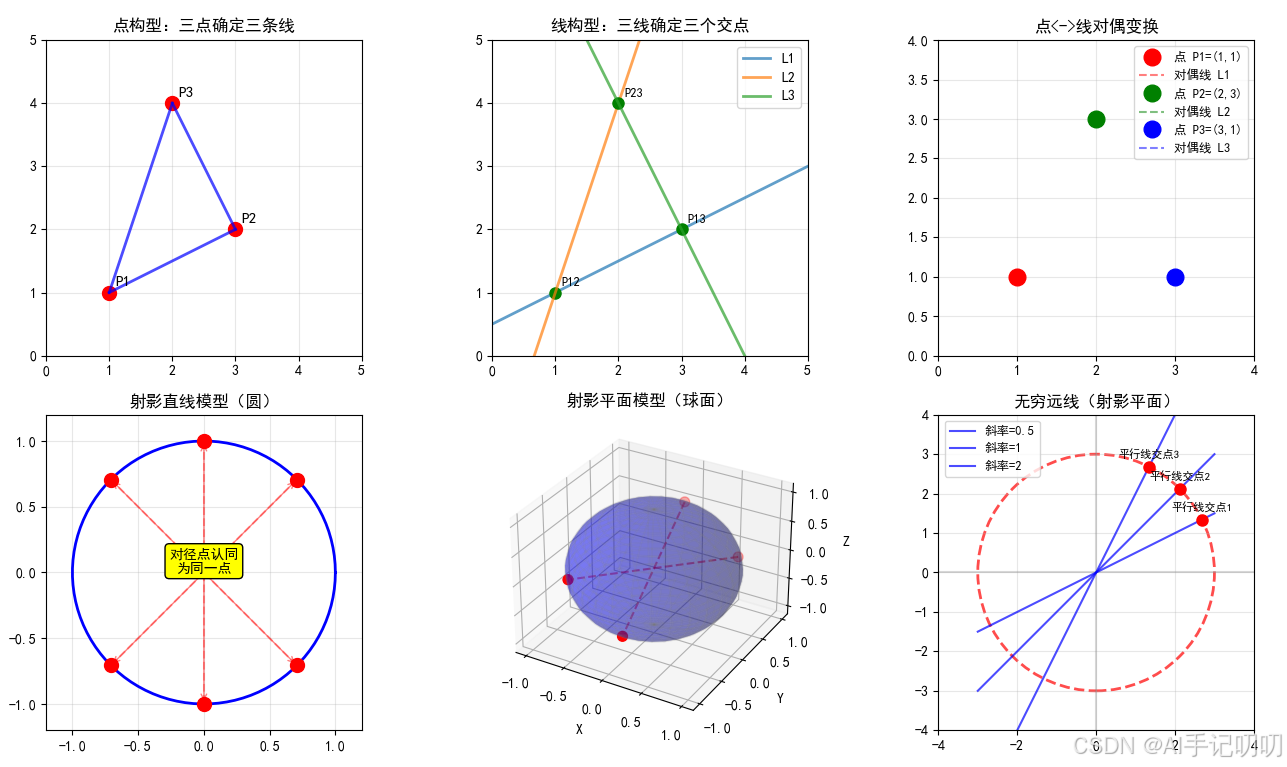
射影变换：

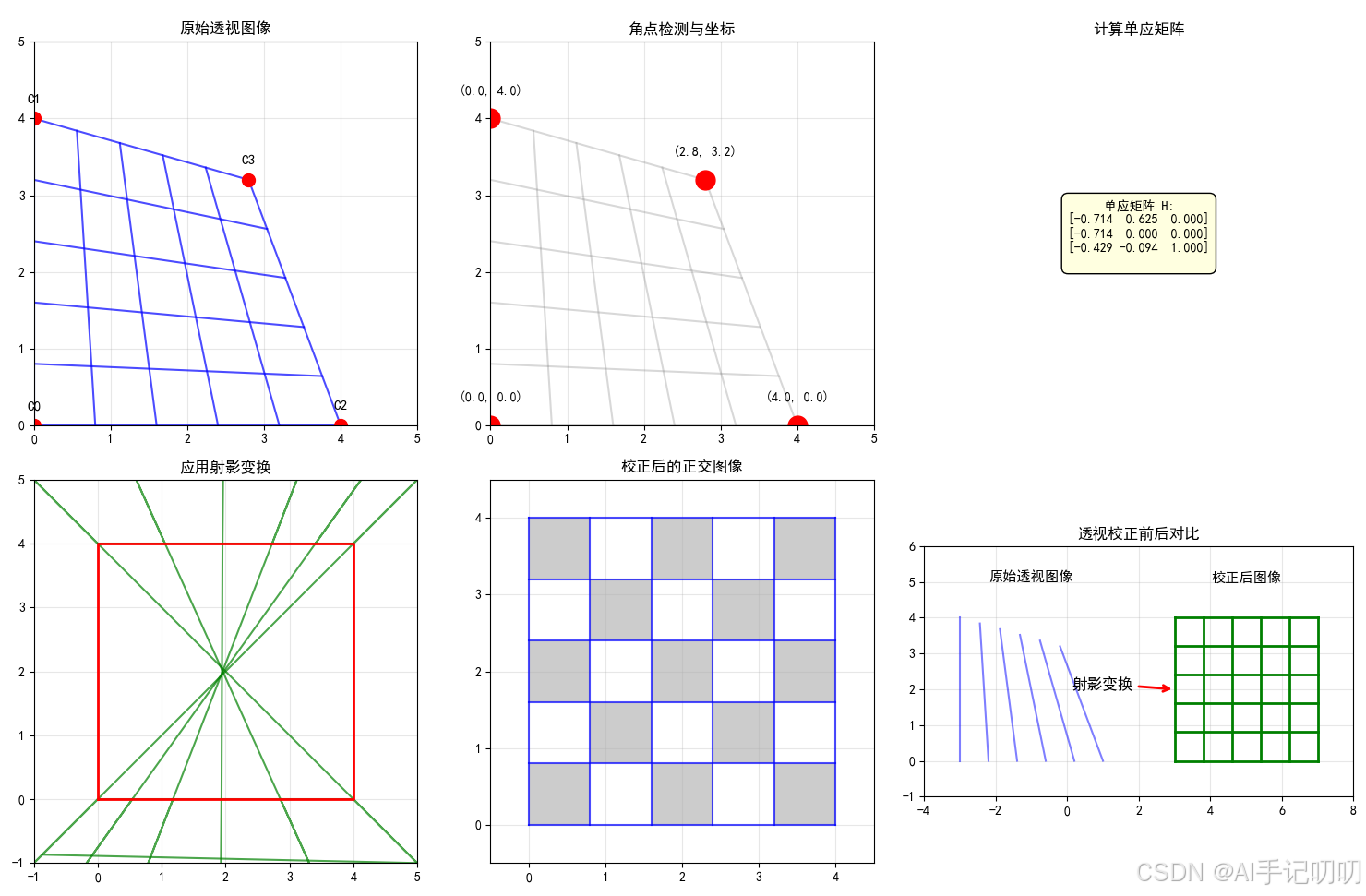
2. 使用方法

pip install opencv-python

使用 OpenCV 进行射影变换

import cv2
import numpy as np

def correct_perspective(image, src_corners, target_width, target_height):
    dst_corners = np.float32([
        [0, 0],
        [target_width, 0],
        [target_width, target_height],
        [0, target_height]
    ])
    M = cv2.getPerspectiveTransform(src_corners, dst_corners)
    corrected = cv2.warpPerspective(image, M, (target_width, target_height))
    return corrected

if __name__ == '__main__':
    # 假设有一张图片
    image = np.zeros((300, 300, 3), dtype=np.uint8)
    src_corners = np.float32([[50, 50], [250, 50], [200, 250], [80, 200]])
    corrected = correct_perspective(image, src_corners, 200, 200)
    print("校正后的图片形状:", corrected.shape)

四、 微分几何运算

微分几何研究曲线、曲面在微小范围内的性质，如曲率、法向量、切平面等，广泛应用于物理模拟、机器人学和计算机图形学。

微分几何是关于曲线和曲面的局部性质，如曲率、法向量、切平面等。

1. 基本概念

核心概念：曲率、法向量、切平面、测地线

可视化理解 :

平面曲线-曲率与密切圆：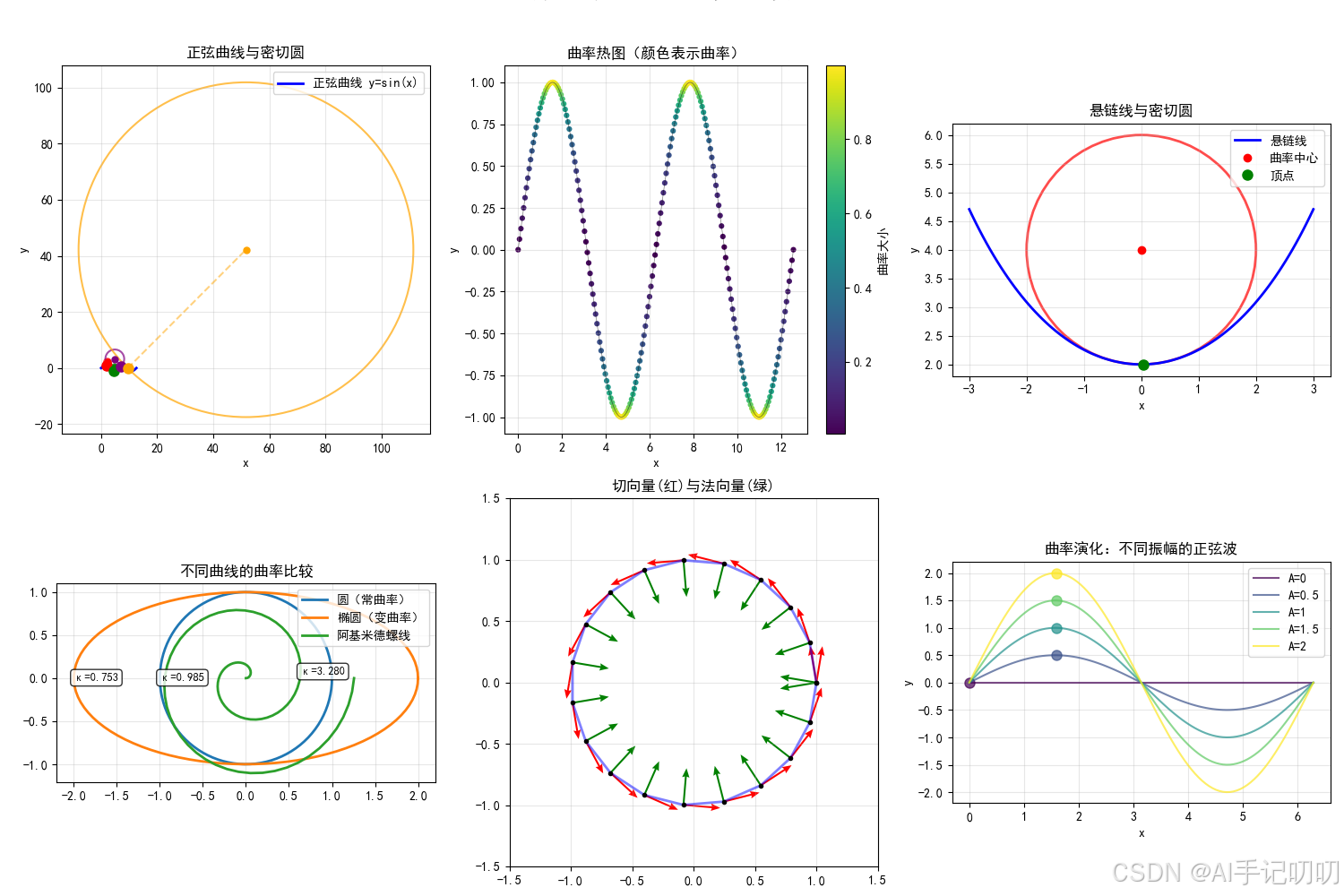

三维曲面:

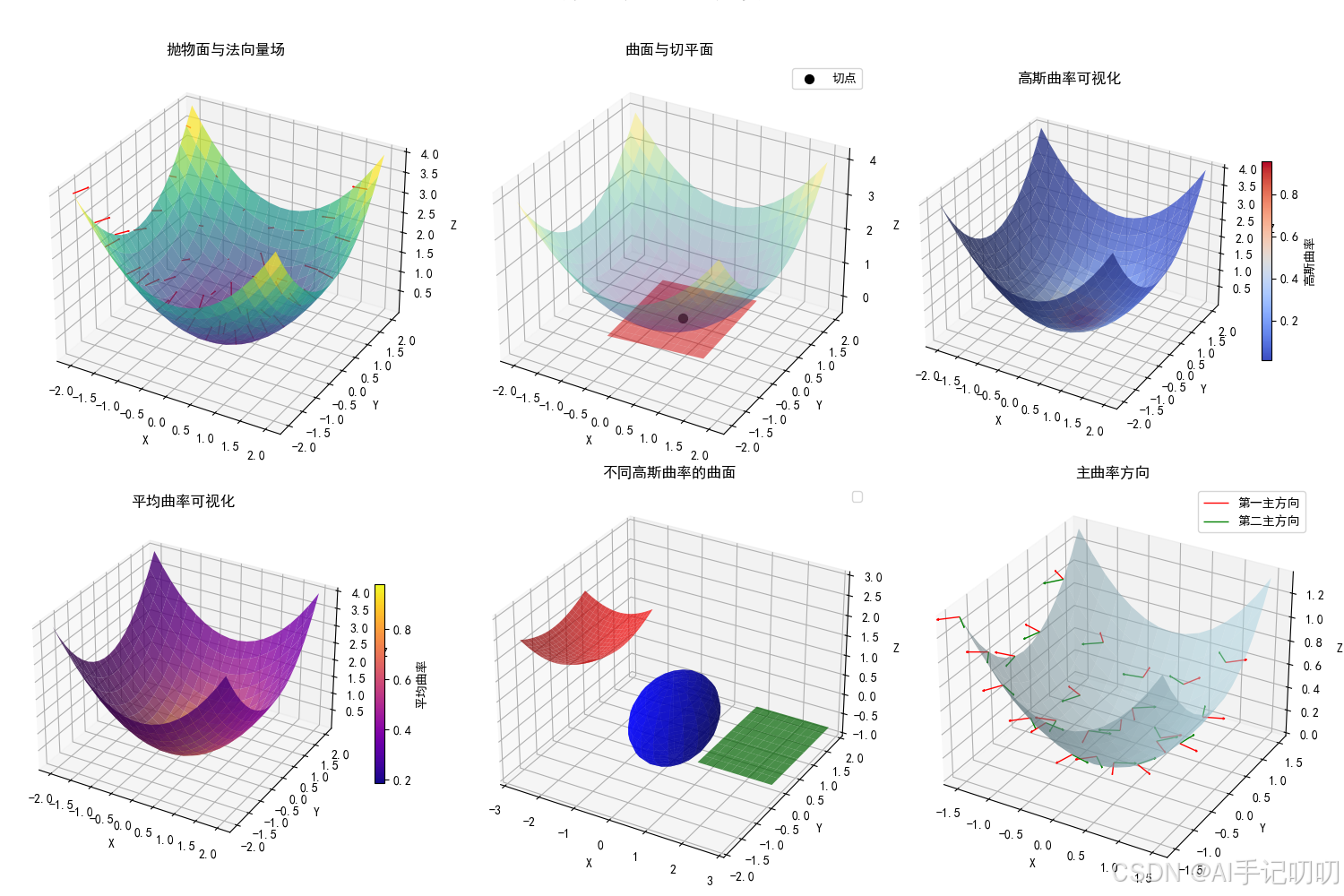
2. 使用方法

使用 NumPy 计算曲线曲率

import numpy as np

def curve_curvature(x, y):
    dx = np.gradient(x)
    dy = np.gradient(y)
    ddx = np.gradient(dx)
    ddy = np.gradient(dy)
    return np.abs(dx * ddy - dy * ddx) / (dx**2 + dy**2)**1.5

if __name__ == '__main__':
    t = np.linspace(0, 2*np.pi, 100)
    x = t
    y = np.sin(t)
    k = curve_curvature(x, y)
    print("曲率前5个值:", k[:5])

三维曲面法向量计算

import numpy as np


def compute_normals(vertices, faces):
    """计算三角网格法向量"""
    normals = np.zeros_like(vertices)

    for face in faces:
        v0, v1, v2 = vertices[face]
        normal = np.cross(v1 - v0, v2 - v0)
        normals[face] += normal

    # 归一化
    norms = np.linalg.norm(normals, axis=1, keepdims=True)
    return normals / norms

五、 总结

几何类型	主要方法	适用场景
欧几里得几何	math.dist(), math.hypot(), np.dot()	距离、角度、面积计算
解析几何	SymPy (Point, Line, Circle)	符号计算、方程求解
射影几何	cv2.getPerspectiveTransform()	图像校正、三维重建
微分几何	np.gradient(), np.cross()	曲率、法向量计算

简单计算用 math/NumPy，符号计算用 SymPy，图像处理用 OpenCV，数值计算用 SciPy。

六、 相关文章

Python数学：幂运算与根式运算
Python数学：函数运算
Python数学：统计运算

---

鼓起勇气求关注......（悄悄点一下就好，谢谢你💐）