
⚡ CYBER_PROFILE ⚡
/// SYSTEM READY ///
WARNING \]: DETECTING HIGH ENERGY
**🌊 🌉 🌊 心手合一 · 水到渠成**

|------------------------------------------------------------------------------------|--------------------------------------------------------------------------------------------------------------|
| **\>\>\> ACCESS TERMINAL \<\<\<** ||
| [**\[ 🦾 作者主页 \]**](https://blog.csdn.net/fengtinghuqu520?spm=1000.2115.3001.5343) | [**\[ 🔥 C语言核心 \]**](https://blog.csdn.net/fengtinghuqu520/category_12955956.html) |
| [**\[ 💾 编程百度 \]**](https://blog.csdn.net/fengtinghuqu520/category_13083835.html) | [**\[ 📡 代码仓库 \]**](https://blog.csdn.net/fengtinghuqu520/article/details/147275999?spm=1001.2014.3001.5502) |
---------------------------------------
Running Process: 100% \| Latency: 0ms
*** ** * ** ***
❗❗❗❗❗❗需要注意的是这里的堆和操作系统(虚拟进程地址空间)中的堆是两回事,一个是**数据结构** ,一个是**操作系统中管理内存的一块区域分段**
#### 索引与导读
* [堆的概念及结构](#堆的概念及结构)
* [🤔堆的代码实现](#🤔堆的代码实现)
*
* [Heap.h](#Heap.h)
* [Heap.c](#Heap.c)
*
* [🔭--- 比较策略实现 ---](#🔭--- 比较策略实现 ---)
* [🔭--- 核心算法 ---](#🔭--- 核心算法 ---)
*
* [堆向下调整算法](#堆向下调整算法)
* [堆的向上调整算法](#堆的向上调整算法)
* [🔭--- 接口实现 ---](#🔭--- 接口实现 ---)
*
* [堆的初始化](#堆的初始化)
* [堆的销毁](#堆的销毁)
* [堆的交换](#堆的交换)
* [堆的创建](#堆的创建)
*
* [建堆时间复杂度](#建堆时间复杂度)
* [堆的插入](#堆的插入)
* [堆的删除](#堆的删除)
* [取堆顶的数据](#取堆顶的数据)
* [堆的数据个数](#堆的数据个数)
* [堆的判空](#堆的判空)
* [堆的遍历打印](#堆的遍历打印)
* [test.c](#test.c)
* [堆的应用](#堆的应用)
*
*
*
* [堆排序](#堆排序)
* [TOP-K问题](#TOP-K问题)
* [堆(Heap)精选题解析:判定、建堆与删除](#堆(Heap)精选题解析:判定、建堆与删除)
*
* [题目一:堆的判定](#题目一:堆的判定)
*
* [💡 详细解析](#💡 详细解析)
* [题目二:堆删除操作的比较次数](#题目二:堆删除操作的比较次数)
*
* [💡 详细解析](#💡 详细解析)
* [题目三:堆排序的初始建堆](#题目三:堆排序的初始建堆)
*
* [💡 详细解析](#💡 详细解析)
* [题目四:最小堆的删除结果](#题目四:最小堆的删除结果)
*
* [💡 详细解析](#💡 详细解析)
* [💻结尾--- 核心连接协议](#💻结尾— 核心连接协议)
## 堆的概念及结构
* **概念**
堆在逻辑上是一棵**完全二叉树**,在物理存储上通常使用**数组** 来实现。
堆必须满足以下两个条件:
1. **结构性**:必须是完全二叉树。
2. **有序性** :
* **大根堆(Max Heap)** :树中任意节点的值都**大于或等于**其左右孩子节点的值。堆顶元素是最大值。
* **小根堆(Min Heap)** :树中任意节点的值都**小于或等于**其左右孩子节点的值。堆顶元素是最小值
3. **堆中某个结点的值总是不大于或不小于其父结点的值**
* 🚩**结构**
```c
typedef int HPDataType;
typedef struct Heap {
HPDataType* arr; // 底层的数组
int size; // 有效数据个数
int capacity; // 空间大小
CompareFunc cmp; // 核心:存储比较逻辑的函数指针
} HP;
```
* **`HPDataType* arr;` 底层的数组**
* **`int size;` 有效数据个数**
* **`int capacity;` 空间大小**
* **`CompareFunc cmp;` 核心:存储比较逻辑的函数指针**
堆的本质就是一个**动态数组** ,把**数组以堆的形式**呈现出来而已
*** ** * ** ***
## 🤔堆的代码实现
### Heap.h
> 这里会涉及一个关于**函数指针重命名** 的操作👇
>
> 🔗[Lucy的空间骇客裂缝:typedef用法](https://blog.csdn.net/fengtinghuqu520/article/details/150998243)
```c
#pragma once
#include
#include
#include
#include
#include
// 定义数据类型
typedef int HPDataType;
// 定义比较函数的函数指针类型
// 返回 true 表示 p1 优于 p2(需要交换或排在前面)
typedef bool (*CompareFunc)(HPDataType p1, HPDataType p2);
// 定义堆结构
typedef struct Heap {
HPDataType* arr; // 底层的数组
int size; // 有效数据个数
int capacity; // 空间大小
CompareFunc cmp; // 核心:存储比较逻辑的函数指针
} HP;
// 具体的比较策略函数(用户可调用)
bool HP_Less(HPDataType p1, HPDataType p2); // 小于 (用于小根堆)
bool HP_Greater(HPDataType p1, HPDataType p2); // 大于 (用于大根堆)
// 堆的初始化(需要传入比较策略)
void HPInit(HP* php, CompareFunc cmp);
// 堆的销毁
void HPDesTroy(HP* php);
// 堆的数据插入
void HPPush(HP* php, HPDataType x);
// 出堆(删除堆顶)
void HPPop(HP* php);
// 获取堆顶数据
HPDataType HPTop(HP* php);
// 判空
bool HPEmpty(HP* php);
// 获取大小
int HPSize(HP* php);
// 堆的打印
void HPPrint(HP* php);
```
*** ** * ** ***
### Heap.c
#### 🔭--- 比较策略实现 ---
* 🚩**如何灵活转化`小根堆`和`大根堆`???**
注意`AdjustUp` 和 `AdjustDown`中是如何使用 `php->cmp` 替代硬编码的 `<` 或 `>` 的
* 小于比较(用于构建**小根堆** :`子节点 < 父节点` 时上浮)
```c
bool HP_Less(HPDataType p1, HPDataType p2) {
return p1 < p2;
}
```
* 大于比较(用于构建**大根堆** :`子节点 > 父节点` 时上浮)
```c
bool HP_Greater(HPDataType p1, HPDataType p2) {
return p1 > p2;
}
```
*** ** * ** ***
#### 🔭--- 核心算法 ---
> 涉及**完全二叉树的性质** 👇
>
> 🔗[Lucy的空间骇客裂缝:二叉树](https://blog.csdn.net/fengtinghuqu520/article/details/156202286?spm=1011.2415.3001.5331)
##### 堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根结点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整
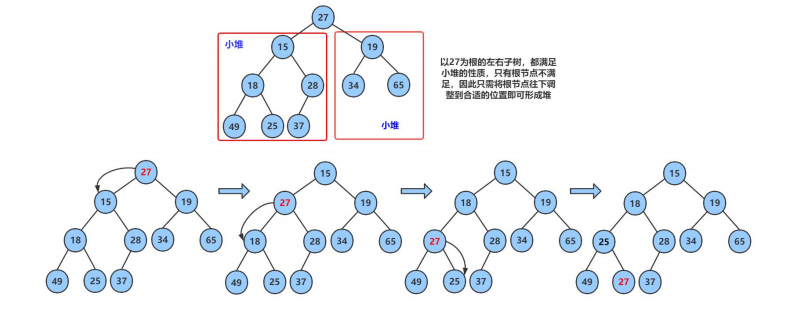
* **代码实现**
```c
// 向下调整
void AdjustDown(HP* php, int parent, int n) {
int child = parent * 2 + 1;
while (child < n) {
// 1. 选出左右孩子中"更优"的那个
// 如果右孩子存在,且右孩子比左孩子"更符合堆性质"
if (child + 1 < n && php->cmp(php->arr[child + 1], php->arr[child])) {
child++;
}
// 2. 孩子与父亲比较
// 如果孩子比父亲"更优",则交换
if (php->cmp(php->arr[child], php->arr[parent])) {
Swap(&php->arr[child], &php->arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
```
*** ** * ** ***
##### 堆的向上调整算法
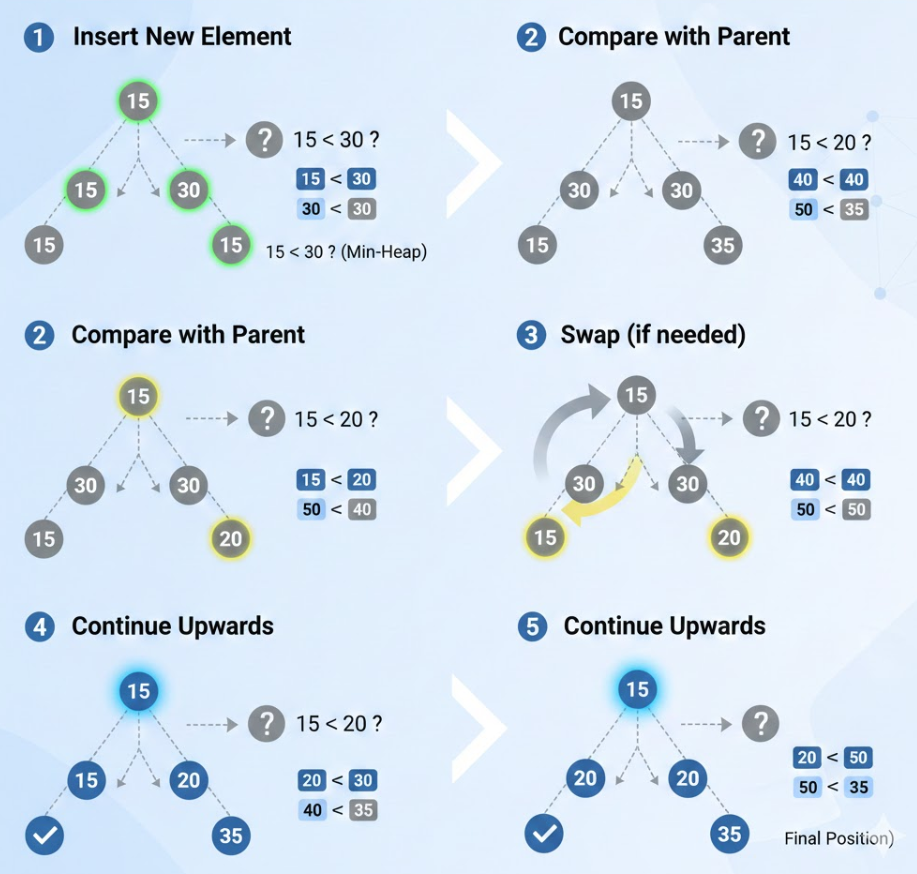
```c
void AdjustUp(HPDataType* arr, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
// 小根堆:如果孩子比父亲小,则交换
if (arr[child] < arr[parent]) {
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
```
*** ** * ** ***
#### 🔭--- 接口实现 ---
##### 堆的初始化
```c
void HPInit(HP* php) {
assert(php);
php->arr = NULL;
php->size = php->capacity = 0;
}
```
**🔥🔥🔥🔥注意:** 这里设计一个`浅拷贝`和`深拷贝`的问题
> * **浅拷贝**
> * 直接复制内存内容(如使用`memcpy()`或`简单赋值`)
> * 对于指针成员,只复制指针本身,不复制指针指向的数据
> * 新旧对象的指针指向同一块内存
> * **深拷贝**
> * 复制指针指向的实际数据
> * 为指针成员分配新的内存并复制内容
> * 新旧对象完全独立
🚩**上面的初始化函数传参就是浅拷贝**
*** ** * ** ***
##### 堆的销毁
```c
void HPDesTroy(HP* php) {
assert(php);
free(php->arr);
php->arr = NULL;
php->size = php->capacity = 0;
}
```
*** ** * ** ***
##### 堆的交换
```c
void Swap(HPDataType* x, HPDataType* y) {
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
```
🚩额外写一个`Swap`交换函数方便使用
*** ** * ** ***
##### 堆的创建
采用**向下调整算法**从给定数组构建堆
```c
void HPCreate(HP* php, HPDataType* a, int n, CompareFunc cmp) {
assert(php && a);
php->arr = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->arr == NULL) {
perror("malloc fail");
return;
}
memcpy(php->arr, a, sizeof(HPDataType) * n);
php->size = php->capacity = n;
php->cmp = cmp;
// 向下调整建堆(从最后一个非叶子节点开始)
// 时间复杂度:O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
AdjustDown(php, i);
}
}
```
**参数**
* `HP* php`: **堆结构体指针**,用于接收创建的堆
* `HPDataType* a`: **源数组**,包含初始数据
* `int n`: **数组元素个数**
* `CompareFunc cmp`: **比较函数指针**,用于定义堆的类型(最大堆/最小堆)
*** ** * ** ***
**拷贝数据**
* `memcpy(php->arr, arr, sizeof(HPDataType) * n);`
将源数组`arr`的所有数据复制到堆的内部数组中
*** ** * ** ***
向下调整建堆
* `(n - 1 - 1) / 2` 的计算:**(最后一个元素的下标 - 1) / 2**
**最后一个非叶子节点的下标**
*** ** * ** ***
###### 建堆时间复杂度
因为堆是完全二叉树,而**满二叉树也是完全二叉树**,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个结点不影响最终结果):
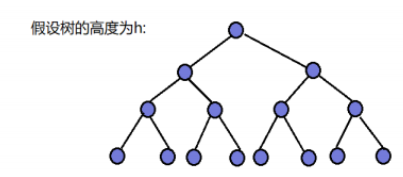
* 第1层, 2 0 2\^0 20 个节点,需要向下移动 h − 1 h-1 h−1 层
* 第2层, 2 1 2\^1 21 个节点,需要向下移动 h − 2 h-2 h−2 层
* 第3层, 2 2 2\^2 22 个节点,需要向下移动 h − 3 h-3 h−3 层
* 第4层, 2 3 2\^3 23 个节点,需要向下移动 h − 4 h-4 h−4 层
* ...
* 第h-1层, 2 h − 2 2\^{h-2} 2h−2 个节点,需要向下移动 1 1 1 层
则需要移动节点总的移动步数为:
T ( n ) = 2 0 ∗ ( h − 1 ) + 2 1 ∗ ( h − 2 ) + 2 2 ∗ ( h − 3 ) + 2 3 ∗ ( h − 4 ) + ⋯ + 2 h − 3 ∗ 2 + 2 h − 2 ∗ 1 ------ ① T(n) = 2\^0 \* (h-1) + 2\^1 \* (h-2) + 2\^2 \* (h-3) + 2\^3 \* (h-4) + \\dots + 2\^{h-3} \* 2 + 2\^{h-2} \* 1 \\quad \\text{------ ①} T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+⋯+2h−3∗2+2h−2∗1------ ①利用错位相减法:将等式 ① 左右两边同时乘以 2: 2 ∗ T ( n ) = 2 1 ∗ ( h − 1 ) + 2 2 ∗ ( h − 2 ) + 2 3 ∗ ( h − 3 ) + 2 4 ∗ ( h − 4 ) + ⋯ + 2 h − 2 ∗ 2 + 2 h − 1 ∗ 1 ------ ② 2 \* T(n) = 2\^1 \* (h-1) + 2\^2 \* (h-2) + 2\^3 \* (h-3) + 2\^4 \* (h-4) + \\dots + 2\^{h-2} \* 2 + 2\^{h-1} \* 1 \\quad \\text{------ ②} 2∗T(n)=21∗(h−1)+22∗(h−2)+23∗(h−3)+24∗(h−4)+⋯+2h−2∗2+2h−1∗1------ ②用 ② - ① 进行错位相减: T ( n ) = 1 − h + 2 1 + 2 2 + 2 3 + 2 4 + ⋯ + 2 h − 2 + 2 h − 1 T(n) = 1 - h + 2\^1 + 2\^2 + 2\^3 + 2\^4 + \\dots + 2\^{h-2} + 2\^{h-1} T(n)=1−h+21+22+23+24+⋯+2h−2+2h−1 T ( n ) = 2 0 + 2 1 + 2 2 + 2 3 + 2 4 + ⋯ + 2 h − 2 + 2 h − 1 − h T(n) = 2\^0 + 2\^1 + 2\^2 + 2\^3 + 2\^4 + \\dots + 2\^{h-2} + 2\^{h-1} - h T(n)=20+21+22+23+24+⋯+2h−2+2h−1−h T ( n ) = 2 h − 1 − h T(n) = 2\^h - 1 - h T(n)=2h−1−h已知节点总数 n n n 与高度 h h h 的关系: n = 2 h − 1 n = 2\^h - 1 n=2h−1 ,则 h = log 2 ( n + 1 ) h = \\log_2(n+1) h=log2(n+1)代入上式得: T ( n ) = n − log 2 ( n + 1 ) ≈ n T(n) = n - \\log_2(n+1) \\approx n T(n)=n−log2(n+1)≈n因此:建堆的时间复杂度为 O ( N ) O(N) O(N)。
*** ** * ** ***
##### 堆的插入
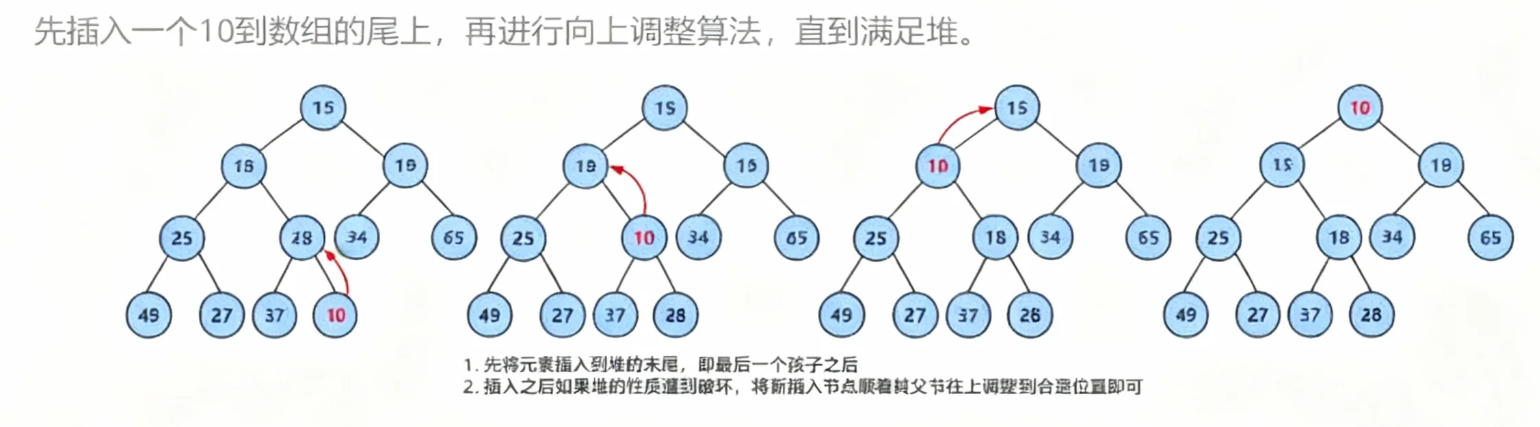
**核心:** 向上调整算法
```c
void HPPush(HP* php, HPDataType x) {
assert(php);
// 扩容检查
if (php->size == php->capacity) {
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->arr, sizeof(HPDataType) * newCapacity);
if (tmp == NULL) {
perror("realloc fail");
return;
}
php->arr = tmp;
php->capacity = newCapacity;
}
// 插入并向上调整
php->arr[php->size] = x;
php->size++;
AdjustUp(php, php->size - 1);
}
```
##### 堆的删除
**核心:** 向下调整算法
```c
void HPPop(HP* php) {
assert(php && !HPEmpty(php));
// 将堆顶与最后一个元素交换,删除最后一个,再向下调整
Swap(&php->arr[0], &php->arr[php->size - 1]);
php->size--;
AdjustDown(php, 0);
}
```
##### 取堆顶的数据
```c
HPDataType HPTop(HP* php) {
assert(php && !HPEmpty(php));
return php->arr[0];
}
```
##### 堆的数据个数
```c
int HPSize(HP* php) {
assert(php);
return php->size;
}
```
🚩要注意这里的**返回值`int`** ,不是堆数据中的`HPDataType`
*** ** * ** ***
##### 堆的判空
```c
bool HPEmpty(HP* php) {
assert(php);
return php->size == 0;
}
```
*** ** * ** ***
##### 堆的遍历打印
```c
void HPPrint(HP* php) {
for (int i = 0; i < php->size; i++) {
printf("%d ", php->arr[i]);
}
printf("\n");
}
```
*** ** * ** ***
## test.c
🚩这里展示了**如何用同一套代码创建不同性质的堆**
```c
#include "Heap.h"
int main() {
HP minHeap;
HP maxHeap;
int data[] = { 65, 100, 70, 32, 50, 60 };
int n = sizeof(data) / sizeof(data[0]);
// -------------------------------------------
// 场景 1:建立小根堆 (Min Heap)
// -------------------------------------------
printf("=== 测试小根堆 (Min Heap) ===\n");
HPInit(&minHeap, HP_Less); // 传入 Less 策略
for (int i = 0; i < n; i++) {
HPPush(&minHeap, data[i]);
}
printf("底层数组结构: ");
HPPrint(&minHeap); // 预期: 32 50 60 100 65 70 (类似结构)
printf("依次取堆顶: ");
while (!HPEmpty(&minHeap)) {
printf("%d ", HPTop(&minHeap)); // 预期: 32 50 60 65 70 100 (升序)
HPPop(&minHeap);
}
printf("\n\n");
HPDesTroy(&minHeap);
// -------------------------------------------
// 场景 2:建立大根堆 (Max Heap)
// -------------------------------------------
printf("=== 测试大根堆 (Max Heap) ===\n");
HPInit(&maxHeap, HP_Greater); // 传入 Greater 策略
for (int i = 0; i < n; i++) {
HPPush(&maxHeap, data[i]);
}
printf("底层数组结构: ");
HPPrint(&maxHeap); // 预期: 100 65 70 32 50 60 (类似结构)
printf("依次取堆顶: ");
while (!HPEmpty(&maxHeap)) {
printf("%d ", HPTop(&maxHeap)); // 预期: 100 70 65 60 50 32 (降序)
HPPop(&maxHeap);
}
printf("\n");
HPDesTroy(&maxHeap);
return 0;
}
```
*** ** * ** ***
## 堆的应用
##### 堆排序
> 🔗[Lucy的空间骇客裂缝:堆排序](https://blog.csdn.net/fengtinghuqu520/article/details/156472262?spm=1011.2415.3001.5331)
*** ** * ** ***
##### TOP-K问题
> 🔗[Lucy的空间骇客裂缝:TOP-K问题](https://blog.csdn.net/fengtinghuqu520/article/details/156472658?spm=1011.2415.3001.10575&sharefrom=mp_manage_link)
*** ** * ** ***
## 堆(Heap)精选题解析:判定、建堆与删除
### 题目一:堆的判定
**题目描述:**
下列关键字序列为堆的是:( )
A. 100, 60, 70, 50, 32, 65
B. 60, 70, 65, 50, 32, 100
C. 65, 100, 70, 32, 50, 60
D. 70, 65, 100, 32, 50, 60
E. 32, 50, 100, 70, 65, 60
F. 50, 100, 70, 65, 60, 32
**正确答案:A**
#### 💡 详细解析
首先回归堆的定义:
* **大根堆** :父节点的值 ≥ \\ge ≥ 子节点的值。
* **小根堆** :父节点的值 ≤ \\le ≤ 子节点的值。
* **物理结构** :数组;**逻辑结构**:完全二叉树。
* **下标关系** :对于下标 i i i(从0开始),左孩子是 2 i + 1 2i+1 2i+1,右孩子是 2 i + 2 2i+2 2i+2。
**逐个分析选项:**
* **A选项:** `100, 60, 70, 50, 32, 65`
* 根(100) ≥ \\ge ≥ 左(60) \& 右(70) ✅
* 节点(60) ≥ \\ge ≥ 左(50) \& 右(32) ✅
* 节点(70) ≥ \\ge ≥ 左(65) ✅
* **结论:** 这是一个标准的**大根堆**。
* **B选项:** 根 60 \< 左 70。若为小堆,70 的孩子是 50,70 \> 50 违背性质。 ❌
* **C选项:** 根 65 \< 左 100。若为小堆,100 的孩子是 32,100 \> 32 违背性质。 ❌
* **E选项:** 根 32,左右 50, 100。看似小堆,但 100 的孩子是 60,100 \> 60 违背性质。 ❌
*** ** * ** ***
### 题目二:堆删除操作的比较次数
**题目描述:**
已知小根堆为 `8, 15, 10, 21, 34, 16, 12`,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是 ( )。
A. 1 B. 2 C. 3 D. 4
**正确答案:C**
#### 💡 详细解析
这是考察**向下调整算法 (AdjustDown)** 细节的经典题。
**1. 初始交换与删除**
将堆顶(8)与堆尾(12)交换,删除8。
* 此时数组:`[12, 15, 10, 21, 34, 16]`
**2. 向下调整过程(记录比较)**
* **第一次比较** :比较左孩子 15 和右孩子 10。 10 \< 15 10 \< 15 10\<15,选出**最小孩子 10**。
* **第二次比较** :比较父节点 12 和最小孩子 10。 12 \> 10 12 \> 10 12\>10,**不满足小堆,交换** 。
* 此时数组:`[10, 15, 12, 21, 34, 16]`
* **第三次比较** :此时父节点 12 来到原 10 的位置(下标2)。其左孩子为 16(下标5),无右孩子。比较父节点 12 和左孩子 16。 12 \< 16 12 \< 16 12\<16,**满足小堆,停止**。
**总结:** 总计比较 **3** 次。
*** ** * ** ***
### 题目三:堆排序的初始建堆
**题目描述:**
一组记录排序码为 `(5, 11, 7, 2, 3, 17)`,则利用堆排序方法建立的初始堆为:
A. (11, 5, 7, 2, 3, 17)
C. (17, 11, 7, 2, 3, 5)
*(注:原题选项 A 可能存在争议,此处重点对比标准建堆过程)*
#### 💡 详细解析
通常堆排序用于升序时,建立的是**大根堆** 。采用 **Floyd 建堆算法(筛选法)** :从最后一个非叶子节点 ( n / 2 − 1 ) (n/2-1) (n/2−1) 开始向前调整。
**序列:** `[5, 11, 7, 2, 3, 17]`,长度 n = 6 n=6 n=6。
1. **调整下标 2 (值7)** :孩子是 17。 7 \< 17 7 \< 17 7\<17,交换。
* 变为:`[5, 11, 17, 2, 3, 7]`
2. **调整下标 1 (值11)** :孩子是 2, 3。 11 \> 3 11 \> 3 11\>3,无需交换。
3. **调整下标 0 (值5)** :孩子是 11, 17。
* 先比较孩子: 17 \> 11 17 \> 11 17\>11;再与父比较: 17 \> 5 17 \> 5 17\>5,交换。
* 变为:`[17, 11, 5, 2, 3, 7]`
* **继续向下调整 5** :孩子是 7。 7 \> 5 7 \> 5 7\>5,交换。
* **最终结果** :`[17, 11, 7, 2, 3, 5]`(对应选项 C)
> **⚠️ 争议点点拨** :
>
> 若某些题库答案为 A,通常是因为其采用了"从前往后插入"的非标准建堆方式,或者题目数据/选项存在印刷错误。在标准考试中,请务必掌握 **C (筛选法)** 的推导。
*** ** * ** ***
### 题目四:最小堆的删除结果
**题目描述:**
最小堆 `[0, 3, 2, 5, 7, 4, 6, 8]`,在删除堆顶元素 0 之后,其结果是 ( )
A. \[3, 2, 5, 7, 4, 6, 8
B. [2, 3, 5, 7, 4, 6, 8]
C. [2, 3, 4, 5, 7, 8, 6]
D. [2, 3, 4, 5, 6, 7, 8]
正确答案:C
💡 详细解析
1. 初始状态
逻辑结构如下:
0
2
3
4
5
6
7
8
💻结尾--- 核心连接协议
警告: 🌠🌠正在接入底层技术矩阵。如果你已成功破解学习中的逻辑断层,请执行以下指令序列以同步数据:🌠🌠
【📡】 建立深度链接: 关注本终端。在赛博丛林中深耕底层架构,从原始代码到进阶协议,同步见证每一次系统升级。
【⚡】 能量过载分发: 执行点赞操作。通过高带宽分发,让优质模组在信息流中高亮显示,赋予知识跨维度的传播力。
【💾】 离线缓存核心: 将本页加入收藏。把这些高频实战逻辑存入你的离线存储器,在遭遇系统崩溃或需要离线检索时,实现瞬时读取。
【💬】 协议加密解密: 在评论区留下你的散列码。分享你曾遭遇的代码冲突或系统漏洞(那些年踩过的坑),通过交互式编译共同绕过技术陷阱。
【🛰️】 信号频率投票: 通过投票发射你的选择。你的每一次点击都在重新定义矩阵的进化方向,决定下一个被全量拆解的技术节点。




