二叉排序树的建立和插入

（一）.二叉排序树是很关键的，二叉排序树的构造是根节点比左子树上的所有值要大，比右子树上的值都有小，二叉排序树中的所有子树都是这样的性质，可以和二叉树的中序遍历联系起来，二叉树的中序遍历是左根右，按照上述所说的，二叉树排序树的中序遍历是有序地递增的，这篇文章就证明一下二叉树排序树的中序遍历是有序的。

1.首先构建一个结构体类型，和二叉树一样，有左右孩子指针，一个数据域

复制代码

typedef struct BSTNode
{
	int data;
	struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;//第二个重命名的是个指针

2.创建一个数组，利用数组个二叉排序树赋值，其主要思想就是二叉排序树的插入操作，其中比较坑的一点是插入时递归，需要弄清楚为什么不用链接到新开辟的节点。创建一个creat_BST函数，将值一个一个插入到二叉排序树，插入操作使用是递归，其中前两个条件是结束递归的终止条件，不可以缺少，二叉排序树中不能有重复的数字，传入的是二级指针，对二级指针解引用可以改变值，当传入的这个关键字比节点值小就要沿着左边孩子对比，反之就是向着右边孩子对比。

复制代码

int insert_BST(BSTree* T, int k)
{
	if (*(T) == NULL)//终止条件
	{
		(*T) = (BSTNode*)malloc(sizeof(BSTNode));
		if ((*T) == NULL)
			return 1;

		(*T)->data = k;
		(*T)->lchild = (*T)->rchild = NULL;
		return 1;
	}
	if ((*T)->data == k)//终止条件
		return 0;
	else if ((*T)->data < k)
	{
		return insert_BST(&((*T)->rchild), k);//传入右边孩子
	}
	else
	{
		return insert_BST(&((*T)->lchild), k);
	}
}
void creat_BST(BSTree*T,int arr[], int sz)
{
	(*T) = NULL;
	for (int i = 0; i < sz; i++)
	{
		insert_BST(T, arr[i]);
	}
}

3.二叉排序树的中序遍历

复制代码

void print(BSTree T)
{
	if (T == NULL)
		return;
	print(T->lchild);
	printf("%d ", T->data);
	print(T->rchild);
}

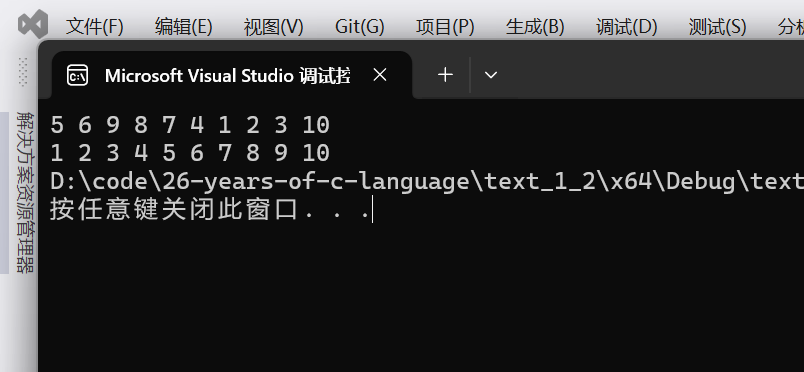
传入 5 6 9 8 7 4 1 2 3 10 构建的二叉排序树图片应该是这样的，中序遍历是这样的，满足有序递增。

（二）.整体代码

复制代码

typedef struct BSTNode
{
	int data;
	struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;//第二个重命名的是个指针

int insert_BST(BSTree* T, int k)
{
	if (*(T) == NULL)//终止条件
	{
		(*T) = (BSTNode*)malloc(sizeof(BSTNode));
		if ((*T) == NULL)
			return 1;

		(*T)->data = k;
		(*T)->lchild = (*T)->rchild = NULL;
		return 1;
	}
	if ((*T)->data == k)//终止条件
		return 0;
	else if ((*T)->data < k)
	{
		return insert_BST(&((*T)->rchild), k);//传入右边孩子
	}
	else
	{
		return insert_BST(&((*T)->lchild), k);
	}
}
void creat_BST(BSTree*T,int arr[], int sz)
{
	(*T) = NULL;
	for (int i = 0; i < sz; i++)
	{
		insert_BST(T, arr[i]);
	}
}
void print(BSTree T)
{
	if (T == NULL)
		return;
	print(T->lchild);
	printf("%d ", T->data);
	print(T->rchild);
}
int main()
{
	BSTree T;
	int arr[10] = { 0 };
	int i = 0;
	int sz = sizeof(arr) / sizeof(arr[0]);
	for (i = 0; i < sz; i++)
	{
		scanf("%d", &arr[i]);
	}
	creat_BST(&T,arr, sz);
	print(T);
}