亚毫米波FMCW脉冲多普勒雷达:粒子云动态特性表征技术深度解析
T. Bryllert, M. Bonmann and J. Stake, "A Submillimeter-Wave FMCW Pulse-Doppler Radar to Characterize the Dynamics of Particle Clouds," in IEEE Transactions on Terahertz Science and Technology, vol. 13, no. 4, pp. 389-395, July 2023, doi: 10.1109/TTHZ.2023.3263641.
引言与研究背景
在制药工业和流化床燃烧反应器等众多工业应用中,粒子或粉末分散在工艺反应器中的动态行为对于维持工艺质量和深入理解工艺过程至关重要。传统的测量方法往往需要将物理探针插入反应器内部,这不仅会改变工艺过程本身,在某些恶劣的工艺环境中更是难以实现。因此,以高更新率和高空间分辨率实现非接触式的粒子浓度和局部粒子速度测量成为了一个迫切的技术需求。
本文介绍的是由瑞典查尔姆斯理工大学太赫兹与毫米波实验室的Tomas Bryllert、Marlene Bonmann和Jan Stake三位研究者开发的340 GHz调频连续波(FMCW)脉冲多普勒雷达系统。该系统发表于IEEE Transactions on Terahertz Science and Technology 2023年7月刊,代表了亚毫米波雷达技术在工业应用领域的重要进展。该收发模块具有约1 mW的输出功率和超过30 GHz的带宽,前端光学系统由收发单元的喇叭天线馈电的离轴抛物面镜组成,产生准直的雷达波束。
与使用可见光或红外光的其他非接触式测量方法相比,亚毫米波段具有几个显著优势。首先,亚毫米波能够更深入地穿透致密粒子云,对反应器观察窗上的污染物也不那么敏感。其次,雷达技术允许进行多普勒处理,从而揭示粒子的速度信息。与更传统的微波和毫米波雷达技术相比,亚毫米波具有以下几个有利特性:短波长使得检测更小粒子成为可能,因为在瑞利散射区域内雷达截面积与波长的四次方成反比(σ ∝ λ⁻⁴);宽带宽带来更高的距离分辨率,例如30 GHz带宽理论上可实现5 mm的距离分辨率;对于固定天线尺寸(通常受实际应用中观察窗尺寸限制),衍射极限分辨率随波长减小而提高,因此高频时横向分辨率更优。
已有多个中心频率超过300 GHz的高分辨率三维成像FMCW雷达被报道。基于SiGe技术的MMIC收发器FMCW雷达也在毫米波段得到了验证,甚至在480 GHz展示了有前途的性能。然而,室温下具有高动态范围的亚毫米波收发器仍然需要二极管技术。使用距离-多普勒处理的亚毫米波FMCW雷达------即不仅能测量距离还能测量目标速度的雷达------非常罕见。Cooper等人报道了一个660 GHz的FMCW距离-多普勒雷达系统,证明了距离-多普勒概念在亚毫米波频率的可行性,但关于对不同目标的灵敏度或距离-多普勒图像中噪声底限的来源细节很少。
雷达系统架构
系统总体设计
图1展示了整个雷达系统的实物照片。前端光学器件和电子设备安装在一个底板上,连同模拟和数字基带电路一起构成了一个紧凑的三脚架安装式设计。系统的整体尺寸约为45 cm × 30 cm,这种紧凑的形式因素使其能够方便地部署在各种工业场景中。该收发模块最初是为Wasa Millimeter Wave AB开发的16通道高帧率成像雷达设计的。

电子硬件架构
图2给出了340 GHz FMCW脉冲多普勒雷达的系统框图。整个系统采用频率上变频和频率倍增的FMCW雷达架构。在发射端,数字波形发生器是一块FPGA控制的任意波形卡(Analog Devices公司的ADS7-V2EBZ),具有4 Gb的可用内存和超过6 Gs/s的最大采样率,本工作中使用4 Gs/s。该卡能够直接从内存写入超过100 ms的1 GHz带宽波形数据,这意味着在一个相干脉冲多普勒处理间隔(CPI)内------通常远短于100 ms------可以发射任意的FMCW脉冲串并重复。多个FMCW波形因此可以在一个相干处理间隔内交织,分别针对系统带宽(323-357 GHz)的不同部分,从而高效地提取场景的频率分辨(光谱)信息,尽管这一功能在本文展示的性能演示中未被使用。
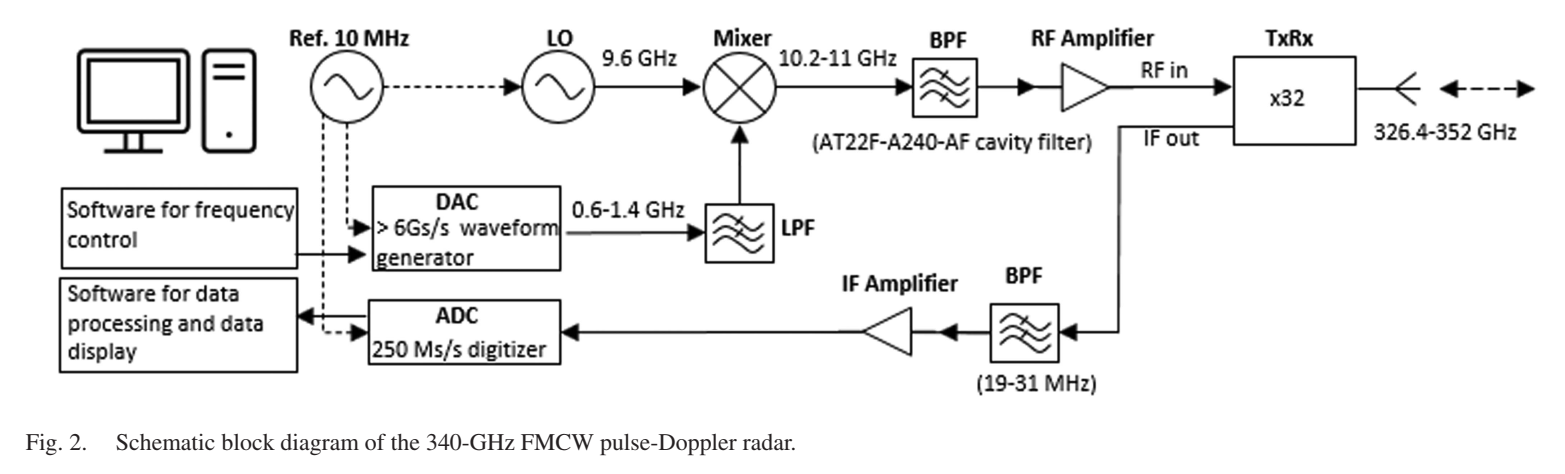
基带啁啾信号通常为1 GHz带宽,由数字硬件生成并以1 GHz为中心。该信号通过混频器和9.6 GHz本振上变频到X波段(10.2-11 GHz范围),经过带通滤波器(AT22F-A240-AF腔体滤波器)和RF放大器后传递给收发模块。前端的340 GHz肖特基二极管电路设计为同时作为二倍频器(×2)和次谐波混频器工作,从而同时实现发射和接收功能。收发模块的本振链由Gotmic AB开发的InGaAs pHEMT有源八倍频器MMIC(×8)和170 GHz肖特基二极管倍频器组成。GaAs肖特基势垒二极管电路在查尔姆斯理工大学的纳米制造实验室制造。最终,收发单元将X波段啁啾信号倍频32倍,产生总带宽为32 GHz、中心频率约340 GHz(覆盖326.4-352 GHz)的发射信号。雷达回波在收发器中接收,并使用平衡配置直接与发射信号混频降至基带。
光学系统与天线
收发单元输出端使用Custom Microwave Inc.的圆形喇叭天线作为光学系统的馈源。该馈源喇叭照射一面来自Edmund Optics的4英寸(约10 cm)离轴抛物面镜,有效焦距为6英寸(约15 cm),光学系统产生准直的雷达波束。这种光学配置的优点是可以在较长距离上保持较小的波束宽度,从而实现良好的横向分辨率。
接收端数字硬件
接收端的数字硬件包括一块来自National Instruments的八通道250 Ms/s数字化仪(使用一个通道),具有14位分辨率。数字化仪由FPGA控制,提供确定性的时序控制。数字化卡(PXIe格式)通过PXIe总线与PC控制器集成,实现实时信号处理和显示。波形卡、模数转换器(ADC)和本振共用一个10 MHz参考源,形成一个完全相干的系统------这对于脉冲多普勒处理至关重要,因为多普勒处理依赖于脉冲间的相位相干性。
雷达信号处理与理论分析
关键雷达参数
本工作中使用的典型雷达参数包括:中心频率fc=340f_c = 340fc=340 GHz,脉冲带宽BW=32BW = 32BW=32 GHz,脉冲时间tp=41t_p = 41tp=41 μs,脉冲重复间隔PRI=102.4\text{PRI} = 102.4PRI=102.4 μs或51.2 μs,相干处理的脉冲数nPRI=128n_{\text{PRI}} = 128nPRI=128,目标距离R=4R = 4R=4至6 m。
这些参数决定了最大不模糊距离(RmaxR_{\max}Rmax)和最大不模糊速度(vmaxv_{\max}vmax)的理论极限,以及距离和速度分辨率。设ccc为空气中的光速,最大不模糊距离为:
Rmax=PRI×c2≈15 kmR_{\max} = \frac{\text{PRI} \times c}{2} \approx 15 \text{ km}Rmax=2PRI×c≈15 km
最大不模糊速度由脉冲重复频率和载波频率共同决定:
vmax=c2×PRI×fc=4.3 m/sv_{\max} = \frac{c}{2 \times \text{PRI} \times f_c} = 4.3 \text{ m/s}vmax=2×PRI×fcc=4.3 m/s
距离分辨率由带宽决定:
ΔR=c2×BW=3×1082×32×109=5 mm\Delta R = \frac{c}{2 \times BW} = \frac{3 \times 10^8}{2 \times 32 \times 10^9} = 5 \text{ mm}ΔR=2×BWc=2×32×1093×108=5 mm
这也是在距离FFT中不使用零填充时的距离单元大小。
多普勒处理与速度分辨率
在多普勒维度上,频率分辨率(ΔfD\Delta f_DΔfD)由相干积分时间(tc=PRI×nPRIt_c = \text{PRI} \times n_{\text{PRI}}tc=PRI×nPRI)决定。对于本系统,相干积分时间为:
tc=102.4 μs×128=13.1 mst_c = 102.4 \text{ μs} \times 128 = 13.1 \text{ ms}tc=102.4 μs×128=13.1 ms
因此频率分辨率为:
ΔfD=1tc=113.1×10−3≈76.3 Hz\Delta f_D = \frac{1}{t_c} = \frac{1}{13.1 \times 10^{-3}} \approx 76.3 \text{ Hz}ΔfD=tc1=13.1×10−31≈76.3 Hz
通过多普勒关系式fD=2v/λf_D = 2v/\lambdafD=2v/λ(其中vvv是目标的径向速度,λ=c/fc≈0.88\lambda = c/f_c \approx 0.88λ=c/fc≈0.88 mm),频率分辨率转换为速度分辨率:
Δv=ΔfD×λ2=1tc×λ2=1tc×c2fc=3.8 cm/s\Delta v = \Delta f_D \times \frac{\lambda}{2} = \frac{1}{t_c} \times \frac{\lambda}{2} = \frac{1}{t_c} \times \frac{c}{2f_c} = 3.8 \text{ cm/s}Δv=ΔfD×2λ=tc1×2λ=tc1×2fcc=3.8 cm/s
信号处理流程
图3展示了数字信号处理的流程框图。相干处理的数据矩阵格式为(ns)×(nPRI)(n_s) \times (n_{\text{PRI}})(ns)×(nPRI),即每脉冲采样数乘以脉冲数。收发器下变频后,接收的基带中频(IF)信号首先通过19-31 MHz的模拟带通滤波器,匹配感兴趣的目标距离范围(对应约2.85-4.65 m的距离范围,考虑到FMCW雷达中拍频与距离的线性关系)。
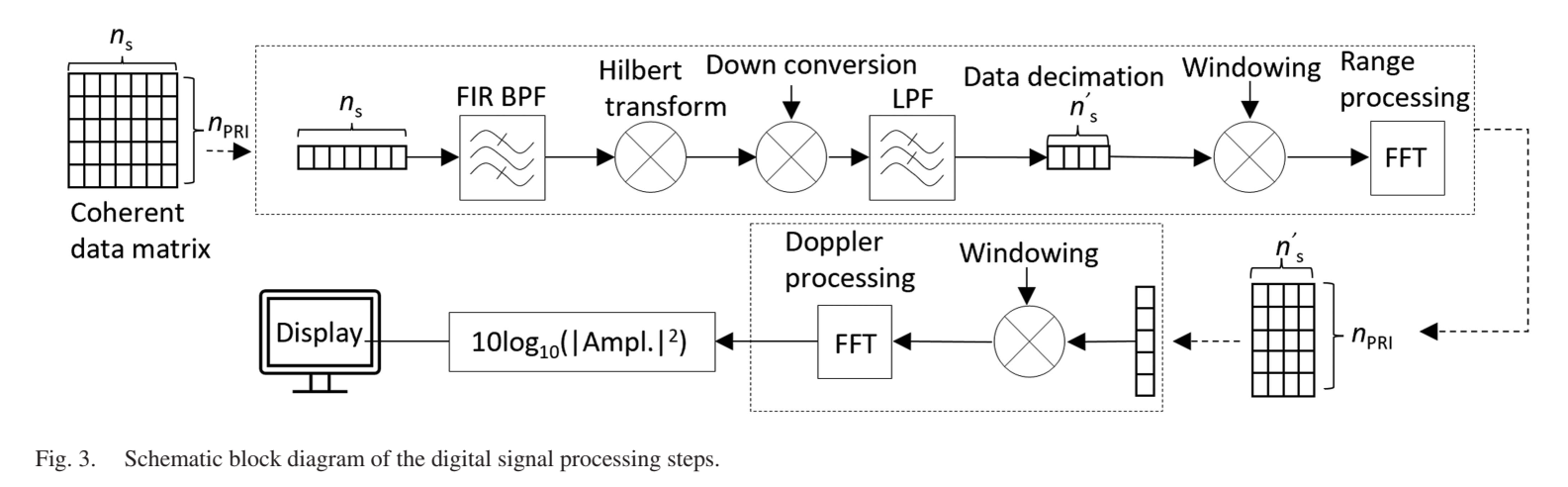
信号随后被数字化,经过20-30 MHz的数字FIR带通滤波,借助希尔伯特变换转换为IQ(同相/正交)格式,下变频至复基带,并以16倍抽取至1.5倍奈奎斯特极限采样(15.625 Ms/s IQ),此时ns′=640n'_s = 640ns′=640。实际上,由于低频振铃效应,每个波形开头和结尾的若干采样点被丢弃,留下590个采样点而非640个,这也将有效使用带宽从32 GHz降至29.5 GHz。
FMCW脉冲多普勒雷达的一个重要特性是距离压缩和多普勒处理都可以通过傅里叶变换完成。这意味着信号处理可以通过对相干数据矩阵进行二维FFT来实现------沿快时间(采样)维度的FFT实现距离压缩,沿慢时间(脉冲)维度的FFT实现多普勒处理。为了减少频谱泄漏和旁瓣,在两个维度都应用汉宁窗函数。雷达用户看到的输出是距离-多普勒图中雷达信号幅度平方的对数,即10log10(∣Ampl∣2)10\log_{10}(|\text{Ampl}|^2)10log10(∣Ampl∣2)。
自由落体验证模型
为了验证速度测量能力,研究者将已知直径(10 mm)和重量(m=4m = 4m=4 g)的自由落体金属球的测量位置和速度与成熟的解析自由落体模型进行了比较。让金属球朝向雷达下落,它在重力和二次空气阻力(∝v2\propto v^2∝v2)作用下垂直运动。求解牛顿第二运动定律,速度vvv和位置xxx随时间ttt的变化可描述为:
v=vttanh(t/τ)(1a)v = v_t \tanh(t/\tau) \tag{1a}v=vttanh(t/τ)(1a)
x=x0−vtτln(cosh(t/τ))(1b)x = x_0 - v_t \tau \ln(\cosh(t/\tau)) \tag{1b}x=x0−vtτln(cosh(t/τ))(1b)
其中终端速度为:
vt=2mgAρaircdv_t = \sqrt{\frac{2mg}{A\rho_{\text{air}}c_d}}vt=Aρaircd2mg
特征时间为τ=vt/g\tau = v_t/gτ=vt/g。这里ggg是地球重力加速度,mmm是金属球质量,ρair\rho_{\text{air}}ρair是常温常压下的空气密度,AAA是金属球的横截面积(A=πr2A = \pi r^2A=πr2,其中rrr为球体半径),cdc_dcd是阻力系数(对于球体在亚音速流动中取0.47),x0x_0x0是初始位置。
实验结果与性能表征
噪声性能分析
为了研究距离-多普勒图中零多普勒和有限多普勒频率处噪声底限的来源,研究者在四种不同硬件配置下进行了无目标噪声测量:仅ADC;ADC加IF放大器;ADC、IF放大器加10.1 GHz连续波信号驱动收发器;ADC、IF放大器加啁啾信号驱动收发器。
图4展示了不同硬件配置下的噪声底限,以及距离-多普勒图中不同切片的情况。图4(a)给出了噪声底限的总体视图,并标出了图4(b-d)中切片的位置。图4(b)是恒定距离切片,显示噪声随速度的变化;图4©是零多普勒处的恒定速度切片;图4(d)是有限多普勒处的恒定速度切片。
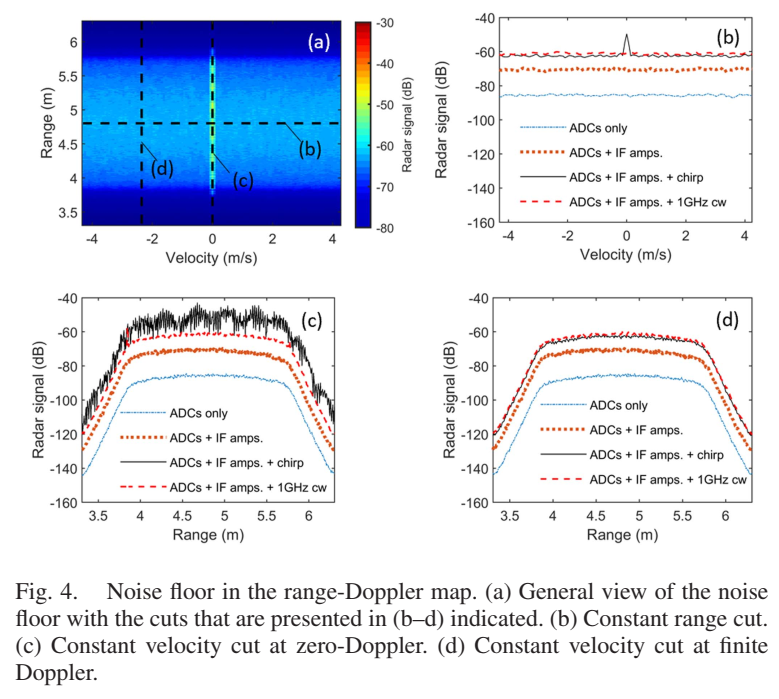
理想情况下,整个距离-多普勒图中的噪声底限应由热噪声决定,并受前端电子设备的损耗和噪声系数影响,再由中频放大进行缩放。然而,收发单元为了简化设计而牺牲了一定的噪声性能。使用同一对平衡肖特基二极管电路同时进行最后一级倍频和次谐波零差下变频,虽然使收发单元相当紧凑,但代价是产生了额外噪声。额外噪声有两种形式:次谐波混频中的转换损耗比专用混频器更差;来自本振(FMCW啁啾)的过量幅度调制噪声混入收发器的中频端(尽管使用了平衡配置)。此外,图4©显示使用短脉冲(40 μs)高带宽啁啾驱动射频硬件会在零多普勒处产生额外噪声,这一现象在其他文献中也有观察到。不过,额外噪声的代价是可以接受的,因为在评估的应用场景中信噪比通常是足够的。
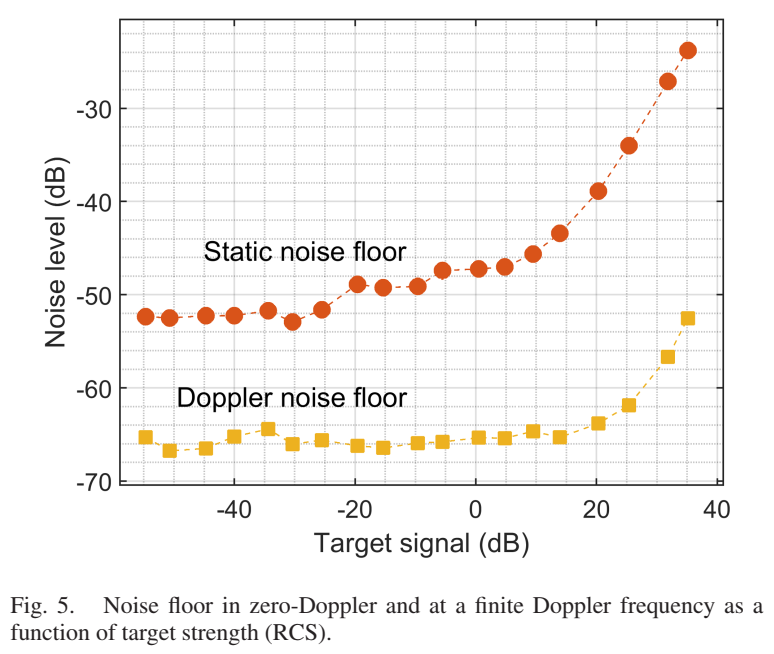
图5展示了零多普勒和有限多普勒处的噪声底限如何受静态目标强度(RCS)的影响。不同的RCS值通过将角反射器放置在雷达波束的不同位置来实现。噪声底限计算为在中频滤波器带宽内相关距离单元上的平均值(排除包含目标响应的距离单元)。零多普勒处的噪声底限(图中标注为"Static noise floor")不是随机噪声,而是由旁瓣、波形的幅度/相位调制以及射频硬件中的多次反射造成的。这些效应在有限多普勒频率处(图中标注为"Doppler noise floor")看不到,因为旁瓣/调制/反射模式在脉冲间是相同的,因此只出现在零多普勒单元中。在强目标回波时(目标信号超过约0 dB),有限多普勒频率处的噪声底限会增加,表现为整个距离-多普勒平面噪声底限的普遍上升------这表明该噪声增加源于射频载波的实际噪声。
相干积分增益验证
图6展示了静态目标(角反射器)的雷达信号和噪声底限与每CPI脉冲数(nPRIn_{\text{PRI}}nPRI)的关系。测试了nPRI=16,32,64,128,256,512n_{\text{PRI}} = 16, 32, 64, 128, 256, 512nPRI=16,32,64,128,256,512六种情况。理论上,在其他雷达参数固定的情况下,增加每CPI的脉冲数时,如果目标和雷达系统保持相干且噪声与雷达信号不相关,则目标的信噪比应线性增加(以分贝计,每倍增脉冲数增加约3 dB)。
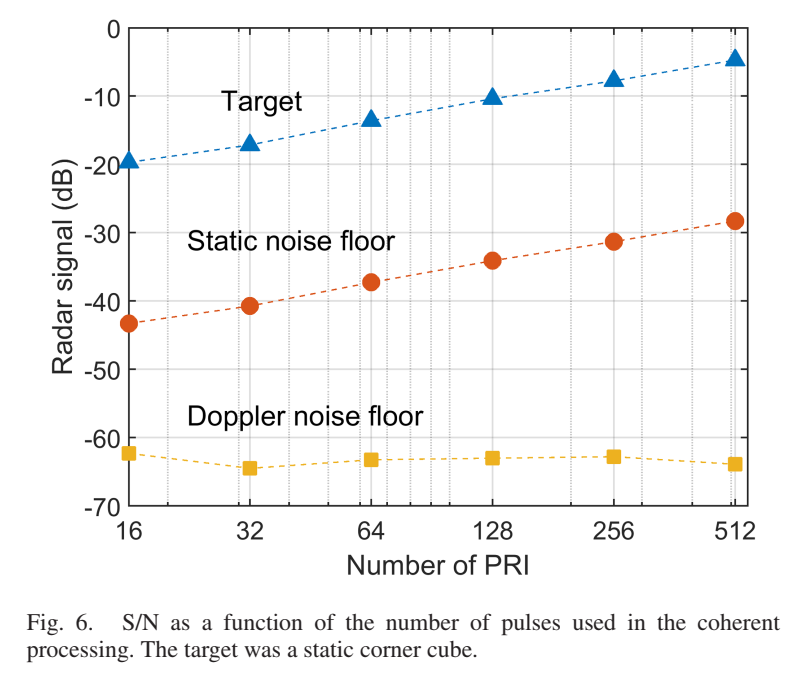
实验结果显示,当与多普勒噪声底限比较时,信噪比如预期般线性增加,从而验证了目标和雷达系统保持相干且噪声与雷达信号不相关。目标信号(图中上方曲线)和多普勒噪声底限(图中下方曲线)都随脉冲数增加而上升,但两者之间的差值------即信噪比------保持线性增长关系。如前所述,零多普勒处的噪声(静态噪声底限,图中中间曲线)源于雷达信号本身而非随机噪声,这意味着在更长的积分时间下零多普勒处的信噪比没有改善。
距离分辨率演示
为了演示雷达系统的距离分辨率,研究者将三个直径2 mm的金属珠粘在一根绳子上,放置在5 m距离处。目标的定向使得所有珠子都被雷达波束照射,且在距离方向上间隔约3 cm。图7(a-c)显示,三个金属珠在雷达测量中清晰分离,信号峰值间隔测量为3 cm和3.1 cm,可见度约20 dB信噪比。
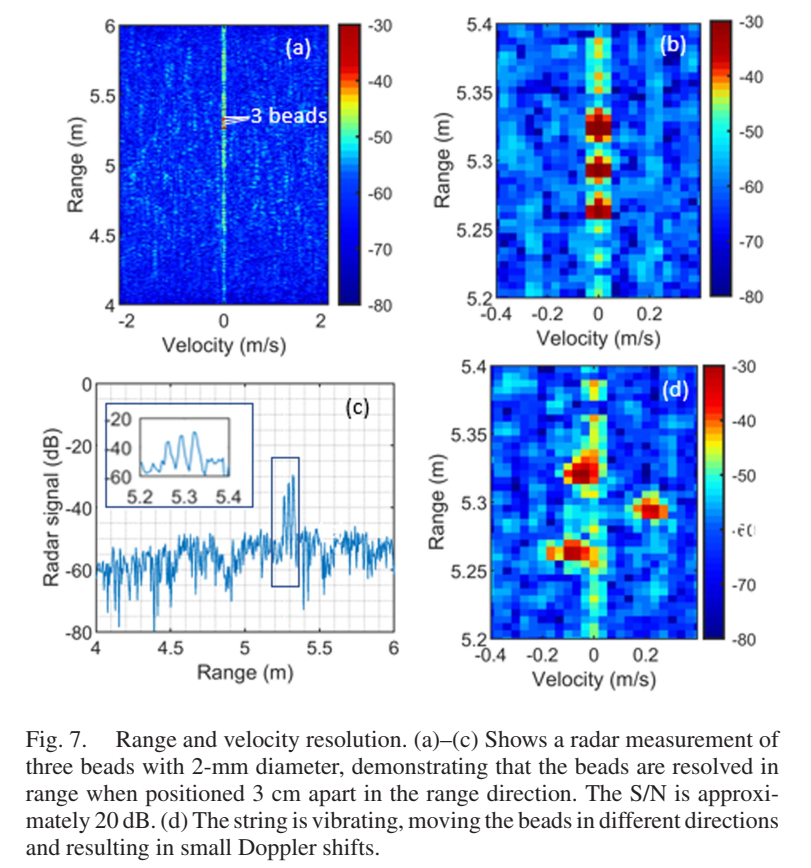
尽管珠子只有2 mm大小(远小于5 mm的理论距离分辨率),但它们在雷达图像中跨越多个距离单元,主要原因是信号处理中使用的汉宁窗在距离和多普勒维度都造成了频谱展宽。窗函数减少了频谱泄漏和旁瓣(如图7(a)所示的干净背景),但代价是展宽了多普勒和距离上的主瓣宽度约2倍。
图7(d)展示了速度分辨率的演示。当轻轻敲击绳子使其振动时,由于0.04 m/s每多普勒单元的精细多普勒分辨率,珠子在多普勒维度上也能分离------不同珠子因振动模式不同而具有不同的瞬时速度,从而产生不同的多普勒频移。
小粒子检测能力
为了研究雷达系统检测小粒子的能力,雷达波束通过一面平面金属镜折叠后垂直向上指向。一个透明塑料盒放置在折叠镜正上方用于收集粒子,这样不同的测试材料可以直接落入雷达波束中。实验使用了四种测试材料:直径10 mm的金属球、直径2 mm的金属珠、直径约500 μm的石英砂粒和直径约100 μm的球形玻璃珠。
图8(a)和(b)展示了用于测试的材料照片,可以清楚看到不同材料的尺寸差异。对于每种材料,图8(c-f)显示了多个CPI积分后的相应距离-多普勒图。这种时间积分显示方式允许观察粒子的完整运动轨迹。

图8©显示了直径10 mm金属球的下落轨迹。可以清楚看到金属球朝向雷达加速的过程------随着下落距离增加,速度(负多普勒值表示朝向雷达运动)也在增加。每个亮点对应一个单独的CPI或雷达"帧",帧率为6.2帧/秒(1/(nPRI×PRI)=1/(128×102.4 μs)1/(n_{\text{PRI}} \times \text{PRI}) = 1/(128 \times 102.4 \text{ μs})1/(nPRI×PRI)=1/(128×102.4 μs))。图中叠加了由自由落体模型(公式1)预测的轨迹曲线,可以看出测量结果与理论预测非常吻合,从而有力地支持了雷达速度测量的准确性。
图8(d)显示了直径2 mm金属珠的类似测量结果,尽管回波强度较弱(由于更小的RCS),但轨迹仍然清晰可见。图8(e)展示了几撮直径500 μm砂粒的积分图像。值得注意的是,图中可以清晰地检测到单个砂粒的回波。在4.3 m距离处,砂粒撞击塑料盒并弹跳至静止。从塑料盒的偏转表现为正多普勒速度(远离雷达运动),在图中零速度线上方可见。图8(f)显示了最小的测试粒子------直径100 μm玻璃球的检测结果。虽然单个粒子的回波较弱,但多次投放粒子后积分的粒子流清晰可见。
总之,所有测试材料都能在5 m距离处以显著的信噪比被检测到,证明了该雷达仪器适用于监测粒子云动态。约1 cm的距离分辨率和几厘米的横向分辨率(3 dB波束宽度)使得可以用几立方厘米的测量体素来表征粒子云的动态特性。
与其他亚毫米波雷达的比较
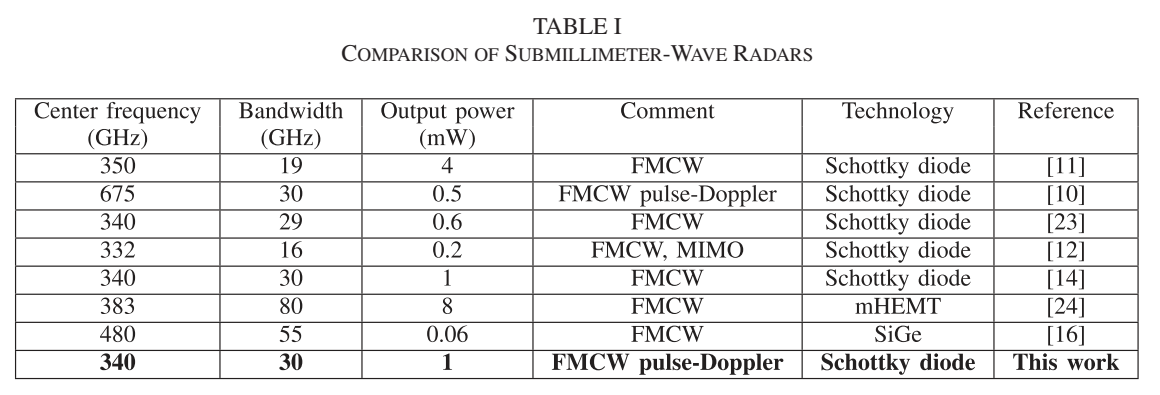
表I比较了多个亚毫米波雷达在中心频率、带宽、输出功率和技术方面的规格。比较的系统包括:660 GHz系统(3 GHz带宽)、350 GHz系统(28.8 GHz带宽)、580 GHz系统(30 GHz带宽)、400 GHz系统(40 GHz带宽)以及本文的340 GHz系统(30 GHz带宽)。
本文介绍的雷达系统与大多数其他系统具有可比的带宽,即距离分辨率。技术路线上,高频系统(如660 GHz和580 GHz)采用亚谐波肖特基混频器,而本系统和400 GHz系统采用倍频加混频的收发架构。然而,只有文献[10]中的660 GHz雷达系统以距离-多普勒模式运行,其啁啾带宽为3 GHz,声称的距离和速度分辨率分别为5 cm和0.2 m/s。本工作的结果展示了显著的分辨率提升:距离分辨率约1 cm(相对于5 cm提升约5倍),速度分辨率3.8 cm/s(相对于20 cm/s提升约5倍),综合而言实现了高达十倍的分辨率改善。
结论与展望
这项工作呈现了一个340 GHz调频连续波脉冲多普勒雷达系统。数字雷达波形生成允许相干和任意的FMCW脉冲波形,雷达的性能表现与理论预测相符。系统展示了约1 cm的距离分辨率和几厘米的横向分辨率(3 dB波束宽度),速度分辨率达到3.8 cm/s。该仪器在空间域和多普勒速度方面的灵敏度和分辨率足以映射粒子云的动态特性,测量体素大小仅为几立方厘米。
这一能力通过对粒径从100 μm到10 mm范围内的自由落体粒子进行雷达测量得到了充分验证。单个直径低至500 μm的砂粒可在5 m距离处被清晰检测,100 μm玻璃球形成的粒子流也清晰可见。通过将10 mm金属球的测量轨迹与考虑空气阻力的解析自由落体模型对比,验证了速度测量的准确性。
附录:FMCW脉冲多普勒雷达数学原理
A.1 FMCW雷达基本原理
FMCW雷达发射一个频率随时间线性变化的啁啾信号。设发射信号为:
sTX(t)=ATXcos(2πfct+πBWtpt2+ϕ0)s_{\text{TX}}(t) = A_{\text{TX}} \cos\left(2\pi f_c t + \pi \frac{BW}{t_p} t^2 + \phi_0\right)sTX(t)=ATXcos(2πfct+πtpBWt2+ϕ0)
其中fcf_cfc是中心频率,BWBWBW是啁啾带宽,tpt_ptp是脉冲持续时间,ϕ0\phi_0ϕ0是初始相位。啁啾率(chirp rate)定义为:
γ=BWtp\gamma = \frac{BW}{t_p}γ=tpBW
对于本系统,γ=32 GHz/41 μs≈780 MHz/μs\gamma = 32 \text{ GHz} / 41 \text{ μs} \approx 780 \text{ MHz/μs}γ=32 GHz/41 μs≈780 MHz/μs。
当雷达信号遇到距离RRR处的目标并返回时,接收信号相对于发射信号有一个时间延迟:
τ=2Rc\tau = \frac{2R}{c}τ=c2R
接收信号可表示为:
sRX(t)=ARXcos(2πfc(t−τ)+πγ(t−τ)2+ϕ0)s_{\text{RX}}(t) = A_{\text{RX}} \cos\left(2\pi f_c (t-\tau) + \pi \gamma (t-\tau)^2 + \phi_0\right)sRX(t)=ARXcos(2πfc(t−τ)+πγ(t−τ)2+ϕ0)
在零差接收架构中,接收信号与发射信号混频,经低通滤波后得到中频(IF)信号。混频过程产生和差频成分,低通滤波器保留差频成分:
sIF(t)=AIFcos(2πfcτ+2πγτt−πγτ2)s_{\text{IF}}(t) = A_{\text{IF}} \cos\left(2\pi f_c \tau + 2\pi \gamma \tau t - \pi \gamma \tau^2\right)sIF(t)=AIFcos(2πfcτ+2πγτt−πγτ2)
忽略常数相位项πγτ2\pi \gamma \tau^2πγτ2(它不影响频率测量),中频信号是一个频率为:
fIF=γτ=BWtp⋅2Rc=2⋅BW⋅Rc⋅tpf_{\text{IF}} = \gamma \tau = \frac{BW}{t_p} \cdot \frac{2R}{c} = \frac{2 \cdot BW \cdot R}{c \cdot t_p}fIF=γτ=tpBW⋅c2R=c⋅tp2⋅BW⋅R
的正弦信号。这就是FMCW雷达的核心原理:中频频率与目标距离成正比。
由此可得距离:
R=fIF⋅c⋅tp2⋅BWR = \frac{f_{\text{IF}} \cdot c \cdot t_p}{2 \cdot BW}R=2⋅BWfIF⋅c⋅tp
A.2 距离分辨率推导
两个目标可被分辨的条件是它们产生的中频信号在频谱上可以区分。对于持续时间为tpt_ptp的信号,频率分辨率由傅里叶变换的基本性质决定:
δf=1tp\delta f = \frac{1}{t_p}δf=tp1
将频率分辨率转换为距离分辨率:
ΔR=δf⋅c⋅tp2⋅BW=c2⋅BW\Delta R = \frac{\delta f \cdot c \cdot t_p}{2 \cdot BW} = \frac{c}{2 \cdot BW}ΔR=2⋅BWδf⋅c⋅tp=2⋅BWc
这个重要结果表明距离分辨率仅取决于带宽,与脉冲持续时间无关 。对于BW=32BW = 32BW=32 GHz:
ΔR=3×1082×32×109=4.69 mm≈5 mm\Delta R = \frac{3 \times 10^8}{2 \times 32 \times 10^9} = 4.69 \text{ mm} \approx 5 \text{ mm}ΔR=2×32×1093×108=4.69 mm≈5 mm
实际上由于仅使用29.5 GHz有效带宽(舍弃边缘采样点后),实际距离分辨率约为5.1 mm。加上汉宁窗导致的主瓣展宽(约2倍),有效距离分辨率约为1 cm。
A.3 多普勒效应与速度测量
当目标以径向速度vvv运动时(朝向雷达为正),接收信号会发生多普勒频移。对于电磁波,多普勒频移为:
fD=2vλ=2v⋅fccf_D = \frac{2v}{\lambda} = \frac{2v \cdot f_c}{c}fD=λ2v=c2v⋅fc
在脉冲多普勒雷达中,多普勒频移通过分析连续脉冲间的相位变化来测量。设第nnn个脉冲发射时目标距离为Rn=R0+v⋅n⋅PRIR_n = R_0 + v \cdot n \cdot \text{PRI}Rn=R0+v⋅n⋅PRI,则该脉冲回波的相位为:
ϕn=4πRnλ=4πR0λ+4πv⋅n⋅PRIλ\phi_n = \frac{4\pi R_n}{\lambda} = \frac{4\pi R_0}{\lambda} + \frac{4\pi v \cdot n \cdot \text{PRI}}{\lambda}ϕn=λ4πRn=λ4πR0+λ4πv⋅n⋅PRI
相邻脉冲间的相位差为:
Δϕ=ϕn+1−ϕn=4πv⋅PRIλ=2πfD⋅PRI\Delta \phi = \phi_{n+1} - \phi_n = \frac{4\pi v \cdot \text{PRI}}{\lambda} = 2\pi f_D \cdot \text{PRI}Δϕ=ϕn+1−ϕn=λ4πv⋅PRI=2πfD⋅PRI
这表明脉冲序列的相位以频率fDf_DfD线性增长。通过对nPRIn_{\text{PRI}}nPRI个脉冲的复数据进行FFT,可以提取出多普勒频率,进而计算速度:
v=fD⋅λ2=fD⋅c2fcv = \frac{f_D \cdot \lambda}{2} = \frac{f_D \cdot c}{2 f_c}v=2fD⋅λ=2fcfD⋅c
A.4 速度分辨率与最大不模糊速度
速度分辨率由相干积分时间决定。对于nPRIn_{\text{PRI}}nPRI个脉冲,总积分时间为tc=nPRI⋅PRIt_c = n_{\text{PRI}} \cdot \text{PRI}tc=nPRI⋅PRI,多普勒频率分辨率为:
ΔfD=1tc=1nPRI⋅PRI\Delta f_D = \frac{1}{t_c} = \frac{1}{n_{\text{PRI}} \cdot \text{PRI}}ΔfD=tc1=nPRI⋅PRI1
对应的速度分辨率:
Δv=ΔfD⋅λ2=λ2⋅nPRI⋅PRI=c2fc⋅nPRI⋅PRI\Delta v = \frac{\Delta f_D \cdot \lambda}{2} = \frac{\lambda}{2 \cdot n_{\text{PRI}} \cdot \text{PRI}} = \frac{c}{2 f_c \cdot n_{\text{PRI}} \cdot \text{PRI}}Δv=2ΔfD⋅λ=2⋅nPRI⋅PRIλ=2fc⋅nPRI⋅PRIc
代入本系统参数(fc=340f_c = 340fc=340 GHz, nPRI=128n_{\text{PRI}} = 128nPRI=128, PRI = 102.4 μs):
Δv=3×1082×340×109×128×102.4×10−6=0.034 m/s=3.4 cm/s\Delta v = \frac{3 \times 10^8}{2 \times 340 \times 10^9 \times 128 \times 102.4 \times 10^{-6}} = 0.034 \text{ m/s} = 3.4 \text{ cm/s}Δv=2×340×109×128×102.4×10−63×108=0.034 m/s=3.4 cm/s
(原文给出的3.8 cm/s略有不同,可能是由于汉宁窗展宽或参数取值的细微差异)
最大不模糊速度由采样定理决定。多普勒频率的采样率为fs=1/PRIf_s = 1/\text{PRI}fs=1/PRI,根据奈奎斯特定理,可无模糊测量的最大多普勒频率为:
fD,max=fs2=12⋅PRIf_{D,\max} = \frac{f_s}{2} = \frac{1}{2 \cdot \text{PRI}}fD,max=2fs=2⋅PRI1
对应的最大不模糊速度:
vmax=fD,max⋅λ2=λ4⋅PRI=c4fc⋅PRIv_{\max} = \frac{f_{D,\max} \cdot \lambda}{2} = \frac{\lambda}{4 \cdot \text{PRI}} = \frac{c}{4 f_c \cdot \text{PRI}}vmax=2fD,max⋅λ=4⋅PRIλ=4fc⋅PRIc
代入参数:
vmax=3×1084×340×109×102.4×10−6=2.15 m/sv_{\max} = \frac{3 \times 10^8}{4 \times 340 \times 10^9 \times 102.4 \times 10^{-6}} = 2.15 \text{ m/s}vmax=4×340×109×102.4×10−63×108=2.15 m/s
(注:原文给出4.3 m/s,这是双向最大值±2.15 m/s的全范围)
A.5 雷达方程与探测能力
雷达方程描述了接收功率与系统参数和目标特性的关系。对于单站雷达:
Pr=PtG2λ2σ(4π)3R4LP_r = \frac{P_t G^2 \lambda^2 \sigma}{(4\pi)^3 R^4 L}Pr=(4π)3R4LPtG2λ2σ
其中PtP_tPt是发射功率(约1 mW),GGG是天线增益,σ\sigmaσ是目标雷达截面积(RCS),RRR是目标距离,LLL是系统损耗因子。
对于准直波束系统,天线增益与孔径面积AantA_{\text{ant}}Aant相关:
G=4πAantλ2⋅ηG = \frac{4\pi A_{\text{ant}}}{\lambda^2} \cdot \etaG=λ24πAant⋅η
其中η\etaη是天线效率。
A.6 小粒子的雷达截面积
对于半径aaa远小于波长λ\lambdaλ的球形粒子,散射处于瑞利区域。瑞利散射的RCS为:
σRayleigh=128π5a63λ4∣εr−1εr+2∣2\sigma_{\text{Rayleigh}} = \frac{128 \pi^5 a^6}{3 \lambda^4} \left| \frac{\varepsilon_r - 1}{\varepsilon_r + 2} \right|^2σRayleigh=3λ4128π5a6 εr+2εr−1 2
其中εr\varepsilon_rεr是粒子材料的相对介电常数。关键特征是RCS与粒子半径的6次方成正比,与波长的4次方成反比:
σ∝a6λ4\sigma \propto \frac{a^6}{\lambda^4}σ∝λ4a6
这解释了为什么亚毫米波(短波长)更适合检测小粒子:同样大小的粒子,在340 GHz(λ≈0.88\lambda \approx 0.88λ≈0.88 mm)的RCS比在34 GHz(λ≈8.8\lambda \approx 8.8λ≈8.8 mm)高约10410^4104倍。
对于金属球(理想导体,∣εr∣→∞|\varepsilon_r| \to \infty∣εr∣→∞),上式简化为:
σmetal=128π5a63λ4\sigma_{\text{metal}} = \frac{128 \pi^5 a^6}{3 \lambda^4}σmetal=3λ4128π5a6
对于直径100 μm(a=50a = 50a=50 μm)的金属粒子在340 GHz:
σ=128π5(50×10−6)63(0.88×10−3)4≈2.7×10−15 m2=−145.7 dBsm\sigma = \frac{128 \pi^5 (50 \times 10^{-6})^6}{3 (0.88 \times 10^{-3})^4} \approx 2.7 \times 10^{-15} \text{ m}^2 = -145.7 \text{ dBsm}σ=3(0.88×10−3)4128π5(50×10−6)6≈2.7×10−15 m2=−145.7 dBsm
这是一个极小的RCS,但由于相干积分增益和低噪声系统设计,仍可实现可靠检测。
A.7 相干积分增益
脉冲多普勒雷达的一个重要优势是相干积分可以提高信噪比。对于nPRIn_{\text{PRI}}nPRI个相干脉冲,在目标和系统保持相干的条件下:
信号功率随脉冲数平方增长(因为复数信号相干相加):
Ps,total=nPRI2⋅Ps,singleP_{s,\text{total}} = n_{\text{PRI}}^2 \cdot P_{s,\text{single}}Ps,total=nPRI2⋅Ps,single
噪声功率随脉冲数线性增长(因为噪声是不相关的):
Pn,total=nPRI⋅Pn,singleP_{n,\text{total}} = n_{\text{PRI}} \cdot P_{n,\text{single}}Pn,total=nPRI⋅Pn,single
因此,相干积分增益为:
Gcoherent=(Ps/Pn)total(Ps/Pn)single=nPRIG_{\text{coherent}} = \frac{(P_s/P_n){\text{total}}}{(P_s/P_n){\text{single}}} = n_{\text{PRI}}Gcoherent=(Ps/Pn)single(Ps/Pn)total=nPRI
以分贝表示:
Gcoherent[dB]=10log10(nPRI)G_{\text{coherent}}[\text{dB}] = 10 \log_{10}(n_{\text{PRI}})Gcoherent[dB]=10log10(nPRI)
对于nPRI=128n_{\text{PRI}} = 128nPRI=128,相干积分增益约为21 dB。图6的实验结果验证了这一线性关系:脉冲数每翻倍,信噪比提高约3 dB。
A.8 自由落体模型完整推导
考虑一个质量为mmm、横截面积为AAA的球体在空气中下落。作用在球体上的力包括重力mgmgmg(向下)和空气阻力FdF_dFd(向上)。空气阻力与速度平方成正比:
Fd=12ρairv2cdAF_d = \frac{1}{2} \rho_{\text{air}} v^2 c_d AFd=21ρairv2cdA
其中ρair\rho_{\text{air}}ρair是空气密度,cdc_dcd是阻力系数(球体约0.47),vvv是下落速度。
牛顿第二定律给出:
mdvdt=mg−12ρairv2cdAm \frac{dv}{dt} = mg - \frac{1}{2} \rho_{\text{air}} v^2 c_d Amdtdv=mg−21ρairv2cdA
定义终端速度vtv_tvt为阻力等于重力时的速度:
mg=12ρairvt2cdAmg = \frac{1}{2} \rho_{\text{air}} v_t^2 c_d Amg=21ρairvt2cdA
vt=2mgρaircdAv_t = \sqrt{\frac{2mg}{\rho_{\text{air}} c_d A}}vt=ρaircdA2mg
定义特征时间τ=vt/g\tau = v_t / gτ=vt/g,运动方程变为:
dvdt=g(1−v2vt2)\frac{dv}{dt} = g\left(1 - \frac{v^2}{v_t^2}\right)dtdv=g(1−vt2v2)
这是一个可分离变量的一阶常微分方程。令u=v/vtu = v/v_tu=v/vt:
vtdudt=g(1−u2)v_t \frac{du}{dt} = g(1 - u^2)vtdtdu=g(1−u2)
du1−u2=gvtdt=dtτ\frac{du}{1 - u^2} = \frac{g}{v_t} dt = \frac{dt}{\tau}1−u2du=vtgdt=τdt
对左边使用部分分式分解:
11−u2=12(11+u+11−u)\frac{1}{1-u^2} = \frac{1}{2}\left(\frac{1}{1+u} + \frac{1}{1-u}\right)1−u21=21(1+u1+1−u1)
积分得:
12ln(1+u1−u)=tτ+C\frac{1}{2}\ln\left(\frac{1+u}{1-u}\right) = \frac{t}{\tau} + C21ln(1−u1+u)=τt+C
应用初始条件v(0)=0v(0) = 0v(0)=0,即u(0)=0u(0) = 0u(0)=0,得C=0C = 0C=0。因此:
1+u1−u=e2t/τ\frac{1+u}{1-u} = e^{2t/\tau}1−u1+u=e2t/τ
解出uuu:
u=e2t/τ−1e2t/τ+1=et/τ−e−t/τet/τ+e−t/τ=tanh(t/τ)u = \frac{e^{2t/\tau} - 1}{e^{2t/\tau} + 1} = \frac{e^{t/\tau} - e^{-t/\tau}}{e^{t/\tau} + e^{-t/\tau}} = \tanh(t/\tau)u=e2t/τ+1e2t/τ−1=et/τ+e−t/τet/τ−e−t/τ=tanh(t/τ)
因此速度为:
v(t)=vttanh(t/τ)(1a)v(t) = v_t \tanh(t/\tau) \tag{1a}v(t)=vttanh(t/τ)(1a)
位置由速度积分得到。设初始位置为x0x_0x0(下落方向为负):
x(t)=x0−∫0tv(t′)dt′=x0−vt∫0ttanh(t′/τ)dt′x(t) = x_0 - \int_0^t v(t') dt' = x_0 - v_t \int_0^t \tanh(t'/\tau) dt'x(t)=x0−∫0tv(t′)dt′=x0−vt∫0ttanh(t′/τ)dt′
利用积分公式∫tanh(x)dx=ln(cosh(x))\int \tanh(x) dx = \ln(\cosh(x))∫tanh(x)dx=ln(cosh(x)):
x(t)=x0−vtτ[ln(cosh(t′/τ))]0t=x0−vtτln(cosh(t/τ))(1b)x(t) = x_0 - v_t \tau \left[\ln(\cosh(t'/\tau))\right]_0^t = x_0 - v_t \tau \ln(\cosh(t/\tau)) \tag{1b}x(t)=x0−vtτ[ln(cosh(t′/τ))]0t=x0−vtτln(cosh(t/τ))(1b)
对于本实验中的10 mm直径、4 g质量的金属球,设ρair=1.2\rho_{\text{air}} = 1.2ρair=1.2 kg/m³,cd=0.47c_d = 0.47cd=0.47,A=π(5×10−3)2=7.85×10−5A = \pi (5 \times 10^{-3})^2 = 7.85 \times 10^{-5}A=π(5×10−3)2=7.85×10−5 m²:
vt=2×0.004×9.81.2×0.47×7.85×10−5≈13.3 m/sv_t = \sqrt{\frac{2 \times 0.004 \times 9.8}{1.2 \times 0.47 \times 7.85 \times 10^{-5}}} \approx 13.3 \text{ m/s}vt=1.2×0.47×7.85×10−52×0.004×9.8 ≈13.3 m/s
τ=13.39.8≈1.36 s\tau = \frac{13.3}{9.8} \approx 1.36 \text{ s}τ=9.813.3≈1.36 s
在实验观测的时间尺度内(约1秒),球体速度远未达到终端速度,因此tanh(t/τ)\tanh(t/\tau)tanh(t/τ)近似为线性,即v≈gtv \approx gtv≈gt(自由落体近似)。但随着速度增加,空气阻力效应变得明显,轨迹开始偏离简单的抛物线。图8©中理论曲线与实验数据的良好吻合验证了这一完整模型的正确性。