【机器学习】深度信念网络（DBN）

深度信念网络（Deep Belief Network, DBN）是由 Geoffrey Hinton 于 2006 年提出的一种生成式深度学习模型，是深度学习领域的里程碑式模型之一。它通过堆叠多个限制玻尔兹曼机（Restricted Boltzmann Machine, RBM）构建深层结构，结合了无监督预训练和有监督微调的训练策略，有效解决了传统深度神经网络训练中 "梯度消失" 的问题，为后续深度学习的爆发奠定了基础。

二、核心定义与本质

DBN 是一种概率生成模型（区别于 CNN、Transformer 等判别式模型），其核心本质是：

通过多层隐藏单元学习数据的概率分布，而非直接学习输入到输出的映射；
能够从数据中自动提取多层级的抽象特征（从底层像素 / 原始特征到高层语义特征）；
结构上由 "堆叠的 RBM + 顶层逻辑回归 /softmax 层" 组成，兼具生成能力（重构输入）和判别能力（分类 / 回归）。

三、网络结构详解

DBN 的结构呈 "堆叠式"，自上而下分为三部分：输入层（可见层）→ 隐藏层（多层 RBM 堆叠）→ 输出层（分类 / 回归头），核心组件是限制玻尔兹曼机（RBM）。

1. 基础组件：限制玻尔兹曼机（RBM）

RBM 是一种二分图结构的无向概率图模型，是 DBN 的核心积木，结构如下：

可见层（Visible Layer, v）：接收输入数据（如图像像素、特征向量），节点数 = 输入维度；
隐藏层（Hidden Layer, h）：学习输入数据的抽象特征，节点数为超参数；
核心限制：层内无连接（可见层节点间无连接，隐藏层节点间无连接），仅层间全连接（每个可见节点与所有隐藏节点相连）。

RBM 的核心数学原理

RBM 通过能量函数定义模型的概率分布：

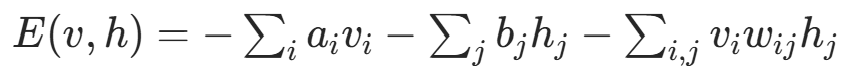
其中：

：可见层第 i 个节点的偏置；
：隐藏层第 j 个节点的偏置；
：可见层 i 与隐藏层 j 之间的连接权重；
：可见层 / 隐藏层节点的状态（二进制节点取值 {0,1}，高斯节点取值为连续值）。

基于能量函数，可见层与隐藏层的联合概率分布为：

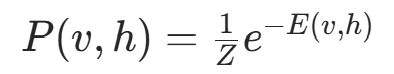
其中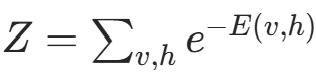是配分函数（归一化因子）。

RBM 的条件概率

由于 RBM 层内无连接，给定可见层状态 v 时，隐藏层节点的激活状态相互独立；反之亦然：

其中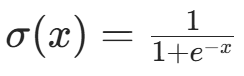是 sigmoid 函数（适用于二进制数据）；若为连续数据（如归一化后的图像），可见层可采用高斯分布。

2. DBN 的整体结构

DBN 由 L 个 RBM 堆叠而成，上层 RBM 的隐藏层作为下层 RBM 的可见层，最后添加一个输出层（用于分类 / 回归）：

第 1 层 RBM：可见层 = DBN 输入层（原始数据），隐藏层 = 第 1 层抽象特征；
第 2 层 RBM：可见层 = 第 1 层 RBM 的隐藏层，隐藏层 = 第 2 层抽象特征；
...
第 L 层 RBM：可见层 = 第 L-1 层 RBM 的隐藏层，隐藏层 = 最高层抽象特征；
输出层：接收最高层隐藏特征，通过逻辑回归（二分类）或 softmax（多分类）输出预测结果。

示意图：

bash 复制代码

输入数据（v1） → RBM1 隐藏层（h1） → RBM2 隐藏层（h2） → ... → RBMk 隐藏层（hk） → 输出层（预测结果）

四、核心训练流程

DBN 的训练分为两大步：无监督贪心逐层预训练 + 有监督微调，这是其解决梯度消失问题的关键。

1. 第一步：无监督贪心逐层预训练

目标：通过无监督学习，让每一层 RBM 学习数据的底层特征，为深层网络初始化合理的权重（避免随机初始化导致的梯度消失）。

"贪心"：每次只训练一层 RBM，固定已训练层的权重，仅更新当前层的权重和偏置；
"逐层"：从下到上训练（先训练第 1 层 RBM，再训练第 2 层 RBM，直到所有 RBM 训练完成）；
训练算法：对比散度（Contrastive Divergence, CD-k）------ 替代传统的马尔可夫链蒙特卡洛（MCMC）采样，大幅提升训练速度。

CD-k 训练 RBM 的步骤（以 k=1 为例）：

正向采样 ：给定输入数据，计算隐藏层状态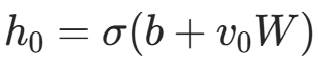（采样或直接用概率作为状态）；
反向重构 ：用重构可见层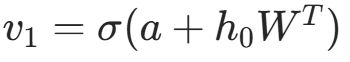（二进制数据采样，连续数据直接输出）；
负向采样 ：用重构的计算隐藏层状态；
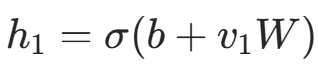权重更新：通过最小化重构误差（或最大化对数似然）更新权重和偏置：

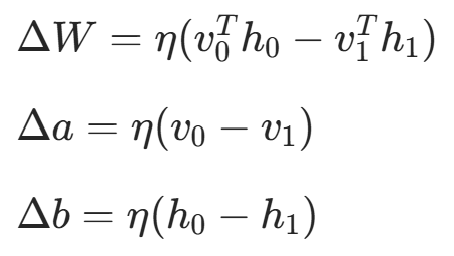
其中 η 是学习率。

2. 第二步：有监督微调

目标：在预训练的基础上，通过有监督学习调整整个网络的权重（包括所有 RBM 层和输出层），提升模型的判别性能。

将顶层 RBM 的隐藏层与输出层连接（如 softmax 层）；
定义有监督损失函数（如分类任务的交叉熵损失）；
采用反向传播（BP）算法或共轭梯度下降，对整个网络的权重进行微调（从输出层到输入层反向传播梯度）。

为什么需要微调？

预训练仅让每一层 RBM 学习到数据的通用特征，但未考虑具体任务（如分类）的需求。微调通过任务相关的损失函数，调整权重以适配特定任务，大幅提升模型性能。

五、DBN 的核心特性

1. 优点

解决梯度消失：贪心预训练为深层网络提供了接近最优解的初始权重，反向微调时梯度不易消失；
自动特征提取：无需人工设计特征（如 SVM 需手动提取 HOG、SIFT 特征），模型自动学习多层级抽象特征；
兼具生成与判别能力：可用于生成式任务（如重构图像、生成新样本）和判别式任务（如分类、回归）；
适用于小样本数据：预训练利用无标签数据（半监督学习），在标签数据有限时仍能保持较好性能。

2. 缺点

训练复杂：需分两步训练（预训练 + 微调），超参数调优（RBM 层数、隐藏节点数、学习率等）繁琐；
训练速度慢：CD-k 采样仍需迭代，且深层网络微调耗时；
性能受限：生成能力弱于后续的 GAN、VAE，判别能力弱于 CNN、Transformer，目前在主流任务中已被替代；
仅适用于简单结构数据：对图像、语音等网格 / 序列数据的适配性不如 CNN、RNN。

六、典型应用场景

尽管 DBN 已不是主流模型，但在特定场景仍有应用，且其核心思想（预训练、深层特征学习）影响深远：

特征学习与降维：对高维数据（如文本、基因数据）进行特征提取和降维，用于后续分类任务；
图像识别：早期用于 MNIST、CIFAR-10 等简单图像分类，现在已被 CNN 替代；
推荐系统：学习用户 - 物品交互的隐向量表示，用于协同过滤推荐；
语音识别：提取语音信号的深层特征，辅助声学模型训练；
异常检测：通过学习正常数据的概率分布，识别偏离分布的异常样本（如欺诈检测、故障诊断）；
半监督学习：在标签数据稀缺时，利用大量无标签数据预训练，提升模型泛化能力。

七、基于深度信念网络（DBN）的Python代码完整实现

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
import numpy as np
import pandas as pd  # 新增导入
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm
from sklearn.metrics import confusion_matrix
import warnings

warnings.filterwarnings('ignore')  # 忽略绘图警告

# 设置绘图风格
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")
plt.rcParams['figure.figsize'] = (12, 8)


# -------------------------- 1. 通用合成分类数据集 --------------------------
class SyntheticClassificationDataset(Dataset):
    """通用合成分类数据集：一维特征向量 + 分类标签"""

    def __init__(self, num_samples=10000, feature_dim=32, num_classes=10, train=True):
        self.num_samples = num_samples
        self.feature_dim = feature_dim
        self.num_classes = num_classes

        # 生成随机特征（正态分布）
        self.features = torch.randn(num_samples, feature_dim)
        # 生成随机分类标签
        self.labels = torch.randint(0, num_classes, (num_samples,))

        # 划分训练/测试集
        split_idx = int(num_samples * 0.8)
        if train:
            self.features = self.features[:split_idx]
            self.labels = self.labels[:split_idx]
        else:
            self.features = self.features[split_idx:]
            self.labels = self.labels[split_idx:]

    def __len__(self):
        return len(self.features)

    def __getitem__(self, idx):
        return self.features[idx], self.labels[idx]


# -------------------------- 2. 定义 RBM 类 --------------------------
class RBM(nn.Module):
    def __init__(self, visible_dim, hidden_dim, device='cuda'):
        super(RBM, self).__init__()
        self.visible_dim = visible_dim
        self.hidden_dim = hidden_dim
        self.device = device

        # 权重和偏置初始化
        self.W = nn.Parameter(torch.randn(visible_dim, hidden_dim) * 0.01)
        self.a = nn.Parameter(torch.zeros(visible_dim))
        self.b = nn.Parameter(torch.zeros(hidden_dim))

    def forward(self, v):
        """正向传播：计算隐藏层概率"""
        h_prob = torch.sigmoid(torch.matmul(v, self.W) + self.b)
        return h_prob

    def sample_h(self, v):
        """采样隐藏层"""
        h_prob = self.forward(v)
        h_sample = torch.bernoulli(h_prob)
        return h_prob, h_sample

    def sample_v(self, h):
        """采样可见层"""
        v_prob = torch.sigmoid(torch.matmul(h, self.W.t()) + self.a)
        v_sample = torch.bernoulli(v_prob)
        return v_prob, v_sample

    def contrastive_divergence(self, v0, k=1):
        """CD-k 算法，返回重构误差和梯度"""
        h0_prob, h0_sample = self.sample_h(v0)
        vk_prob, vk_sample = self.sample_v(h0_sample)
        hk_prob, hk_sample = self.sample_h(vk_sample)

        # 计算梯度
        grad_W = torch.matmul(v0.t(), h0_prob) - torch.matmul(vk_sample.t(), hk_prob)
        grad_a = torch.sum(v0 - vk_sample, dim=0)
        grad_b = torch.sum(h0_prob - hk_prob, dim=0)

        # 重构误差
        reconstruction_error = torch.mean((v0 - vk_prob) ** 2)
        return reconstruction_error, grad_W, grad_a, grad_b


# -------------------------- 3. 定义 DBN 类（含指标记录） --------------------------
class DBN(nn.Module):
    def __init__(self, input_dim, hidden_dims, output_dim, device='cuda'):
        super(DBN, self).__init__()
        self.input_dim = input_dim
        self.hidden_dims = hidden_dims
        self.output_dim = output_dim
        self.device = device
        self.num_rbms = len(hidden_dims)

        # 堆叠 RBM 层
        self.rbms = nn.ModuleList()
        prev_dim = input_dim
        for hidden_dim in hidden_dims:
            self.rbms.append(RBM(prev_dim, hidden_dim, device))
            prev_dim = hidden_dim

        # 输出层
        self.output_layer = nn.Sequential(
            nn.Linear(prev_dim, output_dim),
            nn.Softmax(dim=1)
        )

        # 记录训练指标（用于可视化）
        self.rbm_recon_errors = {}  # 每层RBM的重构误差: {rbm_idx: [error1, error2,...]}
        self.finetune_train_loss = []
        self.finetune_test_loss = []
        self.finetune_train_acc = []
        self.finetune_test_acc = []
        # 记录隐藏层激活值
        self.hidden_activations = {}

    def pretrain(self, dataloader, lr=0.01, epochs=5, k=1):
        """无监督预训练 + 记录重构误差"""
        for rbm_idx in range(self.num_rbms):
            print(f"\n===== 预训练第 {rbm_idx + 1}/{self.num_rbms} 层 RBM =====")
            current_rbm = self.rbms[rbm_idx]
            optimizer = optim.SGD([current_rbm.W, current_rbm.a, current_rbm.b], lr=lr)
            self.rbm_recon_errors[rbm_idx] = []  # 初始化误差列表

            # 带进度条的训练循环
            for epoch in tqdm(range(epochs), desc=f"RBM {rbm_idx + 1} 训练"):
                total_error = 0.0
                for batch_idx, (data, _) in enumerate(dataloader):
                    # 数据预处理
                    v0 = data.to(self.device)
                    v0 = (v0 > 0).float()

                    # 多层RBM输入处理
                    if rbm_idx > 0:
                        prev_v = v0
                        for prev_rbm_idx in range(rbm_idx):
                            _, prev_v = self.rbms[prev_rbm_idx].sample_h(prev_v)
                        v0 = prev_v

                    # CD-k 训练
                    recon_error, grad_W, grad_a, grad_b = current_rbm.contrastive_divergence(v0, k)
                    optimizer.zero_grad()
                    current_rbm.W.grad = -grad_W / data.size(0)
                    current_rbm.a.grad = -grad_a / data.size(0)
                    current_rbm.b.grad = -grad_b / data.size(0)
                    optimizer.step()

                    total_error += recon_error.item() * data.size(0)

                # 记录每轮平均误差
                avg_error = total_error / len(dataloader.dataset)
                self.rbm_recon_errors[rbm_idx].append(avg_error)
                tqdm.write(f"RBM {rbm_idx + 1} Epoch {epoch + 1}, Reconstruction Error: {avg_error:.4f}")

    def forward(self, x):
        """正向传播 + 记录隐藏层激活值"""
        x = x.to(self.device)
        activations = []
        for rbm in self.rbms:
            x = rbm(x)
            activations.append(x.detach().cpu().numpy())
        # 保存最后一次前向传播的激活值（用于可视化）
        self.hidden_activations = {i: act for i, act in enumerate(activations)}
        output = self.output_layer(x)
        return output

    def finetune(self, train_loader, test_loader, lr=0.001, epochs=8):
        """有监督微调 + 记录损失/准确率"""
        criterion = nn.CrossEntropyLoss()
        all_params = list(self.rbms.parameters()) + list(self.output_layer.parameters())
        optimizer = optim.Adam(all_params, lr=lr)

        print("\n===== 开始微调 DBN =====")
        for epoch in tqdm(range(epochs), desc="微调训练"):
            # 训练阶段
            self.train()
            train_loss = 0.0
            correct = 0
            total = 0
            for data, targets in train_loader:
                data, targets = data.to(self.device), targets.to(self.device)
                optimizer.zero_grad()
                outputs = self.forward(data)
                loss = criterion(outputs, targets)
                loss.backward()
                optimizer.step()

                train_loss += loss.item() * data.size(0)
                _, predicted = torch.max(outputs, 1)
                total += targets.size(0)
                correct += (predicted == targets).sum().item()

            # 计算训练指标
            avg_train_loss = train_loss / total
            train_acc = correct / total
            self.finetune_train_loss.append(avg_train_loss)
            self.finetune_train_acc.append(train_acc)

            # 测试阶段
            self.eval()
            test_loss = 0.0
            correct = 0
            total = 0
            all_preds = []
            all_targets = []
            with torch.no_grad():
                for data, targets in test_loader:
                    data, targets = data.to(self.device), targets.to(self.device)
                    outputs = self.forward(data)
                    loss = criterion(outputs, targets)

                    test_loss += loss.item() * data.size(0)
                    _, predicted = torch.max(outputs, 1)
                    total += targets.size(0)
                    correct += (predicted == targets).sum().item()

                    # 保存预测结果（用于混淆矩阵）
                    all_preds.extend(predicted.cpu().numpy())
                    all_targets.extend(targets.cpu().numpy())

            # 计算测试指标
            avg_test_loss = test_loss / total
            test_acc = correct / total
            self.finetune_test_loss.append(avg_test_loss)
            self.finetune_test_acc.append(test_acc)

            # 记录并打印
            tqdm.write(
                f"Epoch {epoch + 1} | Train Loss: {avg_train_loss:.4f} | Train Acc: {train_acc:.4f} | "
                f"Test Loss: {avg_test_loss:.4f} | Test Acc: {test_acc:.4f}"
            )
        # 保存混淆矩阵数据
        self.confusion_matrix = confusion_matrix(all_targets, all_preds)
        self.classes = list(range(self.output_dim))
        # 保存输入特征数据（用于分布可视化）
        self.input_features = next(iter(train_loader))[0].cpu().numpy()


# -------------------------- 4. 可视化函数 --------------------------
def plot_rbm_recon_errors(dbn):
    """绘制每层RBM的重构误差曲线"""
    plt.figure(figsize=(10, 6))
    for rbm_idx, errors in dbn.rbm_recon_errors.items():
        epochs = range(1, len(errors) + 1)
        plt.plot(epochs, errors, marker='o', linewidth=2, label=f'RBM {rbm_idx + 1}')

    plt.title('RBM Pre-Training: Reconstruction Error vs Epoch', fontsize=14)
    plt.xlabel('Epoch', fontsize=12)
    plt.ylabel('Reconstruction Error (MSE)', fontsize=12)
    plt.legend(fontsize=10)
    plt.grid(True, alpha=0.3)
    plt.savefig('rbm_recon_errors.png', dpi=300, bbox_inches='tight')
    plt.show()


def plot_finetune_metrics(dbn):
    """绘制微调阶段的损失和准确率曲线"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

    # 损失曲线
    epochs = range(1, len(dbn.finetune_train_loss) + 1)
    ax1.plot(epochs, dbn.finetune_train_loss, marker='o', linewidth=2, label='Train Loss')
    ax1.plot(epochs, dbn.finetune_test_loss, marker='s', linewidth=2, label='Test Loss')
    ax1.set_title('Finetune: Loss vs Epoch', fontsize=14)
    ax1.set_xlabel('Epoch', fontsize=12)
    ax1.set_ylabel('Cross-Entropy Loss', fontsize=12)
    ax1.legend(fontsize=10)
    ax1.grid(True, alpha=0.3)

    # 准确率曲线
    ax2.plot(epochs, dbn.finetune_train_acc, marker='o', linewidth=2, label='Train Acc')
    ax2.plot(epochs, dbn.finetune_test_acc, marker='s', linewidth=2, label='Test Acc')
    ax2.set_title('Finetune: Accuracy vs Epoch', fontsize=14)
    ax2.set_xlabel('Epoch', fontsize=12)
    ax2.set_ylabel('Accuracy', fontsize=12)
    ax2.legend(fontsize=10)
    ax2.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('finetune_metrics.png', dpi=300, bbox_inches='tight')
    plt.show()


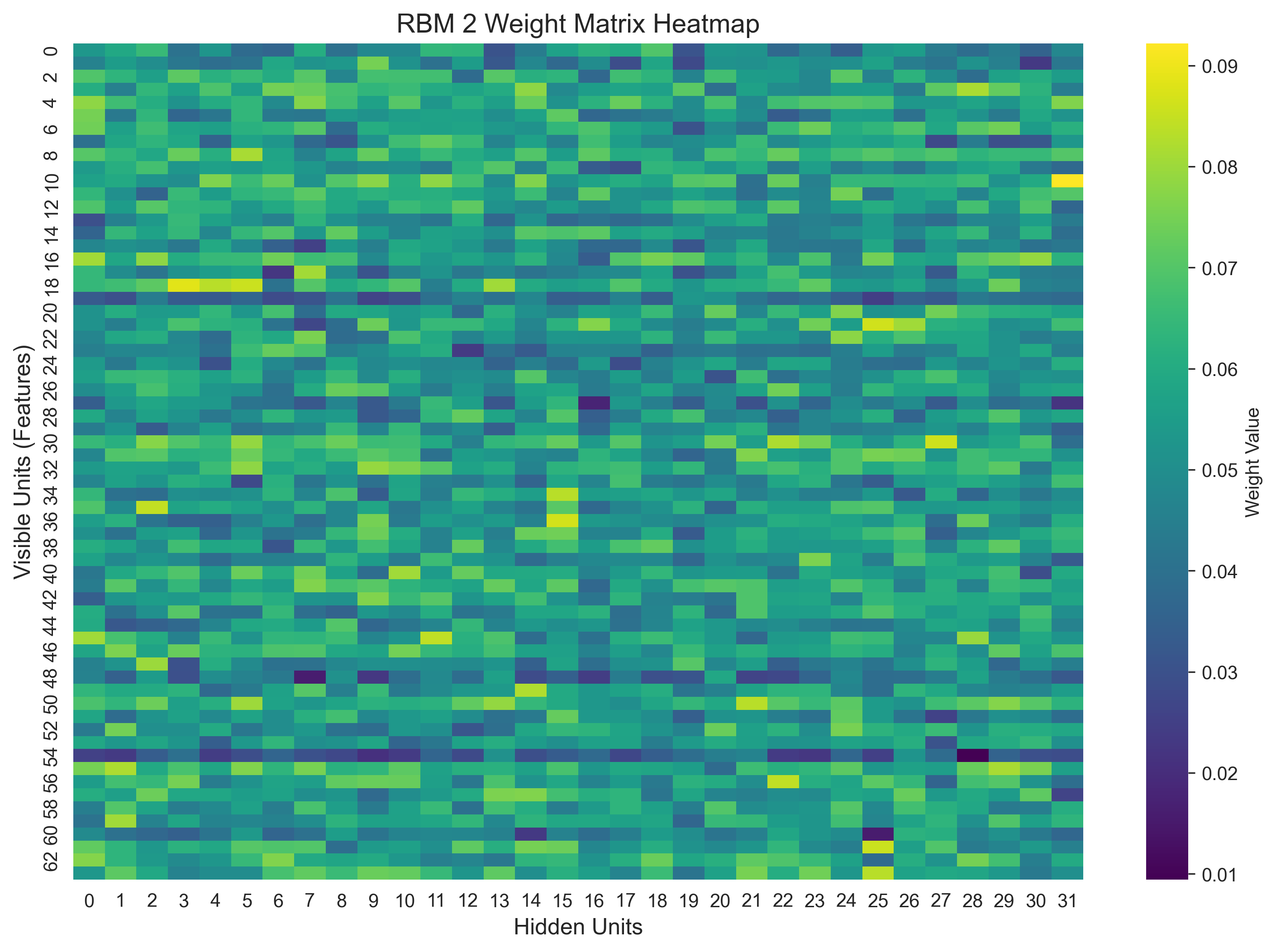
def plot_rbm_weights(dbn, rbm_idx=0):
    """绘制指定RBM的权重矩阵热力图"""
    if rbm_idx >= len(dbn.rbms):
        print(f"RBM索引超出范围（共{len(dbn.rbms)}层）")
        return

    rbm = dbn.rbms[rbm_idx]
    weights = rbm.W.detach().cpu().numpy()

    plt.figure(figsize=(12, 8))
    ax = sns.heatmap(
        weights,
        cmap='viridis',
        cbar_kws={'label': 'Weight Value'}
    )
    ax.set_aspect('auto')  # 正确设置热力图比例
    plt.title(f'RBM {rbm_idx + 1} Weight Matrix Heatmap', fontsize=14)
    plt.xlabel('Hidden Units', fontsize=12)
    plt.ylabel('Visible Units (Features)', fontsize=12)
    plt.savefig(f'rbm_{rbm_idx + 1}_weights.png', dpi=300, bbox_inches='tight')
    plt.show()


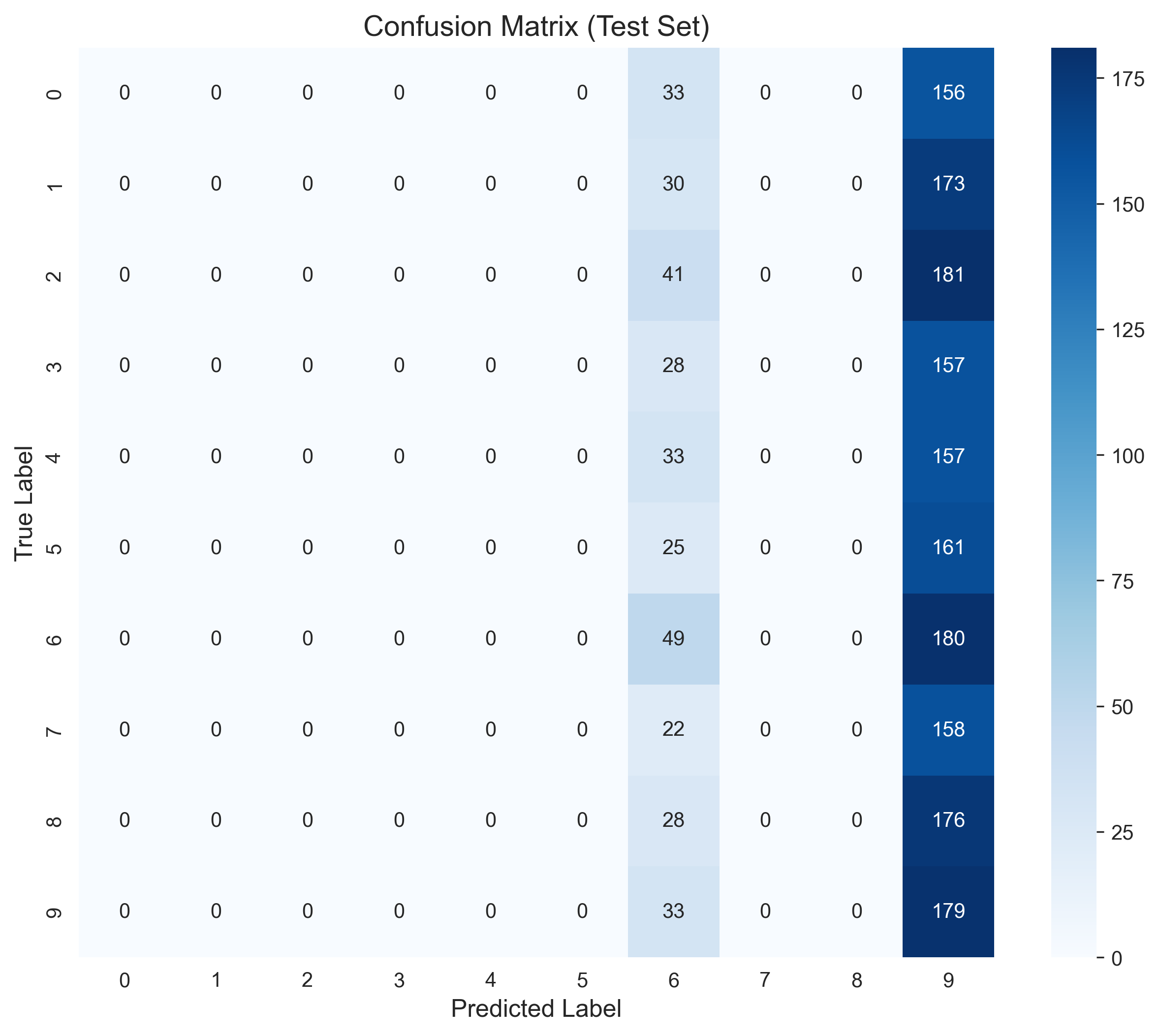
def plot_confusion_matrix(dbn):
    """绘制混淆矩阵"""
    plt.figure(figsize=(10, 8))
    sns.heatmap(
        dbn.confusion_matrix,
        annot=True,
        fmt='d',
        cmap='Blues',
        xticklabels=dbn.classes,
        yticklabels=dbn.classes
    )
    plt.title('Confusion Matrix (Test Set)', fontsize=14)
    plt.xlabel('Predicted Label', fontsize=12)
    plt.ylabel('True Label', fontsize=12)
    plt.savefig('confusion_matrix.png', dpi=300, bbox_inches='tight')
    plt.show()


# -------------------------- 新增可视化函数 --------------------------
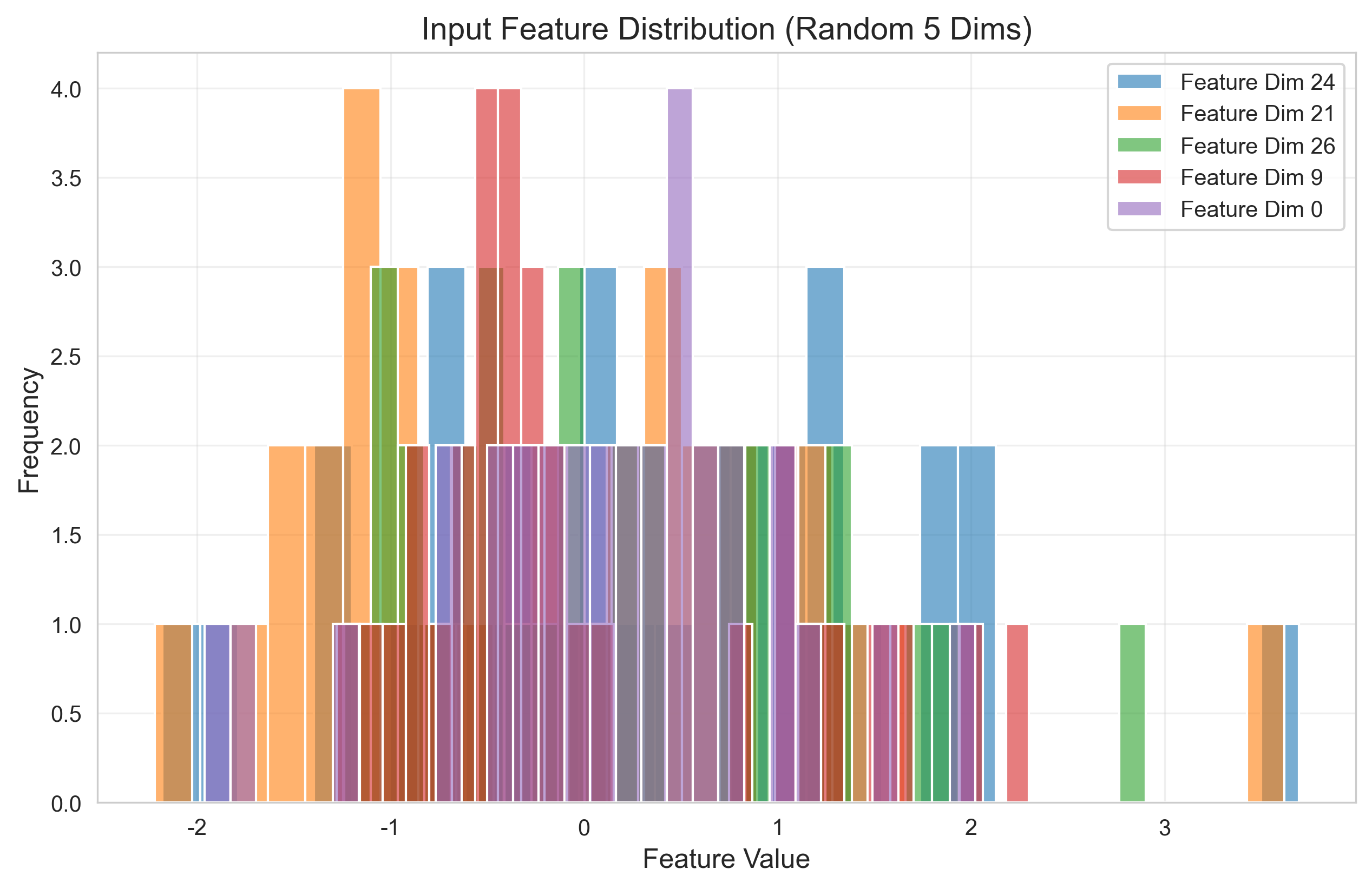
def plot_feature_distribution(dbn):
    """绘制输入特征的分布直方图"""
    features = dbn.input_features
    plt.figure(figsize=(10, 6))
    # 随机选5个特征维度绘制分布
    selected_dims = np.random.choice(features.shape[1], 5, replace=False)
    for dim in selected_dims:
        sns.histplot(features[:, dim], alpha=0.6, label=f'Feature Dim {dim}', bins=30)

    plt.title('Input Feature Distribution (Random 5 Dims)', fontsize=14)
    plt.xlabel('Feature Value', fontsize=12)
    plt.ylabel('Frequency', fontsize=12)
    plt.legend(fontsize=10)
    plt.grid(True, alpha=0.3)
    plt.savefig('feature_distribution.png', dpi=300, bbox_inches='tight')
    plt.show()


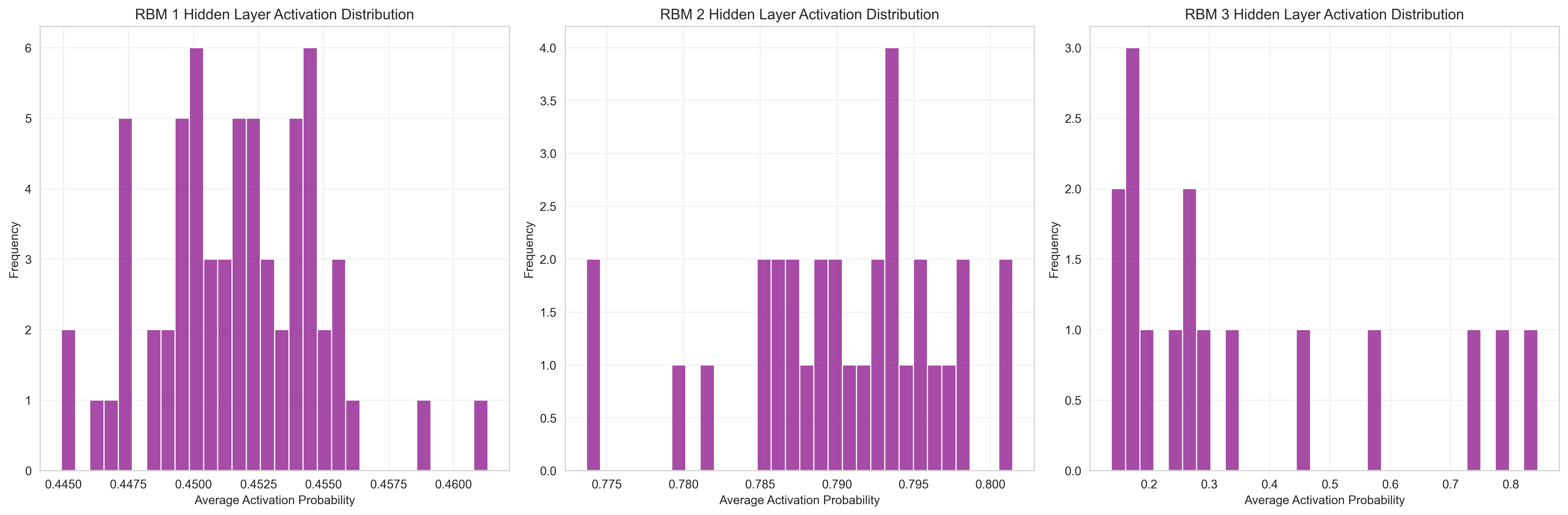
def plot_hidden_activation_dist(dbn):
    """绘制RBM隐藏层激活值分布"""
    if not dbn.hidden_activations:
        print("无隐藏层激活值数据，请先执行前向传播！")
        return

    fig, axes = plt.subplots(1, len(dbn.hidden_activations), figsize=(18, 6))
    if len(dbn.hidden_activations) == 1:
        axes = [axes]

    for idx, (rbm_idx, activations) in enumerate(dbn.hidden_activations.items()):
        # 计算每个隐藏单元的平均激活值
        avg_activations = np.mean(activations, axis=0)
        sns.histplot(avg_activations, ax=axes[idx], bins=30, color='purple', alpha=0.7)
        axes[idx].set_title(f'RBM {rbm_idx + 1} Hidden Layer Activation Distribution', fontsize=12)
        axes[idx].set_xlabel('Average Activation Probability', fontsize=10)
        axes[idx].set_ylabel('Frequency', fontsize=10)
        axes[idx].grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('hidden_activation_dist.png', dpi=300, bbox_inches='tight')
    plt.show()


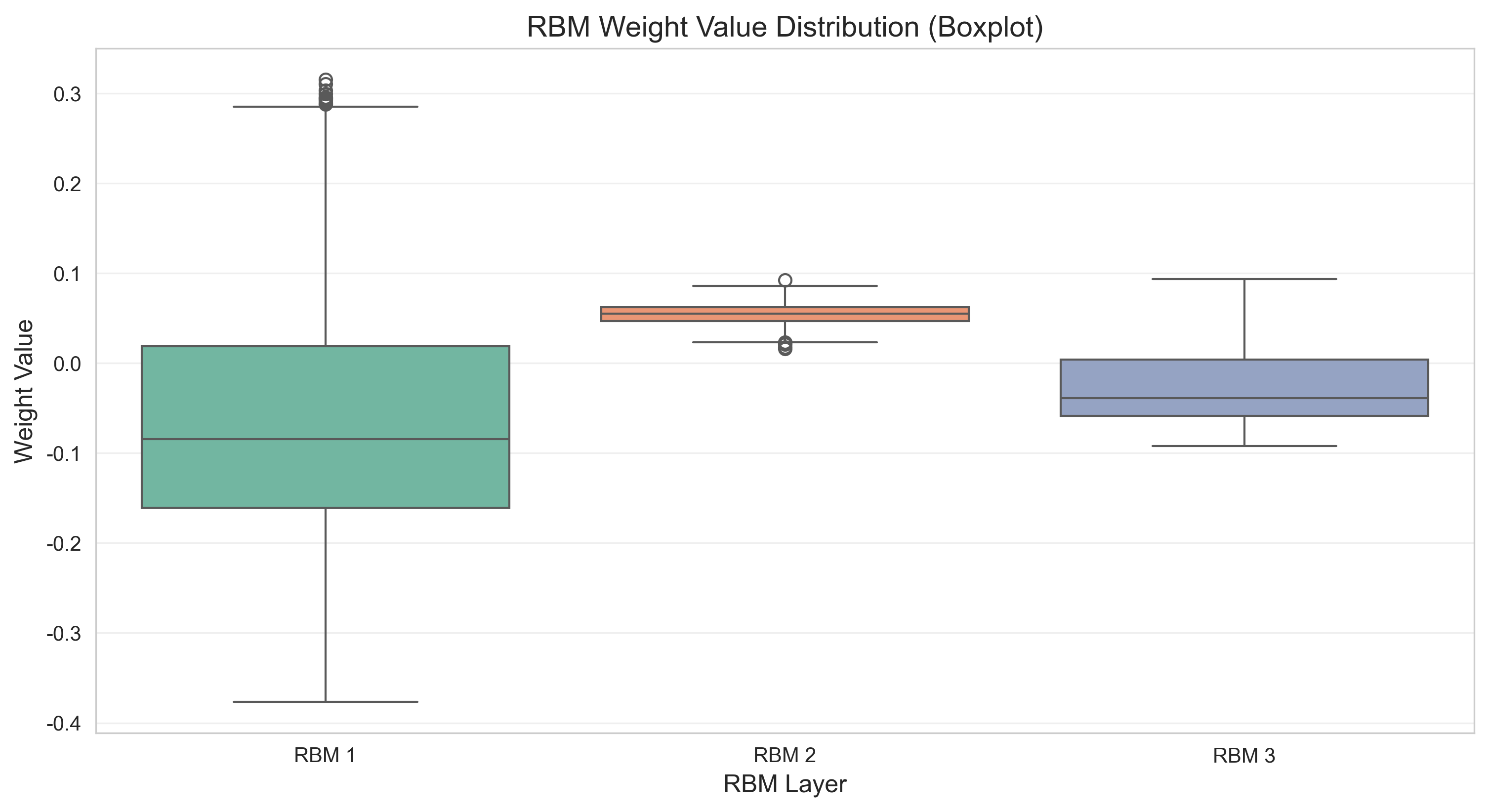
def plot_weight_distribution(dbn):
    """绘制各层RBM权重值的箱线图"""
    # 重构数据为DataFrame格式（适配seaborn）
    weight_list = []
    layer_list = []
    for rbm_idx, rbm in enumerate(dbn.rbms):
        weights = rbm.W.detach().cpu().numpy().flatten()
        # 随机采样1000个权重值（避免数据量过大）
        sample_weights = np.random.choice(weights, min(1000, len(weights)), replace=False)
        weight_list.extend(sample_weights)
        layer_list.extend([f'RBM {rbm_idx + 1}'] * len(sample_weights))

    # 转为DataFrame
    weight_df = pd.DataFrame({
        'Weight Value': weight_list,
        'RBM Layer': layer_list
    })

    plt.figure(figsize=(12, 6))
    sns.boxplot(x='RBM Layer', y='Weight Value', data=weight_df, palette='Set2')
    plt.title('RBM Weight Value Distribution (Boxplot)', fontsize=14)
    plt.xlabel('RBM Layer', fontsize=12)
    plt.ylabel('Weight Value', fontsize=12)
    plt.grid(True, alpha=0.3, axis='y')
    plt.savefig('weight_distribution.png', dpi=300, bbox_inches='tight')
    plt.show()


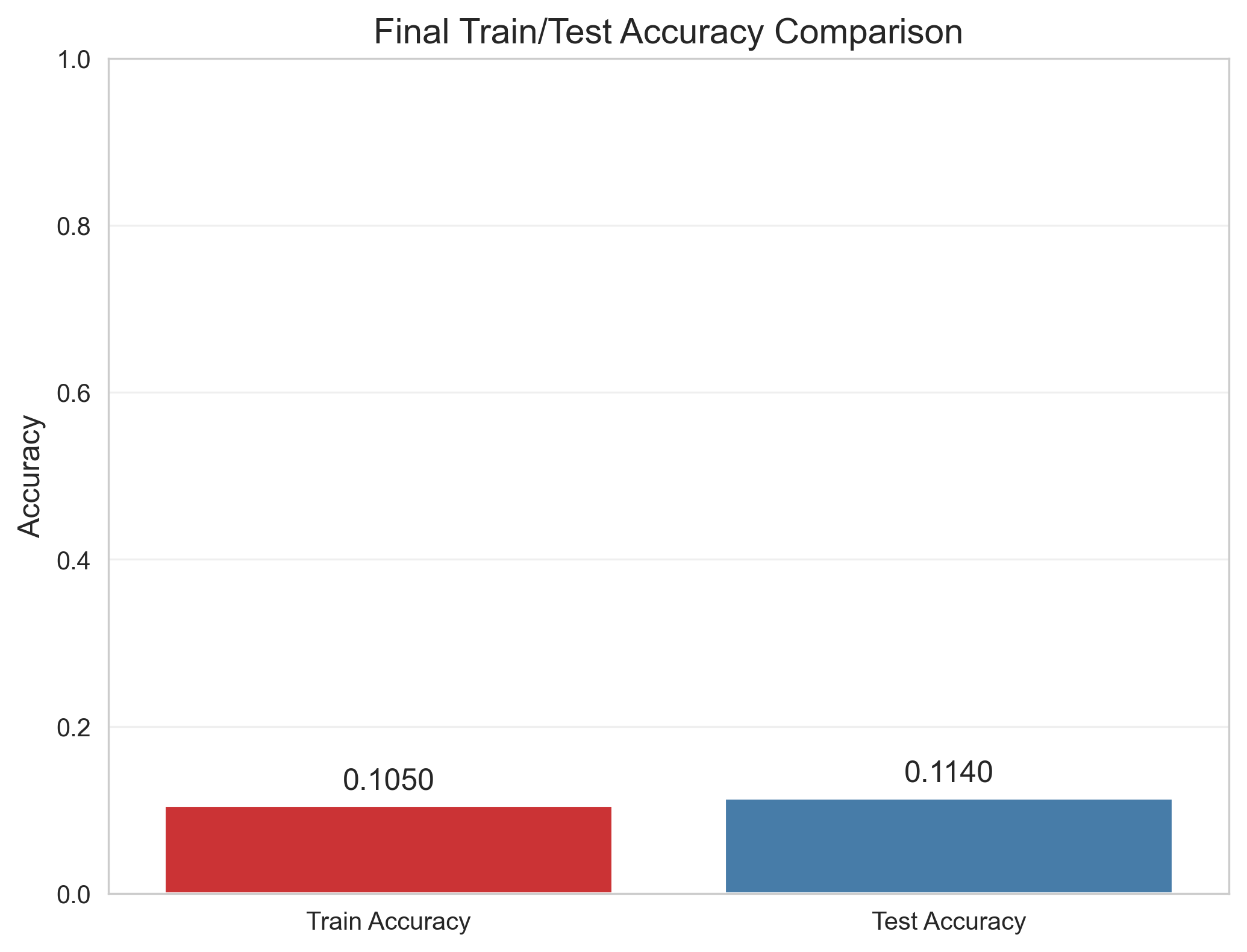
def plot_acc_bar(dbn):
    """绘制最后一轮训练/测试准确率对比柱状图"""
    if not dbn.finetune_train_acc or not dbn.finetune_test_acc:
        print("无准确率数据！")
        return

    last_train_acc = dbn.finetune_train_acc[-1]
    last_test_acc = dbn.finetune_test_acc[-1]

    plt.figure(figsize=(8, 6))
    sns.barplot(x=['Train Accuracy', 'Test Accuracy'], y=[last_train_acc, last_test_acc], palette='Set1')
    plt.title('Final Train/Test Accuracy Comparison', fontsize=14)
    plt.ylabel('Accuracy', fontsize=12)
    plt.ylim(0, 1)  # 准确率范围0-1
    # 标注数值
    plt.text(0, last_train_acc + 0.02, f'{last_train_acc:.4f}', ha='center', fontsize=12)
    plt.text(1, last_test_acc + 0.02, f'{last_test_acc:.4f}', ha='center', fontsize=12)
    plt.grid(True, alpha=0.3, axis='y')
    plt.savefig('final_acc_comparison.png', dpi=300, bbox_inches='tight')
    plt.show()


# -------------------------- 5. 加载数据集 --------------------------
def load_synthetic_dataset(batch_size=32, feature_dim=32, num_classes=10):
    """加载通用合成数据集"""
    train_dataset = SyntheticClassificationDataset(
        num_samples=10000, feature_dim=feature_dim, num_classes=num_classes, train=True
    )
    test_dataset = SyntheticClassificationDataset(
        num_samples=10000, feature_dim=feature_dim, num_classes=num_classes, train=False
    )

    train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
    test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
    return train_loader, test_loader


# -------------------------- 6. 主函数 --------------------------
if __name__ == "__main__":
    # 设备配置
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    print(f"Using device: {device}")

    # 超参数
    feature_dim = 32
    num_classes = 10
    hidden_dims = [64, 32, 16]
    batch_size = 32
    pretrain_lr = 0.01
    pretrain_epochs = 5
    finetune_lr = 0.001
    finetune_epochs = 8

    # 1. 加载数据集
    train_loader, test_loader = load_synthetic_dataset(
        batch_size=batch_size, feature_dim=feature_dim, num_classes=num_classes
    )

    # 2. 初始化 DBN
    dbn = DBN(
        input_dim=feature_dim,
        hidden_dims=hidden_dims,
        output_dim=num_classes,
        device=device
    ).to(device)

    # 3. 无监督预训练
    dbn.pretrain(train_loader, lr=pretrain_lr, epochs=pretrain_epochs, k=1)

    # 4. 有监督微调
    dbn.finetune(train_loader, test_loader, lr=finetune_lr, epochs=finetune_epochs)

    # 5. 保存模型
    torch.save(dbn.state_dict(), "dbn_generic_classification.pth")
    print("\nModel saved as 'dbn_generic_classification.pth'")

    # 6. 可视化结果
    print("\n===== 开始生成可视化图表 =====")
    # 基础可视化
    plot_rbm_recon_errors(dbn)  # RBM重构误差曲线
    plot_finetune_metrics(dbn)  # 微调损失/准确率曲线
    plot_rbm_weights(dbn, rbm_idx=0)  # 第一层RBM权重热力图
    plot_rbm_weights(dbn, rbm_idx=1)  # 第二层RBM权重热力图
    plot_confusion_matrix(dbn)  # 混淆矩阵
    plot_feature_distribution(dbn)  # 输入特征分布直方图
    plot_hidden_activation_dist(dbn)  # 隐藏层激活值分布
    plot_weight_distribution(dbn)  # 权重分布箱线图（修复后）
    plot_acc_bar(dbn)  # 最终准确率对比柱状图

    print("所有可视化图表已保存到当前目录！")

八、程序运行结果展示

Using device: cpu

===== 预训练第 1/3 层 RBM =====

RBM 1 训练: 20%|██ | 1/5 [00:00<00:00, 8.27it/s]RBM 1 Epoch 1, Reconstruction Error: 0.2502

RBM 1 训练: 40%|████ | 2/5 [00:00<00:00, 8.30it/s]RBM 1 Epoch 2, Reconstruction Error: 0.2503

RBM 1 Epoch 3, Reconstruction Error: 0.2503

RBM 1 训练: 80%|████████ | 4/5 [00:00<00:00, 8.44it/s]RBM 1 Epoch 4, Reconstruction Error: 0.2502

RBM 1 训练: 100%|██████████| 5/5 [00:00<00:00, 8.46it/s]

RBM 2 训练: 0%| | 0/5 [00:00<?, ?it/s]RBM 1 Epoch 5, Reconstruction Error: 0.2503

===== 预训练第 2/3 层 RBM =====

RBM 2 训练: 20%|██ | 1/5 [00:00<00:00, 7.91it/s]RBM 2 Epoch 1, Reconstruction Error: 0.2501

RBM 2 Epoch 2, Reconstruction Error: 0.2500

RBM 2 训练: 60%|██████ | 3/5 [00:00<00:00, 7.94it/s]RBM 2 Epoch 3, Reconstruction Error: 0.2501

RBM 2 Epoch 4, Reconstruction Error: 0.2501

RBM 2 训练: 100%|██████████| 5/5 [00:00<00:00, 7.97it/s]

RBM 3 训练: 0%| | 0/5 [00:00<?, ?it/s]RBM 2 Epoch 5, Reconstruction Error: 0.2500

===== 预训练第 3/3 层 RBM =====

RBM 3 Epoch 1, Reconstruction Error: 0.2499

RBM 3 训练: 40%|████ | 2/5 [00:00<00:00, 7.88it/s]RBM 3 Epoch 2, Reconstruction Error: 0.2499

RBM 3 Epoch 3, Reconstruction Error: 0.2499

RBM 3 训练: 80%|████████ | 4/5 [00:00<00:00, 7.88it/s]RBM 3 Epoch 4, Reconstruction Error: 0.2499

RBM 3 训练: 100%|██████████| 5/5 [00:00<00:00, 7.82it/s]

微调训练: 0%| | 0/8 [00:00<?, ?it/s]RBM 3 Epoch 5, Reconstruction Error: 0.2498

===== 开始微调 DBN =====

Epoch 1 | Train Loss: 2.3031 | Train Acc: 0.0915 | Test Loss: 2.3026 | Test Acc: 0.1060

Epoch 3 | Train Loss: 2.3022 | Train Acc: 0.1011 | Test Loss: 2.3022 | Test Acc: 0.1060

Epoch 5 | Train Loss: 2.3021 | Train Acc: 0.1050 | Test Loss: 2.3022 | Test Acc: 0.1145

Epoch 8 | Train Loss: 2.3019 | Train Acc: 0.1050 | Test Loss: 2.3022 | Test Acc: 0.1140

Model saved as 'dbn_generic_classification.pth'

===== 开始生成可视化图表 =====

微调训练: 100%|██████████| 8/8 [00:02<00:00, 3.08it/s]

所有可视化图表已保存到当前目录！

九、DBN 的现代意义与延伸

尽管 DBN 已不是当前主流模型，但它的核心思想影响深远：

预训练思想：启发了 BERT、GPT 等大模型的预训练 - 微调范式；
生成式建模：为 GAN、VAE 等现代生成模型奠定了理论基础；
深层特征学习：证明了深层网络能够学习更抽象、更具表达力的特征。

现代替代方案

分类任务：CNN（图像）、Transformer（文本 / 图像）；
生成任务：GAN（生成逼真样本）、VAE（概率生成）；
半监督学习：FixMatch、Virtual Adversarial Training（VAT）。

十、总结

深度信念网络是深度学习的 "开山鼻祖" 之一，其核心价值在于：

提出了 "预训练 + 微调" 的深层网络训练策略，解决了梯度消失问题；
证明了无监督学习能够自动提取高质量的多层特征；
兼具生成与判别能力，为后续模型提供了重要参考。

本文详细介绍了DBN的网络结构、RBM组件原理、训练流程（对比散度算法和微调方法），并提供了完整的Python实现代码，包括数据预处理、模型构建、训练过程和可视化分析。尽管DBN在主流任务中已被CNN、Transformer等模型取代，但其预训练思想和深层特征学习机制对现代深度学习发展产生了深远影响。