学懂导数、偏导数,再学微分就简单多了。这些知识是相通的,基本不需重新理解,动态和微观的观点仍然通用。
1 理解微分
前面已经学过,导数的表达式是这样的:
f ′ ( x ) = y ′ = d y d x = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 d y + o ( x ) Δ x f'(x) = y' = \frac{dy}{dx} = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{dy + o(x)}{\Delta x} f′(x)=y′=dxdy=limΔx→0ΔxΔy=limΔx→0Δxdy+o(x)
其中, o ( x ) o(x) o(x)表示一个比 d y dy dy高阶的无穷小,大小为 Δ y − d y \Delta y - dy Δy−dy。
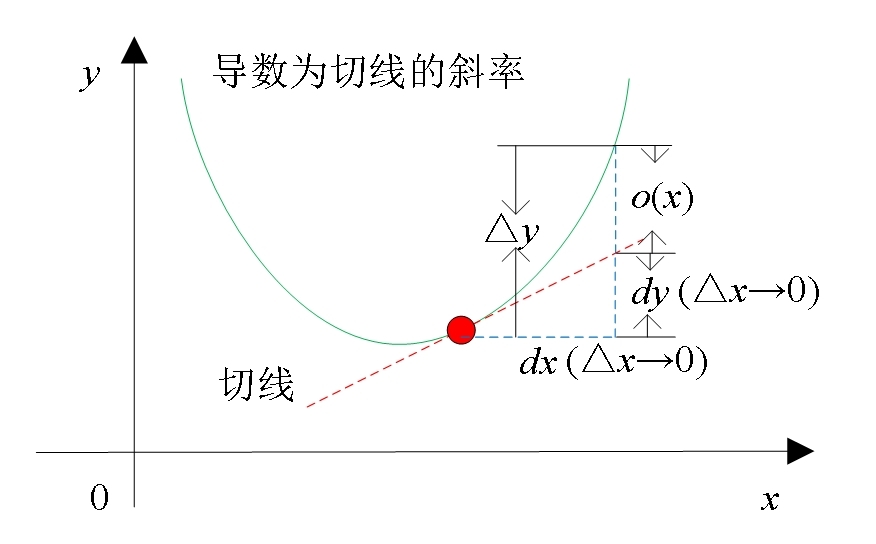
图1 导数的含义示意图
导数之所以可以用 d y d x \frac{dy}{dx} dxdy表示,根本原因在于它确实是 d y dy dy与 d x dx dx的比值。 d y dy dy与 d x dx dx就是微分 ,可分别理解为 x x x和 y y y的非常微小的量;而 Δ x \Delta x Δx与 Δ y \Delta y Δy分别表示 x x x与 y y y的变化量。可见,微分 d d d与 Δ \Delta Δ的内涵不同。但当 Δ x → 0 \Delta x \to 0 Δx→0时,可认为 Δ x = d x \Delta x = dx Δx=dx(从图1也可明显看出);从微观角度看, Δ y \Delta y Δy与 d y dy dy长度不同,但当 Δ x → 0 \Delta x \to 0 Δx→0时,由于 Δ y − d y = o ( x ) \Delta y - dy = o(x) Δy−dy=o(x),故可认为 Δ y \Delta y Δy等同于 d y dy dy。
要想看更多有趣的微积分故事、知识,请参见清华大学出版社的《人人可懂的微积分》。
微分的计算推导
根据导数的表达式做变换,可知:
d y = f ′ ( x ) d x = y ′ d x = lim Δ x → 0 Δ y Δ x d x = lim Δ x → 0 d y + o ( x ) Δ x d x = lim Δ x → 0 d y Δ x d x + lim Δ x → 0 o ( x ) Δ x d x = lim Δ x → 0 ( d y + o ( x ) ) dy = f'(x)dx = y'dx = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}dx = \lim_{\Delta x \to 0}\frac{dy + o(x)}{\Delta x}dx = \lim_{\Delta x \to 0}\frac{dy}{\Delta x}dx + \lim_{\Delta x \to 0}\frac{o(x)}{\Delta x}dx = \lim_{\Delta x \to 0}(dy + o(x)) dy=f′(x)dx=y′dx=limΔx→0ΔxΔydx=limΔx→0Δxdy+o(x)dx=limΔx→0Δxdydx+limΔx→0Δxo(x)dx=limΔx→0(dy+o(x))
| 学习点拨 | 注意在上述变换过程中,体验和感受 Δ x \Delta x Δx与 d x dx dx、 Δ y \Delta y Δy与 d y dy dy之间的细小差别及等同关系。建议结合图4-3来形象理解。 |
|---|
2 掌握微分的计算法则
根据公式 d y = f ′ ( x ) d x = y ′ d x dy = f'(x)dx = y'dx dy=f′(x)dx=y′dx,会计算导数则微分计算法则易理解掌握。列举5个稍复杂的计算法则:
- d ( u + v ) = d u + d v d(u + v) = du + dv d(u+v)=du+dv
- d ( u − v ) = d u − d v d(u - v) = du - dv d(u−v)=du−dv
- d ( u v ) = v d u + u d v d(uv) = vdu + udv d(uv)=vdu+udv
- d u v = v d u − u d v v 2 ( v ≠ 0 ) d\frac{u}{v} = \frac{vdu - udv}{v^2} (v \neq 0) dvu=v2vdu−udv(v=0)
- d ( 1 v ) = − 1 v 2 d v ( v ≠ 0 ) d\left(\frac{1}{v}\right) = -\frac{1}{v^2}dv (v \neq 0) d(v1)=−v21dv(v=0)
公式证明(以 d u v d\frac{u}{v} dvu为例)
根据 d y = f ′ ( x ) d x = y ′ d x dy = f'(x)dx = y'dx dy=f′(x)dx=y′dx,有:
d u v = ( u v ) ′ d x = u ′ v − u v ′ v 2 d x = d u d x v − u d v d x v 2 d x = v d u − u d v v 2 d\frac{u}{v} = \left(\frac{u}{v}\right)'dx = \frac{u'v - uv'}{v^2}dx = \frac{\frac{du}{dx}v - u\frac{dv}{dx}}{v^2}dx = \frac{vdu - udv}{v^2} dvu=(vu)′dx=v2u′v−uv′dx=v2dxduv−udxdvdx=v2vdu−udv
实例计算
例1:求函数 y = x 3 sin x y = x^3\sin x y=x3sinx的微分。
d y = d ( x 3 sin x ) = d ( x 3 ) sin x + x 3 d ( sin x ) = 3 x 2 sin x d x + x 3 cos x d x dy = d(x^3\sin x) = d(x^3)\sin x + x^3d(\sin x) = 3x^2\sin x dx + x^3\cos x dx dy=d(x3sinx)=d(x3)sinx+x3d(sinx)=3x2sinxdx+x3cosxdx
3 理解并计算偏微分和全微分
偏微分定义
以 f ( x , y ) f(x,y) f(x,y)为例, f ( x , y ) f(x,y) f(x,y)对 x x x的偏导数为 ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f,故其对 x x x的偏微分记为:
d f x = ∂ f ∂ x d x df_x = \frac{\partial f}{\partial x}dx dfx=∂x∂fdx
同理,对 y y y的偏微分记为:
d f y = ∂ f ∂ y d y df_y = \frac{\partial f}{\partial y}dy dfy=∂y∂fdy
全微分定义
全微分记为:
d f = d f x + d f y = ∂ f ∂ x d x + ∂ f ∂ y d y df = df_x + df_y = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy df=dfx+dfy=∂x∂fdx+∂y∂fdy
对于更多元的函数 f ( x 0 , ... , x n − 1 ) f(x_0, ..., x_{n-1}) f(x0,...,xn−1),全微分为:
d f = ∑ i = 0 n − 1 d f i = ∑ i = 0 n − 1 ∂ f ∂ x i d x i df = \sum_{i=0}^{n-1}df_i = \sum_{i=0}^{n-1}\frac{\partial f}{\partial x_i}dx_i df=∑i=0n−1dfi=∑i=0n−1∂xi∂fdxi
这些公式的表达看起来有点小复杂,关键在于怎么理解其内涵,理解了内涵,根本就无需记忆公式 。要想看更多有趣的微积分故事、知识,请参见清华大学出版社的《人人可懂的微积分》。
内涵理解
- ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f表示 x x x变化1个单位引发因变量的变化量, d f x = ∂ f ∂ x d x df_x = \frac{\partial f}{\partial x}dx dfx=∂x∂fdx表示 x x x变化 d x dx dx个单位引发的因变量变化量;
- ∂ f ∂ y \frac{\partial f}{\partial y} ∂y∂f表示 y y y变化1个单位引发因变量的变化量, d f y = ∂ f ∂ y d y df_y = \frac{\partial f}{\partial y}dy dfy=∂y∂fdy表示 y y y变化 d y dy dy个单位引发的因变量变化量;
- 全微分 d f df df数值上表示:在 X O Y XOY XOY平面中,两个自变量变化 ( d x , d y ) (dx, dy) (dx,dy)一共引发因变量的变化量。
| 答疑解惑 | 学生问:老师,全微分与方向导数长得有点像,两者有什么区别呢? 老师答:长得确实有点像,但两者有区别。方向导数求得的数值是沿 X O Y XOY XOY平面中方向导数指出的向量方向变化一个单位,引发因变量的变化量;而全微分引发因变量变化的起因是 ( d x , d y ) (dx, dy) (dx,dy)。可见两者变化起因不同,方向导数只考虑一个方向的变化,全微分综合各方向变化。此外,方向导数计算的是因变量随自变量的变化率;全微分计算的是因变量的变化值,通过自变量的偏导数与自变量微小变化量的线性组合近似表示因变量变化,体现函数在该点的局部线性近似性质。 |
|---|
实例计算
例2:求函数 z = x 2 + 3 x y + y 2 z = x^2 + 3xy + y^2 z=x2+3xy+y2的全微分。
∂ z ∂ x = 2 x + 3 y \frac{\partial z}{\partial x} = 2x + 3y ∂x∂z=2x+3y
∂ z ∂ y = 2 y + 3 x \frac{\partial z}{\partial y} = 2y + 3x ∂y∂z=2y+3x
rtial x} = 2x + 3y$
∂ z ∂ y = 2 y + 3 x \frac{\partial z}{\partial y} = 2y + 3x ∂y∂z=2y+3x
d z = ∂ f ∂ x d x + ∂ f ∂ y d y = ( 2 x + 3 y ) d x + ( 2 y + 3 x ) d y dz = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy = (2x + 3y)dx + (2y + 3x)dy dz=∂x∂fdx+∂y∂fdy=(2x+3y)dx+(2y+3x)dy