简介:
时间:2025
会议:AAAI
作者:Ming Li, Yongchun Gu, Yi Wang*, Yujie Fang, Lu Bai*, Xiaosheng Zhuang, Pietro Lio
摘要:
提出面向超图的双重同配比度量,实现结构-标签偏置的数值化评估;
构建面向异配场景的大规模、多领域基准数据集;
设计基于framelet变换的低通-高通双通道模型 HyperUFG,作为异配超图学习的强基线
创新点:
①提出并形式化超边同配比 Hedgc 与超节点同配比 Hnode
②构建面向异配场景的大规模、多领域超图基准集
③将framelet紧框架引入超图谱域,设计低通-高通可学习滤波器,兼顾同类平滑与异类判别
④实现 HyperUFG 模型,作为异配超图学习的强基线
引言:
研究背景:
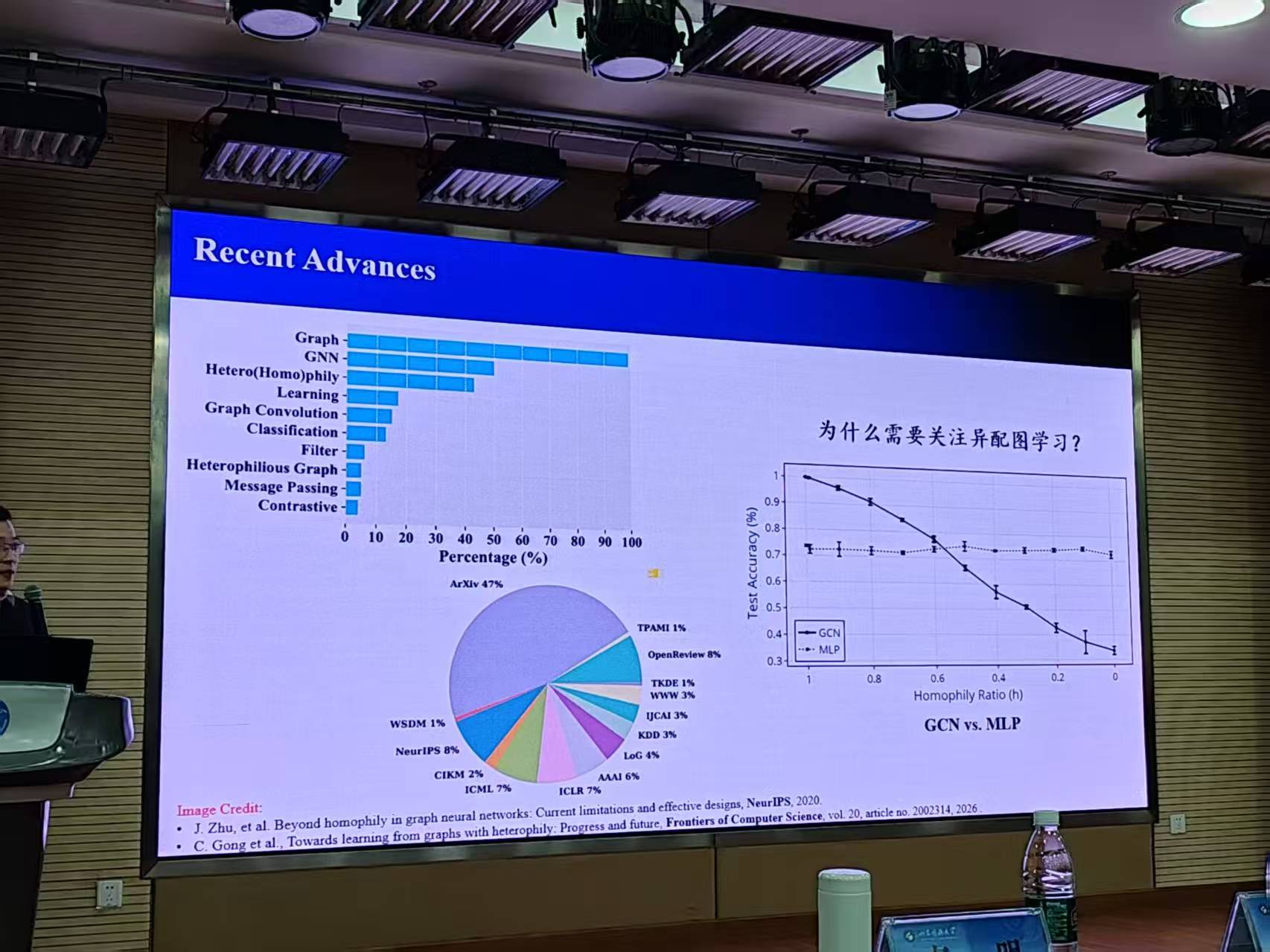
①超图对多实体交互建模具有天然优势,但主流 HNN基于"相邻节点标签相似"的同质假设
②图神经网络领域已证明当邻域标签分布差异大时,低通卷积会引入对立噪声,导致分类边界模糊;超图因一条超边可连接任意数量节点,异配问题更突出
关键观察:
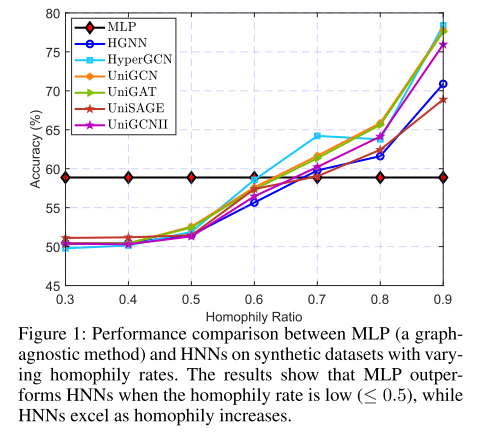
在 3-均匀合成超图上,将同配比 Hedgc 由 0.3 调至 0.9,观察到:
①所有 HNN 准确率随 Hedgc 单调上升
②Hedgc ≤0.5 时,MLP 领先 HNN
③Hedgc >0.5 后,HNN 反超 MLP
研究缺口:
Q1概念层:缺乏专用于超图的同配/异配度量
Q2 数据层:现有数据集(Congress、Walmart 等)同配比>0.5 且规模小、主题单一
Q3 模型层:尚无针对异配超图设计的专用网络
异质性超图的挑战:对合成数据的观察:
超图同配比度量:
超边同配比 Hedgc:
物理意义:随机抽取一条超边,其内部节点对属于同一类别的期望比例

超节点同配比 Hnode:
物理意义:随机抽查一个节点,在其所有关联超边中的平均同配水平

性质:
定义性质:
①当超图退化为普通图时,Hedgc 与 Hnode 分别等价于传统边同配与节点同配指标;
②取值 0→1,0.5 为随机分界线
③传统图指标直接迁移到超图会失真
定义区别:
|---------------------|---------|---------------------------|
| 指标 | 先做平均的对象 | 问题 |
| Hyperedge Homophily | 每条超边 | 该超边里同类节点对占比多少? |
| Node Homophily | 每个节点 | 该节点参加的所有超边里,遇到同类的平均比例是多少? |
同配超图vs异配超图:
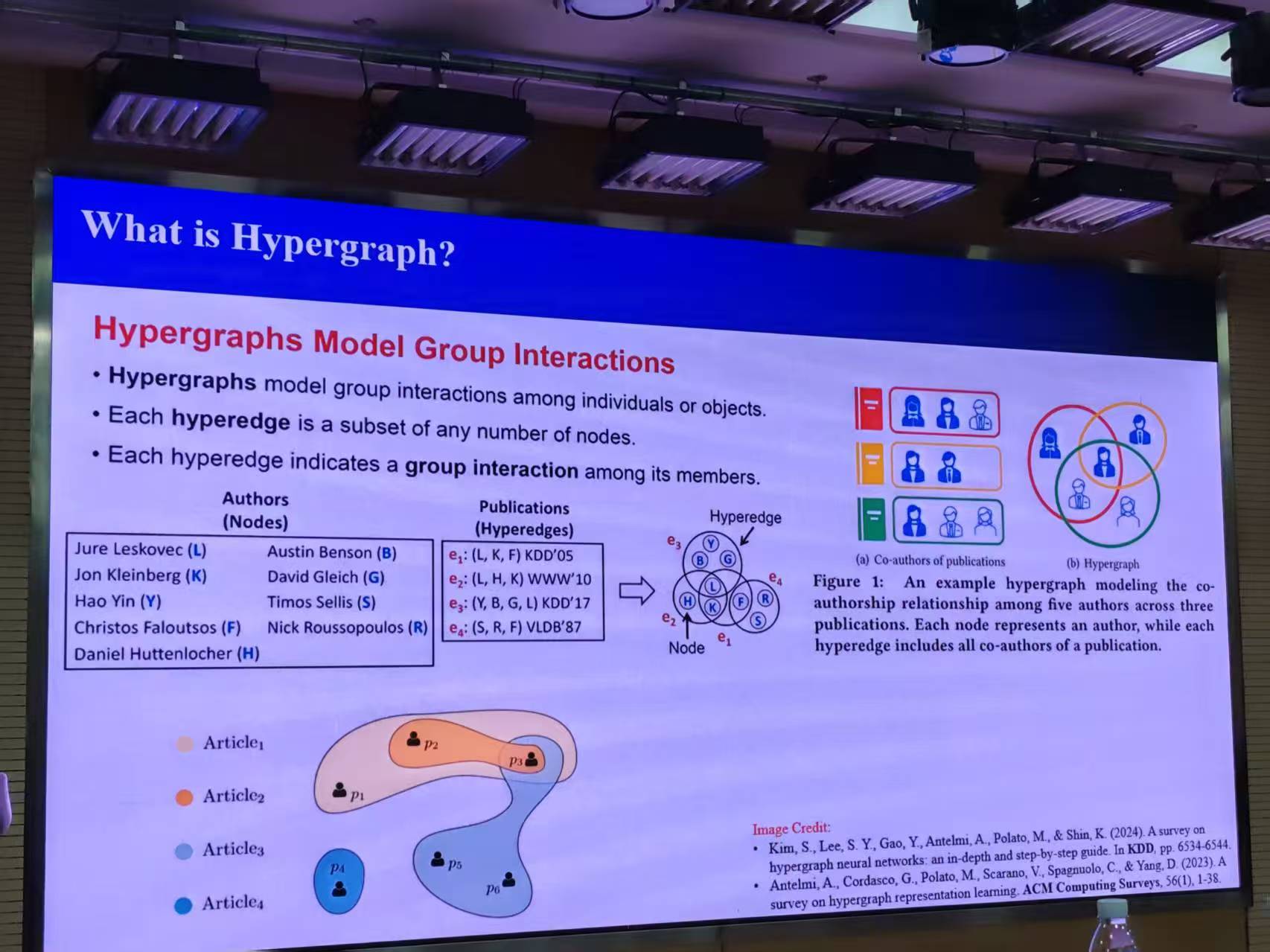

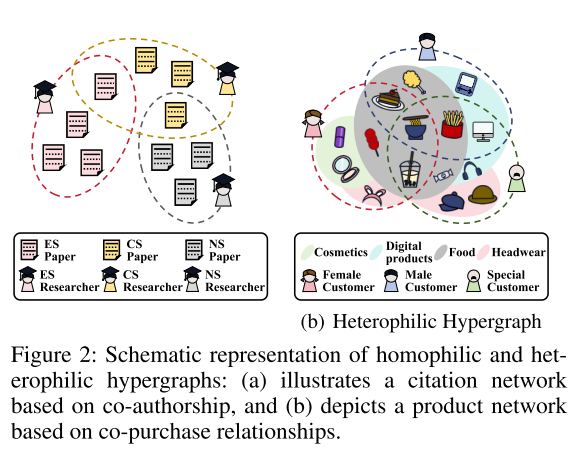
同配超图:
例子:合著网络 → 一条超边(一篇论文)里的作者大多来自同一研究领域
物理意义:物以类聚,同类节点聚集
异配超图:
例子:商品共购网络 → 一条超边(一次购物篮)里化妆品、数码、食品全都有,类别多
物理意义:追求多样性,同类节点不聚集
合成数据分析:
HSBM:

参数 (n,r,C,p,q):n=10000, r=3, C=2 clusters;同簇三元组以概率 p 生成超边,跨簇以概率 q 生成。通过 {p,q} 七组配置,得到 Hedgc∈[0.3,0.9]。

①:同簇更容易连接超边,更容易生成同质超图
②:同簇和跨簇差不多,生成更随机
③:跨簇更容易连接超边,更容易生成异质超图

主要结论:
①HNN 性能与 Hedgc 呈显著正相关
②Hedgc≤0.5 时,MLP 优于全部 HNN;Hedgc>0.5 后 HNN 反超
结论:在低同配区域,超边聚合会引入跨类噪声,传统"信息传递+非线性"范式失效。
异质超图的新基准:
构建准则:
①同配比<0.5(双指标验证)
②超图结构对任务显著相关(HNN 须优于 MLP)
③规模 10k--30k,可覆盖现有 HNN 显存上限
④多领域、特征维度与类别分布多样化
数据集描述:
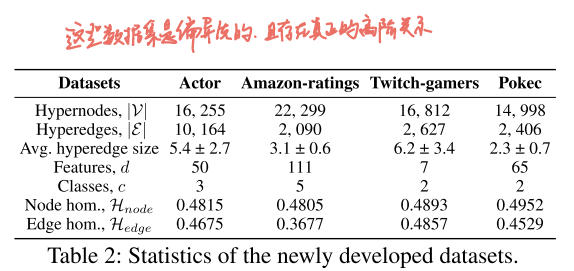
Actor:16 255 节点,10 164 超边,平均规模 5.4,Hedgc=0.467,3 类角色分类
Amazon-ratings:22 299 节点,2 090 超边,Hedgc=0.368,5 类评分档次预测
Twitch-gamers:16 812 节点,2 627 超边,Hedgc=0.486,2 类少儿适宜判别
Pokec:14 998 节点,2 406 超边,Hedgc=0.453,2 类性别分类
异质性HNN的新基线:
定义:
核心动机:
异配场景下,邻居往往不是同类;只做"平均/平滑"会把信号洗掉;需要同时建模低频(同类共性)和高频(异类差异)
符号谱域背景:
超图:
节点特征矩阵:
超图拉普拉斯(hypergraph Laplacian):
对做特征分解:
特征向量矩阵:
特征值对角矩阵:
直觉:
① 相当于把信号从"节点域"变到"频域"(谱域)
② 低频 ↔ 平滑/同配信息;高频 ↔ 变化剧烈/边界/异配信息
Framelet 系统:
关系:
引入 framelets(可以把它当作图小波的一类"框架"版本),关键是一个滤波器组 filter bank
scaling functions:
filter bank:
满足类似小波多分辨分析的关系:
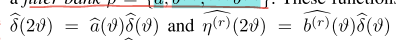
在谱域里定义一组"低通滤波器 + 多个高通滤波器",从而在不同尺度上分解超图信号
k 表示用了多少个高通滤波器(高频通道数)
低通 framelet & 高通 framelet:
给出在节点 处、以节点
为中心、尺度
的 framelet 基函数:
低通(Low-pass)framelet:
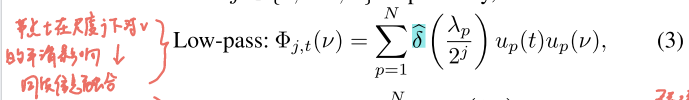
解释:
①对每个谱分量,用低通响应
去加权
②是谱基下从
到
的"影响形状"
③结果:代表"在尺度
上的平滑基",强调低频结构(同配友好)
高通(High-pass)framelet:
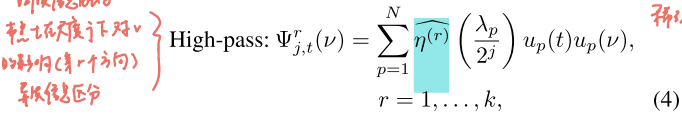
解释:
①和低通同构,但把滤波器换成高通
②高通强调信号变化、边界、差异------这正是异配场景需要保留的部分
framelet 系数把基函数作用到特征上:
基函数有了,要把它"投影"到实际信号上,得到系数矩阵:
低通系数:
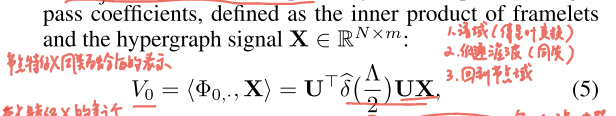
高通系数:
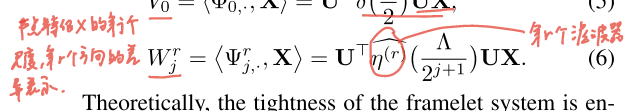
过程:
① 把节点特征变到谱域
②乘上滤波响应或
相当于"在频域筛选频段"
③再乘回回到节点域
④得到低频表示和各尺度高频表示
tight frame 条件+可逆性:
tightness(紧框架)条件:
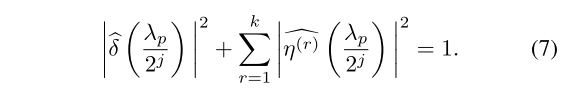
对每个频率点(每个特征值),低通能量 + 所有高通能量 = 1,这保证了:信息不会凭空丢失或重复膨胀------分解是稳定的、可逆的。
进一步写出可逆性(重构公式):

把信号拆成"低频 + 多尺度高频",但理论上还能拼回原信号,所以这是一个信息保真的分解框架。
把分解写成算子形式:
把 Eq.(5)(6) 里的"滤波+变换"抽象成分解算子:
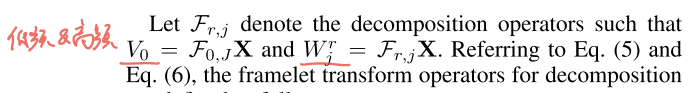
这一步的意义是后面做卷积时,直接用在不同通道/尺度上对
做变换,然后再用
合回去
用 Chebyshev 多项式近似:
谱方法的痛点是的特征分解很贵,所以作者用 Chebyshev 多项式去逼近滤波器,让它变成
的多项式,从而只需要稀疏矩阵乘法:
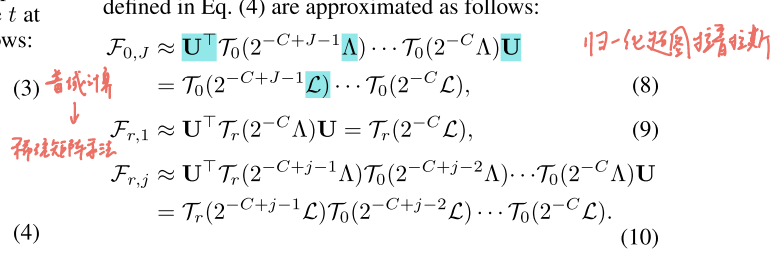
HyperUFG 卷积层:
把上述 framelet 分解系统做成一个"谱域卷积层",命名HyperUFG,并加入 GCNII 类似的两种技巧:
①initial residual(初始残差):把直接注入每层,缓解过平滑
②identity mapping(恒等映射):控制每层线性变换强度,稳定深层训练
卷积层定义:
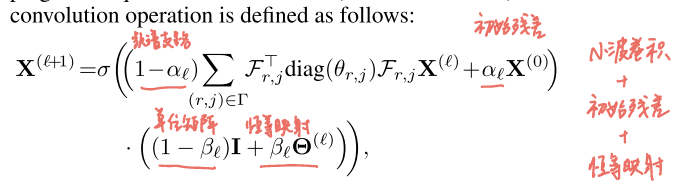
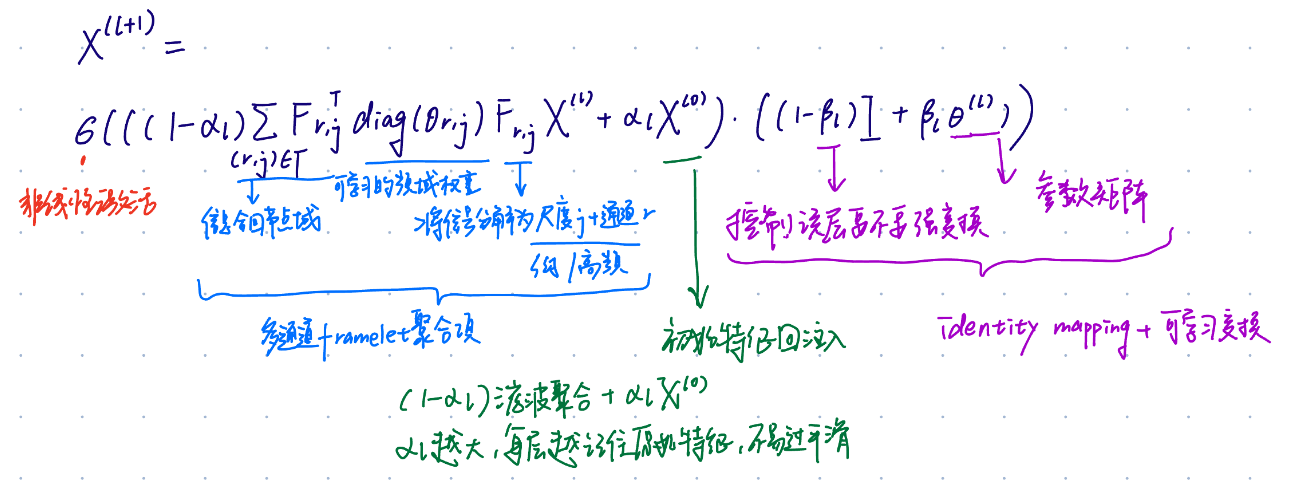
HyperUFG 对 heterophily 更友好:
低通部分增强同配邻居间的 "similarity"(让同类更接近);高通部分强调异配邻居间的 "distinguishable information"(把差异凸显出来),从而弥补传统空间 message passing 在 HHL 场景中"邻居聚合无效甚至有害"的问题。
实验:
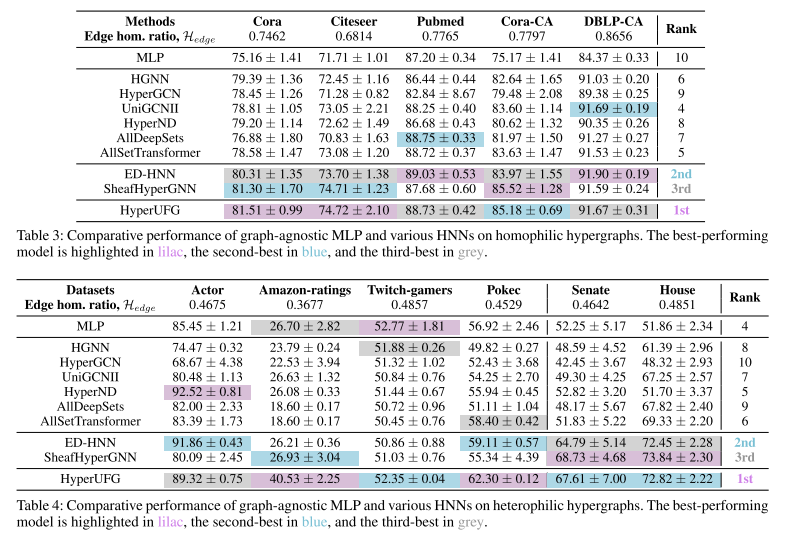
结论与未来工作:
结论:
①首次系统定义超图同配/异配度量,为后续研究提供量化工具
②发布四个大规模、多领域异配超图基准,结束"用同配数据集测异配模型"的尴尬
③HyperUFG 通过帧波低通-高通联合滤波,在同配、异配场景均实现 SOTA 或接近 SOTA,为异配超图学习提供可直接复用的强基线。
未来方向:
①百万节点级工业超图下的内存与可扩展性
②动态、有向、带权及超边特征场景下的帧波设计
③与 hyperbolic、simplex 等几何嵌入结合,探索更高阶结构偏差。