P3373 【模板】线段树 2
时间限制: 1.00s 内存限制: 125.00MB
复制 Markdown
中文
退出 IDE 模式
题目描述
如题,已知一个数列 a,你需要进行下面三种操作:
- 将某区间每一个数乘上 x;
- 将某区间每一个数加上 x;
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 n,q,m,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n 个用空格分隔的整数,其中第 i 个数字表示数列第 i 项的初始值 ai。
接下来 q 行每行包含若干个整数,表示一个操作,具体如下:
操作 1: 格式:1 x y k 含义:将区间 [x,y] 内每个数乘上 k。
操作 2: 格式:2 x y k 含义:将区间 [x,y] 内每个数加上 k。
操作 3: 格式:3 x y 含义:输出区间 [x,y] 内每个数的和对 m 取模所得的结果。
输出格式
输出包含若干行整数,即为所有操作 3 的结果。
输入输出样例
输入 #1复制运行
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4输出 #1复制运行
17
2说明/提示
【数据范围】
对于 30% 的数据:n≤8,q≤10。
对于 70% 的数据:n≤103,q≤104。
对于 100% 的数据:1≤n≤105,1≤q≤105,1≤ai,k≤104。
除样例外,m=571373。
(数据已经过加强 ^_^)
样例说明:
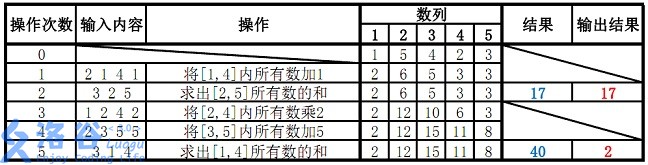
故输出应为 17、2(40mod38=2)。
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
long long a[N],n,m,mod;
struct SegmentTree{
long long l,r;
long long sum,add,mul;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define add(x) tree[x].add
#define mul(x) tree[x].mul
}tree[4*N];
void build(int p,int l,int r){
l(p)=l,r(p)=r,mul(p)=1;
if(l==r){sum(p)=a[l]%mod;return;}
int mid = (l+r)>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
sum(p)=(sum(p*2)+sum(p*2+1))%mod;
}
void spread(int p){
sum(p*2)=(sum(p*2)*mul(p)+add(p)*(r(p*2)-l(p*2)+1))%mod; //更新左子节点信息
sum(p*2+1)=(sum(p*2+1)*mul(p)+add(p)*(r(p*2+1)-l(p*2+1)+1))%mod; //更新右子节点信息
mul(p*2)=(mul(p*2)*mul(p))%mod;
mul(p*2+1)=(mul(p*2+1)*mul(p))%mod;
add(p*2)=(add(p*2)*mul(p)+add(p))%mod; //左子节点加延迟标记
add(p*2+1)=(add(p*2+1)*mul(p)+add(p))%mod; //右子节点加延迟标记
add(p)=0;
mul(p)=1;
}
void changemul(int p,int l,int r,int d){
if(l<=l(p)&&r>=r(p)){ //完全覆盖
sum(p)=sum(p)*d%mod; //更新节点信息
add(p)=add(p)*d%mod; //延迟标记
mul(p)=mul(p)*d%mod;
return;
}
spread(p);
int mid=(l(p)+r(p))>>1;
if(l<=mid)changemul(p*2,l,r,d);
if(r>mid)changemul(p*2+1,l,r,d);
sum(p)=(sum(p*2)+sum(p*2+1))%mod;
}
void changeadd(int p,int l,int r,int d){
if(l<=l(p)&&r>=r(p)){ //完全覆盖
sum(p)=(sum(p)+1LL*d*(r(p)-l(p)+1))%mod; //更新节点信息
add(p)=(add(p)+d)%mod; //延迟标记
return;
}
spread(p);
int mid=(l(p)+r(p))>>1;
if(l<=mid)changeadd(p*2,l,r,d);
if(r>mid)changeadd(p*2+1,l,r,d);
sum(p)=(sum(p*2)+sum(p*2+1))%mod;
}
long long query(int p,int l,int r){
if(l<=l(p)&&r>=r(p))return sum(p);
spread(p); //下传延迟标记
int mid=(l(p)+r(p))>>1;
long long val=0;
if(l<=mid)val=(val+query(p*2,l,r))%mod;
if(r>mid)val=(val+query(p*2+1,l,r))%mod;
return val;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>mod;
for(int i=1;i<=n;i++)cin>>a[i];
build(1,1,n);
for(int i=1;i<=m;i++){
int op;cin>>op;
if(op==1){
long long l,r,k;
cin>>l>>r>>k;
changemul(1,l,r,k);
}else if (op==2){
int l,r,k;
cin>>l>>r>>k;
changeadd(1,l,r,k);
}else {
int l,r;
cin>>l>>r;
cout<<query(1,l,r)%mod<<'\n';
}
}
return 0;
}