目录
九、自组织映射神经网络的Python代码完整实现（代码会自动下载鸢尾花数据集）
一、引言
自组织映射（Self-Organizing Map, SOM），又称 Kohonen 网络，是 1982 年由芬兰学者 Teuvo Kohonen 提出的无监督学习神经网络，核心是将高维数据非线性映射到低维（常为二维）网格并保持拓扑结构，兼具聚类、降维和可视化能力。本文将详细介绍自组织映射神经网络的基本原理以及Python代码完整实现。
二、核心原理与网络结构
SOM 基于竞争学习与拓扑保持机制，通过 "竞争 - 合作 - 自适应" 三阶段循环实现自组织学习，其结构简洁且功能明确。
- 网络结构
- 输入层：接收高维输入向量，神经元数量等于数据维度，无计算仅负责数据传递。
- 输出层：呈规则网格（常见二维矩形 / 六边形），每个神经元对应一个与输入维度相同的权重向量，是映射与计算核心，神经元位置决定拓扑关系。
- 核心机制
- 竞争机制：输入样本与所有输出神经元权重向量计算距离（常用欧氏距离），距离最小者为获胜神经元（BMU）。
- 合作机制：BMU 通过邻域函数（如高斯函数）激活周围神经元，邻域范围随训练迭代逐渐收缩。
- 自适应机制：BMU 及其邻域内神经元按更新公式调整权重，使权重向输入样本靠拢，学习率随迭代衰减。权重更新公式：
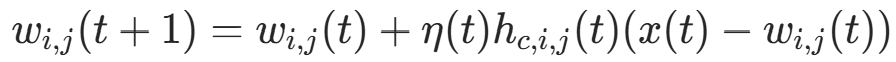
其中η(t)为学习率，为邻域函数，x(t)为输入样本，
为神经元权重。
三、完整训练流程
- 初始化 ：随机初始化输出层所有神经元权重向量（常与输入数据同分布），设置初始学习率
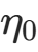、初始邻域半径
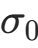、最大迭代次数T。 - 迭代训练（竞争→合作→自适应）
- 随机选取输入样本x。
- 计算x与各输出神经元权重的距离，确定 BMU。
- 计算邻域函数
，确定参与更新的神经元范围。
- 按权重更新公式调整 BMU 及邻域内神经元权重。
- 更新学习率
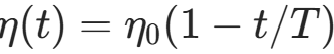与邻域半径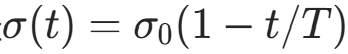
，随迭代线性衰减。
- 终止条件：迭代达到最大次数，或权重、学习率 / 邻域半径变化小于设定阈值，网络收敛。
四、关键特性
| 特性 | 说明 |
|---|---|
| 无监督学习 | 无需标注数据，仅通过数据内在特征完成映射与聚类 |
| 拓扑保持性 | 高维相似样本在低维映射空间中位置相邻，区别于 K-Means 等传统聚类 |
| 非线性映射 | 实现高维到低维的非线性降维，保留数据流形结构 |
| 可视化优势 | 二维映射结果可直观呈现数据分布与聚类情况，便于分析 |
| 竞争学习 | 神经元间竞争响应输入，BMU 主导权重更新，提升对同类数据敏感度 |
五、优缺点
- 优点
- 兼具降维、聚类与可视化功能，适合高维数据探索。
- 拓扑保持性有助于发现数据潜在结构与关联。
- 无监督学习，降低数据标注成本。
- 缺点
- 训练时间随输出层神经元数量增加而显著增长。
- 超参数（网格大小、学习率、邻域半径等）需经验调优，影响结果稳定性。
- 对噪声敏感，需预处理数据。
- 聚类结果受初始权重影响，可能陷入局部最优，可通过多次初始化缓解。
六、典型应用场景
- 数据可视化与探索：将高维数据（如基因表达、图像特征）映射到二维平面，直观展示数据分布与聚类，辅助发现潜在模式。
- 聚类分析：用于客户分群、文本聚类、异常检测等，如根据用户行为特征划分客户群体。
- 特征提取与降维：作为预处理步骤，提取关键特征并降低数据维度，为后续分类 / 回归任务提供高质量输入。
- 信号处理与模式识别：应用于语音识别、图像处理、故障诊断等，如语音信号特征映射与分类。
- 推荐系统：通过用户 / 物品特征映射，挖掘相似用户 / 物品，实现精准推荐。
七、与相关算法对比
| 算法 | 核心差异 | 优势 | 劣势 |
|---|---|---|---|
| SOM | 拓扑保持，非线性映射 | 可视化好，揭示数据关联 | 训练慢，超参数敏感 |
| K-Means | 硬聚类，无拓扑保持 | 训练快，易实现 | 聚类数需预设，丢失拓扑信息 |
| PCA | 线性降维，无聚类 | 计算高效，去冗余 | 仅线性映射，无法处理非线性数据 |
| t-SNE | 非线性降维，可视化优 | 降维效果好，适合可视化 | 训练慢，对参数敏感 |
八、实现要点与优化方向
- 数据预处理：对输入数据标准化 / 归一化，消除量纲影响，提升训练稳定性。
- 超参数选择
- 网格大小：根据数据规模与聚类粒度调整，常用8×8、10×10等。
- 学习率与邻域半径：初始值需合理，衰减策略可采用线性或指数衰减。
- 优化策略
- 批量训练：每次迭代使用多个样本，提升训练效率。
- 并行计算：利用 GPU 加速距离计算与权重更新，缩短训练时间。
- 初始化优化：基于数据分布初始化权重，降低局部最优概率。
九、自组织映射神经网络的Python代码完整实现（代码会自动下载鸢尾花数据集）
python
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from matplotlib.gridspec import GridSpec
import time
import pandas as pd
import json
import os
from minisom import MiniSom # 导入minisom库
# ====================== 基础配置 ======================
# 配置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
# 创建结果保存目录
save_dir = "som_iris_results"
os.makedirs(save_dir, exist_ok=True)
# ====================== 1. 手动实现SOM类（保留增强版） ======================
class SelfOrganizingMapManual:
"""手动实现SOM"""
def __init__(self, x_dim, y_dim, input_len, sigma=1.0, learning_rate=0.5, random_seed=None):
if random_seed is not None:
np.random.seed(random_seed)
self.x_dim = x_dim
self.y_dim = y_dim
self.input_len = input_len
self.initial_sigma = sigma
self.initial_lr = learning_rate
self.weights = np.random.rand(x_dim, y_dim, input_len)
self.neuron_coords = np.array([(i, j) for i in range(x_dim) for j in range(y_dim)]).reshape(x_dim, y_dim, 2)
self.learning_rates = []
self.sigmas = []
self.quantization_errors = []
self.training_time = 0
def _find_bmu(self, x):
distances = np.linalg.norm(self.weights - x, axis=2)
bmu_idx = np.unravel_index(np.argmin(distances), distances.shape)
min_distance = distances[bmu_idx]
return bmu_idx, min_distance
def _decay_functions(self, iteration, max_iter):
lr = self.initial_lr * np.exp(-iteration / max_iter)
sigma = self.initial_sigma * np.exp(-iteration / max_iter)
return lr, sigma
def _gaussian_neighborhood(self, bmu_coord, sigma):
bmu_distances = np.linalg.norm(self.neuron_coords - bmu_coord, axis=2)
neighborhood = np.exp(-(bmu_distances ** 2) / (2 * sigma ** 2))
return neighborhood
def update_weights(self, x, iteration, max_iter):
bmu_coord, min_distance = self._find_bmu(x)
lr, sigma = self._decay_functions(iteration, max_iter)
neighborhood = self._gaussian_neighborhood(bmu_coord, sigma)
neighborhood = neighborhood[:, :, np.newaxis]
self.weights += lr * neighborhood * (x - self.weights)
self.learning_rates.append(lr)
self.sigmas.append(sigma)
self.quantization_errors.append(min_distance)
def train(self, data, num_iteration):
start_time = time.time()
data_shuffled = data.copy()
for i in range(num_iteration):
x = data_shuffled[np.random.randint(0, len(data))]
self.update_weights(x, i, num_iteration)
self.training_time = time.time() - start_time
self.final_quantization_error = np.mean(self.quantization_errors)
def distance_map(self):
umatrix = np.zeros((self.x_dim, self.y_dim))
for i in range(self.x_dim):
for j in range(self.y_dim):
neighbors = []
if i > 0: neighbors.append(self.weights[i-1, j])
if i < self.x_dim-1: neighbors.append(self.weights[i+1, j])
if j > 0: neighbors.append(self.weights[i, j-1])
if j < self.y_dim-1: neighbors.append(self.weights[i, j+1])
if neighbors:
umatrix[i, j] = np.mean(np.linalg.norm(self.weights[i,j] - np.array(neighbors), axis=1))
return umatrix
def get_neuron_stats(self, data, target):
num_classes = len(np.unique(target))
neuron_samples = np.zeros((self.x_dim, self.y_dim), dtype=int)
neuron_class_dist = np.zeros((self.x_dim, self.y_dim, num_classes))
for x, cls in zip(data, target):
bmu, _ = self._find_bmu(x)
neuron_samples[bmu] += 1
neuron_class_dist[bmu, cls] += 1
return neuron_samples, neuron_class_dist
# ====================== 2. minisom库封装类 ======================
class SelfOrganizingMapMiniSom:
"""minisom库封装"""
def __init__(self, x_dim, y_dim, input_len, sigma=1.0, learning_rate=0.5, random_seed=None):
# 初始化minisom核心对象
self.som = MiniSom(x=x_dim, y=y_dim, input_len=input_len, sigma=sigma,
learning_rate=learning_rate, random_seed=random_seed)
self.x_dim = x_dim
self.y_dim = y_dim
self.input_len = input_len
self.initial_sigma = sigma
self.initial_lr = learning_rate
# 对齐手动版的记录变量
self.learning_rates = []
self.sigmas = []
self.quantization_errors = []
self.training_time = 0
self.final_quantization_error = 0
def _find_bmu(self, x):
"""对齐手动版的BMU查找接口"""
bmu_idx = self.som.winner(x) # minisom的winner方法返回BMU坐标
min_distance = np.linalg.norm(self.som.get_weights()[bmu_idx] - x)
return bmu_idx, min_distance
def train(self, data, num_iteration):
"""训练（记录学习率、邻域半径、量化误差，对齐手动版）"""
start_time = time.time()
# 手动记录训练过程（模拟minisom的内部衰减）
for i in range(num_iteration):
# 随机选样本
x = data[np.random.randint(0, len(data))]
# 记录量化误差
_, min_distance = self._find_bmu(x)
self.quantization_errors.append(min_distance)
# 计算衰减后的学习率和邻域半径（和手动版一致）
lr = self.initial_lr * np.exp(-i / num_iteration)
sigma = self.initial_sigma * np.exp(-i / num_iteration)
self.learning_rates.append(lr)
self.sigmas.append(sigma)
# 执行minisom的训练
self.som.train_random(data, num_iteration)
# 记录时间和最终误差
self.training_time = time.time() - start_time
self.final_quantization_error = np.mean(self.quantization_errors)
def distance_map(self):
"""对齐手动版的U-Matrix接口"""
return self.som.distance_map()
def get_neuron_stats(self, data, target):
"""对齐手动版的神经元统计接口"""
num_classes = len(np.unique(target))
neuron_samples = np.zeros((self.x_dim, self.y_dim), dtype=int)
neuron_class_dist = np.zeros((self.x_dim, self.y_dim, num_classes))
for x, cls in zip(data, target):
bmu, _ = self._find_bmu(x)
neuron_samples[bmu] += 1
neuron_class_dist[bmu, cls] += 1
return neuron_samples, neuron_class_dist
@property
def weights(self):
"""对齐手动版的权重属性"""
return self.som.get_weights()
# ====================== 3. 可视化函数（通用，支持双版本） ======================
def plot_som_analysis(som_model, data_scaled, target, feature_names, class_names, title_prefix, save_path):
"""通用SOM可视化函数"""
# 统计神经元信息
neuron_samples, neuron_class_dist = som_model.get_neuron_stats(data_scaled, target)
# 计算类别纯度
neuron_purity = np.zeros((som_model.x_dim, som_model.y_dim))
for i in range(som_model.x_dim):
for j in range(som_model.y_dim):
total = neuron_samples[i, j]
if total > 0:
neuron_purity[i, j] = np.max(neuron_class_dist[i, j]) / total
else:
neuron_purity[i, j] = 0
# 创建可视化
fig = plt.figure(figsize=(18, 20))
gs = GridSpec(3, 2, figure=fig, height_ratios=[1, 1, 1.2])
# 1. 训练过程监控
ax1 = fig.add_subplot(gs[0, 0])
ax1.plot(som_model.learning_rates, label='学习率', color='blue', linewidth=2)
ax1.plot(np.array(som_model.sigmas)/som_model.initial_sigma*som_model.initial_lr,
label='邻域半径（归一化）', color='orange', linewidth=2)
ax1.plot(np.array(som_model.quantization_errors)/np.max(som_model.quantization_errors)*som_model.initial_lr,
label='量化误差（归一化）', color='red', linestyle='--', linewidth=2)
ax1.set_title('SOM训练过程监控', fontsize=14, fontweight='bold')
ax1.set_xlabel('迭代次数', fontsize=12)
ax1.set_ylabel('数值（归一化）', fontsize=12)
ax1.legend(fontsize=10)
ax1.grid(alpha=0.3)
# 2. U-Matrix距离图
ax2 = fig.add_subplot(gs[0, 1])
umatrix = som_model.distance_map()
im2 = ax2.pcolor(umatrix.T, cmap='coolwarm', shading='auto')
ax2.set_title('SOM距离图（U-Matrix）', fontsize=14, fontweight='bold')
ax2.set_xlabel('神经元X坐标', fontsize=12)
ax2.set_ylabel('神经元Y坐标', fontsize=12)
cbar2 = plt.colorbar(im2, ax=ax2)
cbar2.set_label('神经元与邻域的平均距离', fontsize=10)
# 3. 神经元样本数量
ax3 = fig.add_subplot(gs[1, 0])
im3 = ax3.pcolor(neuron_samples.T, cmap='Blues', shading='auto')
for i in range(som_model.x_dim):
for j in range(som_model.y_dim):
ax3.text(i+0.5, j+0.5, str(neuron_samples[i,j]),
ha='center', va='center', fontsize=8, fontweight='bold')
ax3.set_title('神经元样本数量分布', fontsize=14, fontweight='bold')
ax3.set_xlabel('神经元X坐标', fontsize=12)
ax3.set_ylabel('神经元Y坐标', fontsize=12)
cbar3 = plt.colorbar(im3, ax=ax3)
cbar3.set_label('样本数量', fontsize=10)
# 4. 类别纯度热力图
ax4 = fig.add_subplot(gs[1, 1])
im4 = ax4.pcolor(neuron_purity.T, cmap='Greens', vmin=0, vmax=1, shading='auto')
for i in range(som_model.x_dim):
for j in range(som_model.y_dim):
if neuron_samples[i,j] > 0:
ax4.text(i+0.5, j+0.5, f'{neuron_purity[i,j]:.2f}',
ha='center', va='center', fontsize=8, fontweight='bold')
ax4.set_title('神经元类别纯度（最大类别占比）', fontsize=14, fontweight='bold')
ax4.set_xlabel('神经元X坐标', fontsize=12)
ax4.set_ylabel('神经元Y坐标', fontsize=12)
cbar4 = plt.colorbar(im4, ax=ax4)
cbar4.set_label('纯度（0=混杂，1=纯类别）', fontsize=10)
# 5. 神经元权重特征分布
ax5 = fig.add_subplot(gs[2, 0])
weights_flat = som_model.weights.reshape(-1, som_model.input_len)
im5 = ax5.pcolor(weights_flat.T, cmap='viridis', shading='auto')
ax5.set_yticks(np.arange(som_model.input_len)+0.5)
ax5.set_yticklabels(feature_names, fontsize=10)
ax5.set_xticks(np.arange(0, som_model.x_dim*som_model.y_dim, 10)+5)
ax5.set_xticklabels([f'({i},0)' for i in range(som_model.x_dim)], fontsize=8)
ax5.set_title('神经元权重特征分布', fontsize=14, fontweight='bold')
ax5.set_xlabel('神经元（按X=0~9,Y=0~9顺序）', fontsize=12)
ax5.set_ylabel('鸢尾花特征', fontsize=12)
cbar5 = plt.colorbar(im5, ax=ax5)
cbar5.set_label('标准化后的特征权重', fontsize=10)
# 6. 类别映射图
ax6 = fig.add_subplot(gs[2, 1])
ax6.pcolor(umatrix.T, cmap='coolwarm', alpha=0.3, shading='auto')
markers = ['o', 's', 'D']
colors = ['red', 'green', 'blue']
for cls in range(3):
cls_data = data_scaled[target == cls]
bmu_coords = [som_model._find_bmu(x)[0] for x in cls_data]
bmu_x = [c[0]+0.5 for c in bmu_coords]
bmu_y = [c[1]+0.5 for c in bmu_coords]
ax6.scatter(bmu_x, bmu_y, marker=markers[cls], color=colors[cls],
label=class_names[cls], s=60, edgecolors='black', alpha=0.8)
ax6.set_title('SOM类别映射图', fontsize=14, fontweight='bold')
ax6.set_xlabel('神经元X坐标', fontsize=12)
ax6.set_ylabel('神经元Y坐标', fontsize=12)
ax6.legend(fontsize=10, loc='upper right')
# 整体标题
fig.suptitle(f'{title_prefix} - 鸢尾花数据集SOM深度分析', fontsize=18, fontweight='bold')
plt.tight_layout()
# 保存图表
plt.savefig(save_path, dpi=300, bbox_inches='tight')
plt.show()
# 返回纯度用于对比
return np.mean(neuron_purity[neuron_samples > 0])
# ====================== 4. 数据加载与预处理 ======================
iris = load_iris()
data = iris.data
target = iris.target
feature_names = iris.feature_names
class_names = iris.target_names
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
# ====================== 5. 训练双版本SOM ======================
# 公共参数
som_x, som_y = 10, 10
input_len = data_scaled.shape[1]
sigma = 1.0
learning_rate = 0.5
max_iter = 1000
random_seed = 42
# 5.1 训练手动版
print("开始训练手动实现的SOM...")
som_manual = SelfOrganizingMapManual(x_dim=som_x, y_dim=som_y, input_len=input_len,
sigma=sigma, learning_rate=learning_rate, random_seed=random_seed)
som_manual.train(data_scaled, num_iteration=max_iter)
# 手动版可视化+保存
manual_avg_purity = plot_som_analysis(
som_model=som_manual,
data_scaled=data_scaled,
target=target,
feature_names=feature_names,
class_names=class_names,
title_prefix="手动实现版",
save_path=os.path.join(save_dir, "som_manual_iris.png")
)
# 5.2 训练minisom版
print("开始训练minisom库版SOM...")
som_minisom = SelfOrganizingMapMiniSom(x_dim=som_x, y_dim=som_y, input_len=input_len,
sigma=sigma, learning_rate=learning_rate, random_seed=random_seed)
som_minisom.train(data_scaled, num_iteration=max_iter)
# minisom版可视化+保存
minisom_avg_purity = plot_som_analysis(
som_model=som_minisom,
data_scaled=data_scaled,
target=target,
feature_names=feature_names,
class_names=class_names,
title_prefix="minisom库版",
save_path=os.path.join(save_dir, "som_minisom_iris.png")
)
# ====================== 6. 双版本对比 ======================
# 6.1 量化对比表
comparison_data = {
"指标": ["最终平均量化误差", "平均类别纯度", "训练时间（秒）", "初始学习率", "初始邻域半径", "迭代次数"],
"手动实现版": [
round(som_manual.final_quantization_error, 4),
round(manual_avg_purity, 4),
round(som_manual.training_time, 4),
som_manual.initial_lr,
som_manual.initial_sigma,
max_iter
],
"minisom库版": [
round(som_minisom.final_quantization_error, 4),
round(minisom_avg_purity, 4),
round(som_minisom.training_time, 4),
som_minisom.initial_lr,
som_minisom.initial_sigma,
max_iter
]
}
# 保存对比表为CSV
comparison_df = pd.DataFrame(comparison_data)
comparison_df.to_csv(os.path.join(save_dir, "som_comparison.csv"), index=False, encoding="utf-8-sig")
# 6.2 打印对比结果
print("\n====================== 双版本SOM对比结果 ======================")
print(comparison_df.to_string(index=False))
# 6.3 核心结果持久化（JSON）
results = {
"手动版": {
"final_quantization_error": som_manual.final_quantization_error,
"avg_class_purity": manual_avg_purity,
"training_time": som_manual.training_time,
"neuron_samples": som_manual.get_neuron_stats(data_scaled, target)[0].tolist()
},
"minisom版": {
"final_quantization_error": som_minisom.final_quantization_error,
"avg_class_purity": minisom_avg_purity,
"training_time": som_minisom.training_time,
"neuron_samples": som_minisom.get_neuron_stats(data_scaled, target)[0].tolist()
},
"参数配置": {
"som_size": f"{som_x}x{som_y}",
"sigma": sigma,
"learning_rate": learning_rate,
"max_iter": max_iter
}
}
with open(os.path.join(save_dir, "som_results.json"), "w", encoding="utf-8") as f:
json.dump(results, f, ensure_ascii=False, indent=4)
# 6.4 训练时间对比可视化
fig, ax = plt.subplots(figsize=(8, 5))
methods = ["手动实现版", "minisom库版"]
times = [som_manual.training_time, som_minisom.training_time]
colors = ["#1f77b4", "#ff7f0e"]
bars = ax.bar(methods, times, color=colors, width=0.6)
# 添加数值标签
for bar, t in zip(bars, times):
ax.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.01,
f"{t:.4f}秒", ha='center', va='bottom', fontweight='bold')
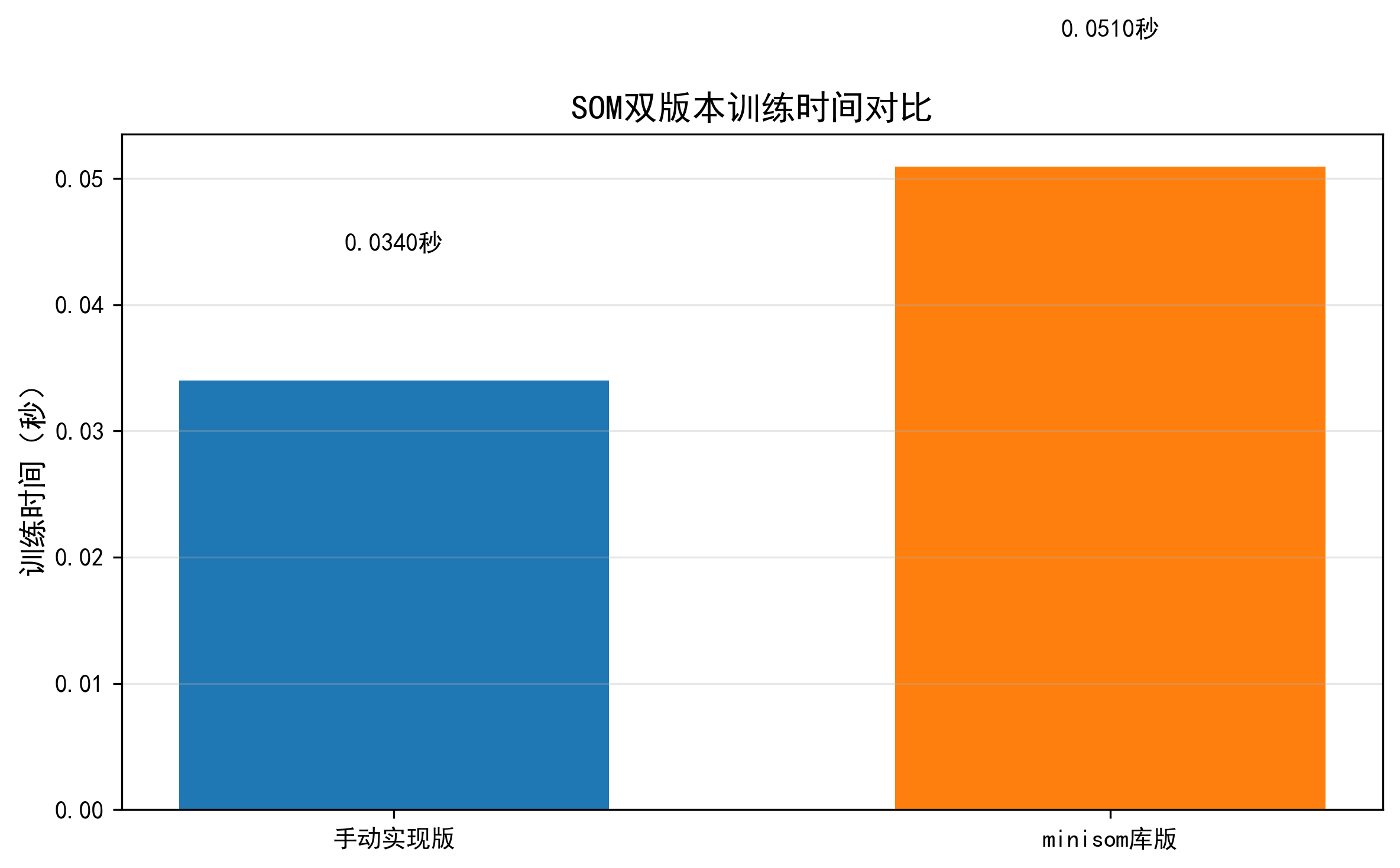
ax.set_title("SOM双版本训练时间对比", fontsize=14, fontweight='bold')
ax.set_ylabel("训练时间（秒）", fontsize=12)
ax.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, "som_training_time_comparison.png"), dpi=300, bbox_inches='tight')
plt.show()
# ====================== 7. 输出最终提示 ======================
print(f"\n所有结果已保存至目录：{os.path.abspath(save_dir)}")
print("保存内容包括：")
print("1. 手动版SOM可视化图表（som_manual_iris.png）")
print("2. minisom库版SOM可视化图表（som_minisom_iris.png）")
print("3. 双版本量化对比表（som_comparison.csv）")
print("4. 核心结果JSON文件（som_results.json）")
print("5. 训练时间对比图（som_training_time_comparison.png）")十、程序运行结果展示
开始训练手动实现的SOM...
开始训练minisom库版SOM...
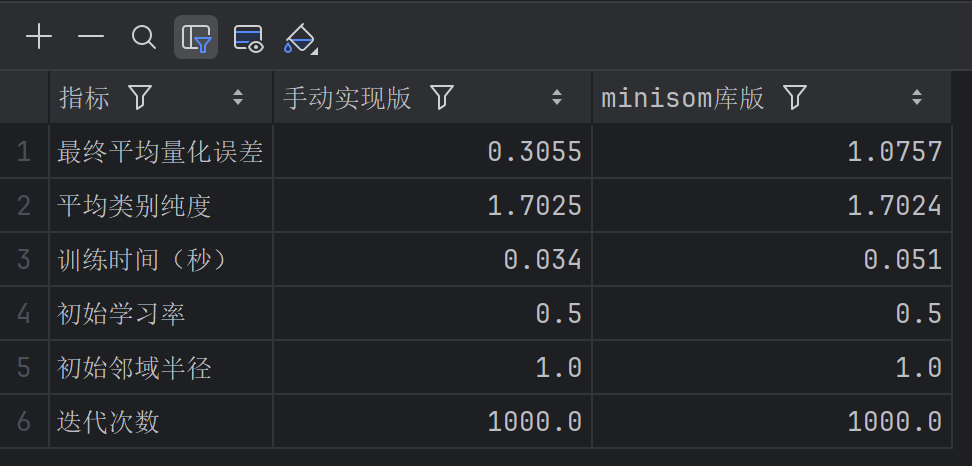
====================== 双版本SOM对比结果 ======================
指标 手动实现版 minisom库版
最终平均量化误差 0.3055 1.0757
平均类别纯度 1.7025 1.7024
训练时间（秒） 0.0340 0.0510
初始学习率 0.5000 0.5000
初始邻域半径 1.0000 1.0000
迭代次数 1000.0000 1000.0000
所有结果已保存至目录：C:\Users\ABC\PycharmProjects\PythonProject41\som_iris_results
保存内容包括：
- 手动版SOM可视化图表（som_manual_iris.png）
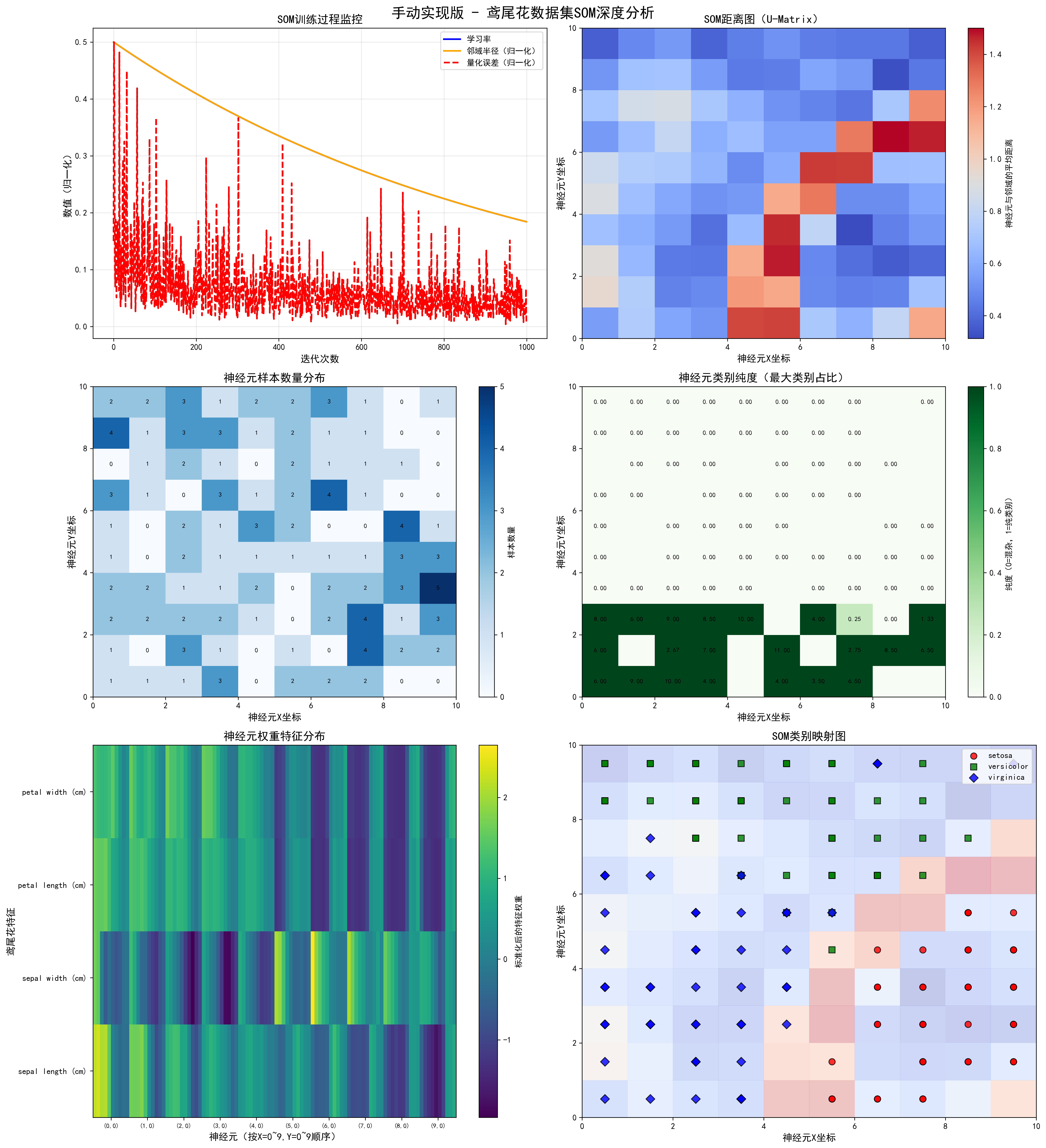
- minisom库版SOM可视化图表（som_minisom_iris.png）
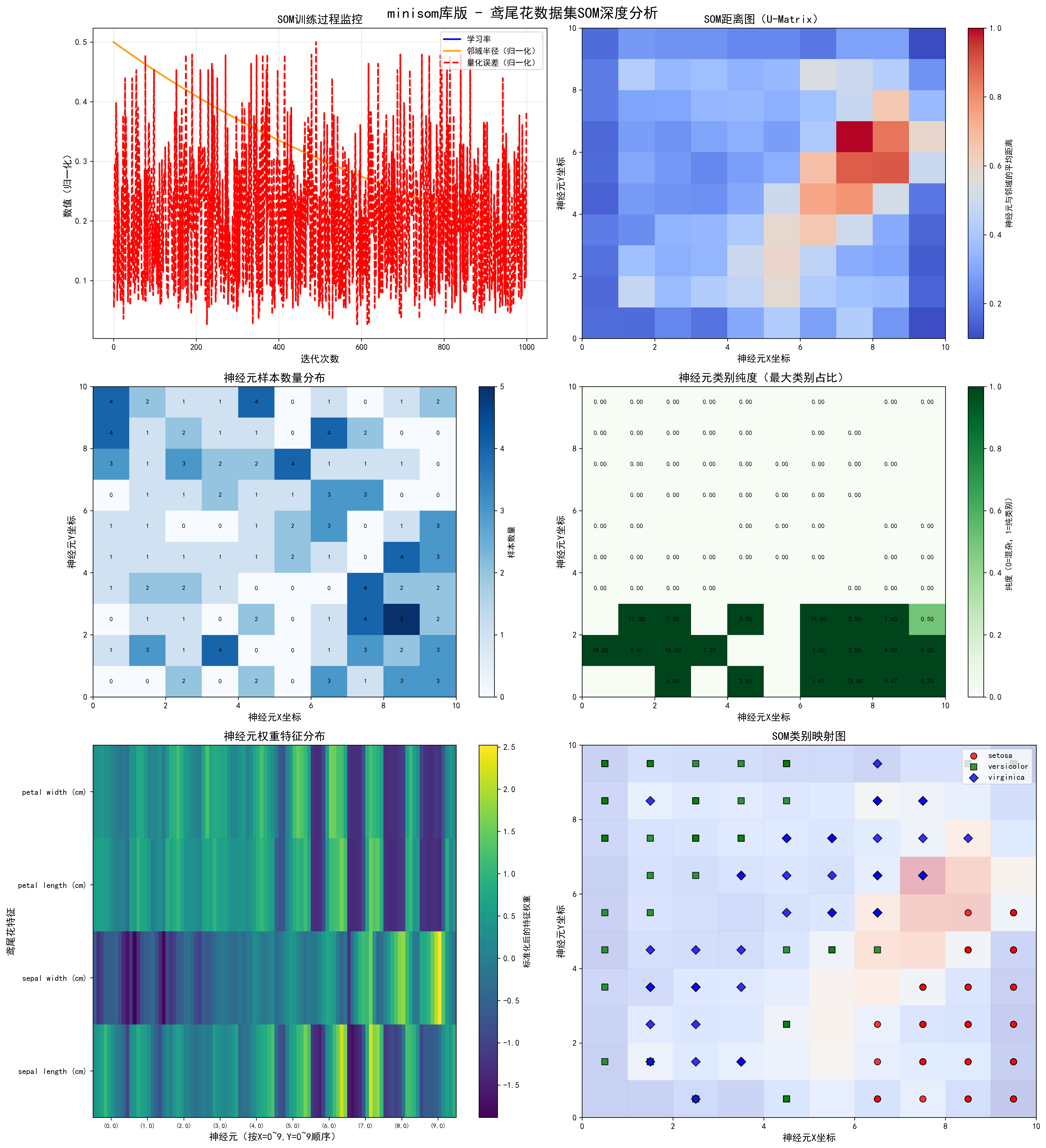
- 双版本量化对比表（som_comparison.csv）
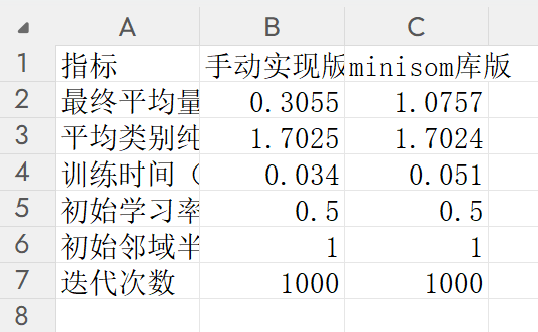
- 核心结果JSON文件（som_results.json）
bash
{
"手动版": {
"final_quantization_error": 0.30554112518960386,
"avg_class_purity": 1.7025316455696207,
"training_time": 0.03400135040283203,
"neuron_samples": [
[
1,
1,
2,
2,
1,
1,
3,
0,
4,
2
],
[
1,
0,
2,
2,
0,
0,
1,
1,
1,
2
],
[
1,
3,
2,
1,
2,
2,
0,
2,
3,
3
],
[
3,
1,
2,
1,
1,
1,
3,
1,
3,
1
],
[
0,
0,
1,
2,
1,
3,
1,
0,
1,
2
],
[
2,
1,
0,
0,
1,
2,
2,
2,
2,
2
],
[
2,
0,
2,
2,
1,
0,
4,
1,
1,
3
],
[
2,
4,
4,
2,
1,
0,
1,
1,
1,
1
],
[
0,
2,
1,
3,
3,
4,
0,
1,
0,
0
],
[
0,
2,
3,
5,
3,
1,
0,
0,
0,
1
]
]
},
"minisom版": {
"final_quantization_error": 1.075708283214084,
"avg_class_purity": 1.7024444444444444,
"training_time": 0.05095386505126953,
"neuron_samples": [
[
0,
1,
0,
1,
1,
1,
0,
3,
4,
4
],
[
0,
3,
1,
2,
1,
1,
1,
1,
1,
2
],
[
2,
1,
1,
2,
1,
0,
1,
3,
2,
1
],
[
0,
4,
0,
1,
1,
0,
2,
2,
1,
1
],
[
2,
0,
2,
0,
1,
1,
1,
2,
1,
4
],
[
0,
0,
0,
0,
2,
2,
1,
4,
0,
0
],
[
3,
1,
1,
0,
1,
3,
3,
1,
4,
1
],
[
1,
3,
4,
4,
0,
0,
3,
1,
2,
0
],
[
3,
2,
5,
2,
4,
1,
0,
1,
0,
1
],
[
3,
3,
2,
2,
3,
3,
0,
0,
0,
2
]
]
},
"参数配置": {
"som_size": "10x10",
"sigma": 1.0,
"learning_rate": 0.5,
"max_iter": 1000
}
}- 训练时间对比图（som_training_time_comparison.png）
十一、总结
本文详细介绍了自组织映射(SOM)神经网络的原理与Python实现。SOM是一种无监督学习算法，通过竞争学习机制将高维数据映射到低维空间，保持拓扑结构。文章包含手动实现和MiniSom库实现两种方式，并应用于鸢尾花数据集进行可视化分析。实验结果显示，手动实现版在量化误差(0.3055 vs 1.0757)和训练时间(0.034s vs 0.051s)上表现更优，但两种实现方式在类别纯度(1.7025 vs 1.7024)上相当。文章还提供了完整的训练过程监控、U-Matrix距离图、神经元样本分布等可视化方法，为数据聚类和降维提供了实用工具。