一、从复数:二维旋转的 "工具"
先复习复数的核心作用 ------表示平面旋转:
- 复数形式:z=a+bi(a,b 是实数,i^2=−1)
- 几何意义:复数对应平面向量 (a,b);

二、四元数:复数的 "三维扩展"
复数只能处理二维旋转,要解决三维问题,就需要增加两个虚部单位------ 这就是四元数。
1. 四元数的定义
四元数的一般形式:
q=w+xi+yj+zk
其中:
- w:实部(对应 "旋转的幅度");
- x,y,z:虚部系数;
- i,j,k:虚部单位,满足规则:i2=j2=k2=ijk=−1
且反对易:ij=k,ji=−k;jk=i,kj=−i;ki=j,ik=−j(旋转顺序会影响结果)
2. 四元数的两种写法
常把四元数拆成 "实部 + 向量":
- 形式 1:q=(w,v),其中 v=(x,y,z)(向量);
- 形式 2:纯虚四元数:若 w=0,则 q=v=xi+yj+zk(可直接对应三维向量)。
三、四元数的核心用途:三维旋转
复数能转二维,四元数能转三维 ------ 但旋转规则更 "特殊"。
1. 旋转的前提:旋转轴 + 旋转角
要让三维向量 p 旋转,需要先确定:
- 旋转轴:单位向量 u=(ux,uy,uz)(非单位需先归一化);
- 旋转角:θ(右手定则:大拇指沿旋转轴正向,四指是旋转方向)。
2. 构造 "旋转四元数"
根据旋转轴和角度,构造专门用来旋转的四元数:
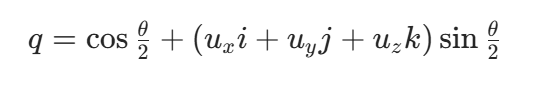
3. 执行旋转:"三明治乘法"
要旋转向量 p,步骤是:
- 把 p 写成纯虚四元数:
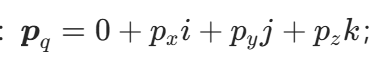
2.求旋转四元数的共轭:
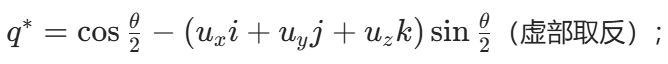
3.做 "三明治乘法":
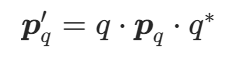
4.结果是纯虚四元数,它的虚部就是旋转后的向量。

四、举个例子:绕 Z 轴转 90°


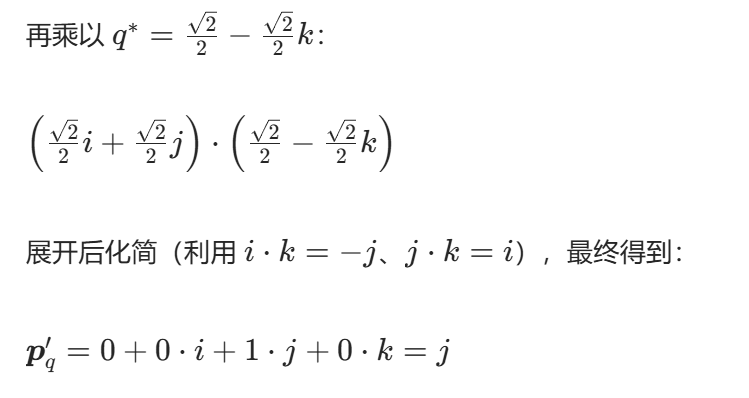
结果
旋转后的向量是 (0,1,0)(Y 轴正向),和预期一致!

五、轴
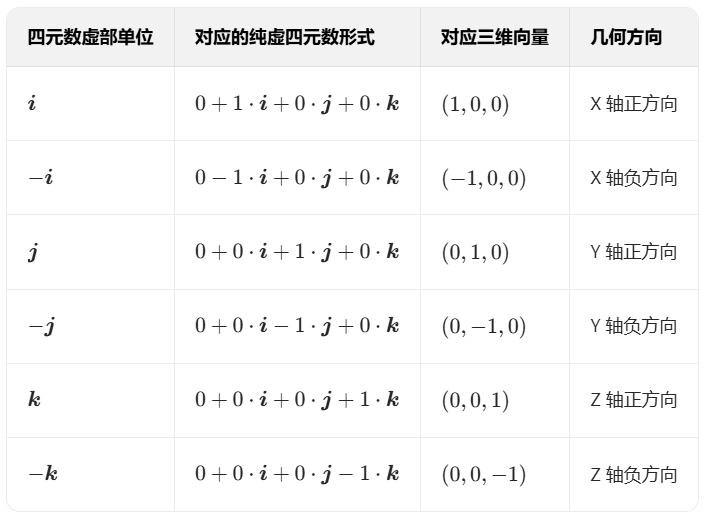
六、四元数的优点(对比旋转矩阵)
- 更高效:表示旋转只需 4 个数(旋转矩阵要 9 个);
- 无万向锁:矩阵旋转在某些角度会 "卡住",四元数不会;
- 插值方便:四元数可以平滑过渡两个旋转状态。