**郑重声明:**本文所涉安全技术仅限用于合法研究与学习目的,严禁任何形式的非法利用。因不当使用所导致的一切法律与经济责任,本人概不负责。任何形式的转载均须明确标注原文出处,且不得用于商业目的。
🔋 点赞 | 能量注入 ❤️ 关注 | 信号锁定 🔔 收藏 | 数据归档 ⭐️ 评论| 保持连接💬
🌌 立即前往 👉晖度丨安全视界🚀

▶ 信息收集
▶ 漏洞检测
▶ 初始立足点 ➢ 密码攻击 ➢ 密码破解理论(上)🔥🔥🔥▶ 权限提升
▶ 横向移动
▶ 报告/分析
▶ 教训/修复
目录
[1.1 加密、哈希和破解](#1.1 加密、哈希和破解)
[1.1.1 加密与哈希的对比](#1.1.1 加密与哈希的对比)
[1.1.2 密码哈希原理](#1.1.2 密码哈希原理)
[1.1.2.1 密码哈希原理](#1.1.2.1 密码哈希原理)
[1.1.2.2 哈希密码破解的本质](#1.1.2.2 哈希密码破解的本质)
[1.1.3 密码破解基础知识](#1.1.3 密码破解基础知识)
[1.1.3.1 密码破解示例:SHA-256哈希比对](#1.1.3.1 密码破解示例:SHA-256哈希比对)
[1.1.3.2 主流密码破解工具对比](#1.1.3.2 主流密码破解工具对比)
[1.1.3.3 GPU vs. CPU 在密码破解中的对比](#1.1.3.3 GPU vs. CPU 在密码破解中的对比)
[1.1.3.4 密码破解时间计算](#1.1.3.4 密码破解时间计算)
[②CPU+GPU模式 示例](#②CPU+GPU模式 示例)
[1.1.3.5 关键结论与影响因素](#1.1.3.5 关键结论与影响因素)
[欢迎❤️ 点赞 | 🔔 关注 | ⭐️ 收藏 | 💬 评论](#欢迎❤️ 点赞 | 🔔 关注 | ⭐️ 收藏 | 💬 评论)
1.密码破解理论
1.1 加密、哈希和破解
1.1.1 加密与哈希的对比
| 特性 | 加密 (Encryption) | 哈希 (Hashing) |
|---|---|---|
| 功能 | 双向:可加密也可解密 | 单向:只能生成,理论上不可逆 |
| 目的 | 保护数据机密性(传输或存储) | 验证数据完整性 或凭证(密码) |
| 密钥 | 对称加密 :同一个密钥 非对称加密:公钥加密,私钥解密 | 无需密钥(指密码哈希函数) |
| 输出 | 密文 (Ciphertext) | 哈希值/摘要 (Hash/Digest) |
| 典型算法 | AES (对称), RSA (非对称) | MD5, SHA1, SHA256 |
| 形象比喻 | 上锁的箱子,有钥匙才能开 | 指纹 或数字指纹,唯一代表原始数据 |
1.1.2 密码哈希原理
1.1.2.1 密码哈希原理
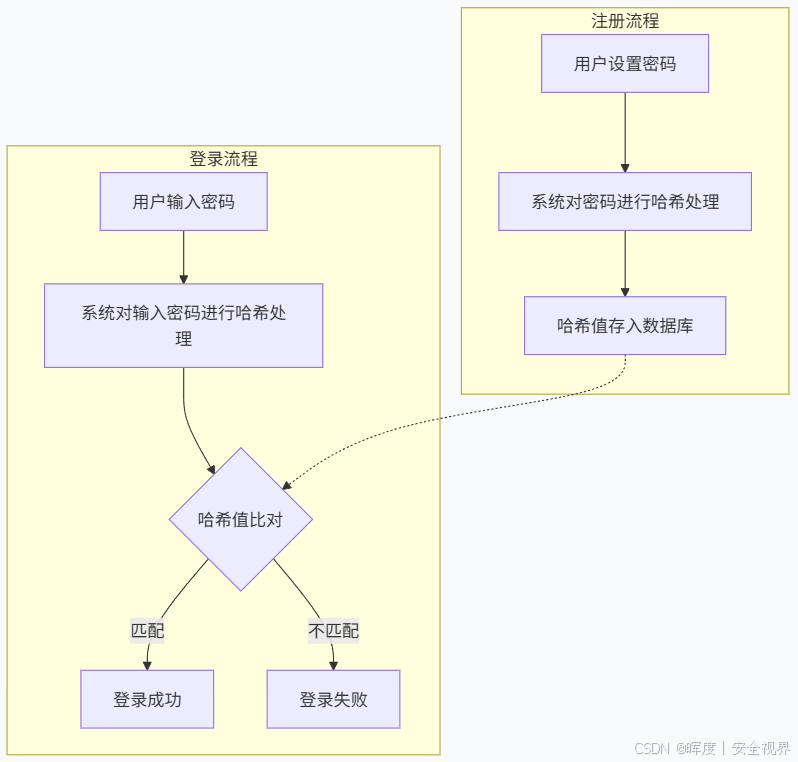
流程图说明:
-
注册流程 :用户设置密码 → 系统进行哈希处理 → 仅存储哈希值 至数据库。
-
登录流程 :用户输入密码 → 系统进行哈希处理 →与数据库中的哈希值进行比对 → 根据匹配结果决定登录成功或失败。
-
关键安全设计:数据库仅存储密码的哈希值(而非明文),登录验证通过比对哈希值完成,有效保护原始密码。
1.1.2.2 哈希密码破解的本质
-
目标:从获取到的哈希值反推出原始密码。
-
方法 :并非"解密",而是通过海量猜测与计算 ,寻找能生成++相同哈希值的明文++。
尝试明文1 → 哈希运算 → 与目标哈希比对 → ❌ 不匹配 尝试明文2 → 哈希运算 → 与目标哈希比对 → ❌ 不匹配 ... 尝试明文N → 哈希运算 → 与目标哈希比对 → ✅ 匹配 → **破解成功** -
攻击统称 :这类尝试性攻击统称为 "密码破解"。
⏳ 渗透测试中的策略:
由于破解过程可能非常耗时(取决于密码强度、算法与算力),在渗透测试中通常会:
-
作为并行任务在后台运行。
-
结合字典、规则、暴力破解等多种技术提高效率。
-
利用GPU加速工具(如Hashcat)来缩短时间。
💡 核心要点:
-
哈希是单向的,系统通过比对哈希值而非明文密码来验证用户。
-
密码破解是一场"猜测竞赛",其成功率与时间成本取决于密码复杂度和攻击者的算力资源。
-
安全建议 :使用强密码 、并采用加盐(Salt) 的哈希存储方式,能极大增加破解难度。
1.1.3 密码破解基础知识
与之前两篇文章中针对网络服务 和HTTP登录表单等 的在线基本字典攻击不同,密码破解可以节省网络带宽,不会锁定账户,并且不受传统防御技术的影响,对比如下:
| 特性 | 离线密码破解 | 在线字典攻击 |
|---|---|---|
| 环境 | 本地,无需网络交互 | 需向目标服务发起网络请求 |
| 带宽影响 | 无网络带宽消耗 | 可能受网络延迟、带宽限制 |
| 账户锁定风险 | 不会触发账户锁定 | 可能因多次失败尝试触发锁定机制 |
| 防御规避 | 不受登录失败锁定、验证码等防护影响 | 易受到常见登录防护措施阻断 |
核心优势 :离线破解是先把密码哈希获取到,然后在本地进行破解出密码明文后再进行登录,规避了网络层面的防护与限制。
1.1.3.1 密码破解示例:SHA-256哈希比对
假设获得SHA-256密码哈希值: 5b11618c2e44027877d0cd0921ed166b9f176f50587fc91e7534dd2946db77d6
破解过程(使用sha256sum):
-
尝试明文 "secret"
bashecho -n "secret" | sha256sum # 输出:2bb80d537b1da3e38bd30361aa855686bde0eacd7162fef6a25fe97bf527a25b # ❌ 与目标哈希不匹配 -
再次尝试明文 "secret"(验证一致性)
bashecho -n "secret" | sha256sum # 输出:2bb80d537b1da3e38bd30361aa855686bde0eacd7162fef6a25fe97bf527a25b # ✅ 哈希结果与第一次**完全相同**关键点:
1.相同输入永远产生相同哈希,这是哈希算法的确定性特性。
**2.-n:**由于echo输出的结果最后默认带换行符。-n是告诉echo不要将换行符包含在输出中。因为多了一个隐含的换行符,输出的hash值不一样。如下图:
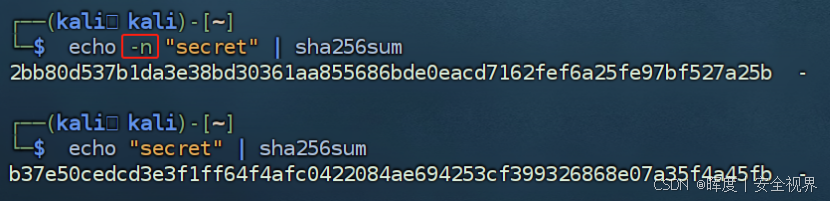
-
尝试明文 "secret1"
bashecho -n "secret1" | sha256sum # 输出:5b11618c2e44027877d0cd0921ed166b9f176f50587fc91e7534dd2946db77d6 # ✅ 与目标哈希**完全匹配**!
结论 :目标哈希对应的明文密码是 **"secret1"。**即,可用secret1作为登录密码进行登录。
💡 核心要点:
-
破解本质 :通过本地计算,不断猜测并哈希不同明文,直至找到与目标哈希匹配的结果。
-
哈希特性:
-
确定性:相同输入 ⇒ 相同输出。
-
雪崩效应 :输入微小变化(如
secret→secret1)⇒ 输出哈希截然不同。
-
-
技术细节 :使用
echo -n确保不包含换行符,避免因额外字符影响哈希结果。 -
工具与场景 :本例使用
sha256sum命令行工具演示,实际攻击中常使用 Hashcat 、John the Ripper 等专用工具进行大规模高效破解。
1.1.3.2 主流密码破解工具对比
| 特性 | John the Ripper (JtR) | Hashcat |
|---|---|---|
| 主要设计架构 | CPU优先的多功能破解工具 | GPU优先的高性能破解工具 |
| 硬件依赖 | 标准CPU即可运行,无需特殊驱动 | 需GPU支持以获得最佳性能 |
| GPU支持 | 支持(通过扩展),非原生设计 | 原生支持,专为GPU加速设计 |
| 所需计算框架 | 无特殊要求(仅CPU时) | 需OpenCL (开放计算语言)或CUDA(英伟达的并行计算平台)框架以调用GPU |
| 性能特点 | CPU性能稳定,GPU加速可选 | GPU破解速度通常远高于CPU |
| 易用性 | 配置相对简单,入门门槛较低 | 需正确配置GPU环境,初期设置稍复杂 |
| 适用场景 | 通用破解任务,尤其是CPU环境 | 大规模哈希破解,追求极致速度 |
📊 核心对比总结:
⚙️ 技术架构差异
-
JtR :传统CPU工具起家,后加入GPU支持,更像"多功能瑞士军刀"。
-
Hashcat :专为GPU并行计算设计,是"专业动力锤",擅长批量高速破解。
🚀 性能选择指南
-
选择JtR:你只有CPU资源、需要快速测试简单密码、或处理特殊格式(如加密文件)。
-
选择Hashcat:你拥有性能GPU(NVIDIA/AMD)、需要进行大规模暴力破解、或追求极限破解速度。
1.1.3.3 GPU vs. CPU 在密码破解中的对比
| 对比维度 | GPU(图形处理器) | CPU(中央处理器) |
|---|---|---|
| 核心数量 | 成千上万个小型核心 | 通常几个至几十个核心 |
| 设计目标 | 并行处理 大量相似计算任务 | 串行/复杂逻辑处理与通用计算 |
| 密码破解速度 | 极快,适合大规模并行哈希计算 | 较慢,尤其在暴力破解时 |
| 能耗与效率 | 单位功耗下的计算吞吐量高 | 相对能效较低 |
| 适用算法类型 | 大多数快速哈希算法(如MD5、SHA系列) | 慢速、抗并行的哈希算法(如bcrypt) |
🚀 为什么GPU更快?
-
海量核心并行 :GPU拥有数千个计算核心,可同时尝试成千上万个密码候选值,实现"人海战术"。
-
为哈希计算优化 :密码哈希计算是高度重复且相互独立的运算,完美契合GPU的大规模并行架构。
-
CPU 像一位大学教授,能处理复杂、多样的任务,但一次只能专心做一两件事。
-
GPU 像成千上万名小学生 ,每人计算一个简单问题,但总体效率极高。
-
⏳ 为什么某些算法在CPU上反而有优势?
以 bcrypt 为代表的故意设计缓慢的哈希算法:
-
抗并行设计 :算法内部依赖串行处理(如多次循环),难以被GPU的大规模并行有效加速。
-
内存访问复杂 :某些算法需要频繁访问内存,而GPU的核心虽然多,但共享内存带宽有限,容易形成瓶颈。
-
结果 :对于这类算法,CPU的单核性能强、内存延迟低 的特点可能使其实际破解效率接近甚至超过GPU。
1.1.3.4 密码破解时间计算
🔢 核心计算模型: ++破解时间 = 总密钥空间 ÷ 哈希速率++
1.计算密钥空间
密钥空间 指一个密码可能存在的所有组合总数,由 字符集大小 和 密码长度 共同决定。
-
公式 :
总密钥空间 = (字符集大小) ^ (密码长度) -
示例(62位字符集,5位密码):
-
小写字母 (26) + 大写字母 (26) + 数字 (10) = 62种可能/字符
-
密码长度:5位
-
总密钥空间 = 62⁵ = 916,132,832 种可能组合
-
💡 快速计算 :可使用Python命令
62**5直接得出结果。
2.测量哈希速率
哈希速率指:硬件每秒能计算哈希的次数,是决定破解速度的关键。
| 硬件模式 | 测试方法 | 示例算法速率对比 (基于示例数据) |
|---|---|---|
| 纯CPU模式 | 运行 hashcat -b (基准模式) |
MD5: ~100 MH/s SHA-256: ~15 MH/s |
| CPU+GPU模式 | 在同一命令下,连接GPU自动测试 | MD5: ~15,000 MH/s SHA-256: ~1,200 MH/s |
①CPU模式示例
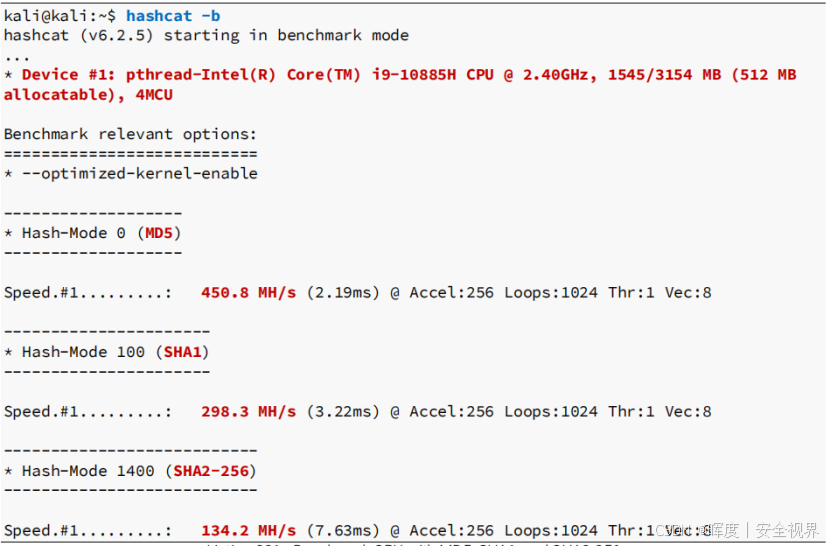
bash
$ hashcat -b| 参数 | 功能 | 使用场景示例 |
|---|---|---|
-b |
基准测试模式,测量当前硬件的哈希计算速度 | hashcat -b * 快速评估你的 CPU/GPU 性能,获得不同哈希算法的计算速度(哈希率)。 * 重要提示: * 在 Kali 虚拟机 中测试通常仅反映CPU性能(除非直通GPU)。 * 本地物理机 测试结果会因独立显卡性能大幅提升。 * 基准结果是估算破解时间的关键依据。 |
-m |
指定哈希类型(编号),告诉Hashcat要破解的哈希算法 | -m 0 (MD5) -m 1000 (NTLM) -m 1800 (sha512crypt) * 关键点 :必须正确指定目标哈希的算法编号,否则无法破解。 * 如何查编号 :运行 hashcat --help 可查看完整的哈希类型列表。 |
-a |
指定攻击模式,选择破解策略 | -a 0 字典攻击 :最常见的攻击,使用现成密码字典。 -a 3 暴力/掩码攻击:当对密码格式有了解时(如"大写+小写+数字+符号"),使用掩码可大幅缩小尝试范围。 a 6 组合攻击:将字典中的词条进行组合,尝试更多变体。 |
-o |
指定输出文件,保存破解成功的密码 | -o cracked_passwords.txt 将破解结果保存到文件,避免终端输出丢失。 |
⚠️ 注意 :实际速率因硬件型号、驱动、算法差异巨大,务必自行实测 。单位
MH/s= 百万次哈希/秒( 1,000,000个哈希每秒**)**。
②CPU+GPU模式 示例
下面使用一个附加了GPU的windows主机。同样,使用Hashcat -b的基准测试模式来计算MD5、SHA1和SHA-256的哈希速率。
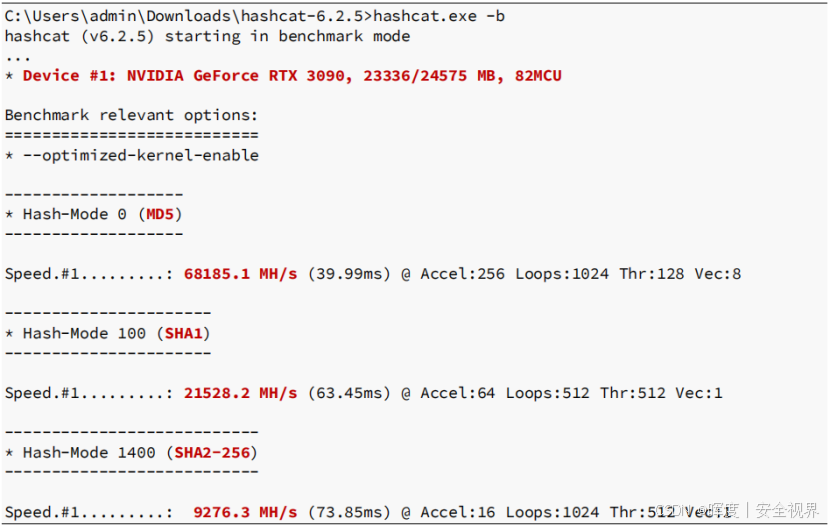
**综上,比较GPU和CPU的哈希率:**明显GPU要快很多。

3.计算实际破解时间(计算SHA256算法)
**计算SHA256算法,**将密钥空间与哈希速率代入公式,即可估算理论破解时间。

破解62字符集的5、8、10位数的SHA-256密码:
| 密码长度 | 总密钥空间 | CPU破解 (15 MH/s) | GPU破解 (1,200 MH/s) | 安全启示 |
|---|---|---|---|---|
| 5位 | 916,132,832 | ≈ 6.8秒 | < 1秒 | ❌ 极度脆弱 |
| 8位 | 62⁸ ≈ 2.18×10¹⁴ | ≈ 4.0小时 | ≈ 6.5小时 | ⚠️ 中等强度,GPU仍可破解 |
| 10位 | 62¹⁰ ≈ 8.39×10¹⁷ | ≈ 1.8年 | ≈ 2.8年 | ✅ 相对安全(但并非绝对) |

注意:
增加密码长度会以指数时间增加破解时间,而增加密码复杂性(字符集)只会以多项式时间增加破解时间。这意味着使用"++更长密码的密码策略++"比使用"更复杂密码的密码策略"更能抵御破解!!!
1.1.3.5 关键结论与影响因素
⚡ GPU的绝对速度优势
-
同一算法下,GPU破解速度可比CPU快数十至数百倍。
-
对于短密码/简单哈希 ,GPU可做到秒级或分钟级破解。
🛡️ 如何大幅增加破解时间(提升防御)
-
增加密码长度 :每增加1位,密钥空间呈指数级增长(如从8位到10位,时间从小时增至年)。
-
扩展字符集 :加入符号 (
!@#$%),使字符集从62增至90+,同样显著增大密钥空间。 -
使用慢哈希算法 :如 bcrypt、Argon2 ,其设计哈希速率极低 (可能仅每秒数千次),即使GPU也难加速,能将破解时间从年拉长至数百年。
⚠️ 现实因素提醒
-
以上为理论最长时间 (穷举所有组合)。实际攻击常使用字典、规则 ,可能极大缩短破解时间。
-
哈希加盐 能有效防御预计算攻击 (彩虹表),迫使攻击者必须针对每个盐值单独计算,增加成本。
核心要义 :密码破解是一场数学与时间的博弈 。通过理解密钥空间 与哈希速率的计算,可以量化评估密码的脆弱性,并指导设计更安全的密码存储策略。
欢迎❤️ 点赞 | 🔔 关注 | ⭐️ 收藏 | 💬 评论
每一份支持,都是我持续输出的光。

