0x3f 第23天 黑马web （前端三件套，maven，web入门、mysql）黑马反射注解 hot100普通数组

反射、注解、前端三件套、maven、web入门、mysql

1.缺失的第一个正数

核心思路，每个学生按学号坐好位置，肯定有一个人的位置是错的

最后检查一遍，谁的位置上做错了人，那个位置的数就是缺失的第一个正数

如果所有人位置都是对的，那就是n+1是缺失的m3？

影分身法：

判断每个人的位置和学号的方法就是if i == nums[i]-1

（-1是因为i是从0开始 nums[0]在i=0位置）

但是如果有两个nums[i]相等，比如1,1,2，那么会导致逻辑崩盘

因此我们引入了影分身法

具体就是将判断位置改成： if nums[i] == nums[nums[i]-1]

|----------------------------------|--------|-----------------|
| 条件 | 能否防死循环 | 核心问题 |
| i == nums[i]-1 | 不能 | 重复数字时会无限交换（死循环） |
| nums[i] == nums[nums[i]-1] | 能 | 重复数字时直接退出循环 |

综上：学号为nums[i]的人，应该坐在i+1的位置上

时间复杂度 n 空间复杂度1 因为是在原数组上修改

class Solution:
    def firstMissingPositive(self, nums: List[int]) -> int:
        n = len(nums)
        for i in range(n):
            while 1<=nums[i]<=n and nums[i] != nums[nums[i]-1]:
                #只处理学号合规的同学，并处理位置坐错的同学
                j = nums[i]-1
                #j是学号为nums[i]-1同学该坐的位置
                nums[i],nums[j] = nums[j],nums[i]
        for i in range(len(nums)):    
            if nums[i]!=i+1:
                return i+1
        return n+1

2.矩阵置零

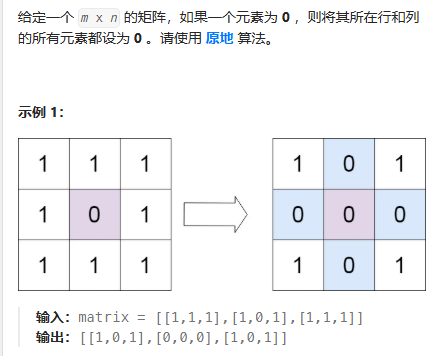
考虑把数据保存到 matrix 的第一行和第一列中。类似 Excel 表格的第一行和第一列，保存汇总信息。

核心思路：1.拿出两个布尔值：记录第一行，第一列是否有0

后续都是先处理1行1列之外的

2.拿第一行和第一列作为flag数组，出现0，就把对应的第一行和第一列置0

3.再遍历一遍，只要这行或这列出现0，元素全部变0

4.最后慢慢处理第一行第一列

first_row_has_zero、 first_col_has_zero

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m,n = len(matrix),len(matrix[0])
        first_row_has_zero = 0 in matrix[0]
        first_col_has_zero = any(row[0]==0 for row in matrix)

        for i in range(1,m):
            for j in range(1,n):
                if matrix[i][j]==0:
                    matrix[i][0] = 0
                    matrix[0][j] = 0
        for i in range(1,m):
            for j in range(1,n):
                if  matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j]=0
        if first_col_has_zero:
            for row in matrix:
                row[0] = 0
        if first_row_has_zero:
            for j in range (n):
                matrix[0][j] = 0