关于若干基础的几何问题

总结一下简单的关于点、线、圆之间的几何关系，涉及到向量、点积、叉积等之类的概念。由于很多需要公式表示，所以本文撰写起来稍显困难。

1、点与线的位置关系

问题

判断：

点 C 在向量 A B → 左侧 1. \text{点 } C \text{ 在向量 } \overrightarrow{AB} \text{ 左侧} 1.点 C 在向量 AB 左侧
点 C 在向量 A B → 右侧 2. \text{点 } C \text{ 在向量 } \overrightarrow{AB} \text{ 右侧} 2.点 C 在向量 AB 右侧

解决方法

如果 A B → × A C → > 0 \overrightarrow{AB}×\overrightarrow{AC}>0 AB ×AC >0，说明点 C 在向量 A B → 左侧 \text{点 } C \text{ 在向量 } \overrightarrow{AB} \text{ 左侧} 点 C 在向量 AB 左侧

如果 A B → × A C → < 0 \overrightarrow{AB}×\overrightarrow{AC}<0 AB ×AC <0，说明点 C 在向量 A B → 右侧 \text{点 } C \text{ 在向量 } \overrightarrow{AB} \text{右侧} 点 C 在向量 AB 右侧

这个时候涉及到叉积运算" × × ×"，下面简单说明一下

∗ ^* ∗叉积运算

首先，叉积运算是有方向的，故 a × b a×b a×b和 b × a b×a b×a的结果是不一样的

对于二维叉积：

设 A ( x a , y a ) A(x_a,y_a) A(xa,ya)， B ( x b , y b ) B(x_b,y_b) B(xb,yb)， C ( x c , y c ) C(x_c,y_c) C(xc,yc)

则 A B → \overrightarrow{AB} AB = ( x b − x a , y b − y a ) (x_b-x_a,y_b-y_a) (xb−xa,yb−ya)， A C → \overrightarrow{AC} AC = ( x c − x a , y c − y a ) (x_c-x_a,y_c-y_a) (xc−xa,yc−ya)

A B → × A C → = ( x b − x a ) ( y c − y a ) − ( y b − y a ) ( x c − x a ) \overrightarrow{AB}×\overrightarrow{AC}=(x_b-x_a)(y_c-y_a)-(y_b-y_a)(x_c-x_a) AB ×AC =(xb−xa)(yc−ya)−(yb−ya)(xc−xa)

对于三维叉积：
对于三维向量 a ⃗ = ( a 1 , a 2 , a 3 ) , b ⃗ = ( b 1 , b 2 , b 3 ) , 叉积的行列式表示为： \text{对于三维向量 } \vec{a} = (a_1, a_2, a_3),\; \vec{b} = (b_1, b_2, b_3),\; \text{叉积的行列式表示为：} 对于三维向量 a =(a1,a2,a3),b =(b1,b2,b3),叉积的行列式表示为：

a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ a 1 a 2 a 3 b 1 b 2 b 3 ∣ = ( a 2 b 3 − a 3 b 2 , − ( a 1 b 3 − a 3 b 1 ) , a 1 b 2 − a 2 b 1 ) \vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} =(a_2b_3-a_3b_2,-(a_1b_3-a_3b_1),a_1b_2-a_2b_1) a ×b = i a1b1j a2b2k a3b3 =(a2b3−a3b2,−(a1b3−a3b1),a1b2−a2b1)

2、点线最近距离

问题

【模板】点线最近距离_牛客网

1.点-直线最近点：输出点 C ( x c , y c ) C(x_c,y_c) C(xc,yc)到直线 A B AB AB的最近点

2.点-直线最近距离：输出点 C C C到直线 A B AB AB 的最近距离

解决方法

设有两个基础向量 A B → \overrightarrow{AB} AB ， A C → \overrightarrow{AC} AC , 用这个图看一下：

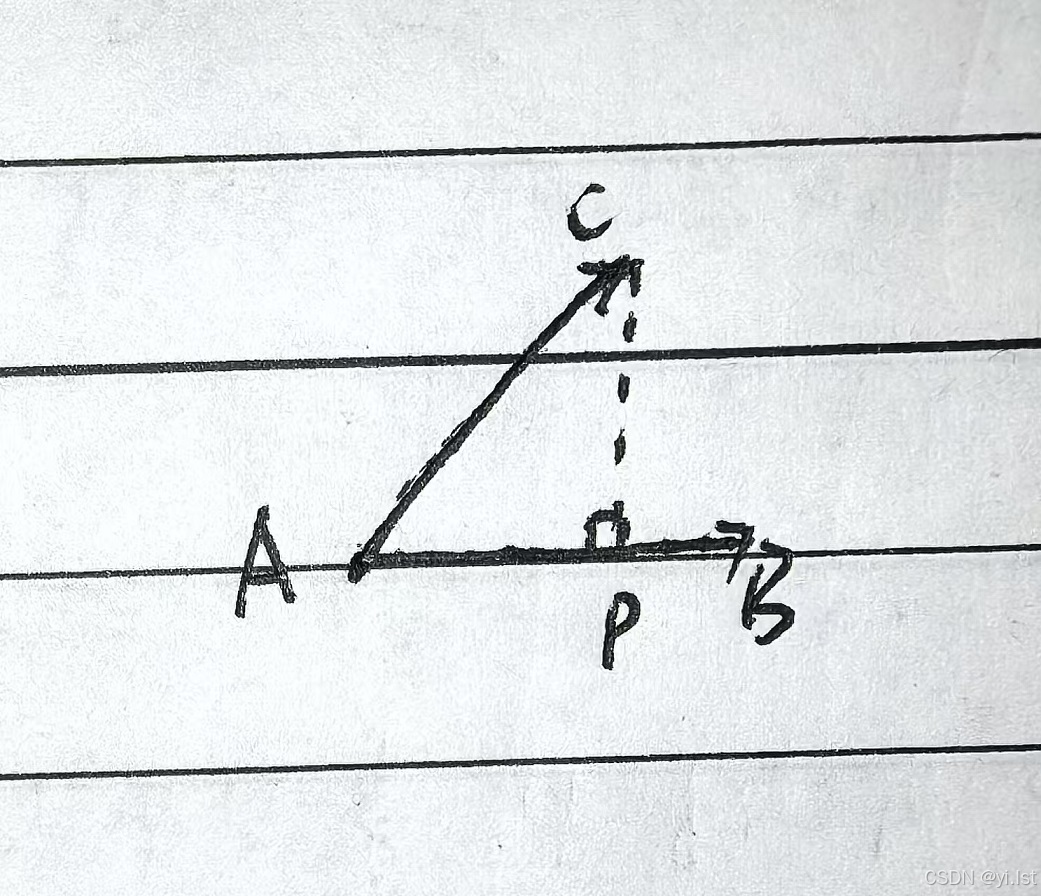
点到直线/线段核心公式

1. 基础向量定义

A B → = ( x B − x A , y B − y A ) , A C → = ( x C − x A , y C − y A ) \overrightarrow{AB} = (x_B - x_A,\ y_B - y_A),\quad \overrightarrow{AC} = (x_C - x_A,\ y_C - y_A) AB =(xB−xA, yB−yA),AC =(xC−xA, yC−yA)

2. 投影比例（核心）

t = A C → ⋅ A B → ∣ A B → ∣ 2 = ( x C − x A ) ( x B − x A ) + ( y C − y A ) ( y B − y A ) ( x B − x A ) 2 + ( y B − y A ) 2 t = \frac{\overrightarrow{AC} \cdot \overrightarrow{AB}}{|\overrightarrow{AB}|^2} = \frac{(x_C-x_A)(x_B-x_A) + (y_C-y_A)(y_B-y_A)}{(x_B-x_A)^2 + (y_B-y_A)^2} t=∣AB ∣2AC ⋅AB =(xB−xA)2+(yB−yA)2(xC−xA)(xB−xA)+(yC−yA)(yB−yA)

3. 线段场景的投影修正

t ′ = max ⁡ ( 0 , min ⁡ ( 1 , t ) ) t' = \max\left(0,\ \min\left(1,\ t\right)\right) t′=max(0, min(1, t))

4. 最近点 P 坐标

P = ( x A + t ′ ⋅ ( x B − x A ) , y A + t ′ ⋅ ( y B − y A ) ) P = \left(x_A + t' \cdot (x_B-x_A),\ y_A + t' \cdot (y_B-y_A)\right) P=(xA+t′⋅(xB−xA), yA+t′⋅(yB−yA))

5. 点到直线的距离

距离直线 = ∣ ( x B − x A ) ( y C − y A ) − ( y B − y A ) ( x C − x A ) ∣ ( x B − x A ) 2 + ( y B − y A ) 2 \text{距离直线} = \frac{|(x_B-x_A)(y_C-y_A) - (y_B-y_A)(x_C-x_A)|}{\sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}} 距离直线=(xB−xA)2+(yB−yA)2 ∣(xB−xA)(yC−yA)−(yB−yA)(xC−xA)∣

6. 点到线段的距离

距离线段 = ( x P − x C ) 2 + ( y P − y C ) 2 \text{距离线段} = \sqrt{(x_P - x_C)^2 + (y_P - y_C)^2} 距离线段=(xP−xC)2+(yP−yC)2

点到圆的切点问题

问题

【模板】点圆位置关系_牛客网

判断：

点与圆的位置关系
如果点在圆的外面，求点到圆的两个切点

位置关系判断：

计算点 A 到圆心 O 的距离平方 d i s t = ( x A − x O ) 2 + ( y A − y O ) 2 dist=(x_A−x_O)^2+(y_A−y_O)^2 dist=(xA−xO)2+(yA−yO)2，与半径平方 r 2 r^2 r2比较：

若 d i s t < r 2 dist<r2 dist<r2：点在圆内，输出 1；
若 d i s t = r 2 dist=r^2 dist=r2：点在圆上，输出 2；
若 d i s t > r 2 dist>r^2 dist>r2：点在圆外，计算并输出两个切点。

切点坐标推导：

设 O A = ( d x , d y ) = ( x A − x O , y A − y O ) OA=(dx,dy)=(x_A−x_O,y_A−y_O) OA=(dx,dy)=(xA−xO,yA−yO)，点 A 到圆心的距离为 d = d i s t d=dist d=dist。

利用几何关系（切点与圆心的连线垂直于切点与点 A 的连线），推导得切点公式：

k = r 2 dist k = \dfrac{r^2}{\text{dist}} k=distr2（向量 O A → \overrightarrow{OA} OA 向圆内缩放的比例）；
t = r ⋅ dist − r 2 dist t = \dfrac{r \cdot \sqrt{\text{dist} - r^2}}{\text{dist}} t=distr⋅dist−r2 （垂直方向的偏移比例）； -
切点 P 1 = ( x O + d x ⋅ k − d y ⋅ t , y O + d y ⋅ k + d x ⋅ t ) P_1 = \left(x_O + dx \cdot k - dy \cdot t,\ y_O + dy \cdot k + dx \cdot t\right) P1=(xO+dx⋅k−dy⋅t, yO+dy⋅k+dx⋅t)
- 切点 P 2 = ( x O + d x ⋅ k + d y ⋅ t , y O + d y ⋅ k − d x ⋅ t ) P_2 = \left(x_O + dx \cdot k + dy \cdot t,\ y_O + dy \cdot k - dx \cdot t\right) P2=(xO+dx⋅k+dy⋅t, yO+dy⋅k−dx⋅t)。

最开始看到这些题的时候都以为很简单，但其实都涉及到一些简单但没见过的计算几何的，这里一并总结。