Improving Time Series Forecasting via Instance-aware Post-hoc Revision
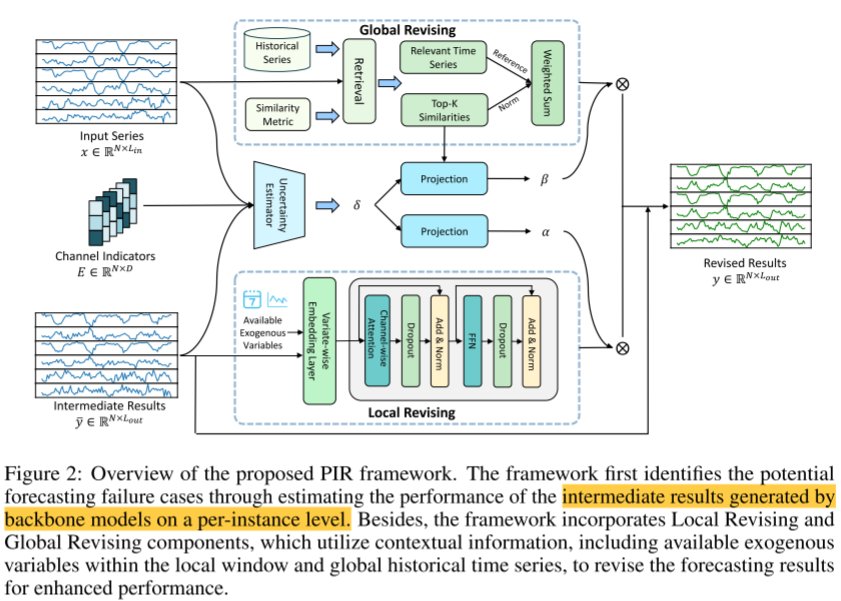
PIR框架
PIR框架 的整体思路是**后处理**,即**先用一个主干模型给出一个初始预测结果,然后再对这个结果进行修正**。
目的:为了修正这个错误,首先必须精准识别哪些预测是失败的。
本质 :作者将这个识别失败 的过程建模为一个"不确定性估计 "任务。(不确定这个预测是否有把握,需要给出置信度)
名词解释:
不确定性估计任务 的目标不仅是让模型给出预测结果,还要让模型告诉我们它对这个结果有多大把握 。在传统机器学习或深度学习任务中,模型通常给出一个点预测,比如"明天的气温是 25 度"。而**不确定性估计则要求模型输出一个范围或概率**,比如"明天的气温在 23 度到 27 度的概率是 95%",或者"我是瞎猜的,置信度很低"。
不确定性的两个主要来源:
① 数据不确定性:数据本身就是乱的、有噪声的,这是客观存在的,无法通过增加数据量来消除。(如:传感器故障导致的数据缺失、测量误差等)
② 模型不确定性 :模型因见识太少或能力不足 而感到困惑,这是主观的,可以通过增加更多训练数据来降低。(如:长尾分布)
Failure Identification: 如何找出预测结果中哪些样本是可靠的
PIR的解决方案 :以"误差"作为"不确定性"的代理 ,提出一种数据驱动方法:训练一个小型的神经网络 来**预测"预测误差本身"**。
具体实现 :设计两层的全连接神经网络fθf_\thetafθ用于估计不确定性σ\sigmaσ。
输入特征:
① 原始输入时间序列xxx
② 主干生成的初始预测结果y^\hat{y}y^
③ EEE: 通道嵌入矩阵,用于捕获不同变量(Channel)的特性。
输出特征:
δ\deltaδ:估计的确定性值
辅助函数:
由于无法直接获得"真实的不确定性" ,作者假设:预测误差越大,意味着不确定性越高。因此,模型被训练去预测MSE(均方误差)。
公式如下 :
Lue=1N∑1N∣∣δ−∣∣yˉ−y∣∣22∣∣1 \mathcal{L}{ue} = \frac{1}{N}\sum{1}^{N}||\delta - ||\bar{y} - y||{2}^{2}||{1} Lue=N11∑N∣∣δ−∣∣yˉ−y∣∣22∣∣1
- ∣∣yˉ−y∣∣22||\bar{y} - y||_{2}^{2}∣∣yˉ−y∣∣22 :这是真实的预测误差 (即初始预测 yˉ\bar{y}yˉ 与真实标签 yyy 之间的 MSE)。
- δ\deltaδ :这是网络估计的不确定性。
- ∣∣⋅∣∣1||\cdot||_{1}∣∣⋅∣∣1 :使用 MAE(L1 Loss)来让 δ\deltaδ 尽可能逼近真实的 MSE。
Failure Identification的作用:
通过这个模块,框架知道主干模型在当前样本上的表现大概率会产生多大的误差(δ\deltaδ), 如果 δ\deltaδ 很大(预测很不准),后续的 α\alphaα 和 β\betaβ 权重就会变大,模型就会更多地依赖 Local Revising 和 Global Revising 的结果来修正原始预测。
Local Revising: 局部修正
利用局部窗口内的上下文信息来增强预测准确性。
① 利用领先-滞后效应,时间序列数据中,协变量的变化往往领先于目标变量,比如:气温升高(协变量)可能导致几个小时后的用电量增加。因此,协变量的预测结果可以暗示未来趋势。
② 引入先验已知信息 ,有些信息是提前已知的,比如时间戳、节假日或天气预报。这些被称为外生变量。他们作为先验条件,可以帮助模型应对由自然规律引起的突发分布偏移。
③ 弥补通道独立策略的不足:很多模型选择通道独立的策略,将每个变量单独作为一条序列,忽略变量之间的关系,Local Revising模块重新引入变量间的关联。
具体实现:
嵌入与投影:
模型将协变量和先验信息映射为隐藏状态并拼接到一起H0=[hco,hexo]H_0 = [h_{co}, h_{exo}]H0=[hco,hexo] :
① 中间预测结果 (yˉ\bar{y}yˉ) :即主干模型输出的初步预测。通过一个可训练的线性投影层 CoVariateEmb 转化为协变量表示 hcoh_{co}hco 。
② 外生变量 (ccc) :如时间、文本描述等。通过 ExoVariateEmb 转化为外生变量表示 hexoh_{exo}hexo ,如果是数值特征就用线性层,如果是文本描述可以使用语言模型处理。
Transfomer处理与生成:
① 相关性提取 :将拼接后的 H0H_0H0 输入到一个标准的 Transformer 模块中。利用 Transformer 的 Attention 机制,模型可以显式地捕捉协变量(预测值)与外生变量(如时间、环境因素)之间的复杂关联 。
② 生成修正结果: 最后通过一个线性预测头(Linear prediction head)输出修正后的局部预测结果。
Global Revising: 全局修正
传统模型 通常在大多数常见样本上表现良好 ,但在遇到稀有或特殊的数值模式时容易失败 ,这些稀有样本构成了所谓的长尾分布 。既然模型没有学好稀有模式,不如直接检索历史数据库 ,看看以前发生类似情况时,后续走势如何,然后直接照搬或参考以前的走势。
构建检索数据库:
① 数据来源:只使用训练集的输入-输出对(XtrainX_{train}Xtrain,YtrainY_{train}Ytrain)构建数据库
检索相似序列**(Top-K Retrieval)**:
对于当前的输入序列 xxx,系统会在数据库中寻找最相似的 KKK 个历史序列:
编码(Encoding):使用Enc()函数对序列进行处理。
相似度计算 :使用余弦相似度计算输入xxx与数据库中序列的距离
结果:得到最相似的K个历史片段及其对应的未来真值YYY
生成全局修正结果:
核心假设 :相似的实例往往表现出相似的未来趋势 ,这意味着检索的历史真值本身就可以直接作为当前预测的参考。
加权求和: 系统不修改主干模型结构,而是对检索到的K个历史未来值进行加权平均。