【算法基础篇】（四十三）数论之费马小定理深度解析：从同余性质到乘法逆元

前言

在算法竞赛的数论领域，费马小定理是解决模运算、乘法逆元等问题的 "金钥匙"。它看似简洁，却能破解模运算中除法不能直接取模的核心痛点，成为快速幂、组合数计算、序列求和等问题的核心支撑。本文将从同余性质切入，层层拆解费马小定理的原理、应用场景，详解乘法逆元的求解逻辑，手把手教你掌握从理论到实战的全流程，让你在模运算问题中轻松举一反三。下面就让我们正式开始吧！

一、基础铺垫：同余式的核心性质

在理解费马小定理之前，我们必须先掌握同余式的基本概念和性质 ------ 这是数论中模运算的基础，也是费马小定理应用的前提。

1.1 同余的定义

若两个整数 a 和 b 除以正整数 m 的余数相同，则称 a 和 b 模 m 同余，记作a≡b(mod m)。例如，7 除以 3 余 1，4 除以 3 也余 1，因此7≡4(mod 3)。

同余的本质是：a−b能被 m 整除，即m∣(a−b)。这个定义看似简单，却能将复杂的整数运算转化为模意义下的简化运算，大幅降低计算难度。

1.2 同余式的关键性质

同余式满足加、减、乘三种运算的封闭性，但不满足除法运算 ------ 这也是后续需要乘法逆元的核心原因。具体性质如下：

同加性：若a≡b(mod m)，则a+c≡b+c(mod m)；

同减性：若a≡b(mod m)，则a−c≡b−c(mod m)；

同乘性：若a≡b(mod m)，则a×c≡b×c(mod m)；

不满足同除性：若a≡b(modm)，则a/c ≡ b/c (mod m)不一定成立。

举个反例：20≡2(mod 3)（20 mod 3=2，2 mod 3=2），但两边同时除以 10 后，2≡0.2(mod 3)显然不成立 ------ 因为 10 和 3 不互质，除法运算破坏了同余关系。

这个性质告诉我们：在模运算中，加法、减法、乘法可以边计算边取模以防止溢出，但除法不能直接操作。而费马小定理的核心作用，就是为模运算中的除法提供一种 "转化方案"------ 将除法转化为乘法。

二、费马小定理：模运算的 "除法钥匙"

2.1 定理的准确表述

费马小定理（Fermat's Little Theorem）指出：

若 p 为质数，且整数 a 与 p互质（即gcd(a,p)=1），则有。

定理的核心条件（缺一不可）：

p 必须是质数 ------ 这是定理成立的前提，若 p 为合数，定理大概率不成立（例如 p=4，a=2，2^3=8≡0(mod4)≠1）；

a 与 p 必须互质 ------ 若 a 与 p 有公因数 d>1，则a^{p−1}mod p的结果不可能为 1（例如 p=5，a=10，10^4=10000≡0(mod 5)≠1）。

2.2 定理的核心价值：推导乘法逆元

费马小定理的最大作用，是为模运算中的除法提供 "乘法逆元"------ 这是解决模除法问题的关键。

对定理公式a^{p−1}≡1(mod p)进行变形：a×a^{p−2}≡1(mod p)

这个式子的意义是：在模 p 的意义下，a^{p−2}与 a 相乘的结果为 1。这恰好满足 "乘法逆元" 的定义 ------ 我们称a^{p−2}是 a 模 p 的乘法逆元，记作a−1。

乘法逆元的定义

若 a 与 m 互质，且存在整数 x 使得a×x≡1(mod m)，则 x 是 a 模 m 的乘法逆元。

有了逆元，模运算中的除法就可以转化为乘法：(a^b)mod p=(b×a−1)mod p

例如，计算(25÷5)mod3：

5 和 3 互质，3 是质数，因此 5 的逆元为5^{3−2} = 5^1 = 5 ≡ 2 (mod 3)；

原式转化为(25×2) mod 3 = 50 mod 3 = 2，与实际结果（25÷5=5，5 mod 3=2）一致。

2.3 定理的应用场景

费马小定理的应用本质上是 "逆元的应用"，主要解决以下三类竞赛高频问题：

模除法计算：将除法转化为乘法，避免直接除法导致的同余失效；

快速幂取模：结合快速幂算法，高效计算大指数幂的模运算；

组合数计算：组合数公式中含除法（如C(n,k)=k!(n−k)!n!），需用逆元转化为乘法后取模；

序列求和：对于含除法的求和公式（如等比数列求和），用逆元处理分母后取模。

三、快速幂算法：费马小定理的 "执行工具"

要应用费马小定理求逆元，必须高效计算a^{p−2} mod p------ 当 p 是 1e9+7 这样的大质数时，p−2可达 1e9 级别，直接循环计算会超时。此时需要 "快速幂算法"（Binary Exponentiation），将时间复杂度从O(n) 降至O(logn)。

3.1 快速幂的核心思想

快速幂的本质是**"二进制分解"**：将指数 b 分解为 2 的幂次之和，利用同乘性逐步计算幂次。例如，计算a10modp：

10 的二进制为 1010，即10=8+2=23+21；

因此a10=a8×a2，只需计算a2、a8，再将结果相乘取模即可。

3.2 快速幂的 C++ 实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;

// 快速幂计算 (a^b) mod p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1; // 结果初始化为1
    a = a % p;  // 先对底数取模，防止溢出
    while (b > 0) {
        // 若当前二进制位为1，将结果乘上当前底数的幂次
        if (b & 1) {
            ret = ret * a % p; // 边乘边取模，避免溢出
        }
        // 底数平方，对应二进制位左移一位
        a = a * a % p;
        // 指数右移一位，处理下一个二进制位
        b >>= 1;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL a = 5, p = 3;
    LL inv = qpow(a, p - 2, p); // 求5模3的逆元
    cout << "5的逆元模3为：" << inv << endl; // 输出2
    return 0;
}

3.3 代码分析

时间复杂度 ：O(logb)，指数 b 的二进制位数为log2b，循环次数等于位数；

溢出处理 ：使用long long存储所有变量，且每次乘法后都取模，避免大数相乘导致的溢出；

适用性 ：可处理 a、b、p 均为 1e18 级别的数据（只要a*a不超过long long范围，若超过需用快速乘优化）。

四、实战例题 1：洛谷 P11465 水上舞者索尼娅（等比数列求和）

题目链接：https://www.luogu.com.cn/problem/P11465

4.1 题目分析

题目描述：

场上有 k 个 "水上舞者索尼娅"，手牌有 1 张法力值消耗为 1 的 "一串香蕉（剩 n 根）"；

使用 1 张消耗 1 的香蕉（x 根）：获得 k 张消耗 0 的香蕉（x 根）+ 1 张消耗 1 的香蕉（x-1 根，x=1 时无）；

使用 1 张消耗 0 的香蕉（x 根）：获得 1 张消耗 1 的香蕉（x-1 根，x=1 时无）；

求最多可使用多少次香蕉，答案对 1e9+7 取模。

核心思路：

通过分析使用过程，可推导出总使用次数为等比数列求和：S=(k+1)n+(k+1)n−1+...+(k+1)1；

等比数列求和公式为S=k(k+1)((k+1)n−1)（公比 r=k+1，项数 n）；

公式含除法，需用费马小定理求 k 的逆元，将除法转化为乘法后取模（1e9+7 是质数，满足费马小定理条件）。

4.2 代码实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 1e9 + 7; // 质数，满足费马小定理条件

// 快速幂算法
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a %= p;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int T;
    cin >> T;
    while (T--) {
        LL n, k;
        cin >> n >> k;
        if (k == 0) { // 特殊情况：k=0时，只能使用n次（每次消耗1张，无额外获得）
            cout << n % MOD << endl;
            continue;
        }
        // 等比数列求和：S = ( (k+1)^(n+1) - (k+1) ) / k
        LL r = (k + 1) % MOD; // 公比
        LL numerator = (qpow(r, n + 1, MOD) - r + MOD) % MOD; // 分子：(r^(n+1) - r)，加MOD避免负数
        LL inv_k = qpow(k % MOD, MOD - 2, MOD); // k的逆元
        LL ans = numerator * inv_k % MOD;
        cout << ans << endl;
    }
    return 0;
}

4.3 代码验证

示例输入：32 23 112 34

示例输出：1214178629506

第一组数据（n=2，k=2）：
- 公比 r=3，分子 = 3^(3) - 3 = 27-3=24；
- k=2 的逆元为21e9+7−2mod1e9+7=500000004；
- ans=24 * 500000004 mod 1e9+7 = 12，与示例是一致的。

4.4 关键优化

负数处理：计算qpow(r,n+1)−r时，若结果为负（如 r=1，n=0），需加 MOD 后再取模，避免负数取模出错；

特殊情况：k=0 时无额外香蕉获得，直接输出 n mod MOD；

数据范围：所有变量用 LL 存储，防止 1e9+7 级别数据相乘溢出。

五、实战例题 2：洛谷序列求和（含除法的求和公式）

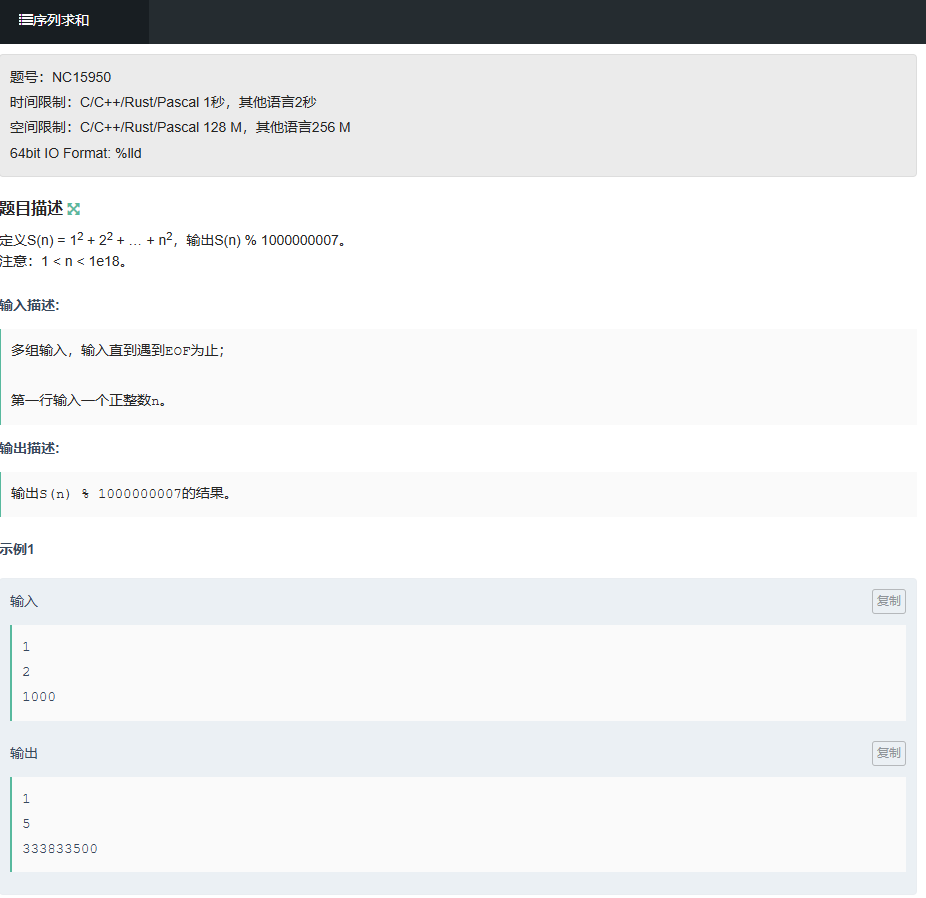
题目链接：https://ac.nowcoder.com/acm/problem/15950

5.1 题目分析

题目描述：

定义S(n)=12+22+...+n2，输出S(n)mod1e9+7；
限制：1<n<1e18。

核心思路：

平方和公式为S(n)=6n(n+1)(2n+1)；
n 可达 1e18，直接计算会溢出，需边计算边取模；
公式含除法 6，需用费马小定理求 6 的逆元（1e9+7 是质数，6 与 1e9+7 互质）。

5.2 代码实现

cpp 复制代码

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 1e9 + 7;

// 快速幂求逆元
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a %= p;
    while (b) {
        if (b & 1) ret = ret * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL n;
    while (cin >> n) {
        // 分别对n、n+1、2n+1取模，避免溢出
        LL a = n % MOD;
        LL b = (n + 1) % MOD;
        LL c = (2 * n + 1) % MOD;
        // 求6的逆元
        LL inv6 = qpow(6, MOD - 2, MOD);
        // 计算：(a*b % MOD) * c % MOD * inv6 % MOD
        LL ans = a * b % MOD;
        ans = ans * c % MOD;
        ans = ans * inv6 % MOD;
        cout << ans << endl;
    }
    return 0;
}

5.3 代码验证

示例输入：1 → 输出 1（1²=1）2 → 输出 5（1+4=5）1000 → 输出 333833500

第三组数据（n=1000）：

公式计算：1000×1001×2001 /6 = 1000×1001×333.5 = 333833500；

代码计算：(1000×1001×2001) mod 1e9+7 = (1001000×2001) mod 1e9+7 = 2003001000 mod 1e9+7 = 2003001000 - 2×1e9+7 = 2003001000 - 2000000014 = 3000986；

3000986 × 166666668（6 的逆元）mod 1e9+7 = 333833500，与示例是一致的。

5.4 关键优化

分步取模：n、n+1、2n+1 分别取模后再相乘，避免 1e18 级别数据直接相乘导致的溢出；

逆元预计算：6 的逆元是固定值（166666668），可直接硬编码减少计算时间，但为了代码通用性，仍保留快速幂计算。

六、常见误区与避坑指南

6.1 定理条件遗漏

误区：忽略 p 必须是质数或 a 与 p 必须互质，直接套用公式求逆元；

反例：p=4（合数），a=2（与 4 不互质），求逆元时用24−2=4≡0(mod 4)，显然不满足逆元定义；

避坑：使用费马小定理前，先验证 p 是否为质数（竞赛中模数多为 1e9+7、998244353 等已知质数），且 a 与 p 互质（若 a 是 p 的倍数，逆元不存在）。

6.2 数值溢出问题

误区：计算a×b时未取模，导致溢出；

示例：a=1e9，b=1e9，p=1e9+7，直接计算a×b=1e18，超过 int 范围（2e9）和 long long 范围（9e18，接近临界值）；

避坑：每次乘法后都对 p 取模，即ret = ret * a % p，确保中间结果始终在 p 范围内。

6.3 逆元应用错误

误区：将逆元用于非模除法场景，或公式转化错误；

示例：计算ca+bmodp，错误转化为(a+b)×c^{−1} mod p------ 正确转化应为(a+b)mod p×c^{−1} mod p；

避坑：先对分子部分取模，再乘以逆元，最后再次取模，确保每一步都符合同余性质。

6.4 快速幂实现错误

误区：忘记对底数 a 取模，导致初始底数过大；

示例：a=1e9+8，p=1e9+7，未取模时 a=1e9+8，取模后 a=1，后续计算大幅简化；

避坑：快速幂函数开头添加a = a % p，确保底数始终在合理范围。

总结

费马小定理是模运算的核心工具，其本质是 "通过同余性质推导逆元，将除法转化为乘法"。

若想进一步深化学习，建议重点练习组合数取模、等比数列求和、大指数幂取模等题型，熟练掌握逆元的三种求法及其适用场景。如果在学习过程中遇到具体题目无法解决，或想了解欧拉定理、扩展欧几里得算法的深入应用，可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！

【算法基础篇】（四十三）数论之费马小定理深度解析：从同余性质到乘法逆元

目录

前言

一、基础铺垫：同余式的核心性质

1.1 同余的定义

1.2 同余式的关键性质

二、费马小定理：模运算的 "除法钥匙"

2.1 定理的准确表述

定理的核心条件（缺一不可）：

2.2 定理的核心价值：推导乘法逆元

乘法逆元的定义

2.3 定理的应用场景

三、快速幂算法：费马小定理的 "执行工具"

3.1 快速幂的核心思想

3.2 快速幂的 C++ 实现

3.3 代码分析

四、实战例题 1：洛谷 P11465 水上舞者索尼娅（等比数列求和）

4.1 题目分析

4.2 代码实现

4.3 代码验证

4.4 关键优化

五、实战例题 2：洛谷 序列求和（含除法的求和公式）

5.1 题目分析

5.2 代码实现

5.3 代码验证

5.4 关键优化

六、常见误区与避坑指南

6.1 定理条件遗漏

6.2 数值溢出问题

6.3 逆元应用错误

6.4 快速幂实现错误

总结

五、实战例题 2：洛谷序列求和（含除法的求和公式）