Timer-XL: Long-Context Transformers For Unified Time Series Forecasting
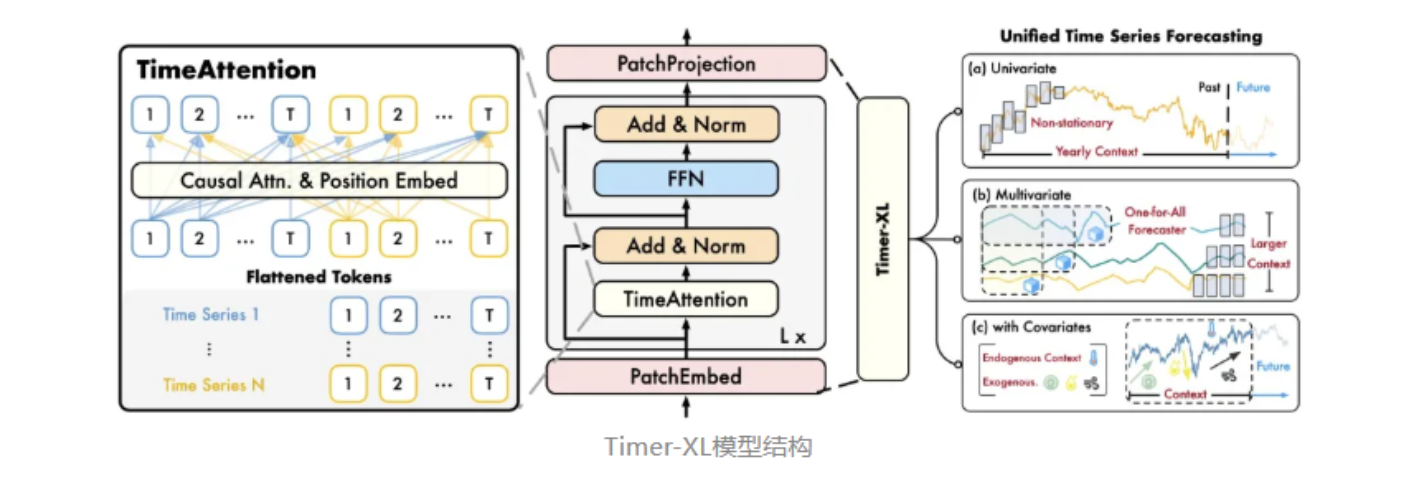
论文的关键创新:
- 多变量的下一个Token预测和统一的时间预测, 相比其他时序大模型, 考虑到多变量之间的依赖关系, 这使得模型具有更完备的上下文信息
- 针对多变量依赖关系,提出了TimeAtttention机制, 是一种为多维时间序列量身定制的新型因果自注意力机制,促进了具有位置意识的序列内和序列间建模
TimeAttention详细解释:
下一词预测:
下一词预测(Next Token Prediction)是大语言模型的主流训练目标。其核心在于训练时并行优化在多个位置上 的自回归预测信号,推理时,模型可基于不同的上下文长度进行预测。本工作将该范式首次扩展到多变量时间序列
多变量下一词预测:
基于分块(Patching)后的二维时间序列单元,每个位置的下一词预测不仅依赖于该序列的历史变化(时序因果性),还依赖于相关变量的外生关联.
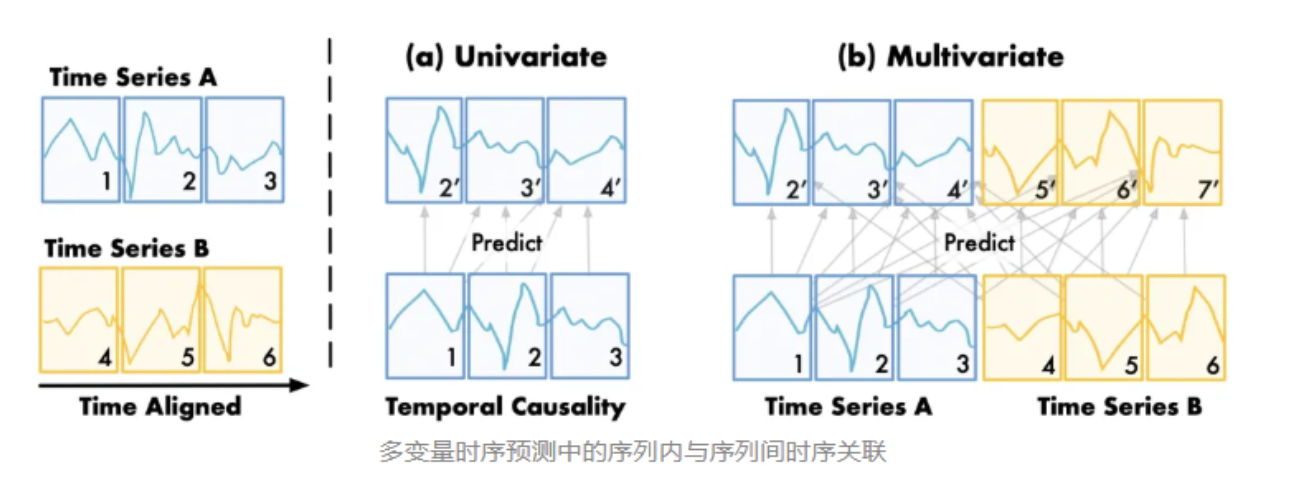
Timer的核心:
通过**克罗内克积(Kronecker Product)**将"变量间的空间依赖 "与"时间步上的因果依赖 "解耦并重组。
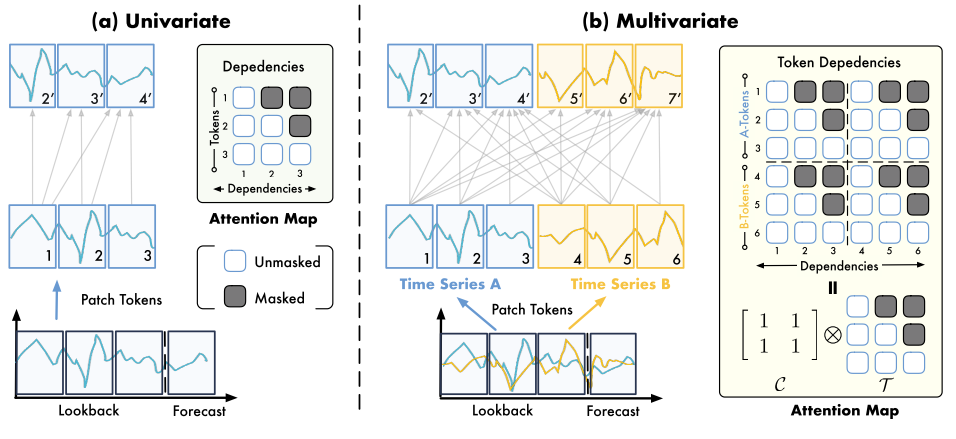
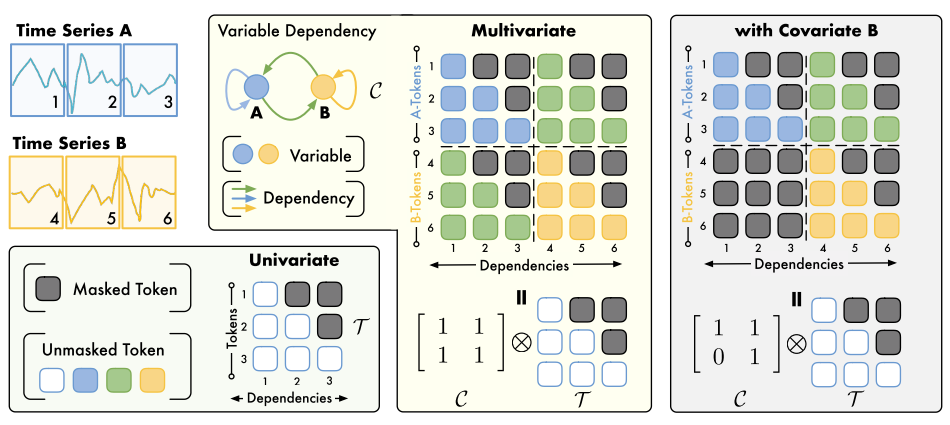
TimeAttention捕获patch之间的依赖性, 按照时间顺序将二维时间序列展平为一维时间序列.
原问题 : 针对协变量:它的矩阵 C\mathcal{C}C是 [1101]\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}[1011],而不是 [[1,1]]?
问题改写: 如果我们只预测 A,只需要知道 A 依赖 A 和 B 及其历史就行了,为什么还要管 B 依赖谁?
原因分析:
(1) Self-Attention 的输入形状 : 模型输入的 Token 序列不仅包含 Target A 的 Patch,也包含 Covariate B 的 Patch。假设我们有 2 个变量(A 和 B),每个变量切成 TTT 个 Patch,那么输入到 Attention 层的序列总长度是 2T2T2T。 Attention Map 的大小必须是 (2T)×(2T)(2T) \times (2T)(2T)×(2T)。这就要求变量依赖矩阵 C\mathcal{C}C 必须是 2×22 \times 22×2 的,才能通过克罗内克积扩展成完整的大小。
(2) 矩阵的每一行代表"谁在看":C=[1101]\mathcal{C} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}C=[1011] 这个矩阵要按行来解读:
第一行 (Row 1, Variable A) : [1,1][1, 1][1,1]。
这意味着:变量 A 的 Token (Query) 可以去 Attention 变量 A (Key) 和 变量 B (Key)。
物理意义:A 是我们要预测的目标,它既受自身历史影响,也受协变量 B 的影响。这符合直觉。
第二行 (Row 2, Variable B) : [0,1][0, 1][0,1]。
这意味着:变量 B 的 Token (Query) 只能 去 Attention 变量 B (Key),不能看变量 A。
物理意义 :这是"协变量"定义的关键。协变量通常被视为"外生变量" (Exogenous Variable),比如天气、节假日。
如果 C2,1=1\mathcal{C}_{2,1} = 1C2,1=1(即 B 依赖 A),那就意味着 A 的变化会导致 B 的变化(例如:商场销量 A 变了,导致天气 B 变了)。这显然是不符合逻辑的。
因此,为了保持 B 的纯粹性(它只按自己的规律演变,不受目标变量 A 的干扰),我们必须切断 A -> B 的注意力路径。这就是那个 0 的由来。
原问题: 为什么协变量和多变量的矩阵不一样?实际依赖关系不应该一样吗?
原因分析 : 在时间序列预测的建模中,"多变量预测" (Multivariate) 和 "带协变量的单变量预测" (Univariate with Covariate) 是两种完全不同的任务假设。
(1) 多变量 (Multivariate) 场景
任务定义 :同时预测 A 和 B。我们认为 A 和 B 是耦合系统 (Coupled System)。
依赖假设:互为因果。比如:A 是"高速公路流量",B 是"平均车速"。流量大了车速会慢(A -> B),车速慢了可能导致拥堵反过来影响流量分布(B -> A)。
矩阵体现 :C=[1111]\mathcal{C} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}C=[1111]。A 需要看 B 的历史来预测 A。B 也需要看 A 的历史来预测 B。这是一个双向图。
(2) 协变量 (Covariate) 场景
任务定义 :只预测 A,利用 B 作为辅助信息。我们假设 B 是驱动因素。
依赖假设 :单向因果。比如:A 是"冰淇淋销量",B 是"气温"。气温升高会增加销量(B -> A)。但销量增加绝对不会让气温升高(A -x-> B)。
矩阵体现 :C=[1101]\mathcal{C} = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}C=[1011]。A 依赖 B(利用气温预测销量)。B 不 依赖 A(计算气温的特征表示时,不需要看销量)。这是一个单向图。