INT303 Big Data Analysis 大数据分析 Pt.11 模型选择和词向量（Word Embeddings）

文章目录

[1. 模型选择](#1. 模型选择)
- [1.1 训练数据 vs 测试数据](#1.1 训练数据 vs 测试数据)
- [1.2 泛化（Generalization）](#1.2 泛化（Generalization）)
- [1.3 模型选择的原则](#1.3 模型选择的原则)
- [1.4 数据集划分](#1.4 数据集划分)
- - [1.4.1 K折交叉验证（K-fold Cross Validation）](#1.4.1 K折交叉验证（K-fold Cross Validation）)
  - [1.4.2 留一法交叉验证（Leave-One-Out Cross Validation，LOOCV）](#1.4.2 留一法交叉验证（Leave-One-Out Cross Validation，LOOCV）)
  - [1.4.3 Python代码](#1.4.3 Python代码)
  - [1.4.4 示例](#1.4.4 示例)
  - [1.4.5 考虑模型复杂度](#1.4.5 考虑模型复杂度)
  - - [1.4.5.1 决策树的复杂度与泛化误差](#1.4.5.1 决策树的复杂度与泛化误差)
    - [1.4.5.2 多项式回归的例子。](#1.4.5.2 多项式回归的例子。)
- [1.5 模型选择的本质](#1.5 模型选择的本质)
- [1.6 参数与超参数的区分](#1.6 参数与超参数的区分)
- [1.7 小结](#1.7 小结)
[2. 词向量（Word Embeddings）](#2. 词向量（Word Embeddings）)
- [2.1 词向量的核心训练算法](#2.1 词向量的核心训练算法)
- - [2.1.1 Continuous Bag of Words（CBOW）](#2.1.1 Continuous Bag of Words（CBOW）)
  - [2.1.2 Skip-gram（SG）](#2.1.2 Skip-gram（SG）)
- [2.2 词向量的效果](#2.2 词向量的效果)

1. 模型选择

我们上次说到我们对模型有很多评估标准。

但是光有评估标准是不够的，我们还要考虑一些其他方面。

1.1 训练数据 vs 测试数据

如果我们的模型只是为了训练而训练，那样我们就会出现过拟合（Overfitting）。

模型过度拟合了训练数据中的无意义模式，这种现象叫"过拟合"。

因此我们需要将模型放在新的数据上进行评估，这便是测试数据。

如果模型在训练集上误差很小，但在测试集上误差很大，说明模型过拟合了，不能真正泛化到新数据。如图所示。

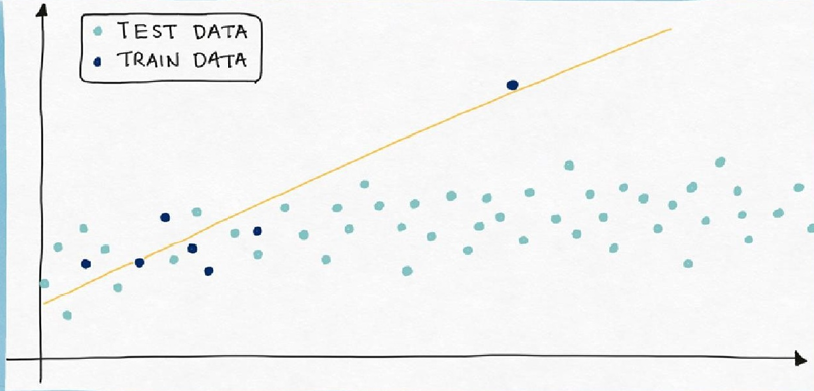
训练数据的均方误差MSE是2.0，但是测试数据的MSE是12.3。

1.2 泛化（Generalization）

有些模型在训练数据上表现很好，但一遇到新数据就表现不佳。这正是我们前面讲的过拟合（overfitting）。

泛化（Generalization）正是模型在没见过的数据上仍然表现良好的能力。

因此我们模型选择不是选训练误差最小的模型而是泛化能力最强的模型。

而评估泛化的方式是泛化误差，它指的是模型在新数据（测试集或真实世界数据）上的误差。

1.3 模型选择的原则

我们需要用一套有原则的方法，来进行模型选择。而选择模型正是为了决定模型应该复杂到什么程度，从而避免过拟合。

这里包括选用那些特征（predictores）、用多高阶的多项式、模型里包含多少交叉项等。

所以现在前面那句话应该理解为：用一套有原则的方法，来决定模型的复杂度。

所以我们做模型选择的动机视为了防止过拟合。

常见的几种典型过拟合来源：

特征太多（too many predictor）包含：
-- 特征空间维度太高（the feature space has high dimensionality）
-- 多项式阶数太高（the polynomial degree is too high）
-- 考虑了太多交叉项（too many cross terms are considered）
系数太极端（coefficients too extreme）

1.4 数据集划分

因此我们会像前面一样进行数据集划分。

将数据集划分为训练集（Train）和测试集（Test）。

但是这样我们可能会反复试不同模型，一直看 test 结果来调模型，测试集就渐渐变成了我们的训练集。

所以仅靠一次train--test split，不足以安全地做模型选择。

所以我们引入了验证集（Validation）。

验证集（Validation）用来进行模型选择，比较不同模型 / 超参数，决定用什么特征，多项式阶数，正则化强度等。

训练集（Train）用来学习模型参数，真正参与拟合。

测试集（Test）则是在最后使用，用来反馈模型的最终性能。它绝对不能参与训练或模型选择。

但其实我们如果反复用同一个验证集来选模型，模型会逐渐"迎合"这个验证集。这便是对验证集过拟合。所以我们如果换一批数据，其的效果可能并不好。

因此我们可以取多个不同的验证集进行评估，再取平均。

这样可以降低偶然性，并且拥有更稳定的估计泛化能力。

1.4.1 K折交叉验证（K-fold Cross Validation）

但是如果知识多次随机划分数据，有些重要模式 / 特征可能在多次随机抽样中始终没被抽到或没被充分代表。

因此我们下面介绍一种系统的解决方案而非简单的随机抽样------K折交叉验证（K-fold Cross Validation）

我们把原来原来的训练集，平均分成多块，轮流当验证集，其余的当训练集。

k-fold的意思是一共有 k 块，每一块都会当一次验证集，其余 k−1 块用于训练。

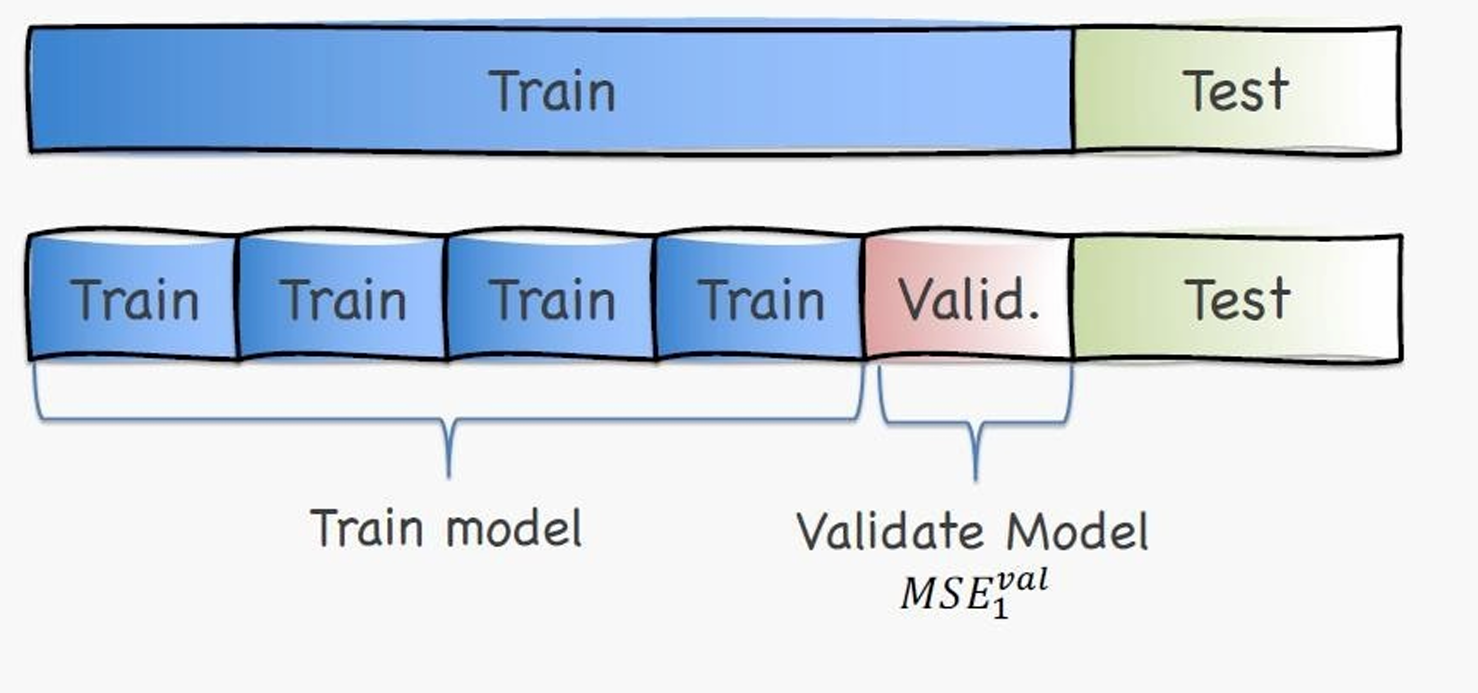
如图所示，这里是5-fold，红色的用作Validation时，别的4块就用作Train。

下一次就会是这样。

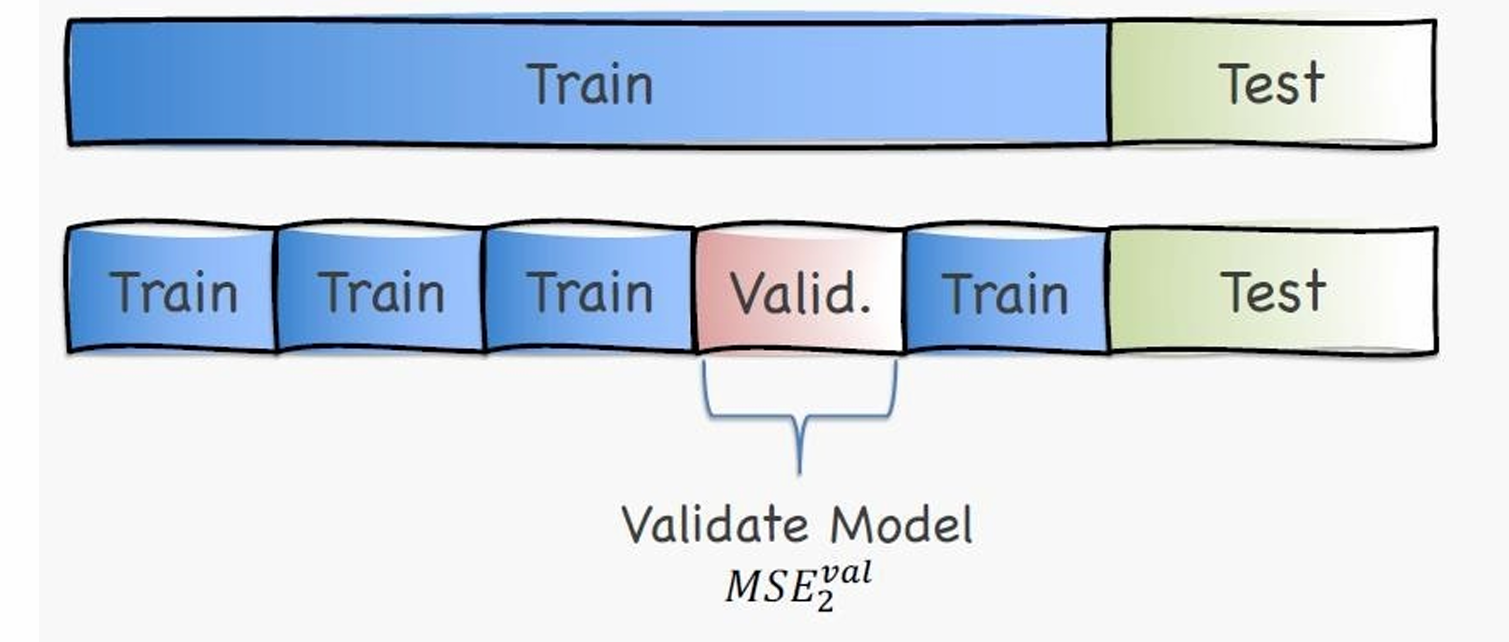
用另一块作为Validation，其余用作Train。

以此类推。

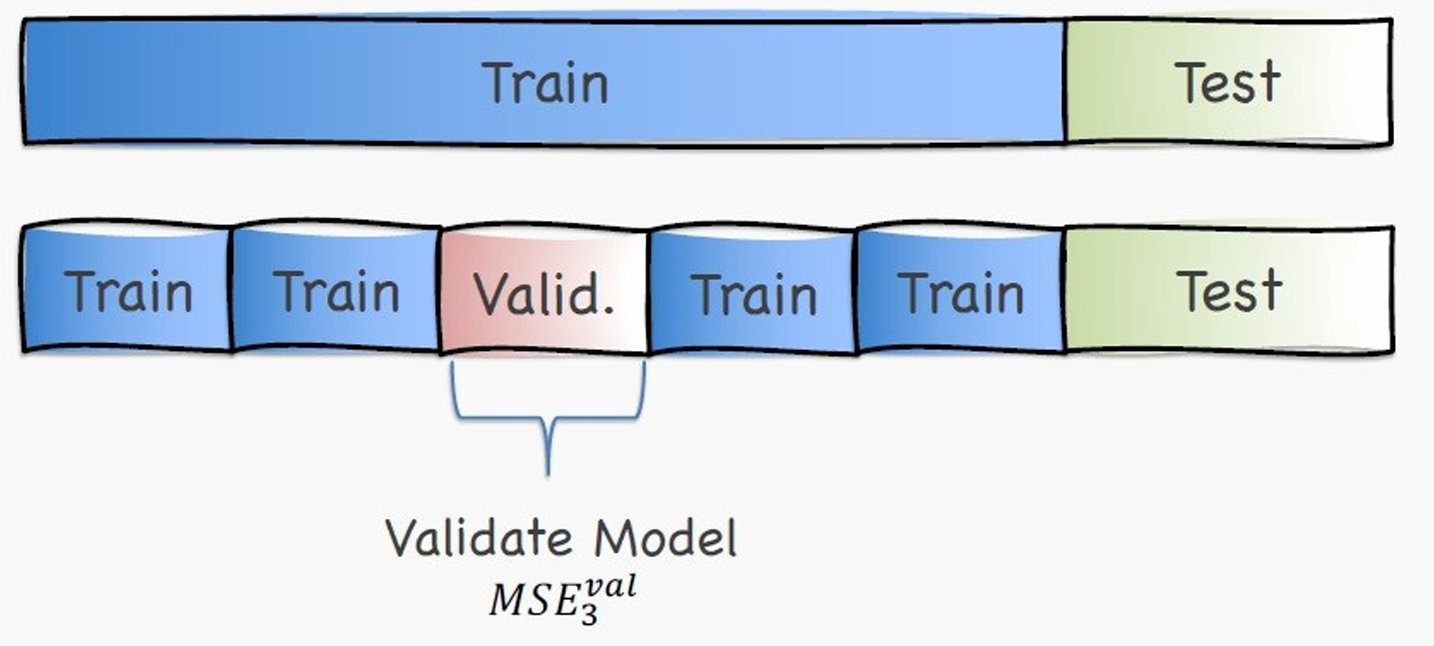
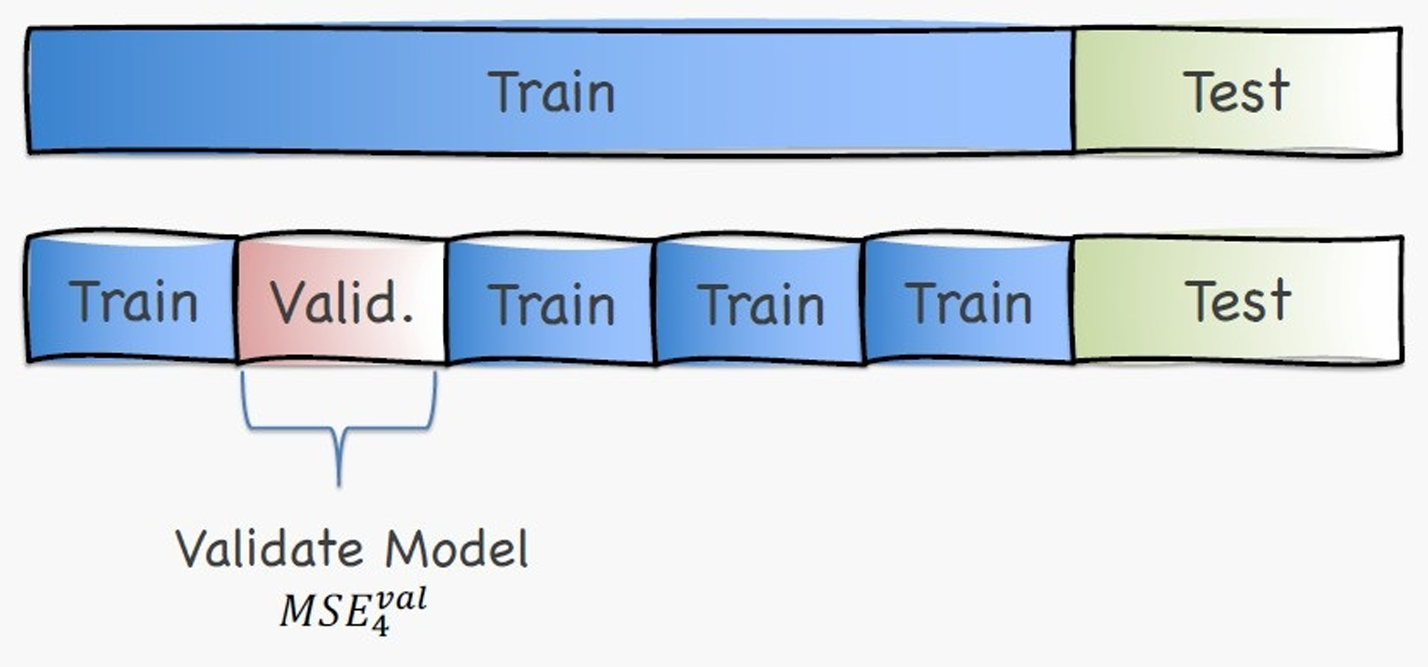
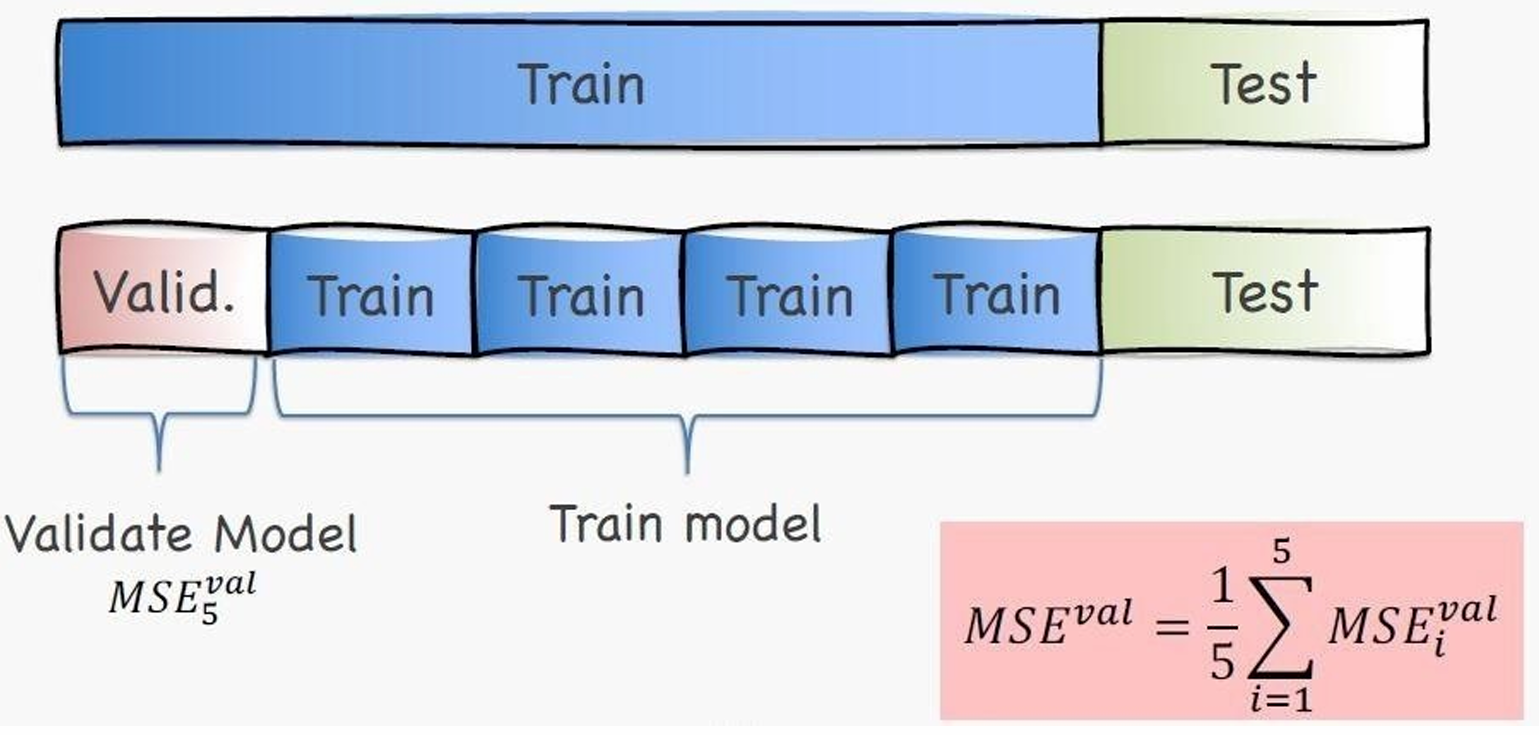
我们把这5次验证误差取平均就可以得到一个稳定的验证误差估计，我们就可以用它来比较模型 / 选超参数。
M S E v a l = 1 5 ∑ i = 1 5 M S E i v a l \mathrm{MSE}^{val} = \frac{1}{5}\sum_{i=1}^{5} \mathrm{MSE}_i^{val} MSEval=51∑i=15MSEival

1.4.2 留一法交叉验证（Leave-One-Out Cross Validation，LOOCV）

我们还有另一种类似的方式，它是刚刚k折交叉验证的一个极端特例。

Leave-One-Out（留一法）的核心思想是：每次只留 1 个样本做验证，其余所有样本都用来训练。

如果你一共有 n 个样本。就要训练 n 次模型，每一次都换一个样本当验证集。

数学表达为：

Validation Set： { X i } \{X_i\} {Xi}

Traing Set： X − i = { x 1 , . . . , X i − 1 , X i + 1 , . . . , X n } X_{-i}=\{x_1,...,X_{i-1},X_{i+1},...,X_n\} X−i={x1,...,Xi−1,Xi+1,...,Xn}，也就是除了第 i i i个样本以外，其余 n − 1 n-1 n−1个样本全部用于训练。

对于每一次循环（ i = 1 , . . . , n i=1,...,n i=1,...,n)，我们先用训练集 X − i X_{-i} X−i拟合模型 f ^ X − i \hat f_{X_{-i}} f^X−i。

然后用该模型在被留下的样本 X i X_i Xi上进行预测 f ^ X − i ( X i ) \hat f_{X_{-i}}(X_i) f^X−i(Xi)。

再计算该样本的损失（误差） L ⁣ ( f ^ X − i ( X i ) ) L\!\left(\hat f_{X_{-i}}(X_i)\right) L(f^X−i(Xi))。

最后的交叉验证分数那就是这些结果再取平均值： C V ( Model ) = 1 n ∑ i = 1 n L ( f ^ X − i ( X i ) ) \mathrm{CV}(\text{Model}) = \frac{1}{n} \sum_{i=1}^{n} L(\hat f_{X_{-i}}(X_i)) CV(Model)=n1∑i=1nL(f^X−i(Xi))。

1.4.3 Python代码

我们使用scikit-learn库种对应的cross_validate函数就能轻松实现交叉验证。

python 复制代码

sklearn.model_selection.cross_validate(
    estimator, X, y, scoring, cv, return_train_score
)

其中estimator是我要用的模型。

X是输入特征（feature matrix），形状一般是 (n_samples, n_features)，也就是训练数据。

y是目标变量（label），回归里是真实值，分类里是类别。

scoring是评价指标。回归常用：

python 复制代码

scoring="neg_mean_squared_error"

注意：scikit-learn 里越大越好，所以 MSE 要取负号（neg_）。

cv是交叉验证的折数。cv=n 等价于 LOOCV。

return_train_score表示是否返回训练误差。True：同时给你训练误差 + 验证误差。可以用来判断是否过拟合。

1.4.4 示例

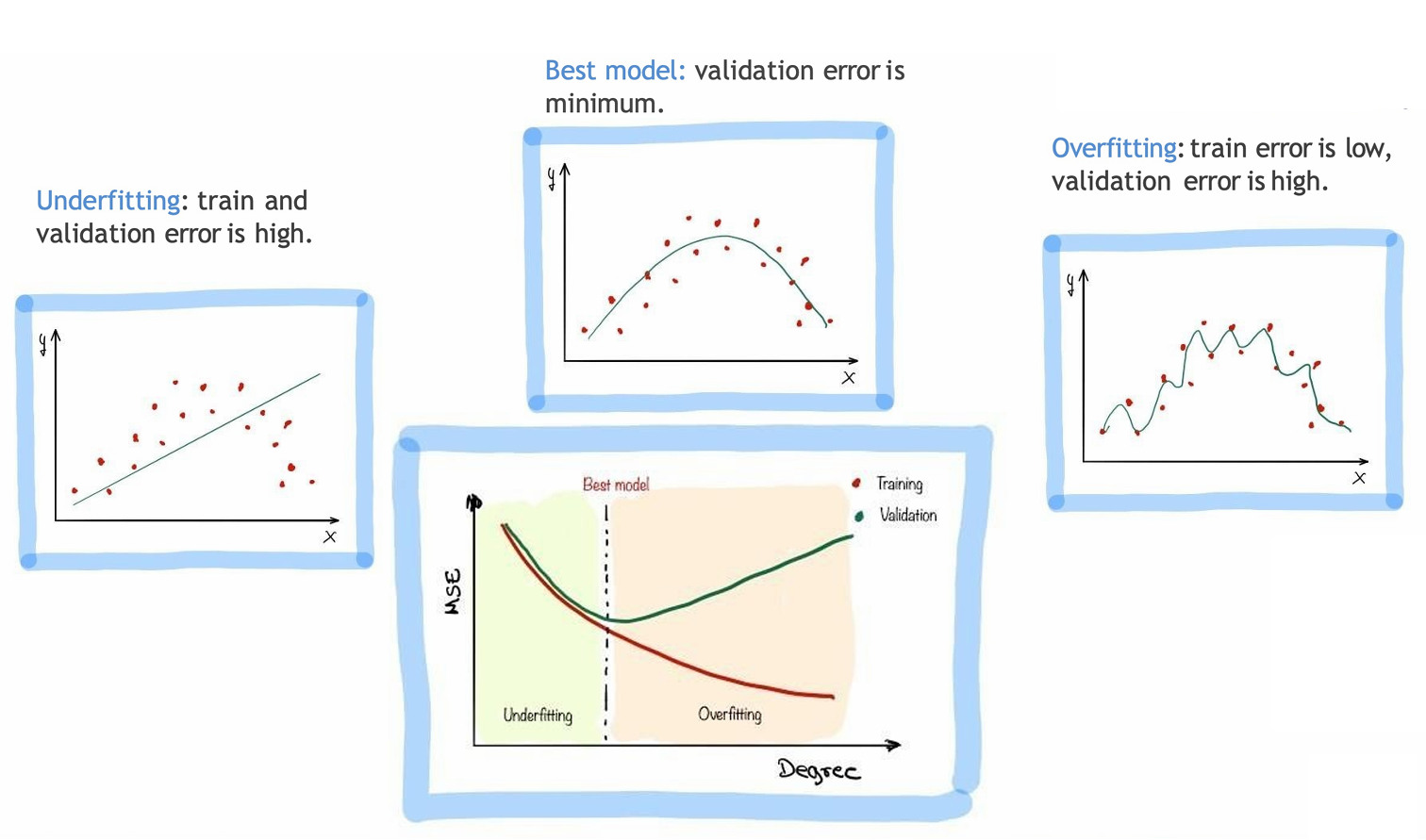
例如下图我们给出了一张评估结果。

训练误差和我们前面说的一样，它会随着训练进行不断变小，这就是过拟合。

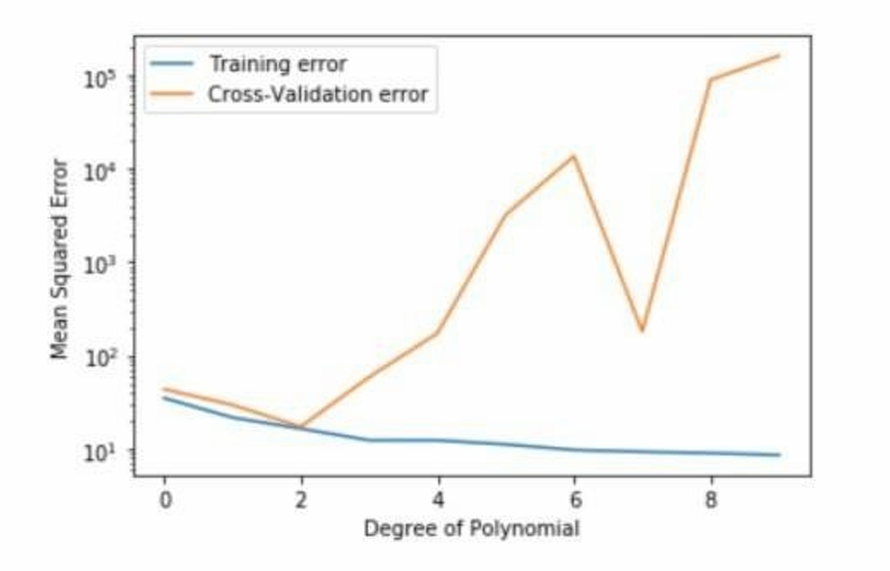
我们这里使用交叉验证误差作为标准选择合适的多项式系数。因此我们的选择标准是交叉验证误差最小。这里黄线先降后升，正好是因为模型欠拟合 → 合适 → 过拟合。所以这里最合适的多项式系数是2。

1.4.5 考虑模型复杂度

我们在模型选择时还需要考虑模型复杂度。

核心思想来自奥卡姆剃刀（Occam's razor），也是正则化、AIC/BIC 等方法的思想源头。

奥卡姆剃刀（Occam's razor）指出在解释能力差不多的情况下，越简单越好。

也就是如果两个模型泛化误差差不多，优先选更简单的那个。

为什么复杂模型不值得轻易选？

复杂模型更容易"偶然拟合"。容易把噪声当成规律。
泛化不稳定。对数据扰动非常敏感。
解释性更差。参数多，结构复杂。

公式为：
Gen. Error(Model) = Train Error(Model, Train Data) + α × Complexity(Model) \text{Gen. Error(Model)} = \text{Train Error(Model, Train Data)} + \alpha \times \text{Complexity(Model)} Gen. Error(Model)=Train Error(Model, Train Data)+α×Complexity(Model)

其中 Train Error \text{Train Error} Train Error当然是模型的误差，模型越复杂，这个值通常越小。
Complexity(Model) \text{Complexity(Model)} Complexity(Model)衡量模型的复杂度。
α \alpha α是复杂度惩罚的权重，越大就越偏向简单模型。

1.4.5.1 决策树的复杂度与泛化误差

我们可以用训练误差来当作泛化误差的估计。

也就是说，在同一批训练数据上，既训练模型，又评估模型，这种做法叫重代入（resubstitution）。

这种做法是过于乐观的（optimistic）。因为模型是专门为这批训练数据拟合的。尤其是决策树，其可以不断分裂从而记住每个样本，所以训练误差一定偏小而低于真实的泛化误差。

如下图所示。

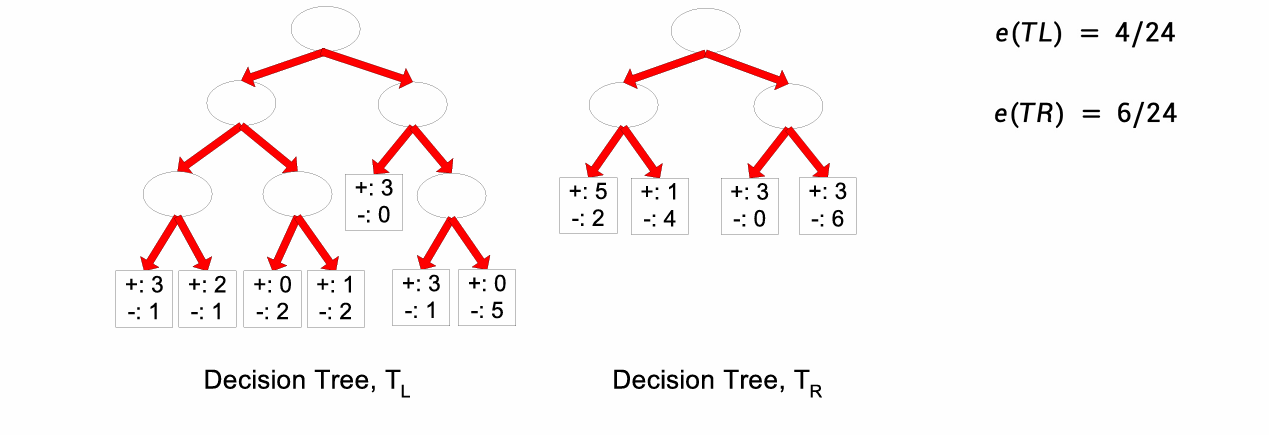
左树错了 4 个，右树错了 6 个。按训练误差左边更好，但是它结构更复杂、分裂更多，这很可能是偶然拟合训练数据，所以可能对新数据泛化更差。

因此仅凭训练误差，会偏向选择过于复杂的树。

所以重代入（resubstitution）不适合用来做模型选择，尤其是对决策树。

因此我们现在试着把模型复杂度纳入误差估计。这种方法叫做悲观误差估计（Pessimistic Error Estimate）。它的目的非常明确：防止决策树因为太复杂而过拟合。
e r r g e n ( T ) = e r r ( T ) + Ω × k N t r a i n \mathrm{err}{gen}(T)=\mathrm{err}(T)+\Omega \times \frac{k}{N{train}} errgen(T)=err(T)+Ω×Ntraink

其中， e r r ( T ) \mathrm{err}(T) err(T)是决策树 T T T在训练集上的错误率，叶子节点数 k k k用于度量模型复杂度， N t r a i n N_{train} Ntrain是训练样本总数， Ω \Omega Ω控制误差与复杂度之间的权衡。

我们用这个重新计算一下我们前面的例子。

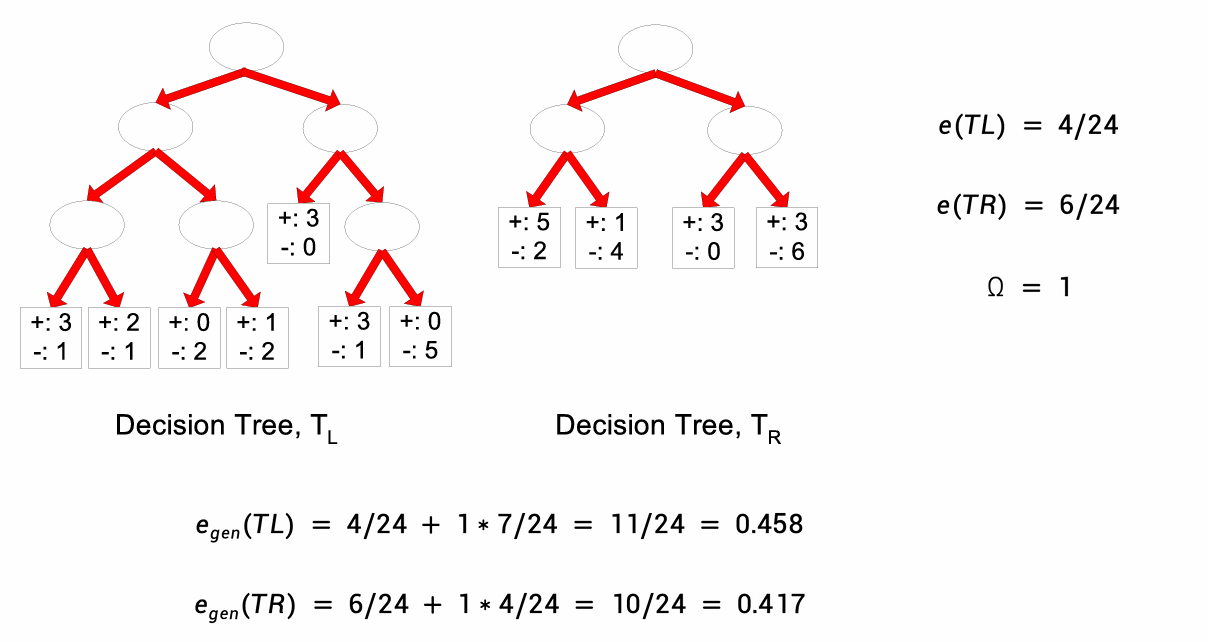
我们可以发现用悲观误差估计的结果是右边的决策树更好。

1.4.5.2 多项式回归的例子。

用多项式去拟合一组数据时，应该选多复杂的多项式？

这里把其评估结果拆成两种成本（cost）：

Model cost（模型复杂度）：
多项式有多复杂（阶数、系数多少、幅度多大）
Data cost（拟合误差）：
模型预测值和真实数据之间的差异

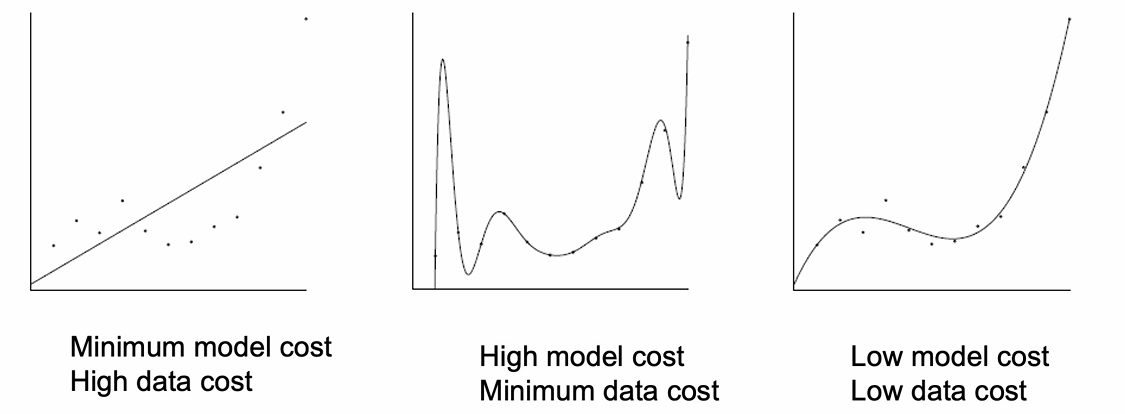
我们可以看到左图低模型复杂度但是高拟合误差，也就是欠拟合。
中间的图高模型复杂度但是低拟合误差，这是过拟合。
而右边的图模型足够灵活，但不过度扭曲，这便是最佳折中的结果。
我们可以使用MDL来自动避免过拟合。
MDL 的核心思想是选择"描述数据 + 描述模型"总长度最短的模型。
形式上可以理解为 Total Cost = Model Cost + Data Cost \text{Total Cost}=\text{Model Cost}+\text{Data Cost} Total Cost=Model Cost+Data Cost

1.5 模型选择的本质

模型选择其实就是在"调超参数"，而超参数控制的是模型复杂度。

下面的例子展示了这一点。

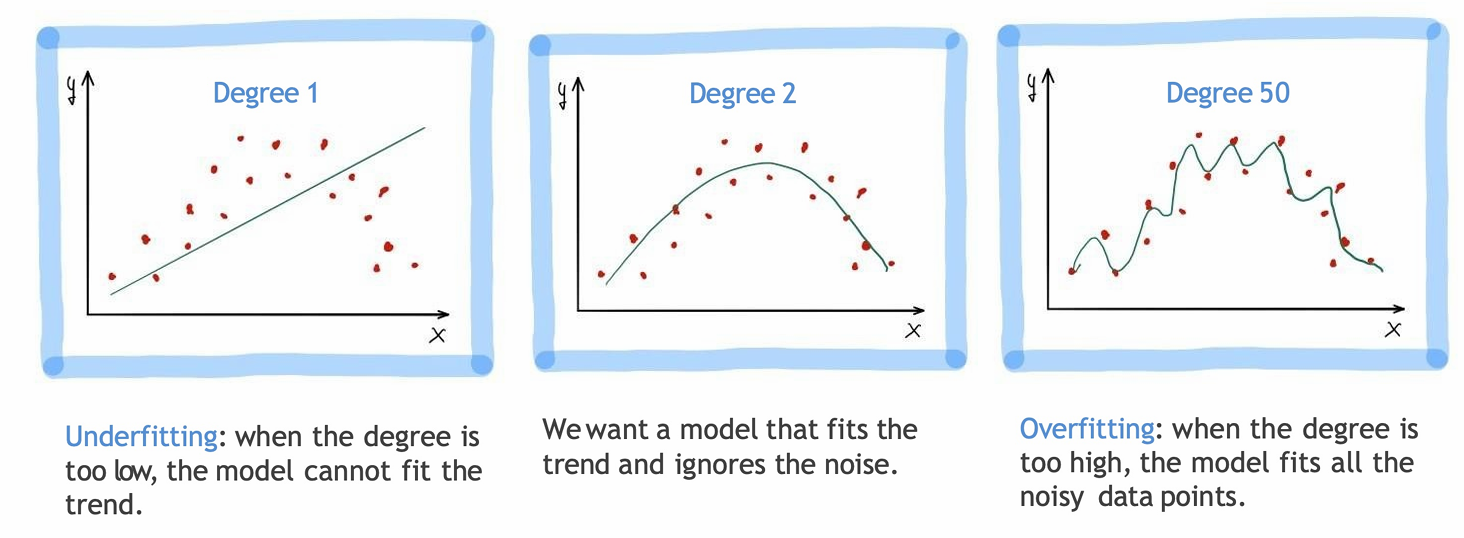
我们选择不同的模型就是在选择不同的超参数。

也就是说，模型选择可以转化为超参数选择，而多项式回归中"阶数"就是控制欠拟合与过拟合的关键超参数。

1.6 参数与超参数的区分

我们用一张表格清晰区分这两个概念。

对比维度	参数（Parameters）	超参数（Hyperparameters）
谁来设定？	模型 / 算法自动学习	人（数据科学家）手动设定
什么时候确定？	训练过程中	训练开始之前
如何得到？	通过优化算法从数据中估计（如最小化损失函数）	通过经验、网格搜索、交叉验证等方式选择
是否依赖训练数据？	是，直接由训练数据决定	间接影响训练过程，但不直接从数据中学
主要作用	用于做预测	控制模型复杂度和学习过程
是否参与预测？	是，直接用于预测	否，只影响模型训练方式
是否属于模型本身？	是，模型的一部分	否，属于模型外部设定
和模型选择的关系	固定模型后由训练决定	模型选择的核心对象
典型例子（回归）	线性回归的权重、截距	多项式回归的阶数（degree）
典型例子（决策树）	每个节点的划分规则	最大深度 `max_depth`、叶子数
典型例子（正则化）	回归系数本身	正则化强度 α / λ

1.7 小结

我们前面选择的主要是两种进行模型选择的方式。

基于验证集 / 测试集的方法（数据驱动）
我们不只用训练集，而是用未参与训练的数据进行评估，代表方法有：k-fold cross validation、LOOCV。
优点：

非常直观。
理论上最可靠。
不依赖模型形式。

缺点：

需要额外数据。
计算成本高（尤其 CV）。

考虑模型复杂度的方法（模型驱动 / 解析式）
我们只用训练集，不用新数据，而是通过惩罚复杂度来修正训练误差，代表方法有：决策树悲观误差估计、正则化（Ridge / Lasso）、AIC / BIC / MDL。
优点：

不需要验证集。
计算快。
可解释性强。

缺点：

是近似 / 启发式。
依赖复杂度定义是否合理。

2. 词向量（Word Embeddings）

词向量（Word Embeddings）是用一个词在大量上下文中的"邻居"来表示这个词的含义。

或者说一个词的含义，可以通过它经常一起出现的其他词来刻画。

也就是说我们可以看一个词经常和谁一起出现从而知道这个词是什么意思。

这是现代 NLP 最成功的思想之一。在词向量出现之前：词是 one-hot（离散、互不相关）。例如："bank"和"money"在数学上毫无关系。

而词向量之后：词被表示成连续向量，语义相近的词就会表示为向量距离近，因此模型可以"理解"语义相似性。

词向量不是人为定义的，而是从大量文本中统计学地学出来的。下图展示了这个例子。

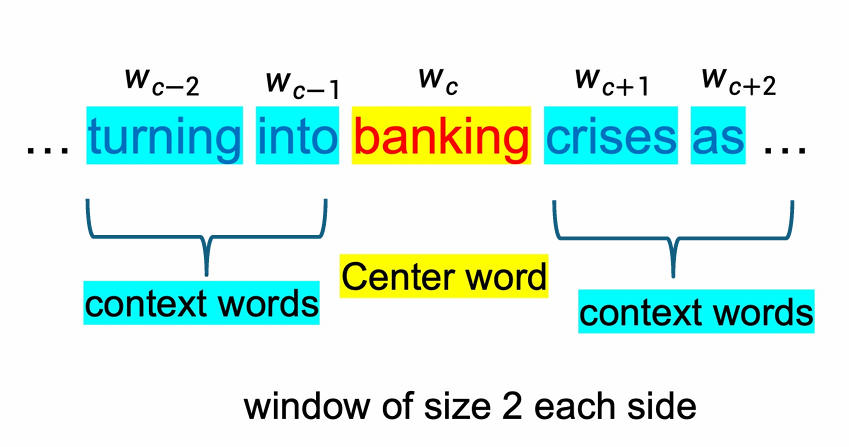
我们要学习的词将是中心词（Center word），上下文词（Context words）是出现在中心词附近的词，这里这个窗口大小是2，也就是两边各2个词，一共是4个上下文词（Context words）。

2.1 词向量的核心训练算法

词向量的核心训练算法有两个：

Skip-gram（SG）
给定中心词，预测它周围的上下文词。
P ( w c − 1 ∣ w c ) , P ( w c − 2 ∣ w c ) , P ( w c + 1 ∣ w c ) , P ( w c + 2 ∣ w c ) P(w_{c-1}\mid w_c),\; P(w_{c-2}\mid w_c),\; P(w_{c+1}\mid w_c),\; P(w_{c+2}\mid w_c) P(wc−1∣wc),P(wc−2∣wc),P(wc+1∣wc),P(wc+2∣wc)
Continuous Bag of Words（CBOW）
给定上下文词，预测中心词。
P ⁣ ( w c ∣ w c − 2 , w c − 1 , w c + 1 , w c + 2 ) P\!\left( w_c \mid w_{c-2},\, w_{c-1},\, w_{c+1},\, w_{c+2} \right) P(wc∣wc−2,wc−1,wc+1,wc+2)

我们需要注意的是，这里位置是独立的，它们的地位完全一样。因此不会因为距离而有不同的影响，它们都是单纯地被认为是普通上下文词。

2.1.1 Continuous Bag of Words（CBOW）

刚刚提到了Continuous Bag of Words（CBOW）是用一个上下文窗口里的词，来预测中间的中心词。

所以CBOW 不是学"一个词向量"，而是学两套词向量。

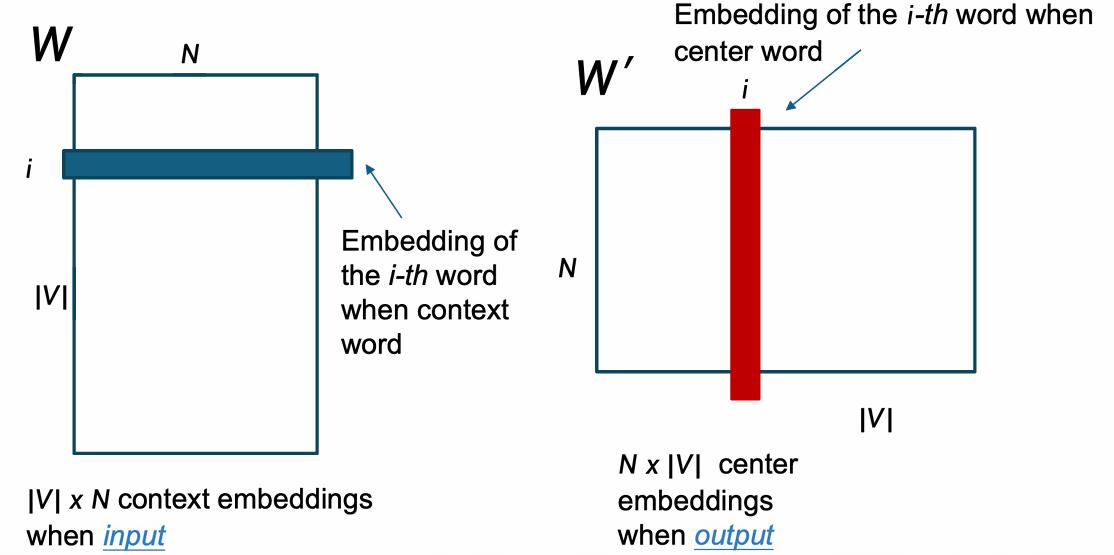
第一个矩阵 W W W是输入 / 上下文词向量。

大小为： W ∈ R ∣ V ∣ × N W \in \mathbb{R}^{|V| \times N} W∈R∣V∣×N

其中 ∣ V ∣ |V| ∣V∣是词表大小。
N N N是词向量维度。

第二个矩阵 W ′ W' W′是输出 / 中心词向量。

大小为： W ′ ∈ R N × ∣ V ∣ W' \in \mathbb{R}^{N\times |V| } W′∈RN×∣V∣

其中 ∣ V ∣ |V| ∣V∣是词表大小。
N N N是词向量维度。

因此同一个词作为上下文词时，用 W W W中的向量。

作为中心词时，用 W ′ W' W′中的向量。

因此步骤如下：

输入2m个one-hot向量，它们是上下文词。
x ( c − m ) , ... , x ( c − 1 ) , x ( c + 1 ) , ... , x ( c + m ) x^{(c-m)}, \ldots, x^{(c-1)}, x^{(c+1)}, \ldots, x^{(c+m)} x(c−m),...,x(c−1),x(c+1),...,x(c+m)
根据one-hot计算Embedding。
v c − m = W x ( c − m ) , ... , v c − 1 = W x ( c − 1 ) , v c + 1 = W x ( c + 1 ) , ... , v c + m = W x ( c + m ) v_{c-m} = W x^{(c-m)}, \;\ldots,\; v_{c-1} = W x^{(c-1)}, \; v_{c+1} = W x^{(c+1)}, \;\ldots,\; v_{c+m} = W x^{(c+m)} vc−m=Wx(c−m),...,vc−1=Wx(c−1),vc+1=Wx(c+1),...,vc+m=Wx(c+m)
对上下文向量求平均。
v ^ = v c − m + v c − m + 1 + ⋯ + v c + m 2 m , v ^ ∈ R N \hat{v}= \frac{v_{c-m} + v_{c-m+1} + \cdots + v_{c+m}}{2m}, \qquad \hat{v} \in \mathbb{R}^N v^=2mvc−m+vc−m+1+⋯+vc+m,v^∈RN
生成 score 向量
z = W ′ v ^ z = W' \hat{v} z=W′v^
将这个向量结果转化为对所有此的概率分布
y ^ = s o f t m a x ( z ) \hat{y} = \mathrm{softmax}(z) y^=softmax(z)
p i = e z i ∑ j e z j p_i = \frac{e^{z_i}}{\sum_j e^{z_j}} pi=∑jezjezi
我们希望中心词的概率接近 1。

下面我们给出一个例子。

我们的例句是The cat sat on floor。这里的窗口大小是2，中心词是sat。

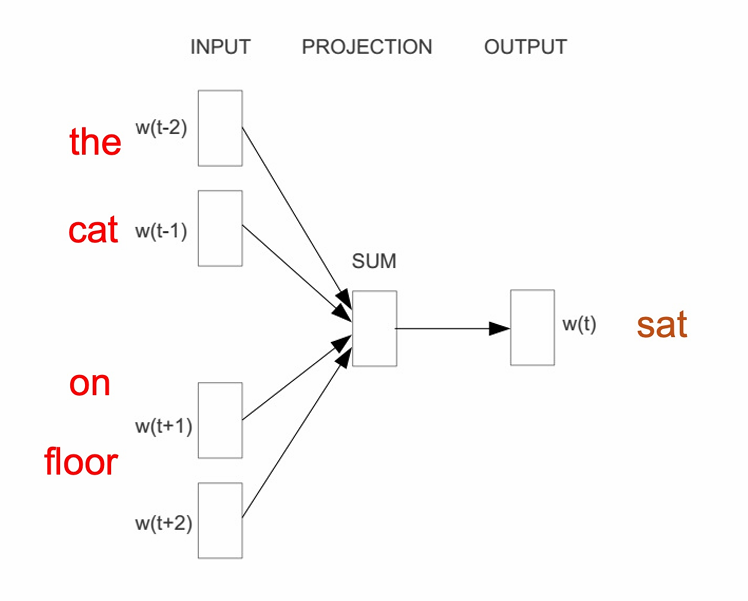
我们输入这个句子的上下文词the,cat,on,floor之后其对每个上下文词计算embedding，然后进行求和，最后输出概率分布，也就是用上下文词预测中心词sat。

我们下面更详细地查看这个例子。

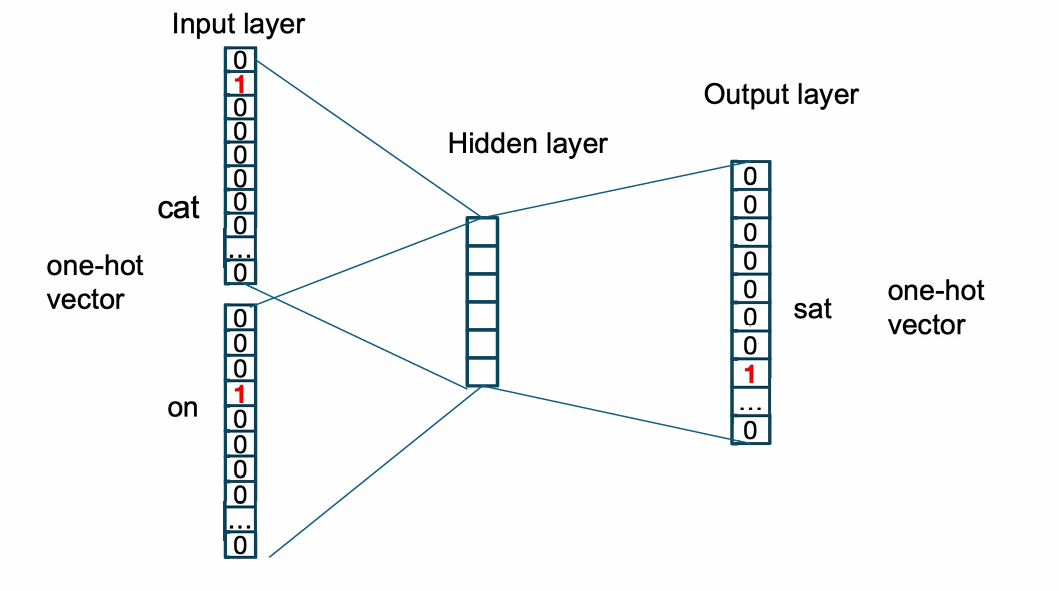
我们刚刚提到了输入是one-hot vector，输出地时候其实也是one-hot vector。

我们用我们的输入embedding矩阵与输入的one-hot vector相乘就能计算出对应的embedding。

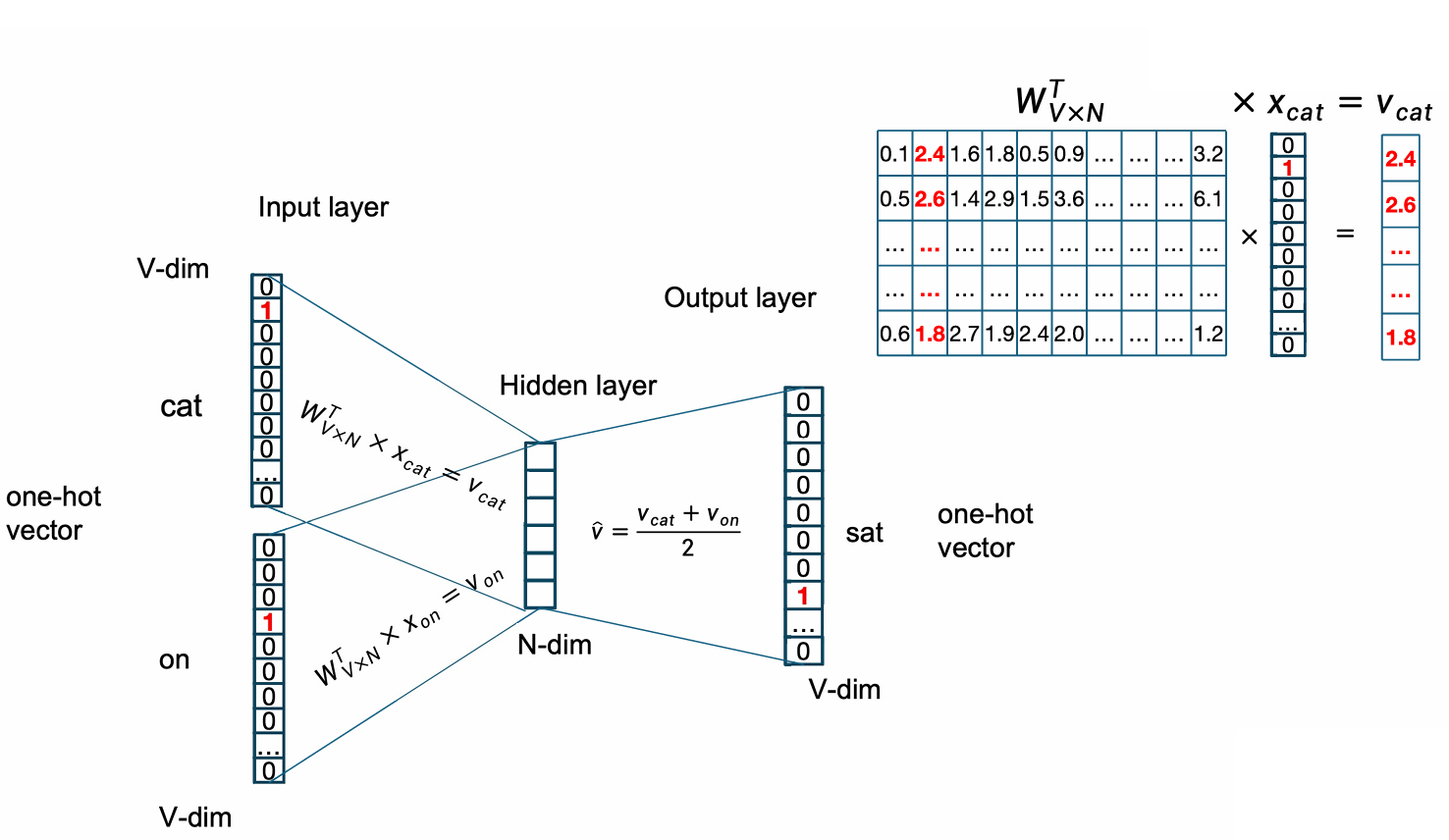
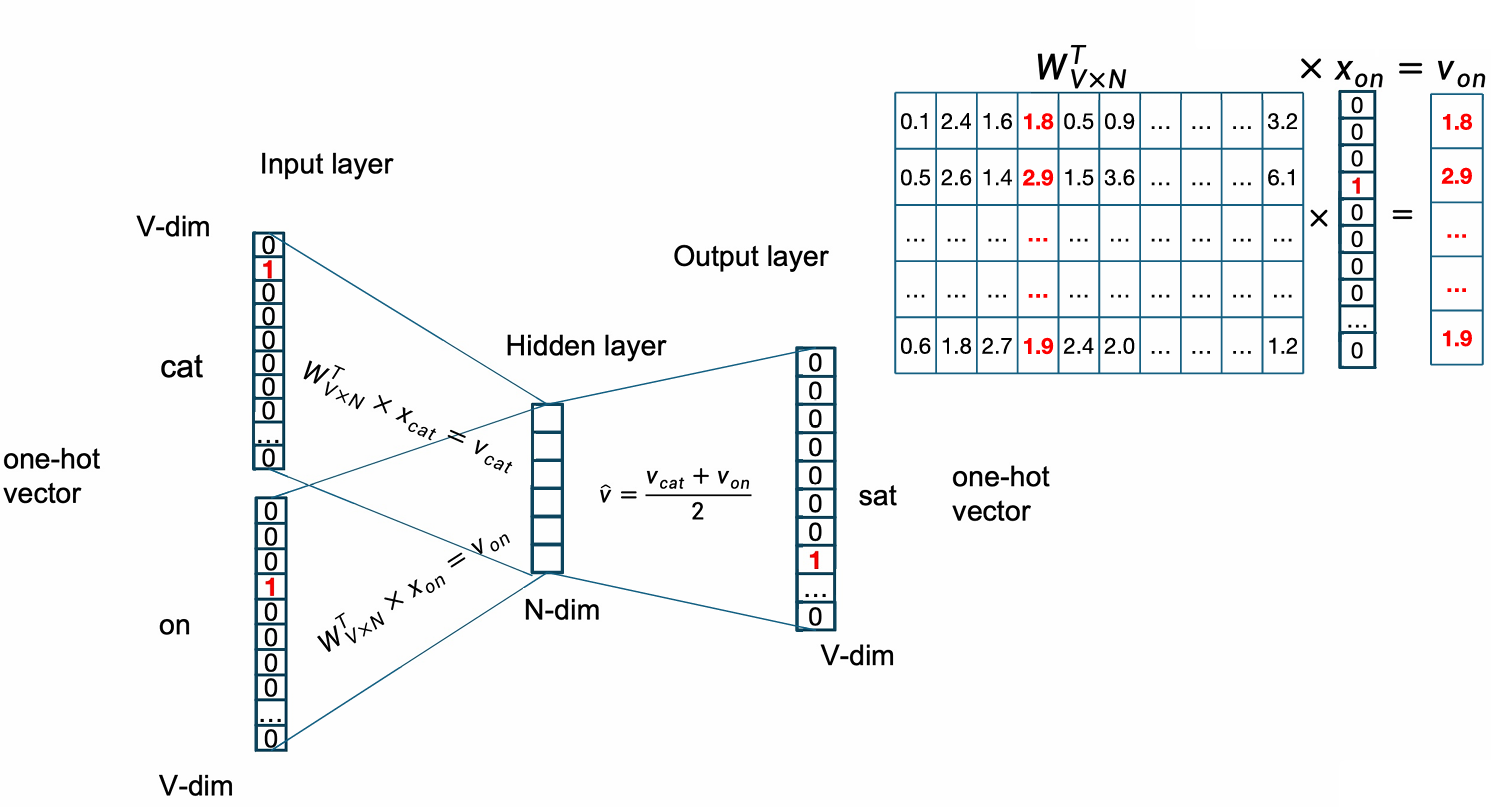
下一步是计算embedding的均值。

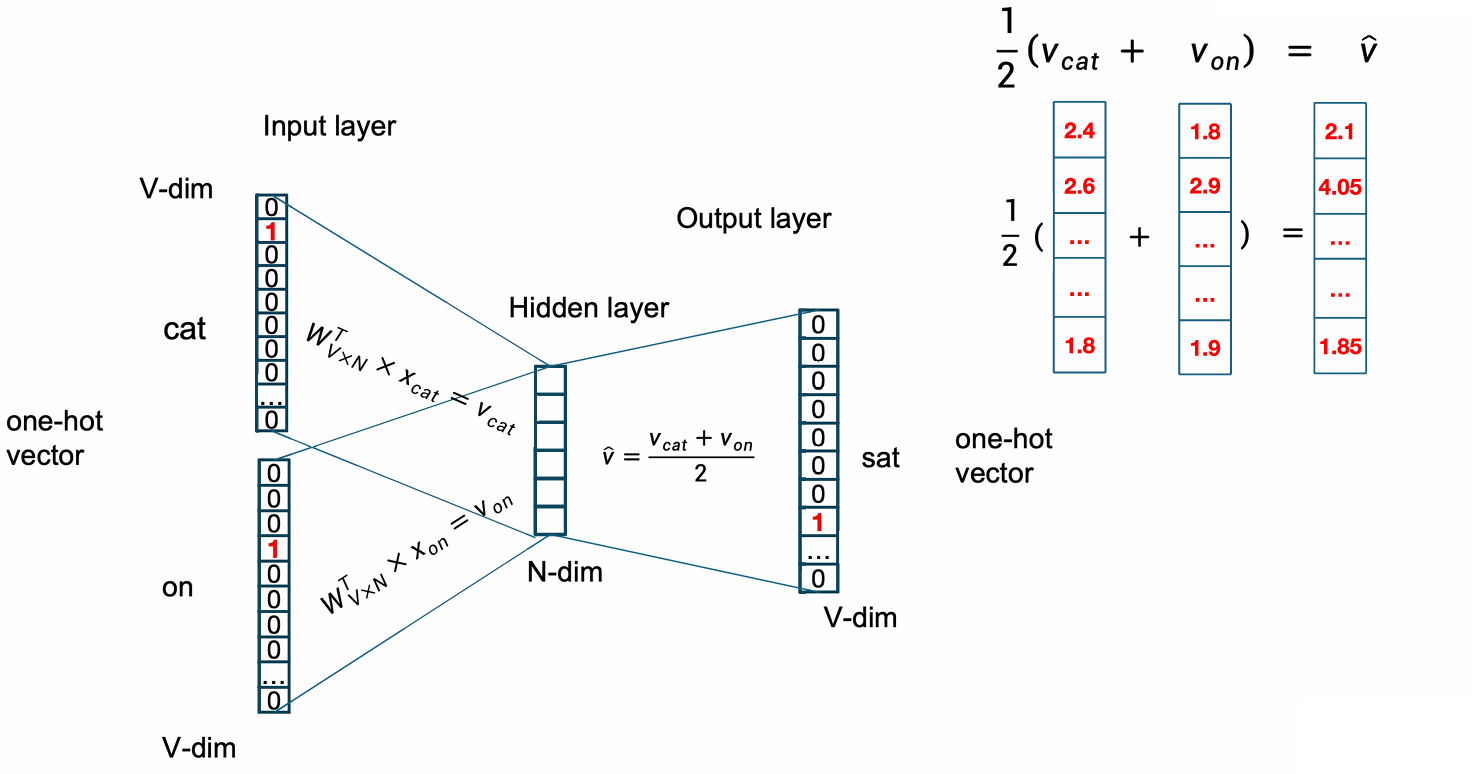
然后我们用输出矩阵 W ′ W' W′计算打分。
z = W ′ v ^ z = W' \hat{v} z=W′v^

然后用softmax将其变成概率分布。

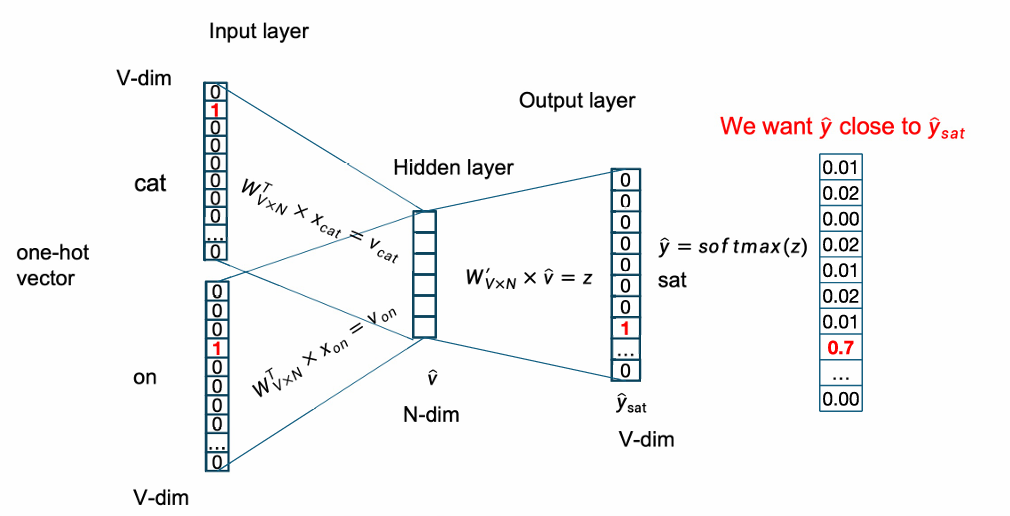
我们训练的目标是让预测分布尽量接近真实的 one-hot 分布。

在这个Word2Vec里，每个词其实学到了两套向量。

一套来自 W W W（作为上下文词时）。

一套来自 W ′ W' W′（作为中心词时）。

最终做词向量时，我们可以使用 W W W或者 W ′ W' W′，甚至是两者的平均值。

2.1.2 Skip-gram（SG）

和 CBOW 正好相反 SG 用于输入中心词而预测其的上下文词。

同样其也要学习两个矩阵。

第一个矩阵 W W W是输入 / 中心词向量矩阵。

大小为： W ∈ R N × ∣ V ∣ W \in \mathbb{R}^{N\times |V| } W∈RN×∣V∣

其中 ∣ V ∣ |V| ∣V∣是词表大小。
N N N是词向量维度。

第二个矩阵 W ′ W' W′是输出 / 上下文词向量矩阵。

大小为： W ′ ∈ R ∣ V ∣ × N W' \in \mathbb{R}^{|V| \times N} W′∈R∣V∣×N

其中 ∣ V ∣ |V| ∣V∣是词表大小。
N N N是词向量维度。

因此具体步骤如下：

输入中心词的 one-hot vector。
x c ∈ R ∣ V ∣ x^c \in \mathbb{R}^{|V|} xc∈R∣V∣
计算得到中心词的 embedding。
v c = W x c v_c = W x^c vc=Wxc
计算所有上下文词的 score。
z = W ′ v c z = W' v_c z=W′vc
用 Softmax 得到概率。
y ^ = s o f t m a x ( z ) \hat{y} = \mathrm{softmax}(z) y^=softmax(z)

我们希望其训练结果上下文词的概率接近 1。

因为我们这里训练不是针对一个词，而是语料中有多个中心词 w t w_t wt，我们要最大化模型生成窗口内所有上下文词的概率。

因此是如果我们的语料中有 T T T个词，那么对每个位置 t t t，把 w t w_t wt当作中心词，然后每个中心词还有对应的窗口半径。我们希望这些概率全部相乘的结果最大，而不是单个词的概率最大。

因此整个 Skip-gram 的整体似然函数是
J ′ ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 p ( w t + j ∣ w t ; θ ) J'(\theta)=\prod_{t=1}^{T} \prod_{\substack{-m \le j \le m \\ j \ne 0}} p\bigl(w_{t+j} \mid w_t; \theta\bigr) J′(θ)=∏t=1T∏−m≤j≤mj=0p(wt+j∣wt;θ)

这里直接乘很多概率会导致数值极小（下溢），不方便优化。

因此变成负对数似然
J ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 log ⁡ p ( w t + j ∣ w t ; θ ) J(\theta)= -\frac{1}{T} \sum_{t=1}^{T} \sum_{\substack{-m \le j \le m \\ j \ne 0}} \log p\bigl(w_{t+j} \mid w_t; \theta\bigr) J(θ)=−T1∑t=1T∑−m≤j≤mj=0logp(wt+j∣wt;θ)

这里 T T T是语料长度。
m m m是窗口半径。
w t w_t wt是第 t t t个词（中心词）。
w t + j w_{t+j} wt+j是上下文词。
v w c v_{w_c} vwc是中心词 embedding。
v w o ′ v'_{w_o} vwo′是上下文词 embedding。
θ = W , W ′ θ = {W, W'} θ=W,W′是模型参数。

下面的例子展示了这个过程。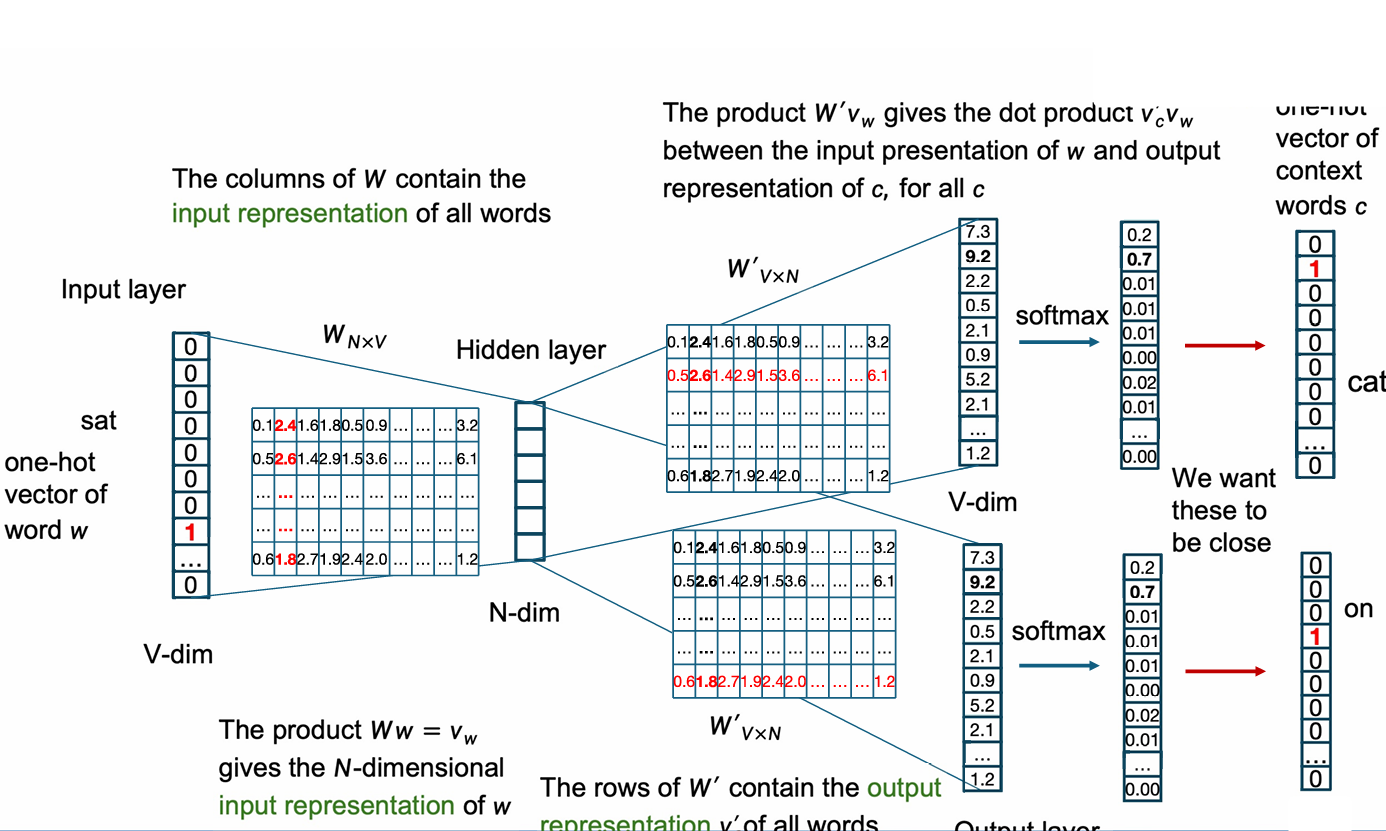

我们首先输入中心词的 one-hot 向量。

然后计算出对应的 embedding。

然后我们输出 score，这一步将中心词的 embedding 与 W' 中每一个词的输出 embedding 做点积，从而得到 score 向量。

然后使用 softmax 函数生成概率分布，从而得出预测的上下文词。

我们的训练希望这个结果与真实结果靠近。

我们这里使用的 softmax 公式为：
p ( c ∣ w ) = exp ⁡ ( v c ′ ⊤ v w ) ∑ i = 1 T exp ⁡ ( v i ′ ⊤ v w ) p(c \mid w) = \dfrac{\exp\left( v'c{}^{\top} v_w \right)}{\sum{i=1}^{T} \exp\left( v'_i{}^{\top} v_w \right)} p(c∣w)=∑i=1Texp(vi′⊤vw)exp(vc′⊤vw)

其中， T T T是语料库中的词数（词表大小）。
v w v_w vw是词 w w w的 input embedding。
v c ′ v'_c vc′是词 c c c的 output embedding。

示例如下。

Word	Input vector ( v w v_w vw)	Output vector ( v w ′ v'_w vw′)
King	[0.2, 0.9, 0.1]	[0.5, 0.4, 0.5]
Queen	[0.2, 0.8, 0.2]	[0.4, 0.5, 0.5]
Apple	[0.9, 0.5, 0.8]	[0.3, 0.9, 0.1]
Orange	[0.9, 0.4, 0.9]	[0.1, 0.7, 0.2]

同样这里有两套向量。

2.2 词向量的效果

下图是一个可视化效果，但是这里是高维词降维到二维平面后的结果。

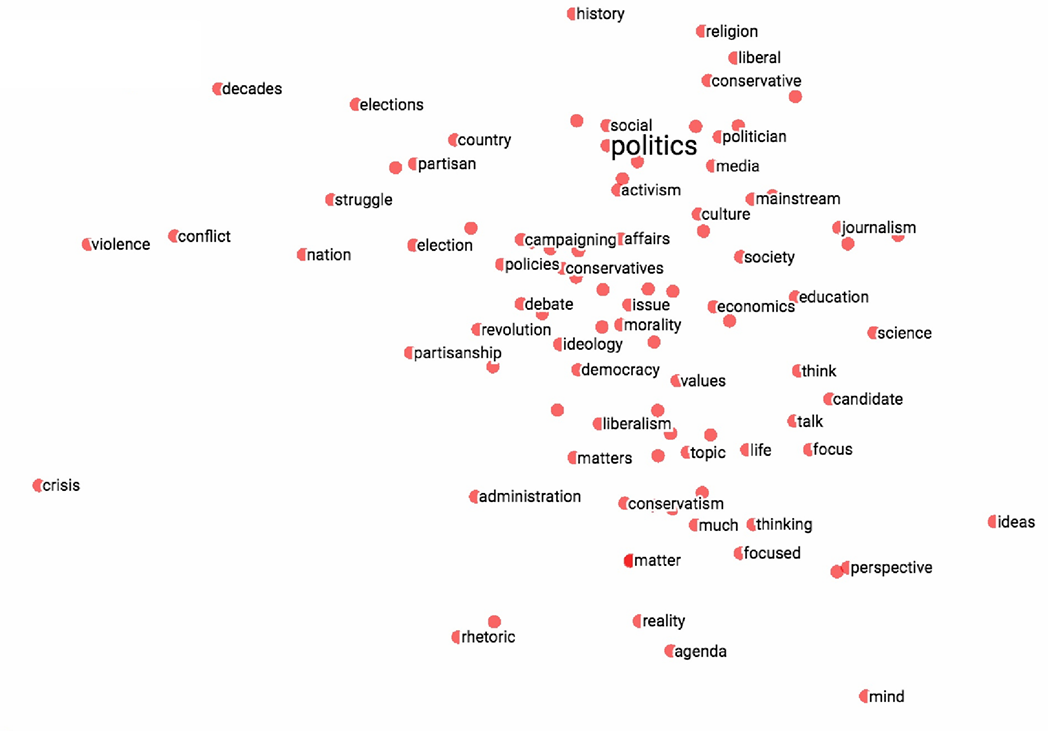
词向量的好处是其非常易于编码相似性（encoding similarity）和关系维度（dimensions of similarity）。

类比（Analogy）可以用向量减法解决。

在 embedding 空间里可以用 x A − x B ≈ x C − x D x_A-x_B≈x_C-x_D xA−xB≈xC−xD。

例如句法层面（Syntactic similarity）的单复数关系：

x_apple − x_apples ≈ x_car − x_cars ≈ x_family − x_families

不管是 apple、car 还是 family，这个"加 s"的变化向量是相似的。

同样的现象也适用于动词和形容词的形态变化（morphological forms）。

再比如语义层面（Semantic similarity）的类属关系（is-a）：

x_shirt − x_clothing ≈ x_chair − x_furniture

shirt 是 clothing 的一种，chair 是 furniture 的一种。

性别关系：

x_king − x_man ≈ x_queen − x_woman

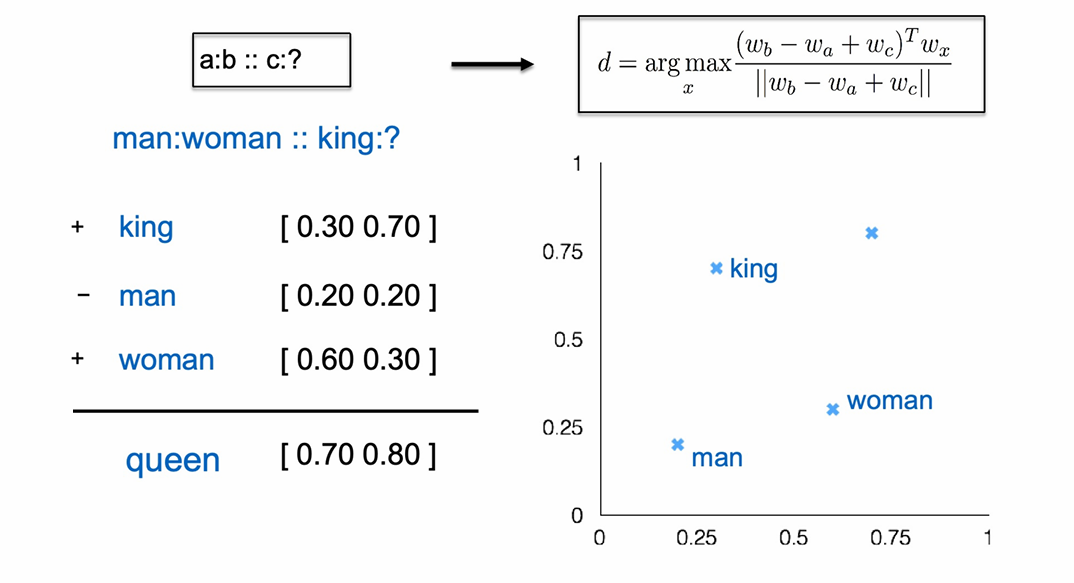
上图展示了刚刚性别关系的例子。我们可以通过x_king − x_man + x_woman ≈ x_queen的方式来找到表示queen的词，右上角是这个方法的数学表达，我们在词表里找这里与计算结果相似度最大的词。

这便是词向量不仅能表示"相似性"，还能表示"关系"。

而且这些关系在向量空间中是线性的。