题目
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
- LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
- int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
- void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
数据范围
1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105 最多调用 2 *
105 次 get 和 put
测试用例
java
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4题解(官解,双向链表+哈希,对于get与put时间复杂度为O1,空间位O(capacity))
java
class LRUCache {
class DLinkNode{
int key;
int value;
DLinkNode next;
DLinkNode pre;
public DLinkNode(){};
public DLinkNode(int key,int value){
this.key=key;
this.value=value;
}
}
HashMap<Integer,DLinkNode> map=new HashMap();
int size;
int capacity;
DLinkNode head;
DLinkNode tail;
public LRUCache(int capacity) {
head=new DLinkNode();
tail=new DLinkNode();
this.capacity=capacity;
this.size=0;
head.next=tail;
tail.pre=head;
}
public int get(int key) {
DLinkNode tl=map.getOrDefault(key,null);
if(tl==null){
return -1;
}else{
move(tl);
return tl.value;
}
}
public void put(int key, int value) {
DLinkNode tl=map.getOrDefault(key,null);
if(tl==null){
add(key,value);
}else{
tl.value=value;
move(tl);
}
}
public void add(int key,int value){
DLinkNode td=new DLinkNode(key,value);
td.next=head.next;
td.pre=head;
head.next=td;
td.next.pre=td;
map.put(key,td);
size++;
if(size>capacity){
remove();
}
}
public void remove(){
map.remove(tail.pre.key);
tail.pre.pre.next=tail;
tail.pre=tail.pre.pre;
size--;
}
public void move(DLinkNode tnode){
map.remove(tnode.key);
tnode.pre.next=tnode.next;
tnode.next.pre=tnode.pre;
size--;
add(tnode.key,tnode.value);
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/题解2(博主垃圾题解,可以不用看,纯处刑自己,tle了)
java
class LRUCache {
int capacity;
int cnt=0;;
PriorityQueue<tmap> queue=new PriorityQueue(new Comparator() {
@Override
public int compare(Object o1, Object o2) {
return ((tmap)o1).times-((tmap)o2).times;
}
});
public LRUCache(int capacity) {
this.capacity=capacity;
}
public int get(int key) {
int res=0;
for(tmap a:queue){
if(a.key==key){
res=a.value;
tmap t=new tmap(a.key,a.value,cnt++);
queue.remove(a);
queue.add(t);
return res;
}
}
return -1;
}
public void put(int key, int value) {
for (tmap a : queue) {
if (a.key == key) {
queue.remove(a);
queue.add(new tmap(key, value, cnt++));
return;
}
}
if (queue.size() == capacity) {
queue.poll();
}
queue.add(new tmap(key, value, cnt++));
}
}
class tmap{
int key;
int value;
int times;
public tmap(int key,int value,int times){
this.key=key;
this.value=value;
this.times=times;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/思路
这道题要求get与put时间复杂度都为O1,那么方法已经锁死了,使用双向链表加上哈希表,哈希表可以在存取做到O1,双向链表可以做到添加与删除的O1。因为博主实在很少手写链表,更何况双向链表,所以一开始做题完全没往这方向考虑。导致产出了一个tle。
博主认为这道题官解讲的不错这里直接引用。具体代码实现博主添加了详细的备注,大家都应该能看懂。
实现本题的两种操作,需要用到一个哈希表和一个双向链表。在面试中,面试官一般会期望读者能够自己实现一个简单的双向链表,而不是使用语言自带的、封装好的数据结构。在 Python 语言中,有一种结合了哈希表与双向链表的数据结构 OrderedDict,只需要短短的几行代码就可以完成本题。在 Java 语言中,同样有类似的数据结构 LinkedHashMap。这些做法都不会符合面试官的要求,因此下面只给出使用封装好的数据结构实现的代码,而不多做任何阐述。
`class LRUCache extends LinkedHashMap<Integer, Integer>{
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
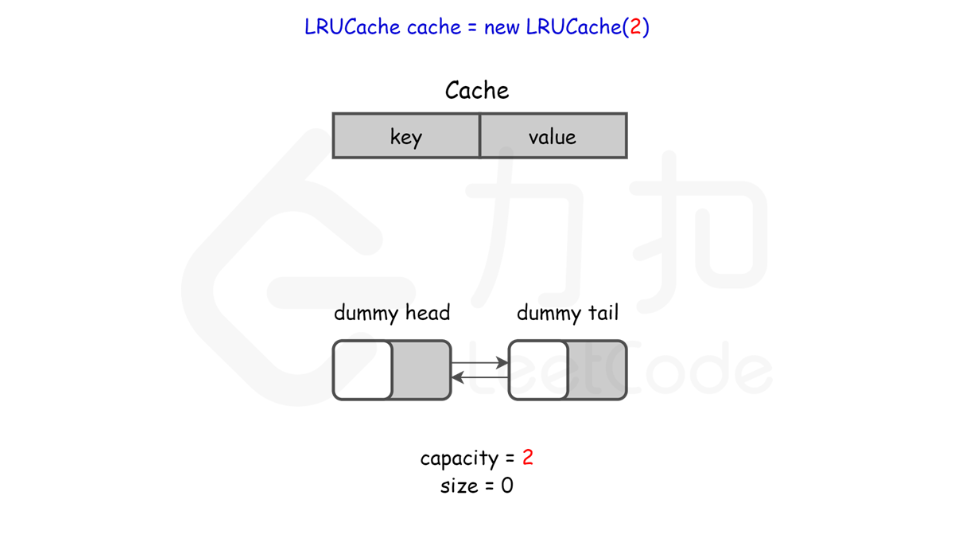
}LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 O(1) 的时间内完成 get或者 put 操作。具体的方法如下:
对于 get 操作,首先判断 key 是否存在:
如果 key 不存在,则返回 −1;
如果 key 存在,则 key对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 O(1),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为O(1)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 O(1) 时间内完成。