【递归算法】验证二叉搜索树

题目链接：验证二叉搜索树

文章摘要：

本文介绍了验证二叉搜索树（BST）的两种解法。解法一通过中序遍历存入数组检查有序性，但因内存消耗大被否决。解法二采用全局变量记录前驱节点值，递归判断左右子树和当前节点是否符合BST定义，并通过剪枝优化提前终止无效递归。关键点在于初始化前驱值为极小值（Long.MIN_VALUE）以避免边界问题，最终实现高效验证。

一、题目解析

根据所学，二叉搜索树（Binary Search Tree，后文的BST即代表二叉搜索树）的定义是：或者是一个空树/空节点，或者是满足以下性质的二叉树：

节点的左子树的值小于根节点的值
节点的右子树的值大于根节点的值
每一个节点的左子树和右子树都是二叉搜索树

而且BST的一个重要特性就是中序遍历的结果是一个有序的序列。

二、算法原理与代码实现

解法一（数组）

利用前面提到的性质，我们可以试着解这道题目：

中序遍历二叉树，将遍历到的节点的值存入数组中
遍历完成后，检查一下数组中的元素是否有序，若有序则返回true，否则返回false

这个解法看似可行，实则不然~

题目所给的节点数量将会非常大 ，这意味着，为了检查中序遍历的结果而创建的数组的长度也会非常大 ，这样非常消耗内存空间，因此该解法不可行。

解法二（全局变量）

我们采用维护全局变量的方式来解决。

定义一个全局变量prev，用于记录中序遍历时某节点的前驱节点的值，然后在递归过程中，对自身的值进行判断的时候（顺序：左 -> 自身 -> 右）就将节点的值与prev进行比较即可（就像前后双指针），当val > prev，该子树是BST，否则不是BST。

具体细节如下：

初始化prev为无穷小值，注意数据的范围
中序遍历：按照左中右的顺序，先判断左子树是否为BST，接着判断自身（比较val和prev的大小），然后判断右子树是否为BST
判断自身的细节：将prev与val比较，若val > prev，表示当前节点是BST，然后将prev的值更新成val；若val < prev，则当前节点不是BST，返回false。
当遇到空节点的时候，认为是BST，返回true

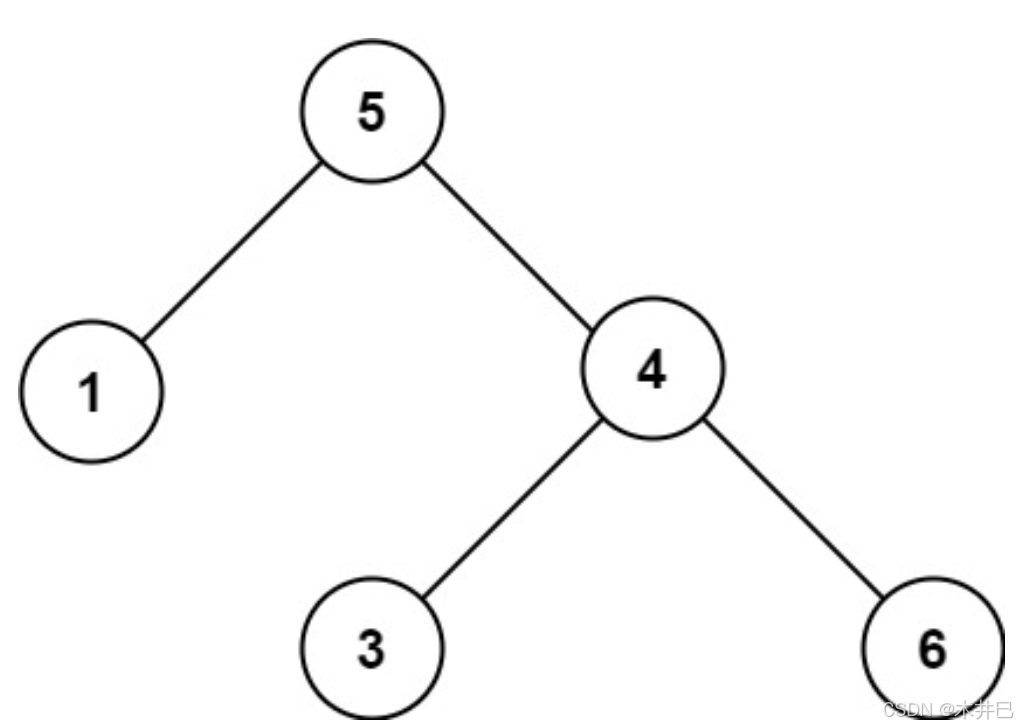
模拟过程：

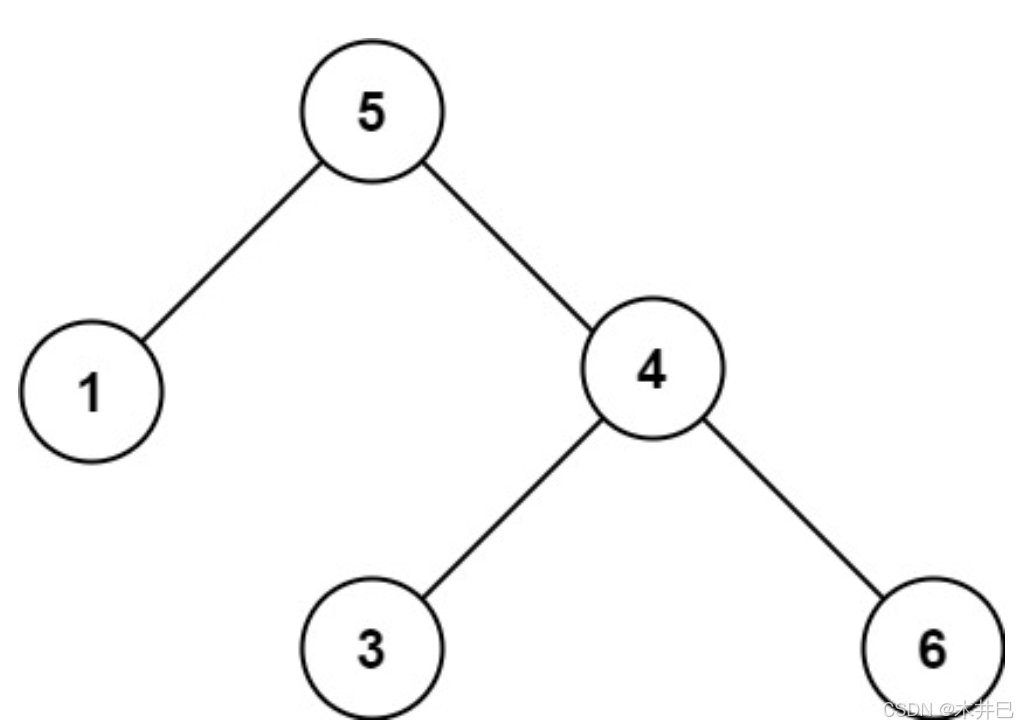
从根节点5开始进行中序遍历，此时将prev初始化为无穷小值。对于根节点5，先判断其左子树是否为BST
来到第一层根节点5的左子节点1，对于该节点1，先判断其左子树是否为BST
来到第二层节点1的左子节点null，此时遇到空节点，返回true
回到第二层节点1处，接下来判断自身，将prev（无穷小）与节点1的val进行比较，显然节点1的值 > prev，则节点1是BST，然后将prev的值更新为节点1的val，返回true
回到第一层根节点5处，此时其左子节点1已接受判断并确认为BST，接下来判断自身，将prev（1）与根节点5的val进行比较，根节点5的val > prev（1），则根节点5是BST，记录为true，然后将prev的值更新为根节点5的val。接着判断根节点5的右子树是否为BST
来到第一层根节点5的右子节点4，对于该节点先判断左子树是否为BST
来到第二层节点4的左子节点3，对于该节点先判断左子树是否为BST
来到第三层节点3的左子节点null，此时遇到空节点，返回true
回到第三层节点3处，接下来判断自身，将prev（5）与节点3的val进行比较，显然节点3的值 < prev（5），故节点3不是BST，返回false
回到第二层节点4处，此时其左子节点3已接受判断并已确认不是BST，接下来判断自身，将prev（5）与节点4的val进行比较，节点4的val < prev（5），故节点4也不是BST，记录为false。接着判断节点4的右子树是否为BST
来到第二层节点4的右子节点6，对于该节点先判断其左子树，为null，是BST。接下来判断自身，将prev（5）与节点6的val进行比较，节点6的val > prev（5），记录为true，并返回true
回到第二层节点4处，需要返回最终判断结果，当左子树、自身和右子树都满足BST的条件才返回true，否则返回false。对于节点4，其左子节点3不是BST，因此最终返回false
回到第一层根节点5处，需要返回最终判断结果。其右子树4不是BST，因此最终返回false
遍历完成，结果是false

需要注意的细节是数据的范围，prev我们初始化为Integer的最小值的时候，发现并不能够通过题目，原因是val可能刚好也是Integer的最小值（即-2³¹）：

将prev改成Long的最小值（-2⁶³）即可。

代码实现如下：

Java 复制代码

class Solution {
    long prev = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        // 递归出口
        if (root == null) return true;
		
	    // 判断左子树
        boolean left = isValidBST(root.left);
		
		// 判断自身val
        boolean cur = false;
        if (root.val > prev) cur = true;
        prev = root.val;

		// 判断右子树
        boolean right = isValidBST(root.right);

        // 返回
        return (left && cur && right);
    }
}

解法三（剪枝）

在刚刚的例子中，有两个情况可以直接得出结果：就是节点3和节点4不是BST的时候，可以直接一直返回false。因为一旦有一个节点不是BST，整个二叉树就不是BST，剩余的节点不管是否BST都不会影响到最终结果。

我们称已知某些情况下的操作无需再进行，以加快搜索的效率 这个操作为剪枝。

对解法二进行剪枝优化：

当判断完左子树时，检查一下返回值，若为false表示节点不是BST，这时候无需再判断自身val和右子树，可以直接返回到最终结果
当左子树已经确定是BST，并且判断完成自身时，检查一下记录的布尔值，若为false表示该节点不是BST，同样也无需再判断右子树，直接返回到最终结果

剪枝优化代码如下：

Java 复制代码

class Solution {
    long prev = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        // 递归出口
        if (root == null) return true;
		
	    // 判断左子树
        boolean left = isValidBST(root.left);
        // 剪枝
        if (left == false) return false;
		
		// 判断自身val
        boolean cur = false;
        if (root.val > prev) cur = true;
        prev = root.val;
        // 剪枝
        if (cur == false) return false;

		// 判断右子树
        boolean right = isValidBST(root.right);

        // 返回
        return (left && cur && right);
    }
}

完