【机器学习】人工神经网络（ANN）

目录

一、引言

二、核心原理与生物启发

三、核心结构与组件

[1. 层级结构](#1. 层级结构)

[2. 关键组件](#2. 关键组件)

四、训练机制：前向传播与反向传播

五、典型网络架构

六、发展历程

七、核心优势与应用场景

优势

应用

八、挑战与未来趋势

挑战

趋势

九、人工神经网络的Python代码完整实现

十、程序运行结果展示

十一、总结

---

一、引言

人工神经网络（Artificial Neural Network, ANN）是受生物神经系统启发的机器学习模型，核心是通过多层人工神经元的加权连接与参数优化，实现对复杂非线性关系的拟合与特征学习，是深度学习的基础。本文将详细讲解人工神经网络的算法原理以及Python代码完整实现。

二、核心原理与生物启发

• 生物原型：人脑由千亿级神经元通过突触连接，神经元整合输入信号后 "兴奋 / 抑制" 并传递信号；ANN 简化为 "加权求和 + 激活函数" 的数学模型，权重模拟突触强度，激活函数模拟神经元激活阈值。
• 数学本质：单个神经元的输出：

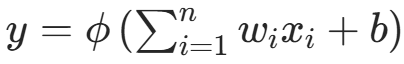
其中 为输入， 为权重，b 为偏置，ϕ 为激活函数，引入非线性以拟合复杂映射。

三、核心结构与组件

1. 层级结构

层级	功能	特点
输入层	接收原始数据（图像像素、文本向量等）	无计算，仅传递输入特征
隐藏层	特征提取与非线性变换	层数≥1 为深度网络，决定模型表达能力
输出层	输出预测结果（分类概率、回归值等）	节点数匹配任务（如二分类 1 个节点，多分类 N 个节点）

2. 关键组件

• 权重（Weights）：连接强度参数，训练中通过梯度下降优化，决定输入对输出的贡献度。
• 偏置（Bias）：调整激活阈值，避免模型仅拟合过原点的线性关系。
• 激活函数 ：引入非线性，常用类型如下：
  • Sigmoid：输出 (0,1)，适合二分类输出层，易梯度消失。
  • ReLU：max(0,x)，缓解梯度消失，广泛用于隐藏层。
  • Tanh：输出 (-1,1)，比 Sigmoid 中心对称，梯度更稳定。
  • Softmax：输出多分类概率分布，用于多分类输出层。

四、训练机制：前向传播与反向传播

1. 前向传播：输入数据经各层加权求和与激活，计算输出层预测值，同时记录各层激活值与中间结果。
2. 损失函数：衡量预测与真实标签的误差，如均方误差（MSE，回归）、交叉熵（分类）。
3. 反向传播（BP） ：
   • 从输出层反向计算各层参数的梯度（链式法则）。
   • 用优化器（SGD、Adam、RMSprop 等）更新权重与偏置，最小化损失函数。
4. 训练流程：初始化参数→前向计算→计算损失→反向求梯度→参数更新→迭代至收敛。

五、典型网络架构

1. 前馈神经网络（FNN）：信号单向传播，无循环，如全连接网络（FCN），用于简单分类 / 回归。
2. 卷积神经网络（CNN）：局部感知 + 参数共享，擅长图像、视频等网格数据，代表模型 AlexNet、ResNet。
3. 循环神经网络（RNN）：含时间循环连接，处理序列数据（文本、语音），LSTM/GRU 缓解梯度消失。
4. Transformer：基于自注意力机制，并行计算，主导 NLP（BERT、GPT）与多模态任务。
5. 生成模型：如 RBM、DBN、GAN，用于数据生成与无监督特征学习。

六、发展历程

1. 1943 年：McCulloch-Pitts 模型提出，首个神经元数学模型。
2. 1958 年：Rosenblatt 提出感知机，单层线性分类器，无法解决异或问题。
3. 1986 年：反向传播算法提出，推动多层网络训练。
4. 2012 年：AlexNet 在 ImageNet 夺冠，深度学习爆发，GPU 加速普及。
5. 2017 年至今：Transformer、大语言模型（LLM）成为主流，多模态融合快速发展。

七、核心优势与应用场景

优势

• 强大非线性拟合能力，可逼近任意复杂函数。
• 端到端学习，自动提取特征，减少人工特征工程。
• 分布式表示与容错性，部分节点损坏不影响整体性能。

应用

• 计算机视觉：图像分类、目标检测、语义分割、人脸识别。
• 自然语言处理：机器翻译、文本生成、情感分析、问答系统。
• 语音识别：语音转文字、声纹识别、语音合成。
• 其他：推荐系统、金融风控、医疗影像诊断、工业预测性维护。

八、挑战与未来趋势

挑战

• 黑箱问题：决策过程难解释，限制医疗、金融等关键领域应用。
• 数据依赖：需大量标注数据，小样本学习能力不足。
• 计算成本：深度模型训练需高性能 GPU/TPU，能耗高。
• 泛化性：易过拟合，需正则化（Dropout、L2）与数据增强。

趋势

• 可解释 AI（XAI）：提升模型透明度，如注意力可视化、梯度归因。
• 小样本 / 零样本学习：减少数据依赖，结合元学习、迁移学习。
• 神经形态计算：模仿人脑高效低功耗特性，开发专用芯片。
• 多模态融合：整合文本、图像、语音等数据，提升复杂任务性能。

九、人工神经网络的Python代码完整实现

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt
import numpy as np

# 1. 配置（CPU兼容，无需GPU）
device = torch.device("cpu")
batch_size = 32
learning_rate = 0.01  # 合成数据收敛更快，适当调高学习率
epochs = 20

# 2. 本地生成合成分类数据
# 生成3类二维数据，每类500个样本
np.random.seed(42)  # 固定随机种子，结果可复现
num_samples_per_class = 500

# 类别0：中心(0,0)的高斯分布
class0 = np.random.normal(loc=[0, 0], scale=0.5, size=(num_samples_per_class, 2))
labels0 = np.zeros(num_samples_per_class, dtype=np.int64)

# 类别1：中心(2,2)的高斯分布
class1 = np.random.normal(loc=[2, 2], scale=0.5, size=(num_samples_per_class, 2))
labels1 = np.ones(num_samples_per_class, dtype=np.int64)

# 类别2：中心(0,3)的高斯分布
class2 = np.random.normal(loc=[0, 3], scale=0.5, size=(num_samples_per_class, 2))
labels2 = np.ones(num_samples_per_class, dtype=np.int64) * 2

# 合并数据并划分训练/测试集（8:2）
all_data = np.vstack([class0, class1, class2])
all_labels = np.hstack([labels0, labels1, labels2])

# 打乱数据
shuffle_idx = np.random.permutation(len(all_data))
all_data = all_data[shuffle_idx]
all_labels = all_labels[shuffle_idx]

# 划分训练集（80%）和测试集（20%）
split_idx = int(len(all_data) * 0.8)
train_data = all_data[:split_idx]
train_labels = all_labels[:split_idx]
test_data = all_data[split_idx:]
test_labels = all_labels[split_idx:]

# 转换为PyTorch张量
train_data_tensor = torch.tensor(train_data, dtype=torch.float32).to(device)
train_labels_tensor = torch.tensor(train_labels, dtype=torch.long).to(device)
test_data_tensor = torch.tensor(test_data, dtype=torch.float32).to(device)
test_labels_tensor = torch.tensor(test_labels, dtype=torch.long).to(device)

# 构建DataLoader（和原代码逻辑一致）
train_dataset = TensorDataset(train_data_tensor, train_labels_tensor)
test_dataset = TensorDataset(test_data_tensor, test_labels_tensor)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)


# 3. 定义全连接网络
class FCN(nn.Module):
    def __init__(self):
        super(FCN, self).__init__()
        # 输入维度：2（二维数据），输出维度：3（3类分类）
        self.layers = nn.Sequential(
            nn.Linear(2, 64),  # 输入层：2维 → 隐藏层1：64维
            nn.ReLU(),  # 激活函数
            nn.Linear(64, 32),  # 隐藏层2：64维 → 32维
            nn.ReLU(),  # 激活函数
            nn.Linear(32, 3),  # 输出层：32维 → 3类
            nn.Softmax(dim=1)  # 输出概率分布
        )

    def forward(self, x):
        return self.layers(x)


# 4. 初始化模型、损失函数、优化器
model = FCN().to(device)
criterion = nn.CrossEntropyLoss()  # 多分类损失函数
optimizer = optim.Adam(model.parameters(), lr=learning_rate)

# 5. 训练过程
train_losses = []
for epoch in range(epochs):
    model.train()
    total_loss = 0
    for batch_data, batch_labels in train_loader:
        # 前向传播
        outputs = model(batch_data)
        loss = criterion(outputs, batch_labels)

        # 反向传播+参数更新
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        total_loss += loss.item()

    avg_loss = total_loss / len(train_loader)
    train_losses.append(avg_loss)
    print(f"Epoch {epoch + 1}/{epochs}, Loss: {avg_loss:.4f}")

# 6. 测试与评估
model.eval()
correct = 0
total = 0
with torch.no_grad():  # 测试阶段禁用梯度计算
    for batch_data, batch_labels in test_loader:
        outputs = model(batch_data)
        _, predicted = torch.max(outputs.data, 1)  # 取概率最大的类别
        total += batch_labels.size(0)
        correct += (predicted == batch_labels).sum().item()

accuracy = 100 * correct / total
print(f"\n测试集准确率: {accuracy:.2f}%")

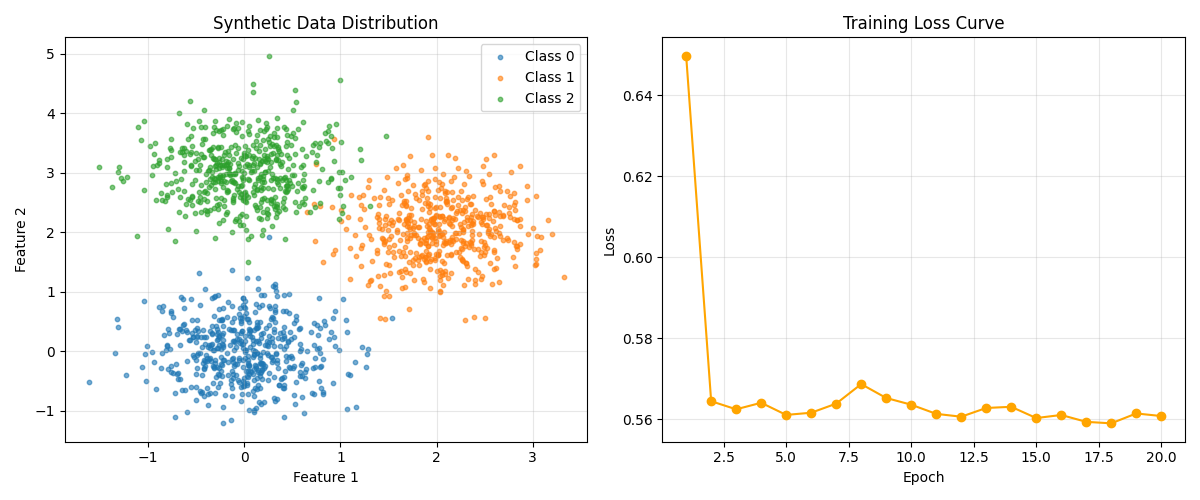
# 7. 可视化：原始数据分布 + 训练损失曲线
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

# 子图1：原始合成数据分布
ax1.scatter(class0[:, 0], class0[:, 1], label='Class 0', alpha=0.6, s=10)
ax1.scatter(class1[:, 0], class1[:, 1], label='Class 1', alpha=0.6, s=10)
ax1.scatter(class2[:, 0], class2[:, 1], label='Class 2', alpha=0.6, s=10)
ax1.set_xlabel('Feature 1')
ax1.set_ylabel('Feature 2')
ax1.set_title('Synthetic Data Distribution')
ax1.legend()
ax1.grid(alpha=0.3)

# 子图2：训练损失曲线
ax2.plot(range(1, epochs + 1), train_losses, marker='o', color='orange')
ax2.set_xlabel('Epoch')
ax2.set_ylabel('Loss')
ax2.set_title('Training Loss Curve')
ax2.grid(alpha=0.3)

plt.tight_layout()
plt.savefig('Data_Distribution_And_Training.png')
plt.show()

十、程序运行结果展示

Epoch 1/20, Loss: 0.6497

Epoch 2/20, Loss: 0.5644

Epoch 3/20, Loss: 0.5625

Epoch 4/20, Loss: 0.5641

Epoch 5/20, Loss: 0.5611

Epoch 6/20, Loss: 0.5616

Epoch 7/20, Loss: 0.5639

Epoch 8/20, Loss: 0.5687

Epoch 9/20, Loss: 0.5652

Epoch 10/20, Loss: 0.5636

Epoch 11/20, Loss: 0.5613

Epoch 12/20, Loss: 0.5606

Epoch 13/20, Loss: 0.5628

Epoch 14/20, Loss: 0.5631

Epoch 15/20, Loss: 0.5603

Epoch 16/20, Loss: 0.5611

Epoch 17/20, Loss: 0.5594

Epoch 18/20, Loss: 0.5590

Epoch 19/20, Loss: 0.5614

Epoch 20/20, Loss: 0.5608

测试集准确率: 98.00%

十一、总结

本文系统介绍了人工神经网络(ANN)的核心原理与实现。ANN通过模拟生物神经元的"加权求和+激活函数"机制实现非线性映射，具有强大的特征学习能力。文章详细解析了网络结构（输入层、隐藏层、输出层）、关键组件（权重、偏置、激活函数）以及训练机制（前向传播/反向传播）。同时提供了基于PyTorch的完整实现代码，包括数据生成、网络构建、训练和评估过程。实验结果显示，该模型在合成数据集上达到98%的准确率。最后讨论了ANN在CV、NLP等领域的应用优势，以及可解释性、数据依赖等挑战，并展望了小样本学习、多模态融合等未来趋势。