在牛顿的时代,科学家认为世界是确定 的:只要知道初始状态和力学定律,就能预测未来的一切。
但在量子力学和混沌理论诞生后,我们意识到:随机性 (Randomness) 才是世界的本质。
概率论,就是量化不确定性 的语言。
无论你是做光学仿真(蒙特卡洛光线追踪)、信号处理(卡尔曼滤波),还是量化交易(风险控制),概率论都是你无法绕开的底层代码。
今天,我们通过直觉和物理背景,重构概率论的知识体系。
01. 舞台上的主角:随机变量 (Random Variable)
概率论研究的不是具体的"数值",而是"函数"。
随机变量 (XXX) 本质上是一个函数,它把随机实验的结果映射到一个实数上。
1. 离散型 (Discrete)
- 特点:取值是可数的(一个个点)。
- 例子:抛硬币(0或1)、探测器接收到的光子数(0, 1, 2...)。
- 描述工具 :概率质量函数 (PMF) 。
P(X=k)P(X=k)P(X=k)
2. 连续型 (Continuous)
- 特点:取值是不可数的(一段区间)。
- 例子:电压噪声、加工误差、激光束的强度分布。
- 描述工具 :概率密度函数 (PDF) 。
f(x)f(x)f(x)
⚠️ 关键误区 :
对于连续变量,f(x)f(x)f(x) 不是 概率!
f(x)f(x)f(x) 可以大于 1。只有对它进行积分(面积),得到的才是概率。单点 P(X=x)P(X=x)P(X=x) 的概率永远是 0。
02. 描述形状的工具:PDF 与 CDF
概率密度函数 (PDF, f(x)f(x)f(x))
它描述了随机变量在某一点附近的"密集程度"。
- 性质 :全积分等于 1。
∫−∞∞f(x)dx=1\int_{-\infty}^{\infty} f(x) dx = 1∫−∞∞f(x)dx=1
累积分布函数 (CDF, F(x)F(x)F(x))
它描述了"小于等于某个值"的概率。
F(x)=P(X≤x)=∫−∞xf(t)dtF(x) = P(X \le x) = \int_{-\infty}^{x} f(t) dtF(x)=P(X≤x)=∫−∞xf(t)dt
- 物理意义:如果你在做良率分析,CDF 告诉你"有多少比例的产品是合格的"。
- 关系:PDF 是 CDF 的导数。
03. 描述特征的数字:期望与方差
如果我们不想看整张图,只想用两个数来概括这个分布:
1. 期望 (Expectation, μ\muμ) ------ 重心
E[X]=∫xf(x)dxE[X] = \int x f(x) dxE[X]=∫xf(x)dx
- 直觉:如果你重复无数次实验,平均值会收敛到这里。它是分布的"物理重心"。
2. 方差 (Variance, σ2\sigma^2σ2) ------ 惯性矩
Var(X)=E[(X−μ)2]Var(X) = E[(X - \mu)^2]Var(X)=E[(X−μ)2]
- 直觉:数据偏离中心的程度。
- 物理意义 :
- 在信号处理中,方差代表交流功率 (AC Power) 或 噪声强度。
- 在金融中,方差代表风险 (Volatility)。
- 在光学中,方差对应光斑的宽度平方。
04. 工程师必须认识的"动物园"
在无数种分布中,这三种支配了物理世界:
1. 伯努利/二项分布 (Binomial)
- 场景 :抛硬币。做 nnn 次实验,成功 kkk 次。
- 公式 :P(k)=Cnkpk(1−p)n−kP(k) = C_n^k p^k (1-p)^{n-k}P(k)=Cnkpk(1−p)n−k
2. 泊松分布 (Poisson) ------ 光学人的老朋友
- 场景 :稀有事件在固定时间/空间内发生的次数。
- 光学应用 :散粒噪声 (Shot Noise) 。
- 光子是一粒一粒到达探测器的。即使激光功率恒定,单位时间内到达的光子数 NNN 也服从泊松分布。
- 特征 :方差 = 期望 (σ2=μ\sigma^2 = \muσ2=μ)。这意味着光越强,噪声的绝对值越大(σ=N\sigma = \sqrt{N}σ=N )。
- 公式 :P(k)=λke−λk!P(k) = \frac{\lambda^k e^{-\lambda}}{k!}P(k)=k!λke−λ
3. 正态分布 / 高斯分布 (Normal / Gaussian)
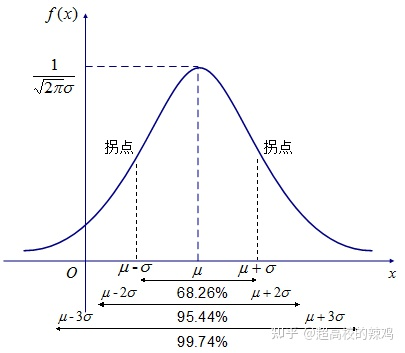
- 场景 :误差、热噪声。
- 光学应用:高斯光束的横向电场分布、光谱线的Doppler展宽。
- 公式 :
f(x)=12πσe−(x−μ)22σ2f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=2π σ1e−2σ2(x−μ)2 - 68-95-99.7 法则 :
- ±1σ\pm 1\sigma±1σ 包含 68% 的数据。
- ±2σ\pm 2\sigma±2σ 包含 95% 的数据(常用的置信区间)。
- ±3σ\pm 3\sigma±3σ 包含 99.7% 的数据(良率标准)。
05. 两大定海神针:极限定理
为什么正态分布如此重要?因为有下面这两个定理撑腰。
1. 大数定律 (Law of Large Numbers, LLN)
- 含义 :频率收敛于概率。
- 只要实验次数 nnn 足够多,样本均值 Xˉ\bar{X}Xˉ 一定会无限接近真实期望 μ\muμ。
- 应用 :这是蒙特卡洛仿真 (Monte Carlo Simulation) 的理论基础。你在 TracePro/LightTools 里追迹 100 万条光线来模拟照度,就是靠它保证结果准确的。
2. 中心极限定理 (Central Limit Theorem, CLT) ------ 概率论的王冠
- 含义 :从任意分布中抽取样本,只要样本量足够大,样本均值的分布近似于正态分布。
- 直觉 :不管原本的变量是三角分布、均匀分布还是奇形怪状的分布,只要它们是独立同分布 (i.i.d) 的,把它们加起来(或取平均),结果就是高斯分布。
- 物理启示 :
- 为什么测量误差通常是正态的?因为误差是由无数个微小的、独立的干扰因素(温度波动、震动、电子热运动)叠加而成的。根据 CLT,叠加的结果必然趋向正态。
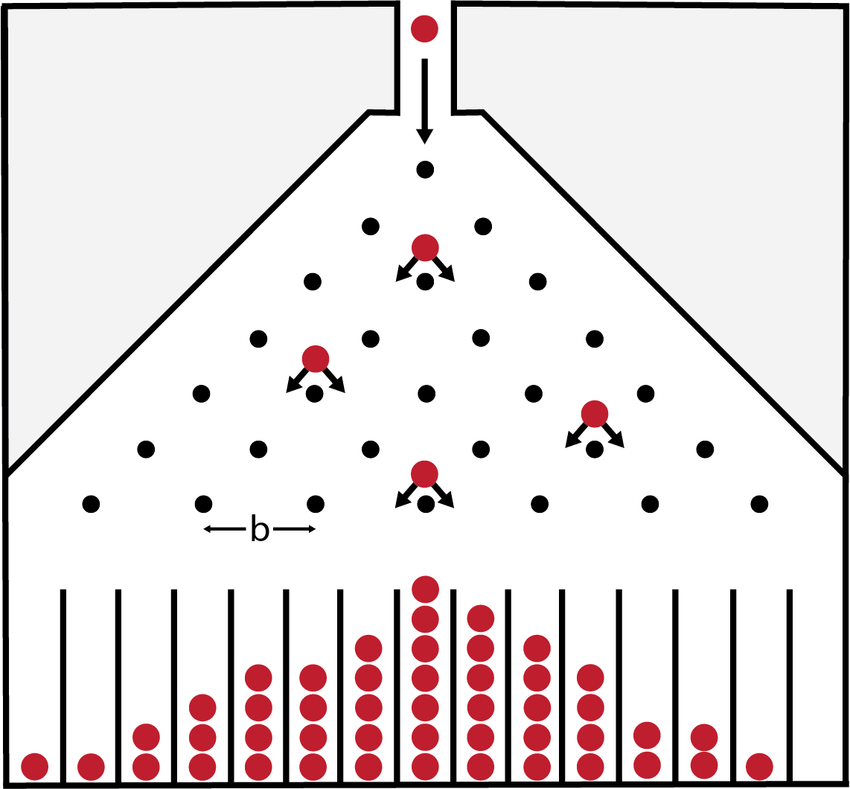
(图注:高尔顿板。小球经过层层钉子的随机碰撞(独立事件叠加),最终在底部堆积成完美的正态分布曲线。)
06. 总结
- 随机变量是把世界数字化的函数。
- PDF/CDF 是描述不确定性形状的工具。
- 泊松分布支配着量子化的光子(散粒噪声)。
- 正态分布支配着宏观的误差(热噪声)。
- 中心极限定理告诉我们:在混沌的随机叠加中,最终会涌现出完美的秩序(高斯曲线)。
理解了这些,你再看光学探测器的信噪比公式,或者卡尔曼滤波的协方差矩阵,就会发现它们不再是冷冰冰的数字,而是描述世界运行规律的诗篇。