第一章
算法复杂度分析
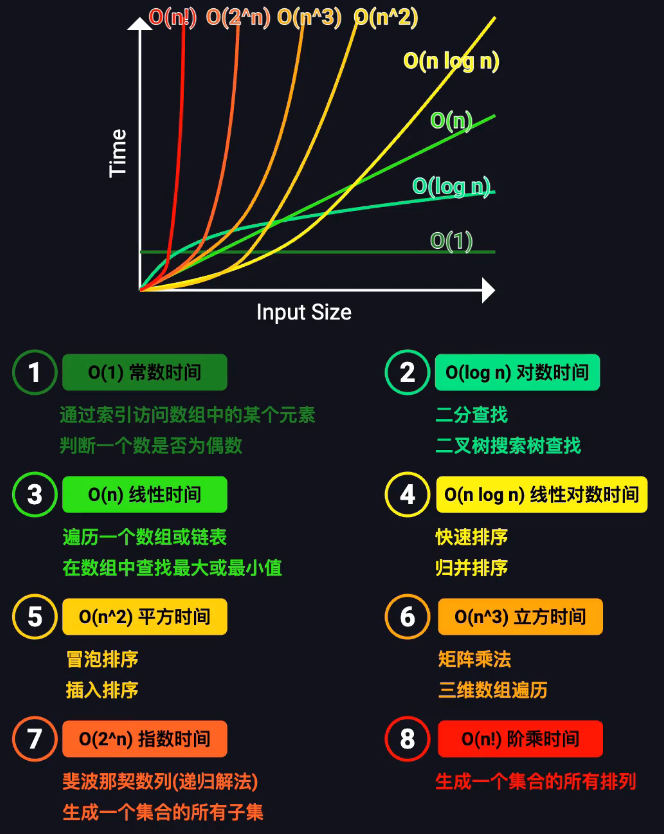
性质:
消常
消非主导项
幂集问题
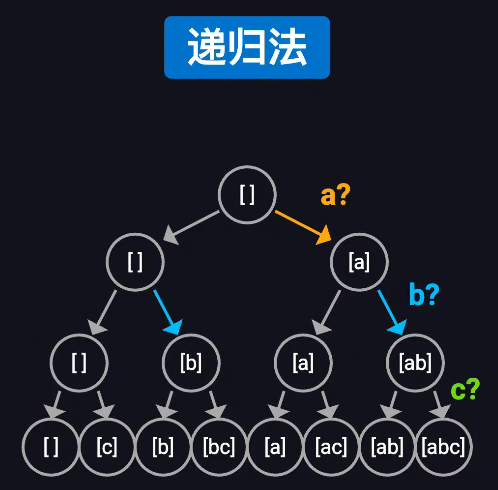
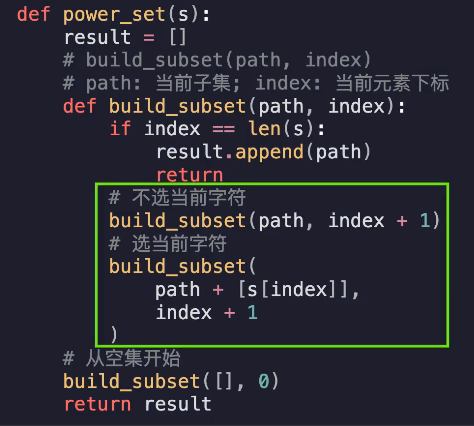

时间复杂度:O(2^n)
链表与数组(公式化描述)
1. 公式化描述(顺序存储 / 数组)
- 所有元素连续存放在内存中。
- 假设每个元素占
sizeof(int)空间(比如 4 字节),共 9 个元素。 - 总空间 =
n × sizeof(element)=9 × 4 = 36字节
2. 链表描述(链式存储 / 单链表)
- 每个节点包含:数据域 + 指针域
- 数据域:存一个整数(4 字节)
- 指针域:存下一个节点的地址(通常 8 字节,64位系统)
总空间 = 9×12=108 字节
链表反转
【3分钟搞懂链表反转 | 链表面试题】 https://www.bilibili.com/video/BV1SCtBzyESd/?share_source=copy_web\&vd_source=2c56c6a2645587b49d62e5b12b253dca
三指针法
Pre先指向none,先将Next(指针)标记为下一个节点,然后把当前节点的next(属性)设置为前一个节点Pre(此时已经断开连接),然后推进Cur到Next,因为虽然断了连接,但是Next却保存着下一个节点的信息,因此仍然可以正常推进Cur和Pre迁移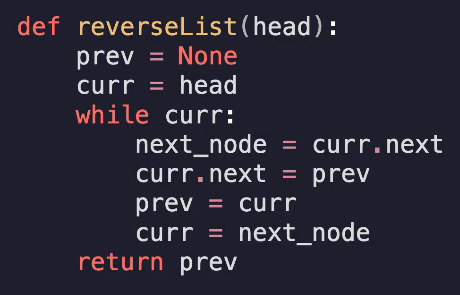
时间复杂度O(n) 每个节点都会被访问一次
第二章
二分查找
必须是数组 必须有序


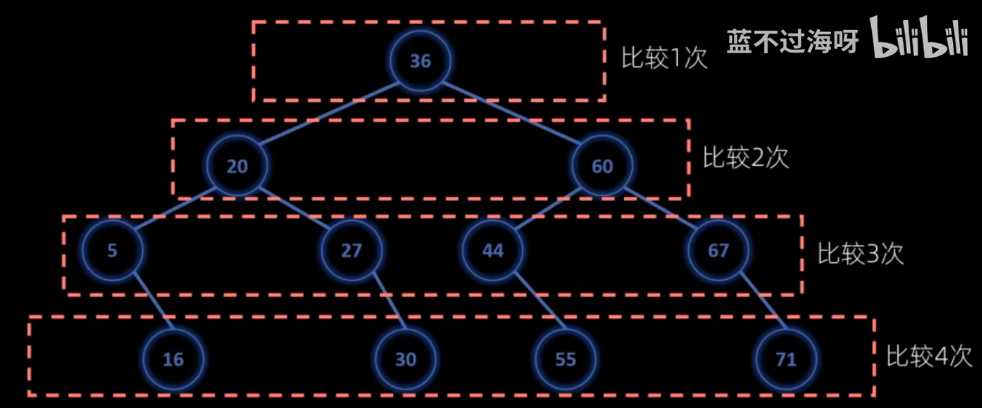
时间复杂度:O(logn)
ASL------平均查找长度
ASL成功=每一层层数*每一层个数/n
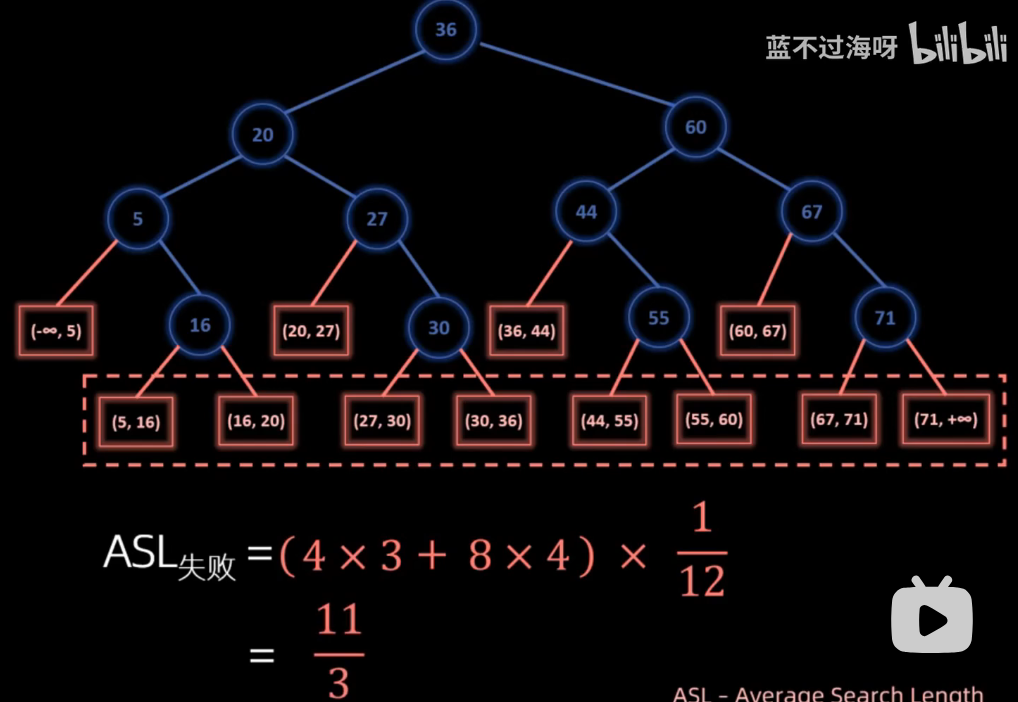
ASL失败=Σ第n层失败节点数*(n-1)
冒泡排序
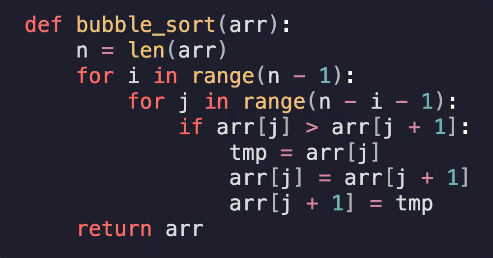
时间复杂度:O(n^2)
插入排序
将数组分为已排序和未排序两部分
依次从未排序中取出一个元素,放入已排序中
就是打牌


时间复杂度:O(n)~O(n^2)
空间复杂度:O(1)
选择排序
从未排序区找最小元素,和当前元素交换(双指针,当min≠i时即替换并i++)
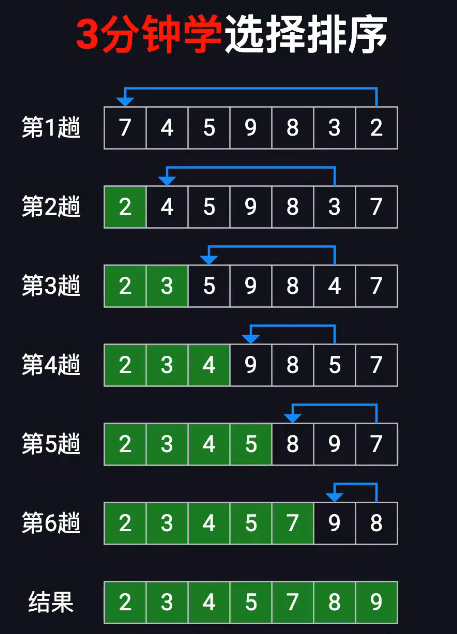
时间复杂度:O(n^2) 扫描n n轮
空间复杂度:O(1)
堆排序
建堆
排序:将最大元素取出,将最小元素替换上去(利用删除的性质)

算法复杂度:
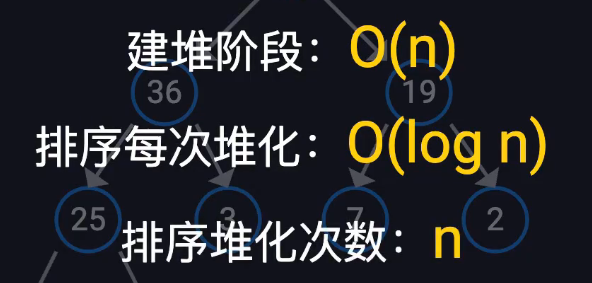
空间复杂度O(1)
前后缀表达式计算

中缀转前后缀表达式
1.加括号,对每一次运算都加括号
2.将运算符挪到括号左边
第六章
链表插入
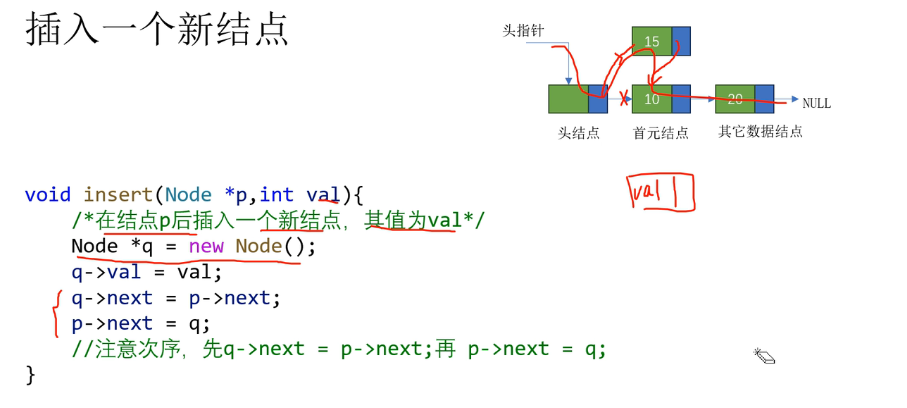


第八章
汉诺塔的递归解决
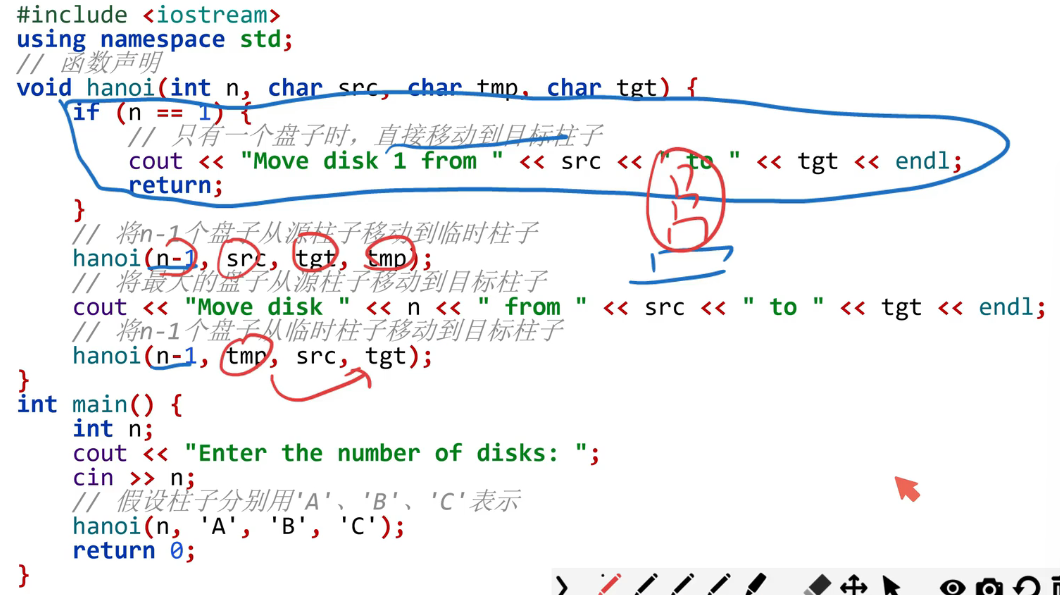
第十章
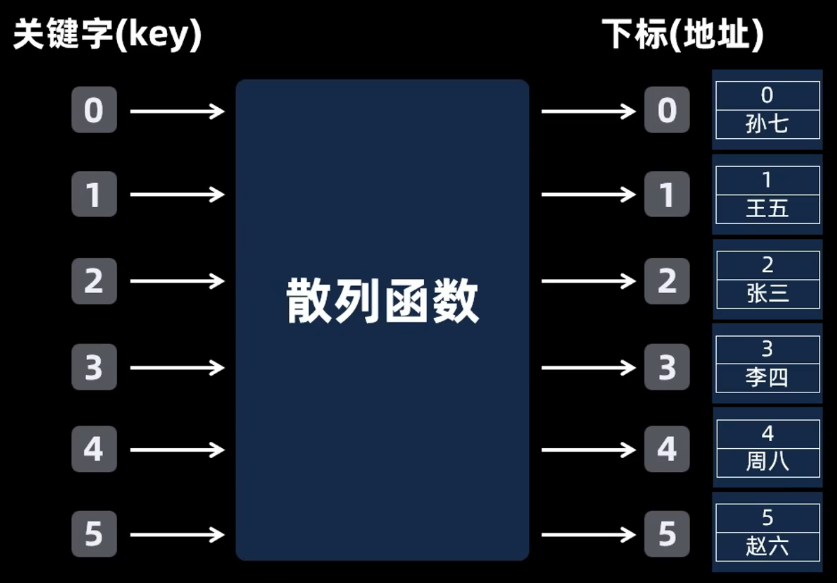
散列 哈希表
构建下标和关键字的关系,比如一一对应,此时的查找效率O(1)
H(key)=key
但这个散列函数不固定
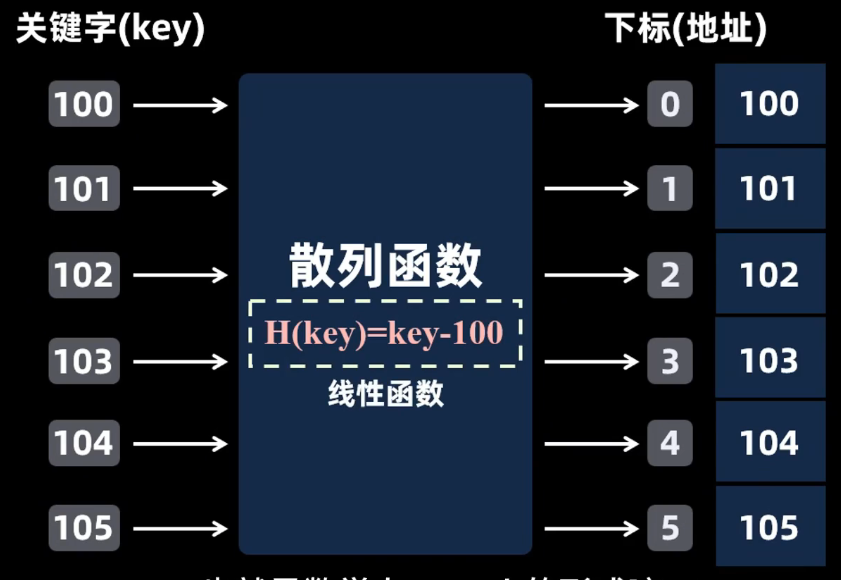
直接定址法------关键字连续的
可用通过调整下标b来把映射地址调整为从0开始
除留余数法------分散列
让关键字对某个数p求余数,使得不连续的关键字映射到连续的哈希表上
p一般去小于等于表长的最大质数

散列表的冲突 与 效率
同义词------两个映射到同一块散列表地址上了
1.散列函数的选取
直接定制法:浪费但不冲突
除留余数法:不浪费但冲突
2.装填因子/散列表的空间利用率α

越大则碰撞概率越大
3.处理冲突的方式(重点)
开放定址法:找新的空间存放同义词
线性探测法:依次查找后一个位置
存储/插入阶段
空位置和带有DEL的位置都可以插入


查找阶段
先找对应下标的位置,如果不一致就线性向后探测
ASL------平均查找长度
由于冲突存在,在查找中进行了多次比较,可用使用ASL 平均查找长度 来衡量散列表的效率
对于单个查找数字,其查找长度=真实位置-映射位置
ASL成功=Σ所有关键字的查找长度/n (关键字数量)

ASL失败=Σ所有关键字到空位置的距离(映射到这里直到查找失败比较了几次)(mod数)
切记任何关键字都不可能映射到下标11的,因为在mod数外

删除阶段
使用DEL=-1进行占位,不能直接删除 否则线性搜索会被截断!!!

平方探测法

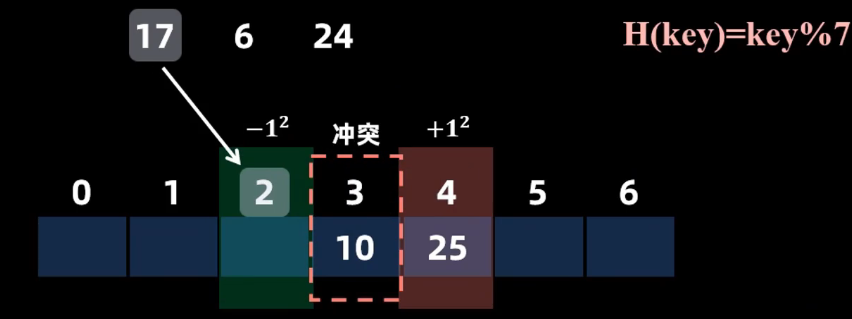

拉链法
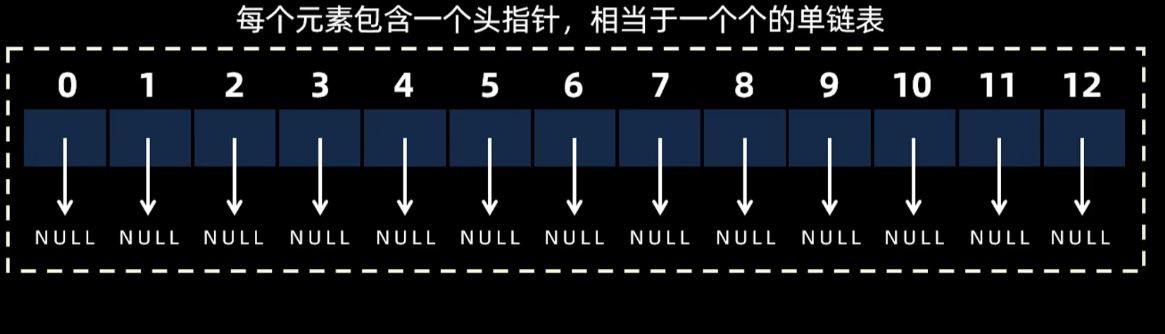
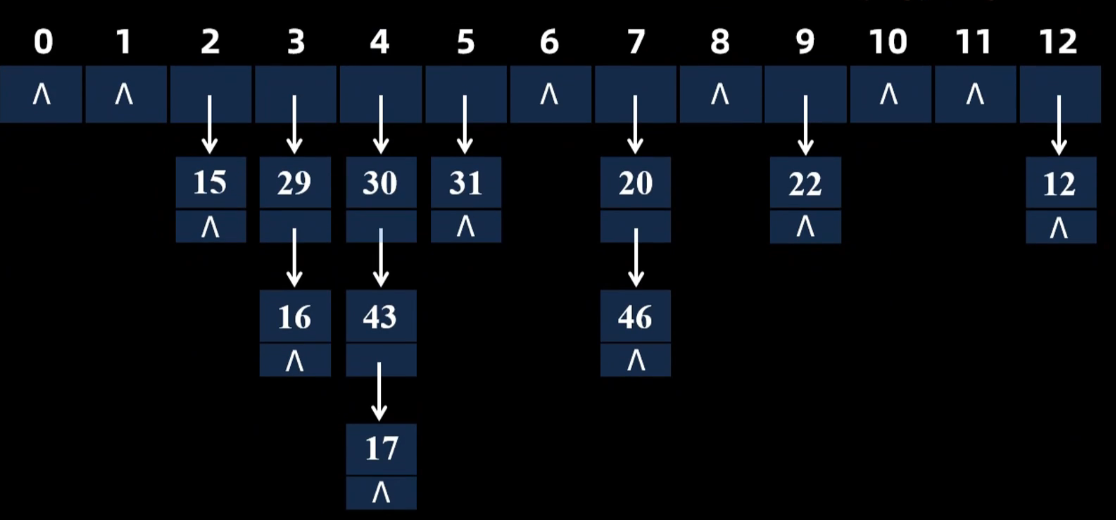
计算性能
ASL成功=第一层*1 + 第二层*2 + 第n层*n /n
ASL失败=11(关键字个数)/13(链表长度)
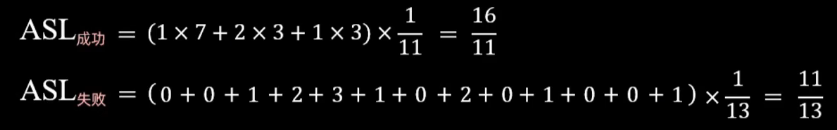
可以直接删除
第十二章 堆------用于找最大最小值
用于动态保存当前可用选择的边,最好是取出最大最下作为下一次使用的情况,比如Prim算法每次都需要从最小堆中招找权重最小的边进行添加
堆的定义
基于完全二叉树,除了最后一层都是满的,最后一层做连续排列
堆序性:最大最小堆
堆的特性
插入 删除 排序都是logn 建堆是n

堆的高度:logn
堆的数组表示与索引关系
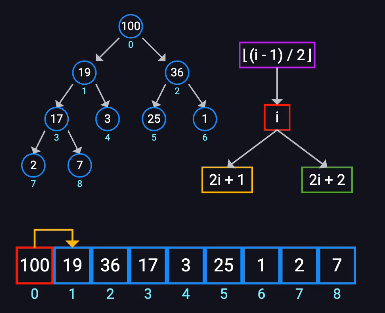
堆的插入
在已经建好的堆中插入一个节点
- 将新元素插入到堆的末尾(插入)
2.从新元素上浮交换,直到满足堆的性质(调整)
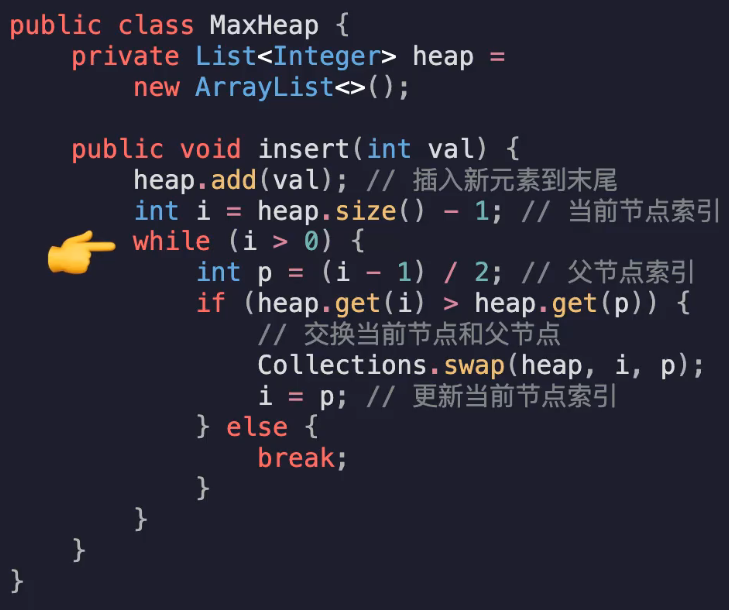
创建heap数组,往最后一个位置插入新元素
确认新节点的位置i=heap.size()-1
当i没有到根节点前都执行循环,
找到父节点p=(i-1)/2,比较二者大小
比p大就交换,更新新位置i=p
比p小就跳出break
时间复杂度:要把末尾元素上浮要执行高度次 即O(logn)
堆的删除
1.移除堆顶元素,用堆中最后一个元素替代堆顶
2.通过下沉,对比当前节点与子节点大小,交换
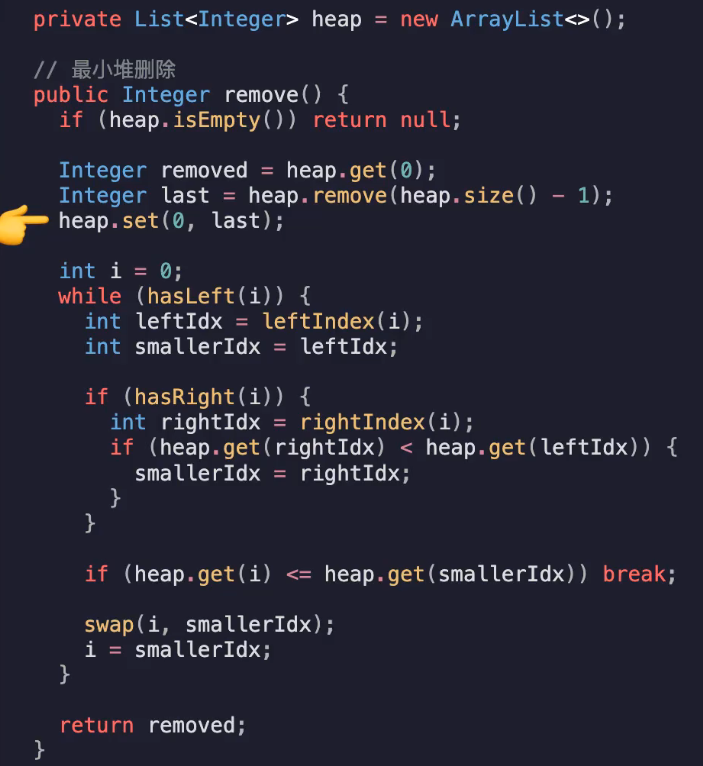

创建队列heap
首先保存堆顶元素heap.get(0),这是作为返回值的
然后交换last和0元素
接着从头i=0开始下沉:
如果有左节点就设左节点更小,如果还有右节点就要对比左右节点谁更小
如果有小的就swap,同时设置i为小节点的idx
直到左右节点小的那个值比当前get(i)的值更大,跳出break
时间复杂度:同理O(logn)
堆的构建
将一个无序数组转为符合堆的数组结构
从最后一个非叶子节点开始调整
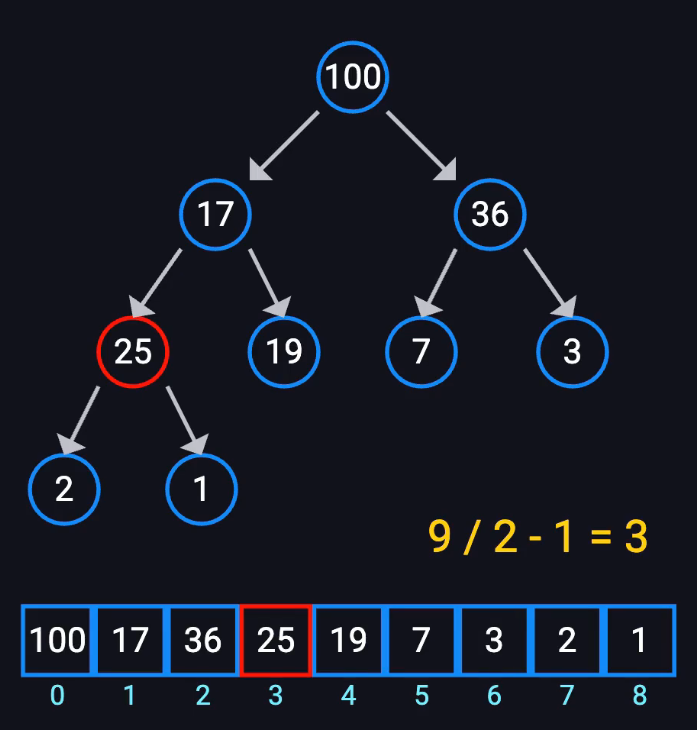
最后一个非叶子节点的下标是:len/2-1

从最后一个非叶子节点向前堆化
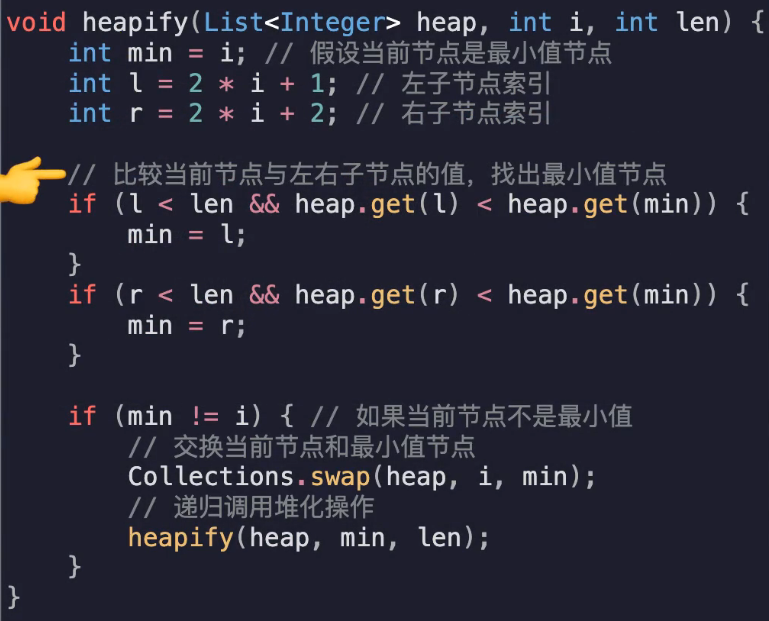
对于当前i节点,对比其左右子节点,2i+1/2,如果存且比当前i更小则设置min=l/r
如果min不是i则证明被替换了,执行swap
然后递归调用堆化
时间复杂度:O(n)
哈夫曼树与哈夫曼编码
非歧义且最短
1.统计出现的次数
2.定义节点和值,值是其出现的次数
3.每次合并最小的两个
4.左0右1

让出现次数越多的编码越短。由于都是叶子节点,因此不在另一个节点的路上,不会重复
带权路径长度=路径长度*叶子节点权重
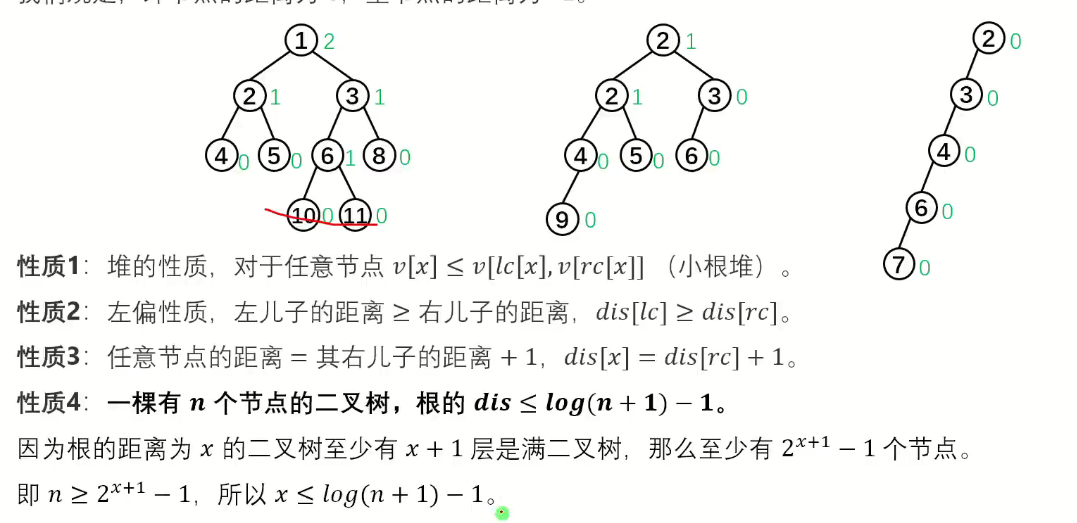
左高树/左偏树
【C16【模板】左偏树(可并堆)】 https://www.bilibili.com/video/BV1Hz4y177gn/?share_source=copy_web\&vd_source=2c56c6a2645587b49d62e5b12b253dca
左偏树(Leftist Tree,又称左偏堆)是一种可合并堆(Mergeable Heap) ,主要用于高效地合并两个优先队列 。它与二叉搜索树(BST)、AVL 树、红黑树虽然都是树形数据结构,但设计目标、性质和应用场景完全不同。
性质
合并
先拆解比较 到空为止 再合并,合并过程中如果左小于右则交换左右子树
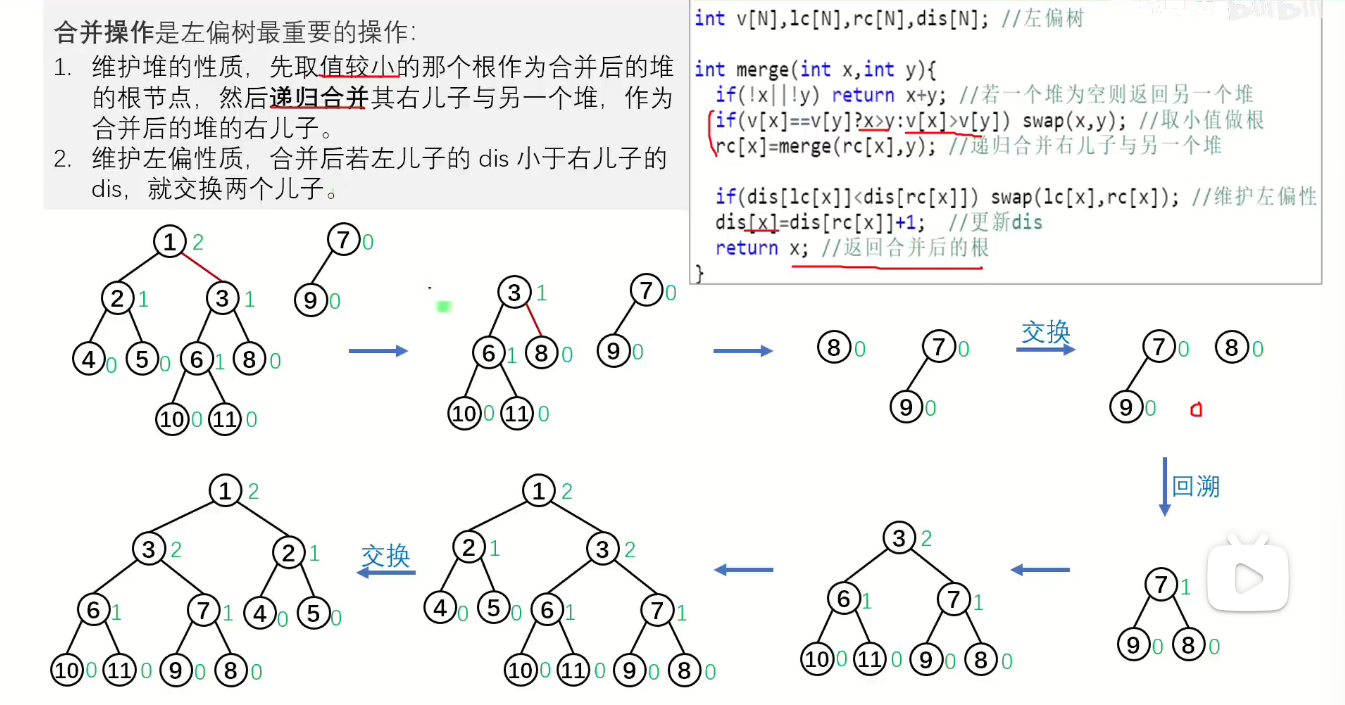
时间复杂度:

第十四 十五章------树
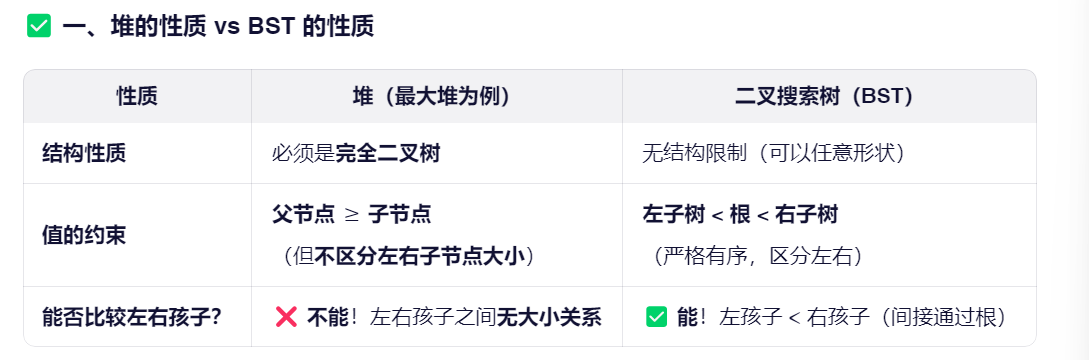
堆只管"上下级"(父子),
BST 还管"左右派"(左右子树顺序)。因此堆的调整只需要通过上浮和下沉即可,而二叉搜索树、红黑树、AVL都需要旋转才行!!!
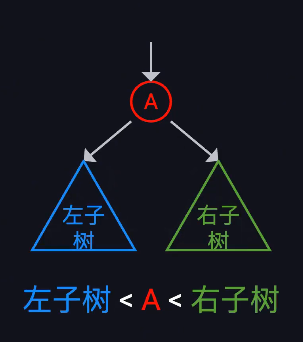
二叉搜索树

任何节点都有当前值、左右节点三个属性
二叉搜索树则拥有这个节点属性,同时也有增删改查几个方法
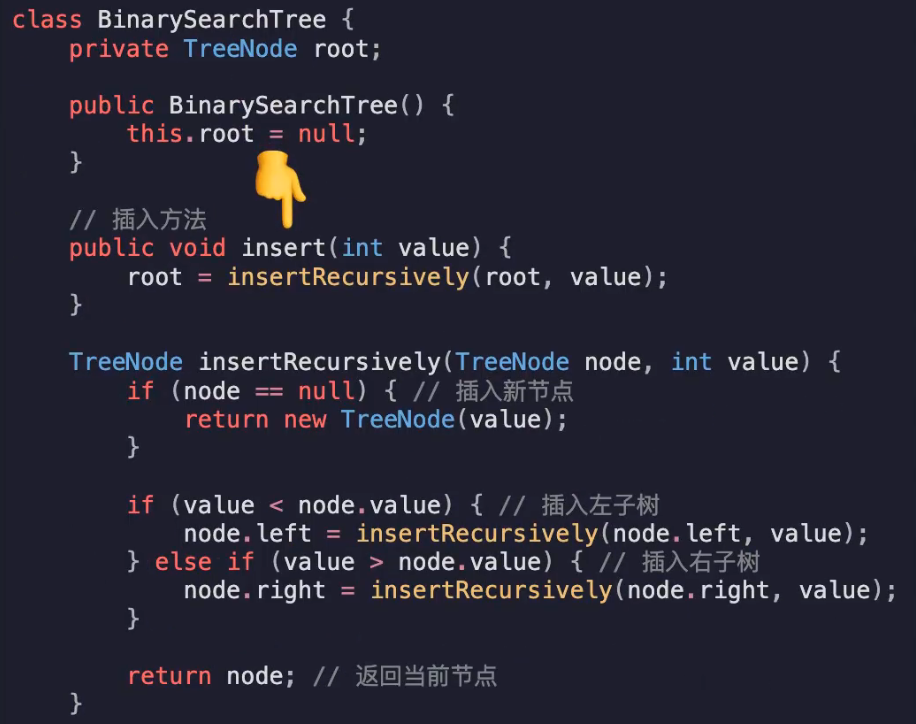
如果没有根就是根,通过new创建新TreeNOde
如果有则判断当前值与左右节点node.value
如果大于则insert右子树,小于则insert左子树
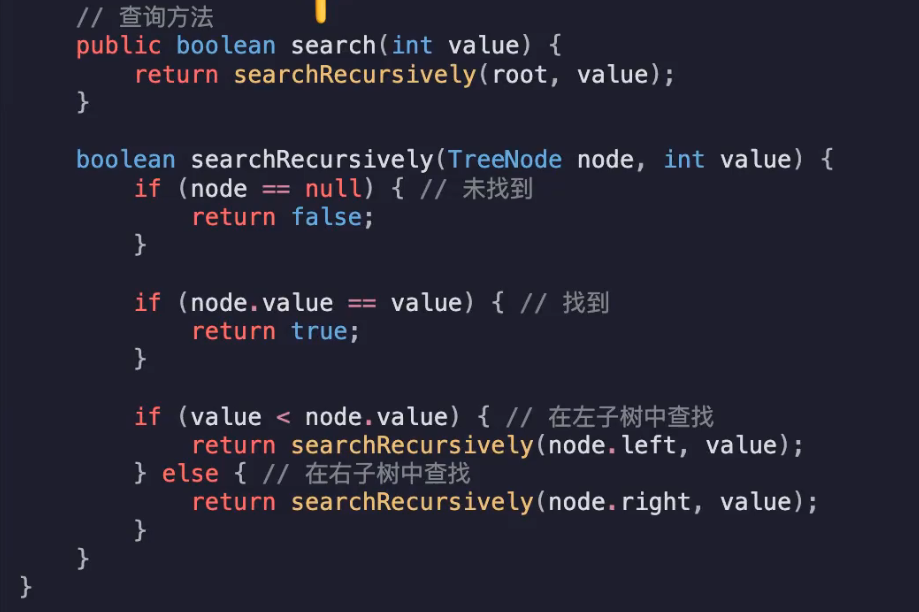
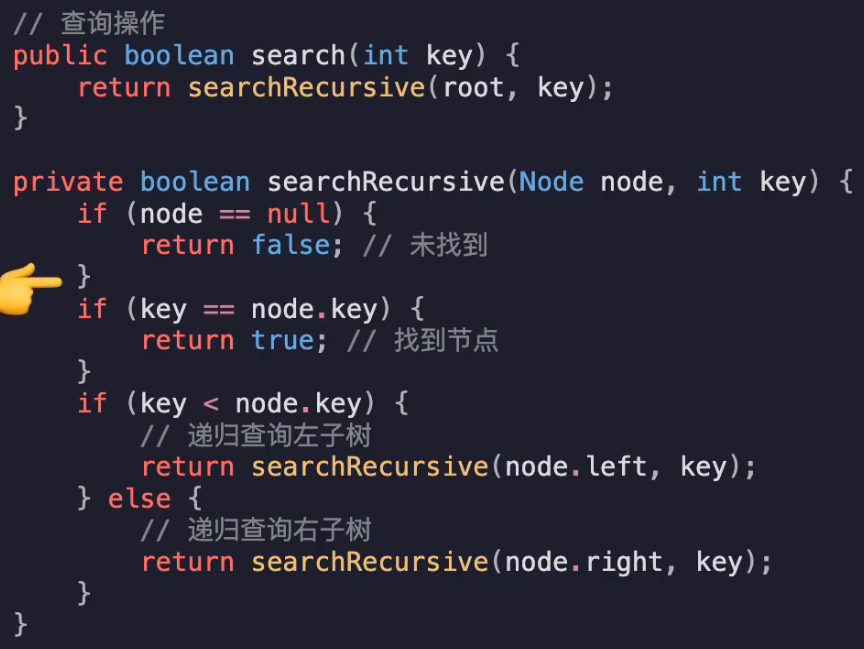
查找类似,如果当前值比node.value小则在左子树查,直到找到或查到叶子节点node==null的情况
插入 查找 删除的时间复杂度:O(logn)
极端情况下退化为O(n)
二叉搜索树的删除
删除叶子节点------直接让父节点的左右指针指向null
删除只有一个叶子节点的父节点------让父节点的单侧指针指向这个节点唯一连着的那个节点
删除有两个叶子节点的父节点

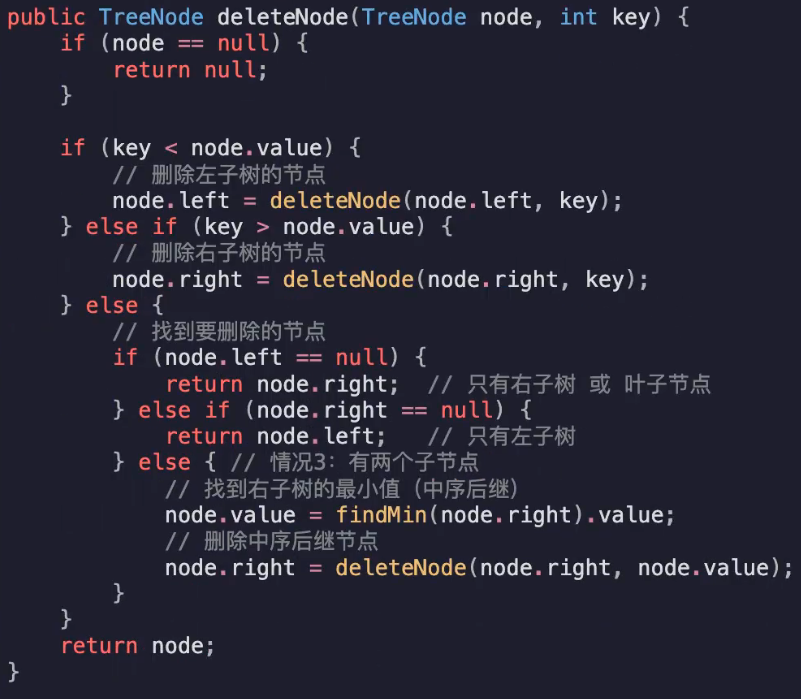
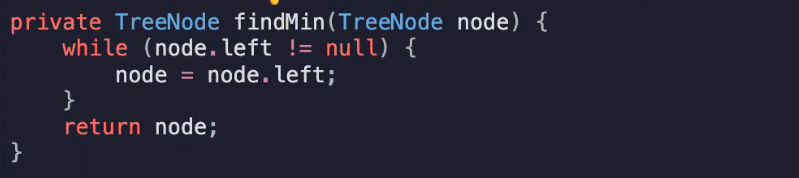
先找到要删除的节点key,递归调用
找到后执行删除
如果左子树或右子树不存在或都不存在,就直接返回另一侧即可
如果两个自述都存在,就寻找中序后继,即右子树的最小左节点
调用在Node.right中找最小值的函数,最后删除中序后继节点
前中后序列的遍历与生成与知二推一
AVL树
普通二叉搜索树的结构会由于插入顺序的不同退化为链表
AVL通过严格平衡条件,使得树高不高,具有自平衡性
平衡因子=左子树高-右子树高
对于平衡二叉树,平衡因子的范围为[-1,0,1]也就是说,左右子树高差不超过1
可以通过旋转操作平衡
增删改查的时间复杂度:O(logn) n是节点数量
但是旋转操作非常频繁
红黑树通过堆红色节点的约束,保证最大树高不超过最小数高的两倍
因此AVL树更使用于查询密集的场景,红黑树适用于插入删除密集的场景

需要节点值、节点高度、左右子节点,节点高度用于计算平衡因子
AVL树的插入
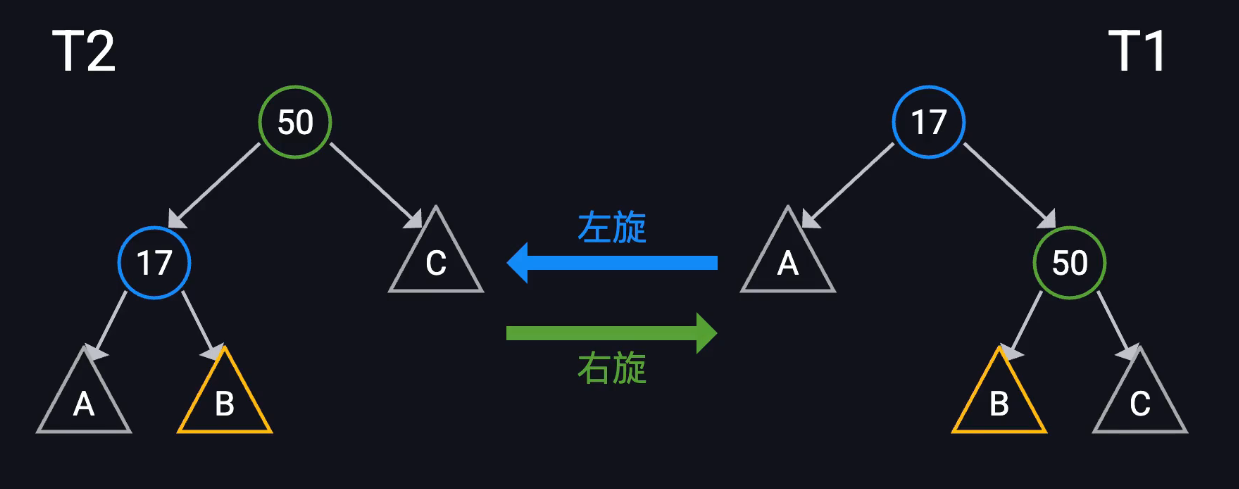
注意子树的归属!!!
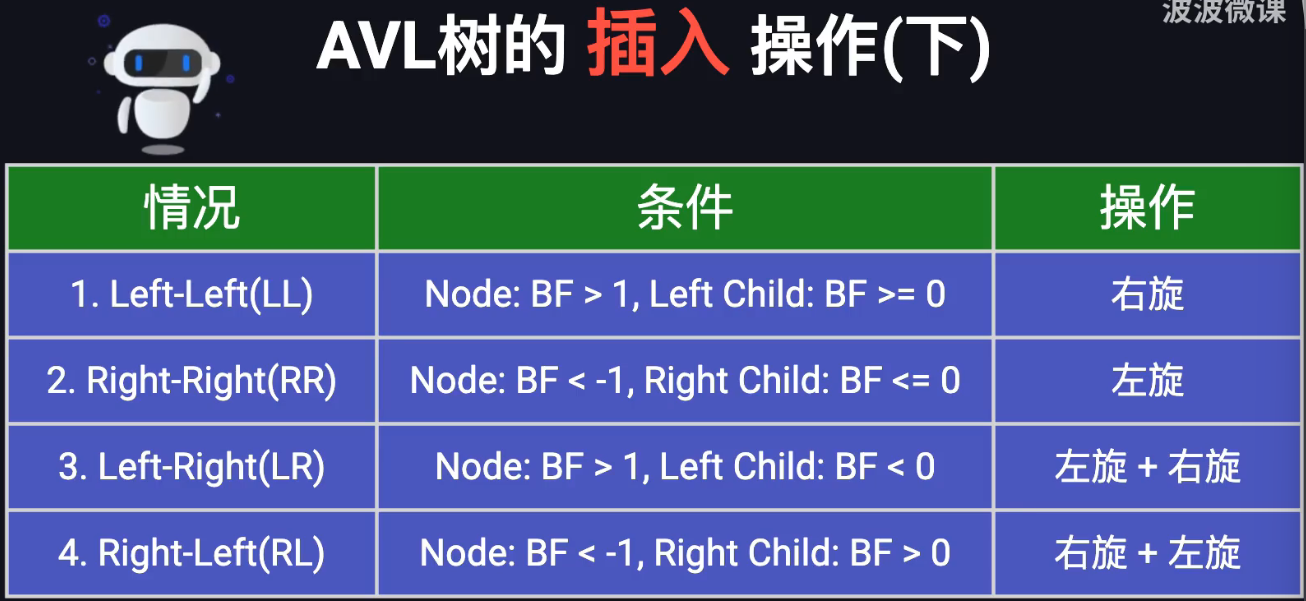
AVL树的删除
和二叉搜索树一致,但是每次删除后都需要重新平衡一次
已知前序中序求后序 已知中序后续求前序
【【有挂!!】二叉树遍历秒解,前序遍历、中序遍历、后序遍历-哔哩哔哩】 https://b23.tv/IBUkkdf
【无脑秒解!已知先/后序遍历与中序遍历,求后/先序遍历。-哔哩哔哩】 https://b23.tv/Cpvk3YR
红黑树(不考)
调整旋转次数少
约束红黑树:
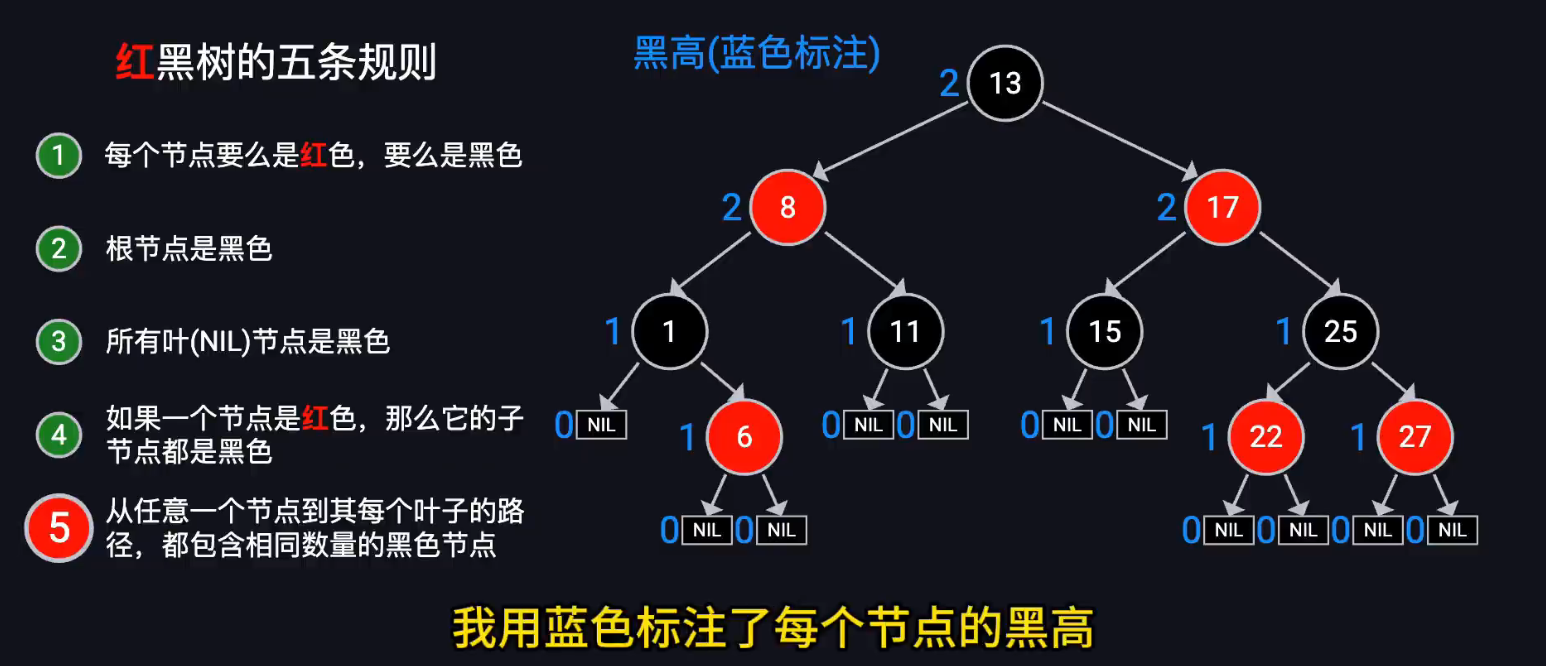
保证从根节点到叶子节点的最长路径不超过最短路径的两倍
时间复杂度:

旋转的时间复杂度是:O(1)只涉及指针的变化
红黑树的插入
1.按照二叉搜索树插入新的红色节点
2.若规则被破坏(红红冲突),通过重新着色和旋转解决
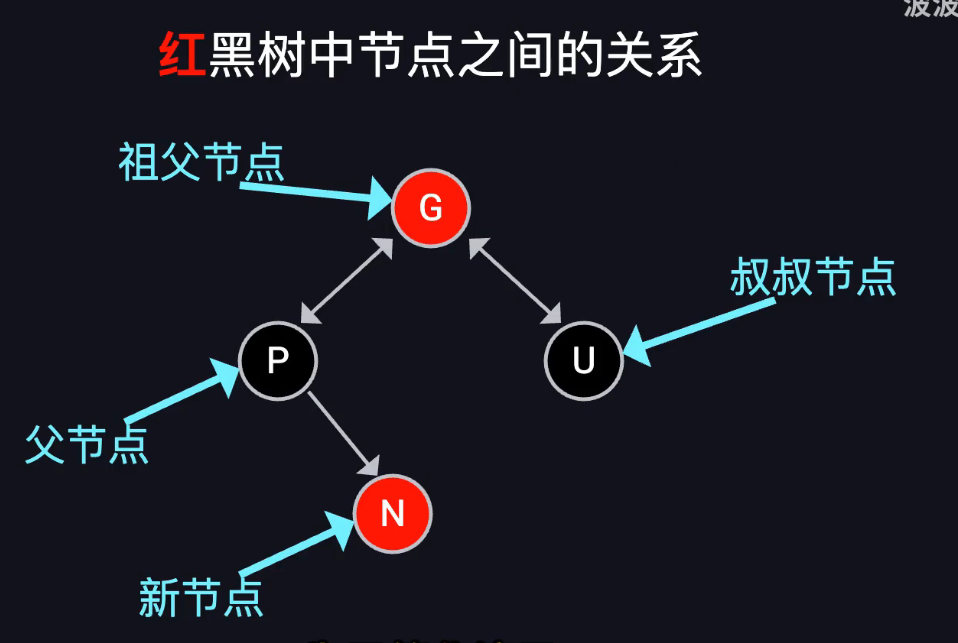
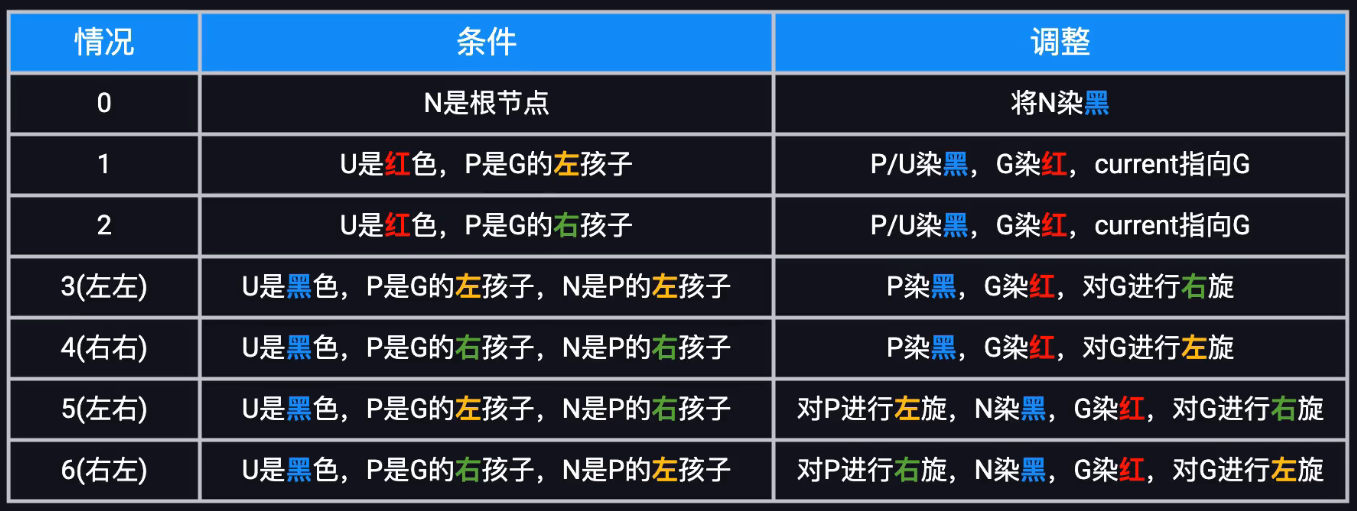
时间复杂度:查找(logn)+调整(logn)=O(logn)
B-树 多叉平衡搜索树(类似并查集的路径压缩后)
【B树(B-树) - 来由, 定义, 插入, 构建】 https://www.bilibili.com/video/BV1tJ4m1w7yR/?share_source=copy_web\&vd_source=2c56c6a2645587b49d62e5b12b253dca
用于急需要快速查找且需要保持数据的顺序
每一层都需要访问一次 因此压缩高度后访问次数就少了
读取多个字节和读取单个字节的耗时基本一样,因此一个节点多个数据是可以的
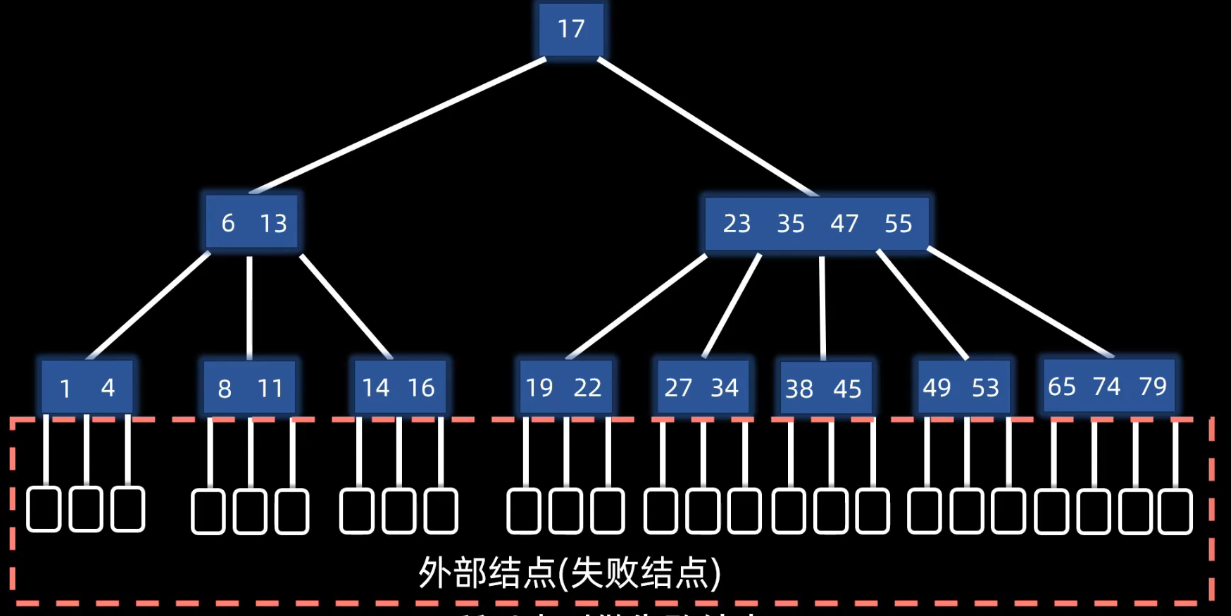
n阶B树------最大n叉
性质:
平衡:所有的叶子在同一层
有序:节点内有序 任意元素的左子树都小于他 右子树大于他
多路:m叉树
最多m个分支 节点内最多m-1个元素
根节点最少两个分支 一个元素
其他节点至少m/2个分支 m/2-1个元素
查找
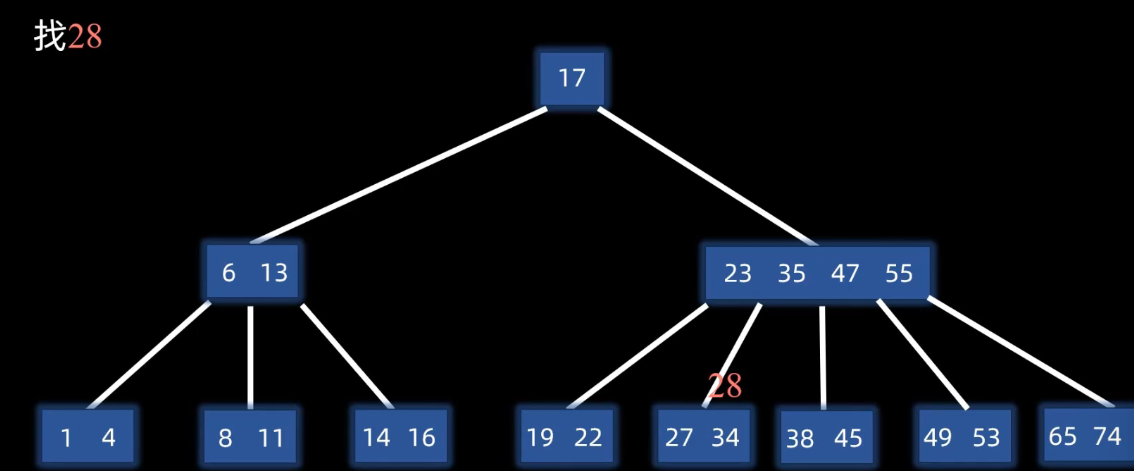
插入(满了上移中间)
插入都是在叶子节点层操作的,发送上溢出才会触发上层
插入目标节点14:
先插入到指定位置,超过m叉树定义,发生分裂:
第m/2个元素上移,其左右两个元素分裂
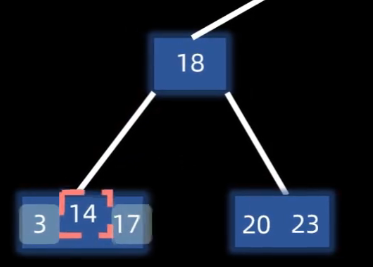
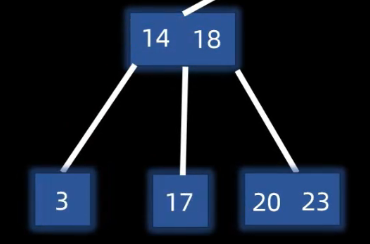
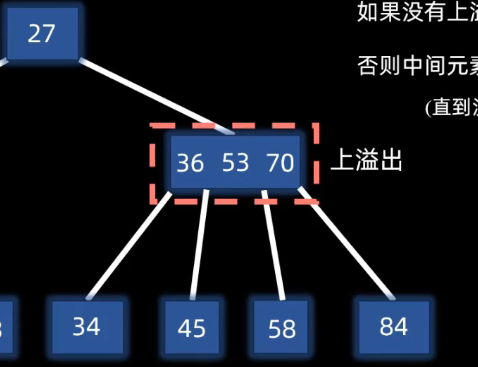
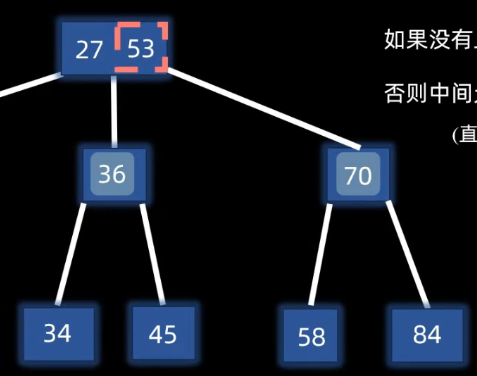
构建

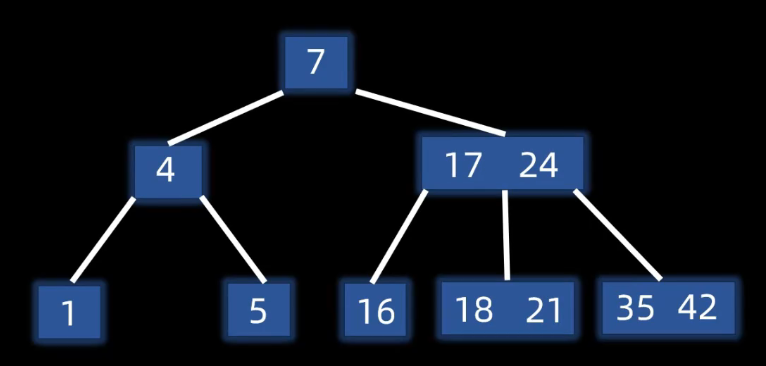
删除
对于5阶B树
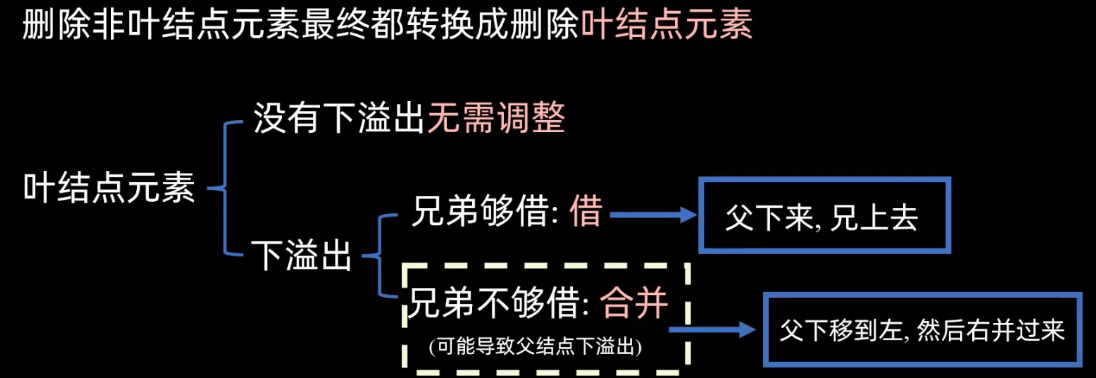
删除非叶子节点都会转换为删除叶子节点
类似AVL的删除,或堆的删除,将其直接前驱 直接后继替换后删除原指定节点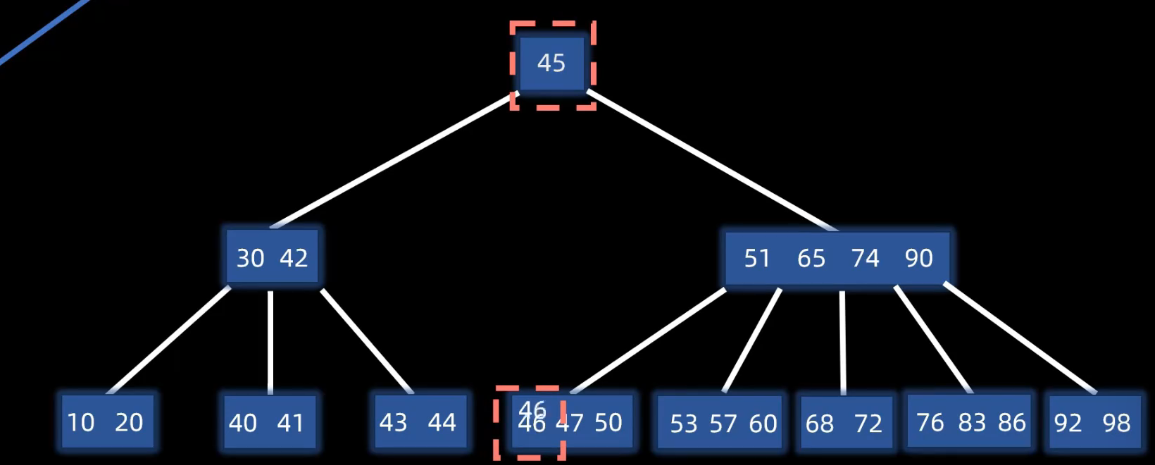
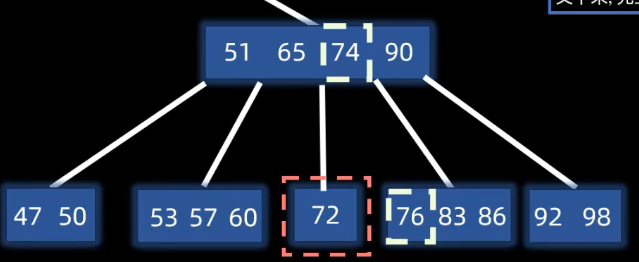
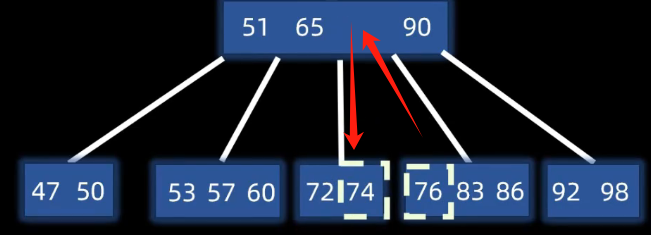
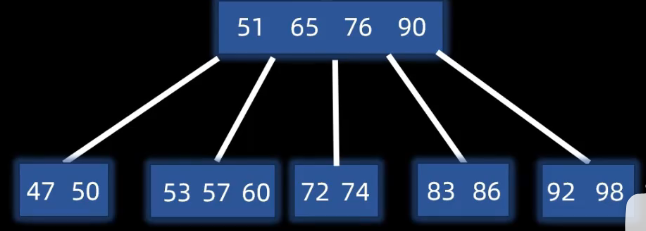
对于出现下溢出的节点(删除后节点元素少于m/2个)
则遵循父下来 兄上去,向左右节点借一个元素,因此要改变父节点,把父节点拉下来,让兄弟节点上去
第十六章
图
邻接矩阵
方便找到是否有边 顶点的度
但是空间复杂度高 对于统计边的数量只能枚举

入度:竖 出度:横
邻接表
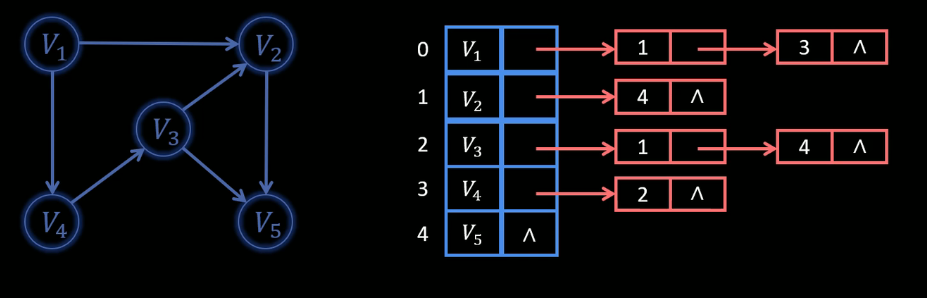
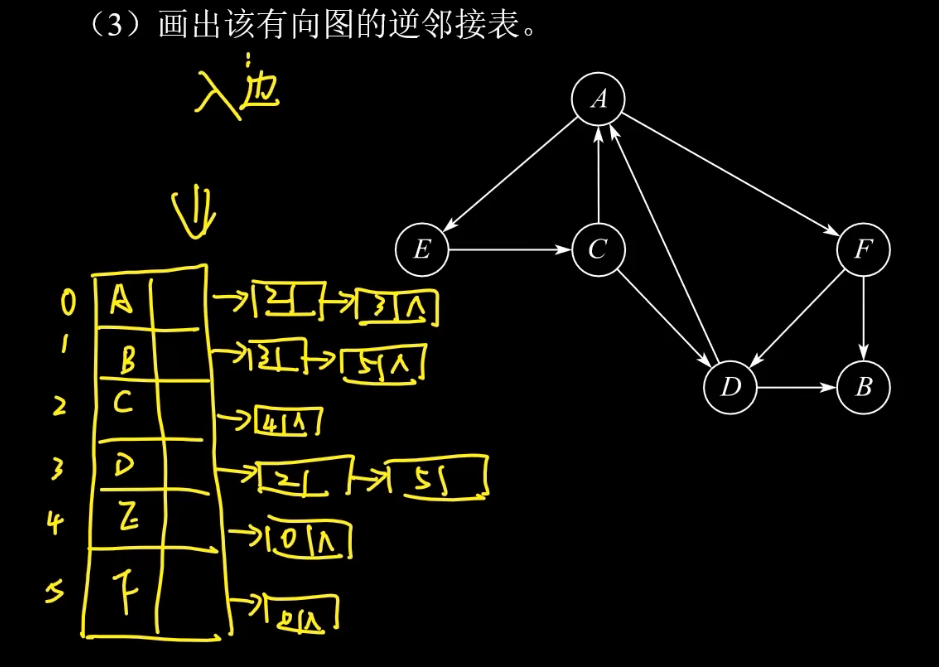
深度优先搜索 DFS
基于栈的访问
算法复杂度
时间复杂度:O(n) 每个节点都被访问
空间复杂度:最坏O(n)。AVL树O(logn)
用于生成括号-子集枚举-N皇后问题
搜索所有可能路径
广度优先搜索 BFS
基于队列的访问
先进先出-离得近的先访问
算法复杂度

空间复杂度:对于平衡二叉树,一般存入队列的是一层的内容,不超过树高logn;对于普通搜索树则是O(N)
第十九章 贪心
迪杰斯特拉算法
由于要探索最短代价的节点,每次需要从最小堆中取出堆顶元素,因此要用优先队列(堆)
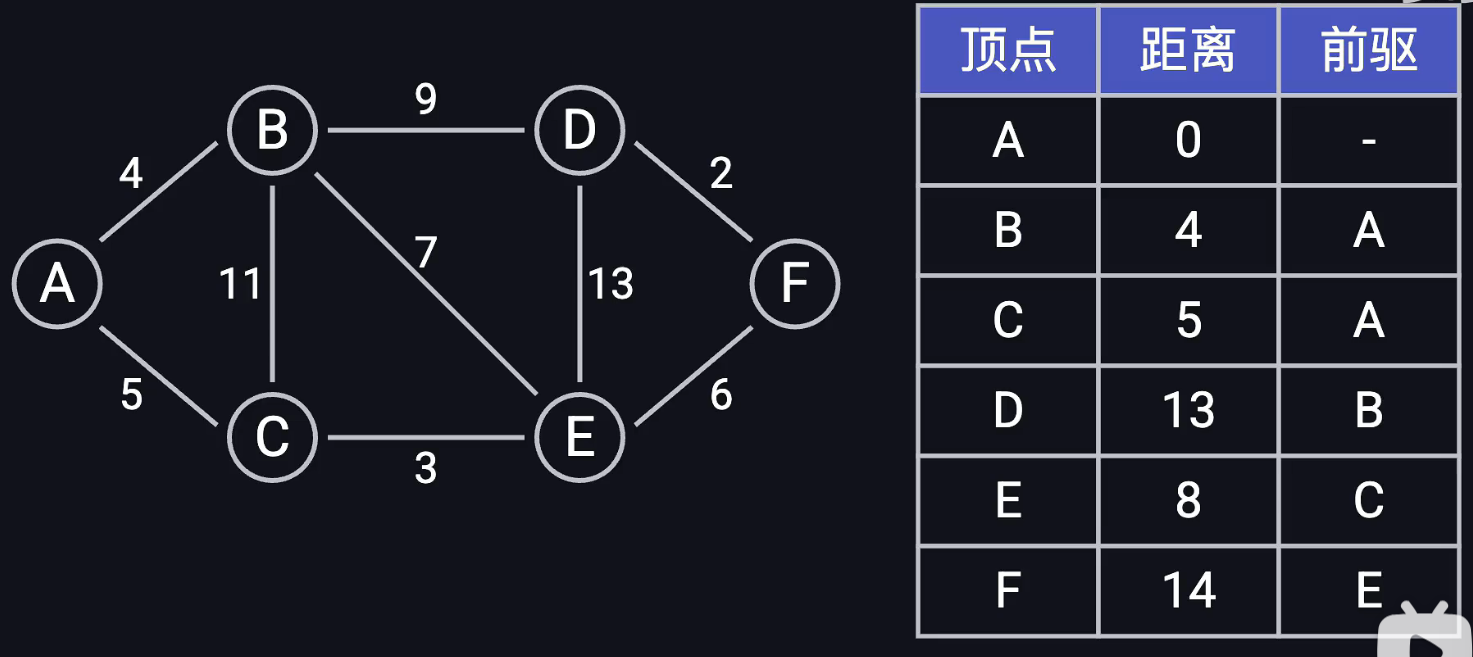
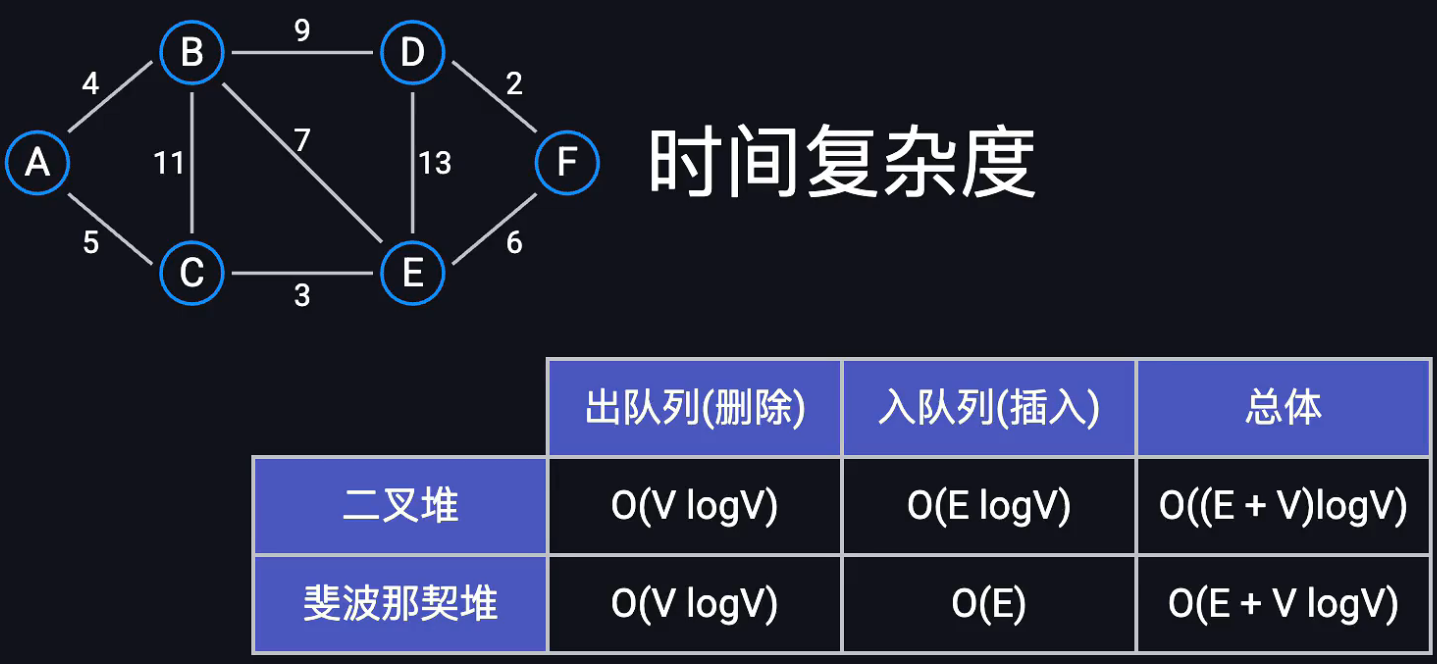
每次出队列(提取堆)要进行重拍,重拍开销logn,对于所有节点都要删除一次,因此nlogn;
每条边可能引发一次"松弛操作",从而导致一个顶点被重新插入堆中!
BellmanFord(不考)
依次遍历所有节点的所有边,即A->B A->C A->D,然后B->E C->B C->E。。。
重复V-1轮一定收敛,可能提前收敛
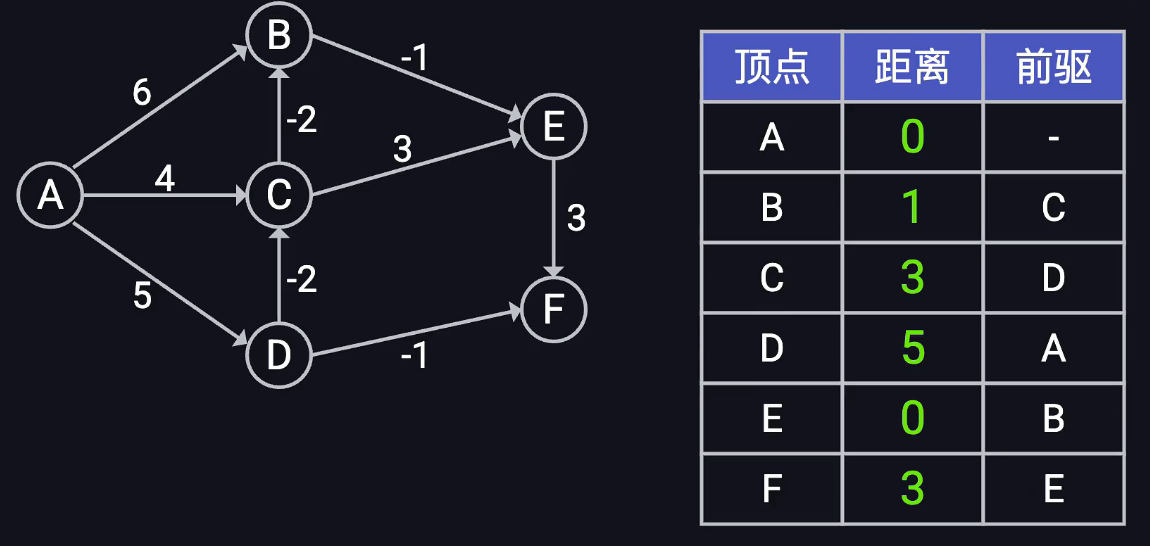
算法复杂度:O(V*E)
A*搜索算法
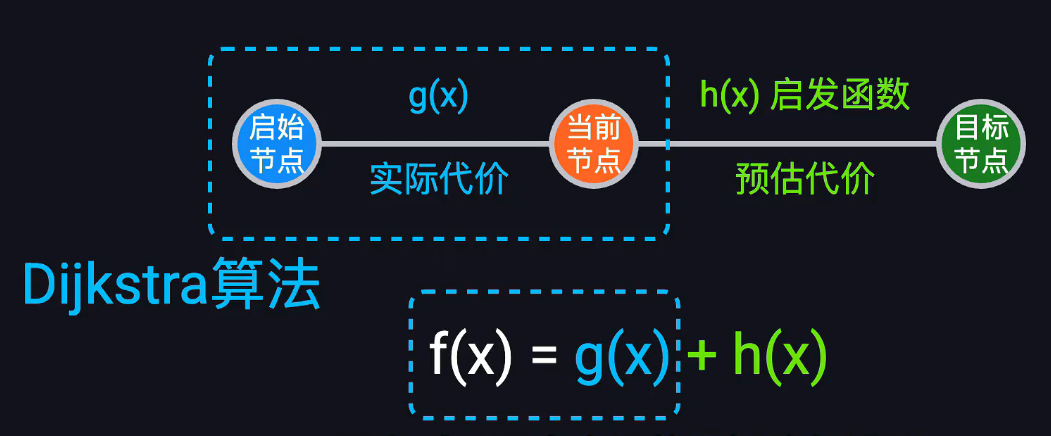
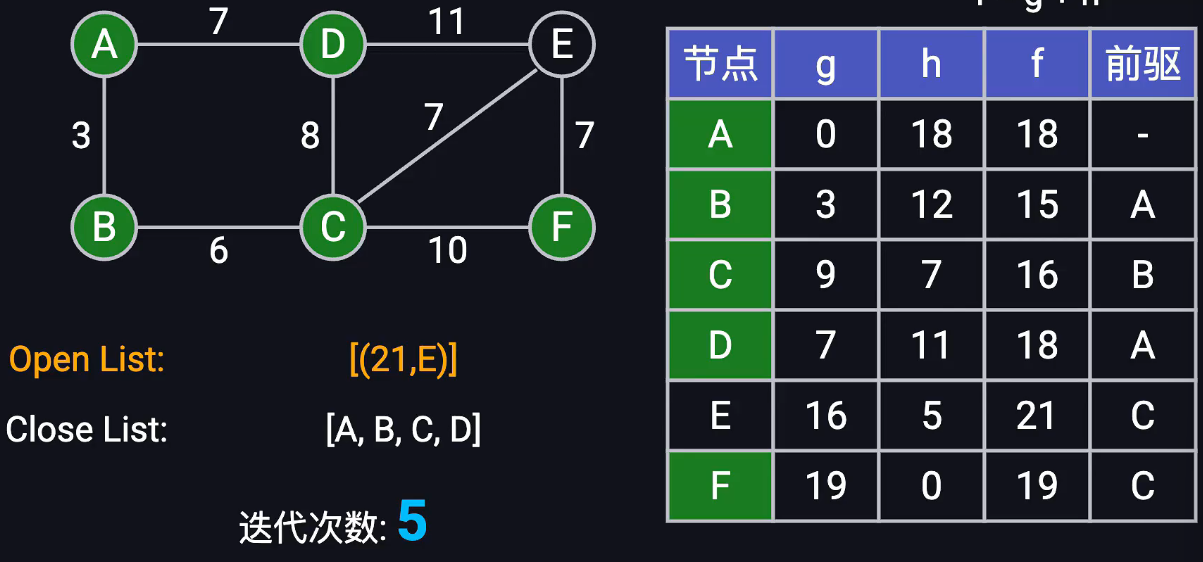
复杂度在O(E)~O(E+VlogV)之间
Floyd-Warshall 动态规划
D法是单源算法,如果要全源则需要n次
FW能一次性计算出所有点之间的最短路径
通过一张加权表和一张前驱表不断更新得到
distx是邻接矩阵,表达任意两点之间的最短距离
nextx是前驱表,记录下一跳
通过三层循环,选择kij,k是中继节点,i是起始,j是终点
不断更新k,相当于在任意两个节点之间插入另一个节点,看看有没有更短通路
更新n轮后一定会收敛
只要对角线为正,就证明没有负权环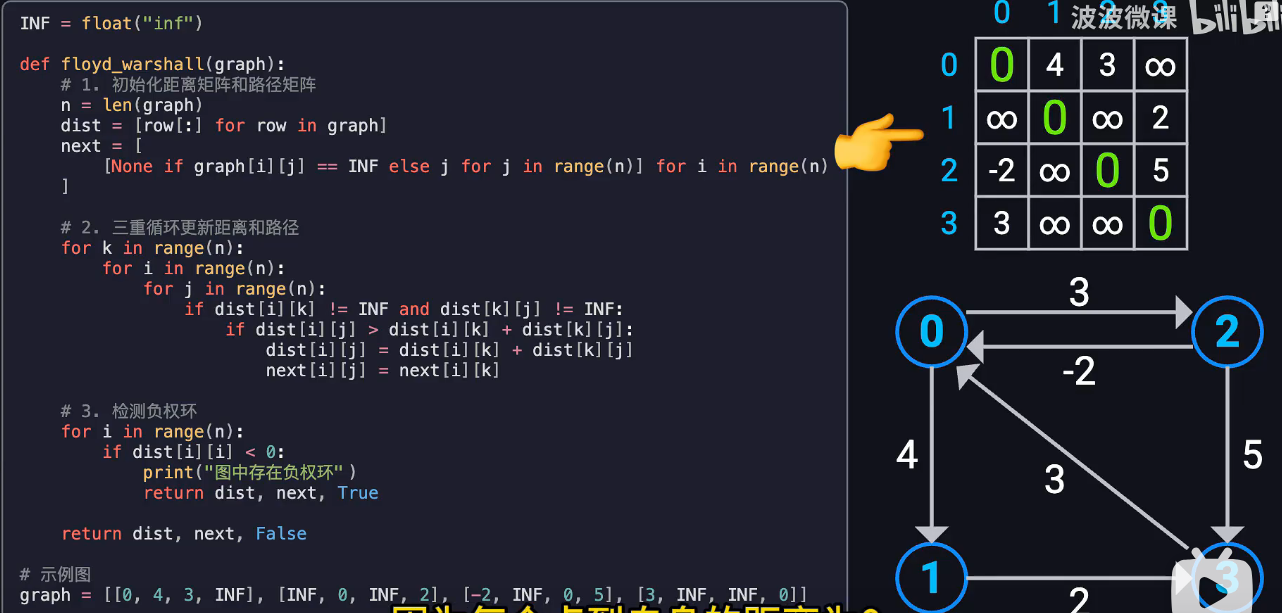
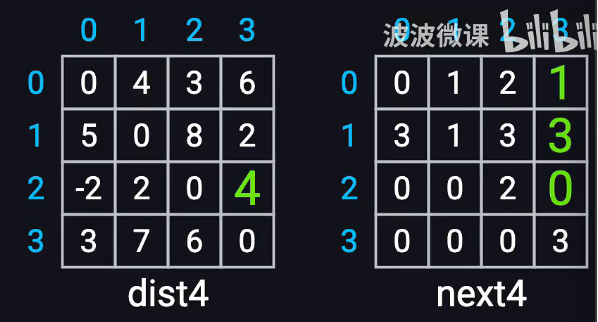
对于最终表,从2->3,先看next4,由0,为下一条,那么下一步就是0->3,是1,然后是1->3,找到最短路径2-0-1-3. 距离是dist4 2->3=4
算法复杂度:

第十六章
并查集
用于处理元素分组问题的数据结构,用于快速判断两个元素是否属于同1个集合,用于快速合并两个集合

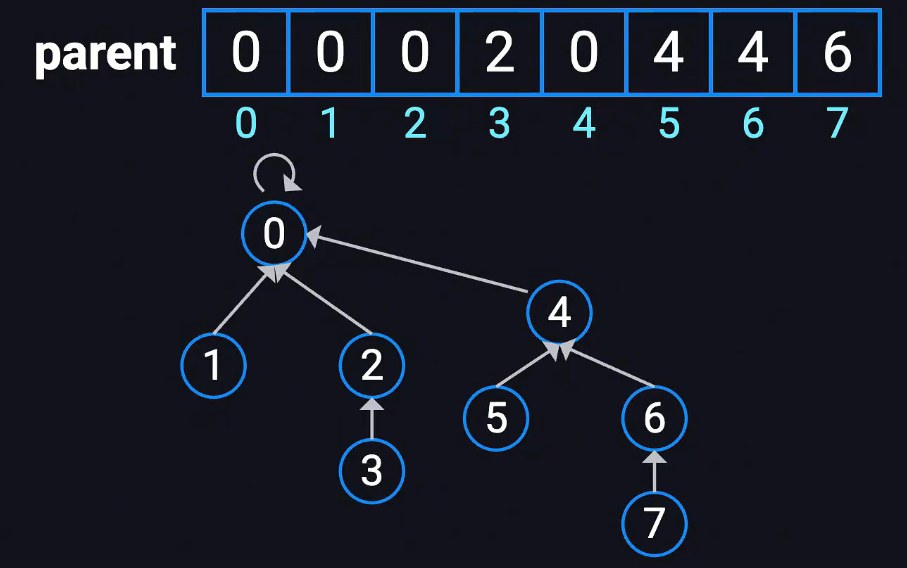
make_set()------每个元素独立为集合
union(x,y)------合并两个元素,使得第一个元素的牢大为第二个元素的牢大,把这两个涉及的集合合并为一个,直接修改数组
find(x)------找x的最终父节点是谁
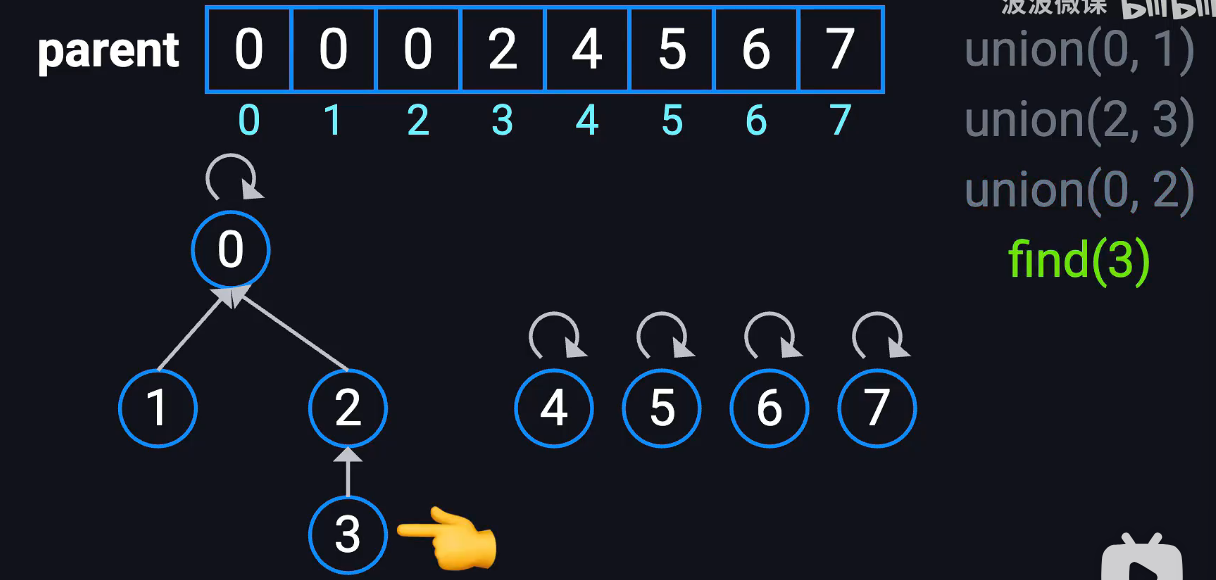
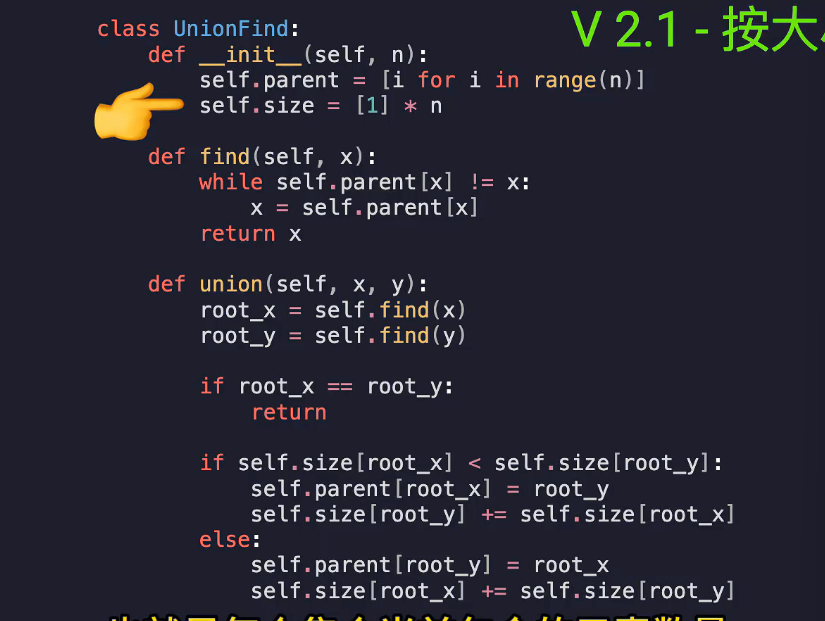
按秩合并
当树很深时,find效率会变低,因此使用两种方式,将节点多的挂载到节点少的 或将树高低的挂载在树高高的上
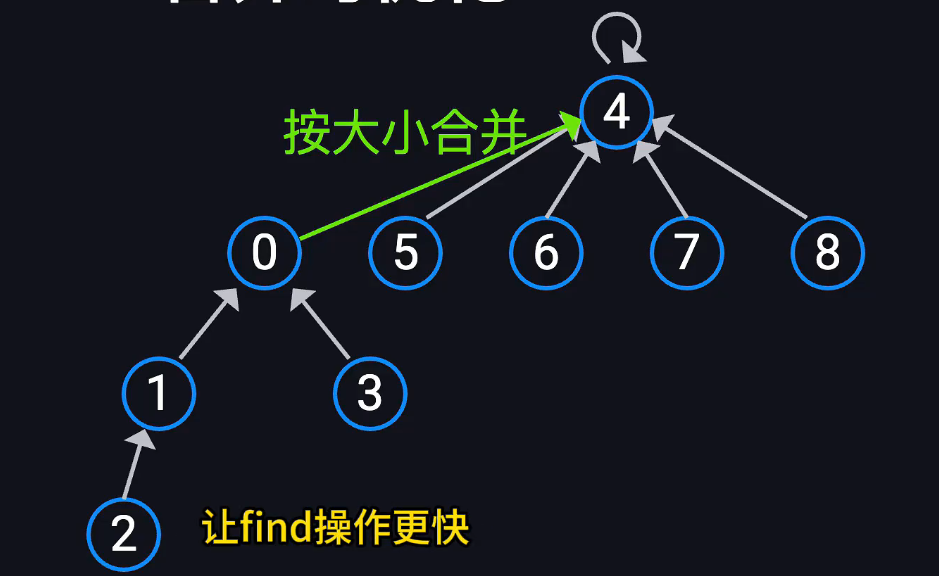
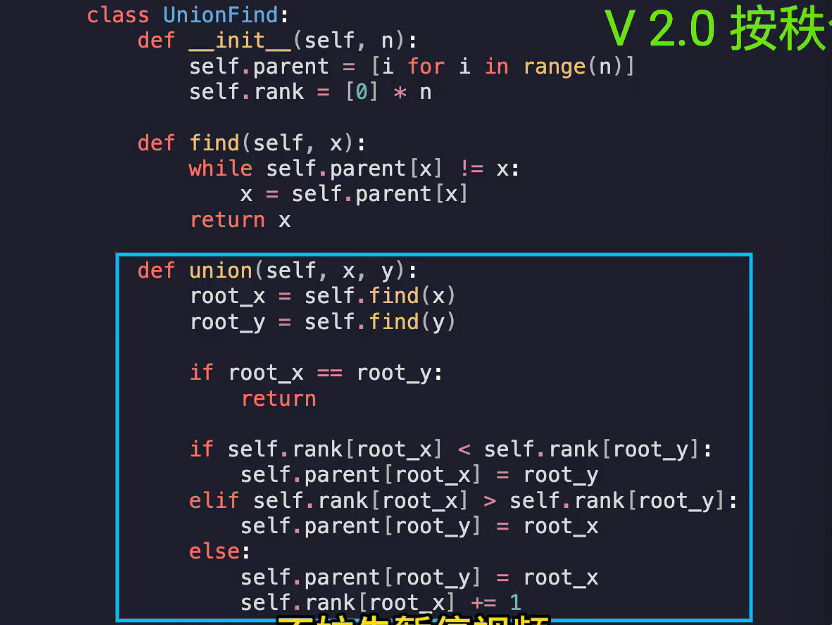
多加一个rank属性,初始化0
合并的时候先判断将rank矮的挂载到rank高的上
路径压缩------在查找的同时将路径上经过的节点全部挂载到根节点上

find的时候顺便将当前的根节点迭代挂载到根节点的根节点上,即将数组内的值更改为下一次找到的根节点的idx
时间复杂度O(4~5)
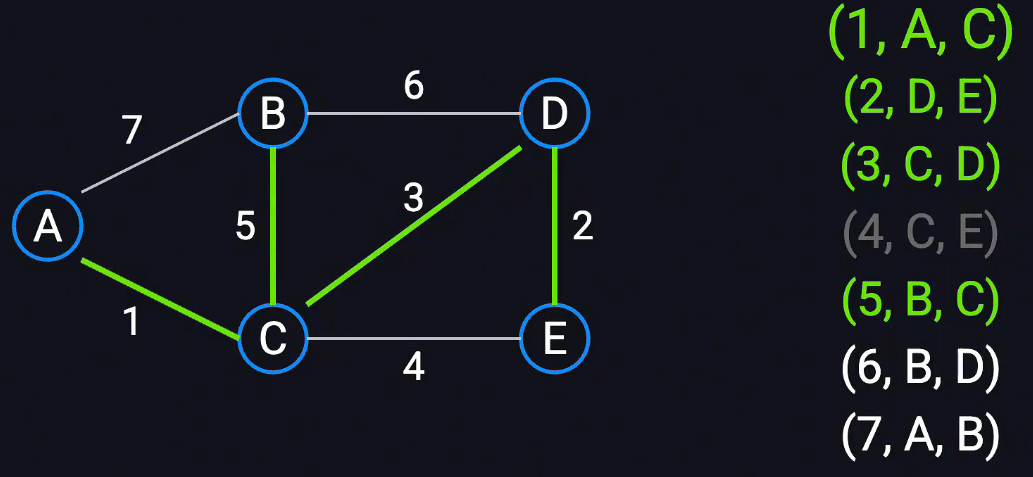
克鲁斯卡尔最小生成树ElogE
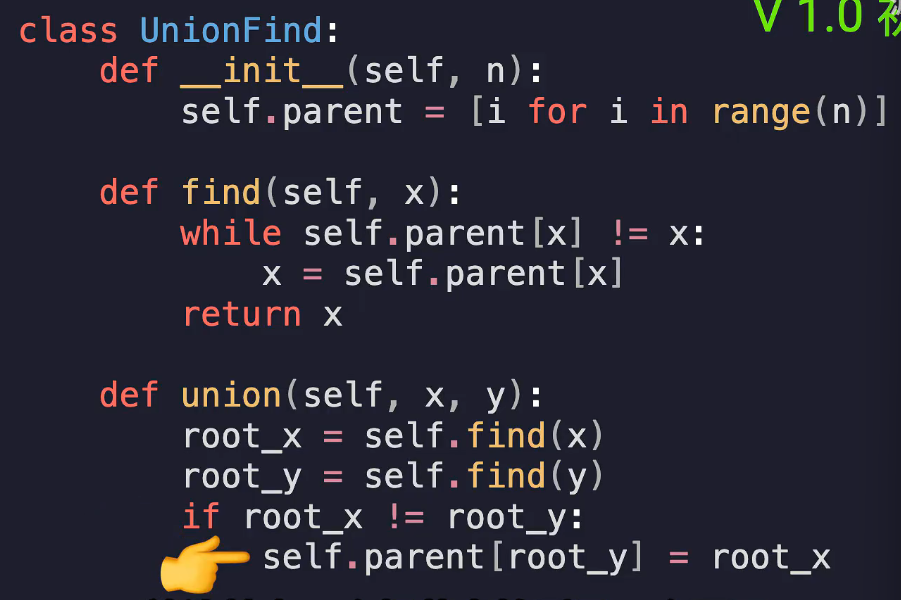
创建并查集类
包括find check两个函数,check通过find找到两个连通分支各自的代表元
如果一致则返回false,否则true
在主函数中,创建目标队列 与 uf对象
对每一条边遍历,根据权重排序,每次提取最小的边,
对其顶点进行判断,调用uf对象的check函数,如果返回true则证明为两个分支,可以选择,否则continue
直到n-1
这就设计了连通性判断,因此需要上面并查集的内容

这样的操作包括:
1.判断是否成环------是否联通 root_x=self.find(x) root_y=self.find(y) root_x == root_y?
2.将一条边加入生成树中------union()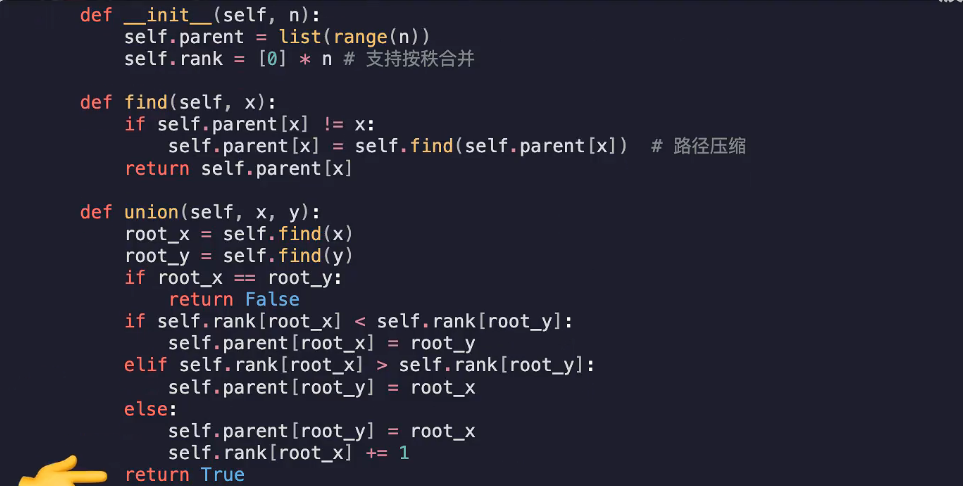
先创建UF集合,会自动拆为最小节点
然后堆边进行sort 复杂度logE,然后对于每条边进行判断:
如果uf.union能够执行,也就是UF输出True,不成环的情况下,就往mst中添加这条边,同时累加权重
直到mst的len=n-1

时间复杂度:

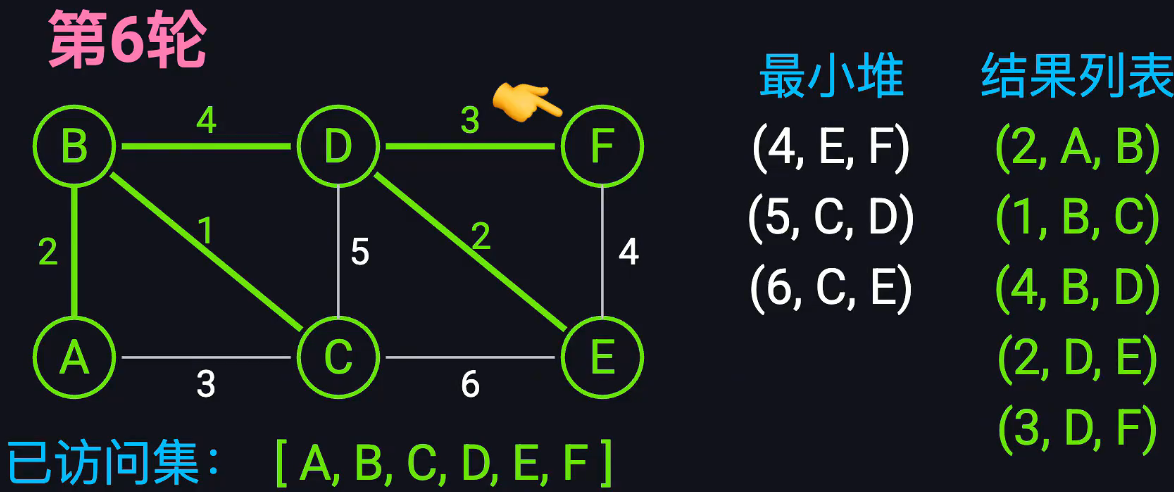
Prim最小生成树算法ElogV
创建邻接表、最小堆 目标队列 已访问 原始节点队列
创建结构体 包括起点 终点 权重
遍历所有边将其连接的点存入邻接表
初始时选择任意一个节点,探索其边,选择最小权重边,查看邻接表其终点是否在已访问列表中
如果没有则添加,并累计权重
同时将邻居节点的相邻边放入最小堆

开辟最小堆,维护当前可用探索的边,由于每次探索最小的,因此使用最小堆
开辟结果列表维护选取的边
开辟以访问集保存已经访问的顶点
开辟nodes集保存未访问的节点
 '
'

nodes用于存放当前可用访问的节点
visited存放已经访问的顶点
mst保存结果边
min_heap维护当前可选边
对于传入的每一条边,对于第一个顶点graph[u]添加权重为w,目的为v
对于第二个顶点graph[v]添加权重为w,目的为u
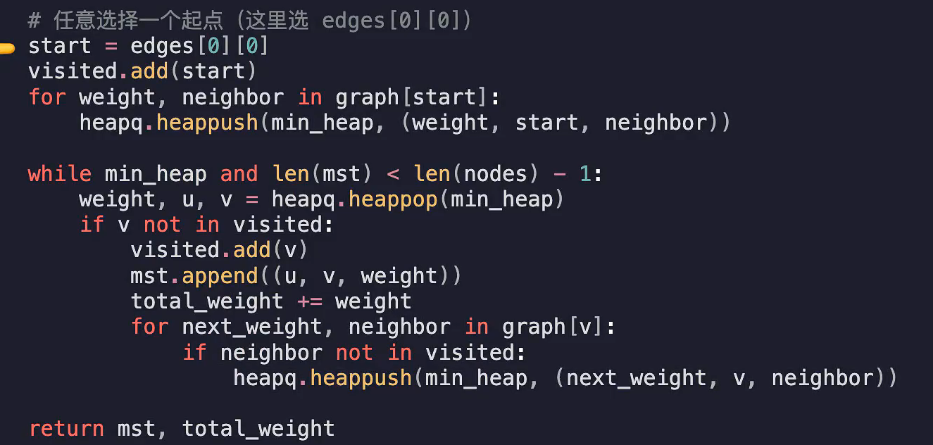
随机选一个起点。
将其放入已访问列表visited,然后把start顶点可连出去的所有边放入最小堆,堆会自动按权重从小到大排序
对于每一轮,取出堆中最小的边,如果其目标顶点没有访问过,就将其添加到visied中,然后将这条边放进mst目标列表中,同时累加权重
对于这条新加入顶点考虑,对于新顶点的其他边连接的节点,如果没有访问过,就全部放入堆中
直到n-1条边都被访问了
时间复杂度:
对于堆的处理复杂度都是logV 每条边最多被加入堆一次,因此堆操作数不超过E次,因此复杂度是O(ElogV)
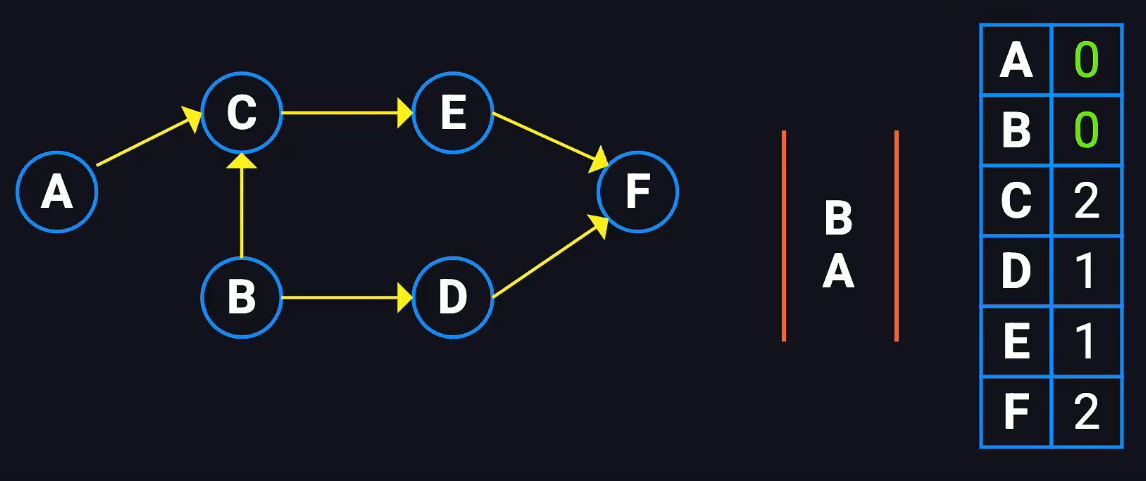
Kahn拓扑排序算法(入度为零即取出队列) V+E
入度 零度 原始 临界 目标 管理访问的队列
添加邻接表 对于每一条边存储始终点,并为终点在入度数组中加一
初始将0度节点加入目标队列,搜索其邻接节点,将其度减一
如果为0则加入零度队列
检查目标队列长度是否等于原始节点队列
解决依赖问题,找到合理的安装顺序
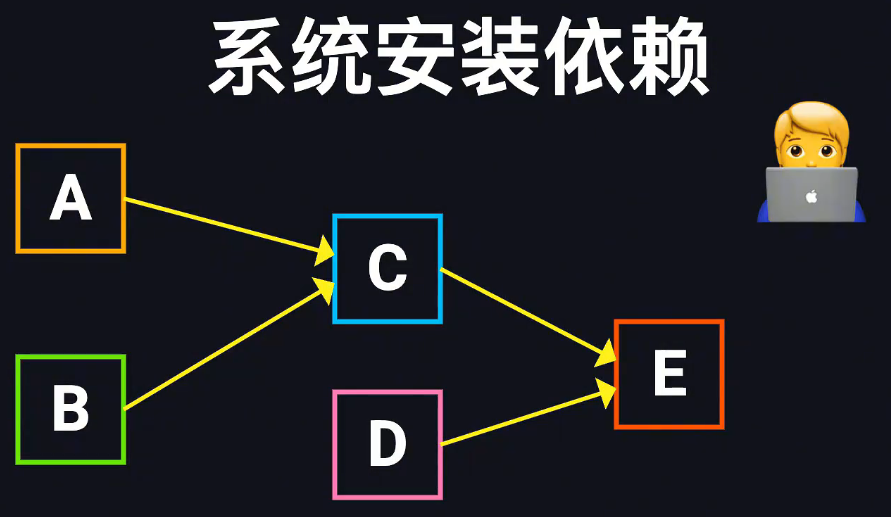
只要入度为零即可加入,加入后其指向的节点的入度减一
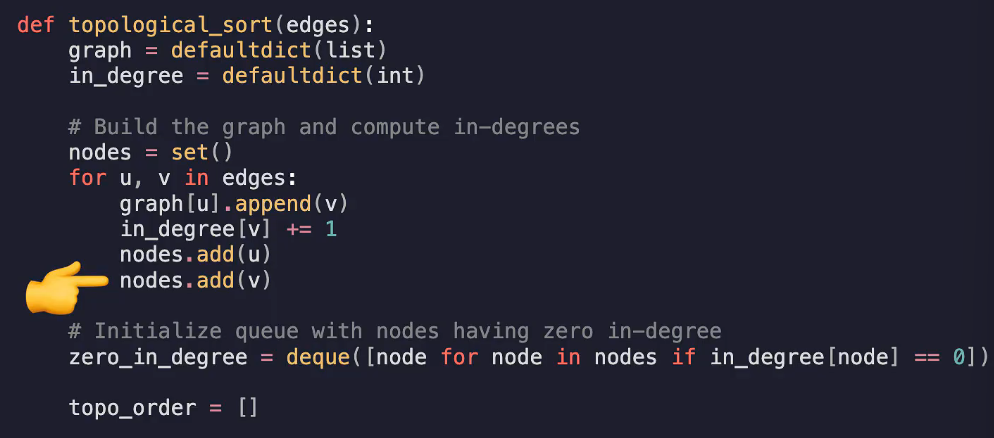
创建两个字典,一个字典用于记录每个节点的入度,一个用于构建邻接表(建图)
创建一个topo_order保存最终结果
遍历每条边,对于每对起点u终点v:将v加入u的邻接表,同时给v的入度加一
初始时将入度为0的节点全加入队列
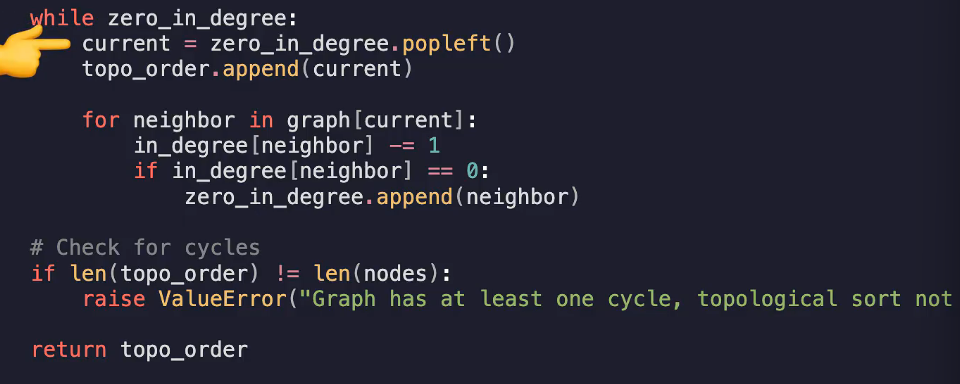
进入主循环后,每次从队列zero中取出一个节点current,将其放入最终结果topo_order中
访问器所有邻接点:for neighbor in graph
将邻接节点入度减一,如果邻接节点入度为0,则加入zero访问列表
最后检查len(topo_order)是否等于nodes的长度,如果不等于说明由环
时间复杂度:O(V+E)每个顶点和边添加一次
第十八章------分治
归并排序
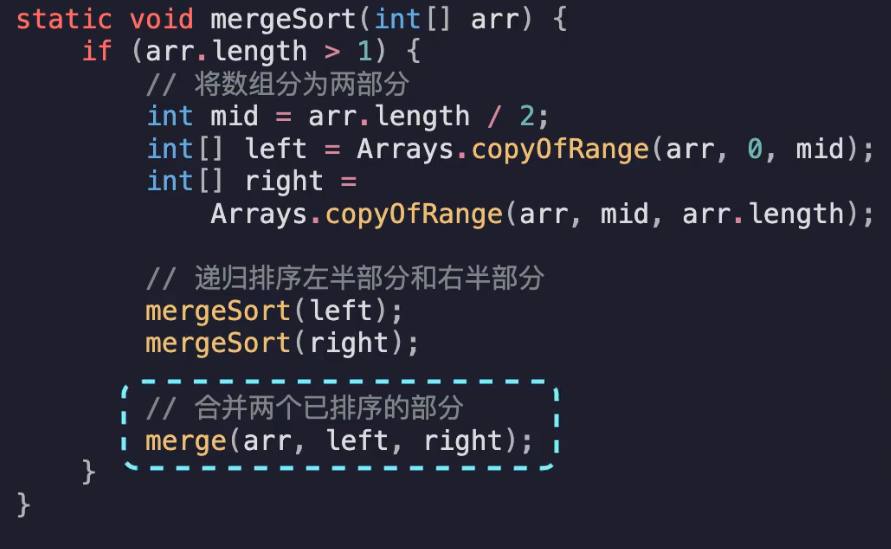

一路拆到一组只有一个元素,然后开始归并
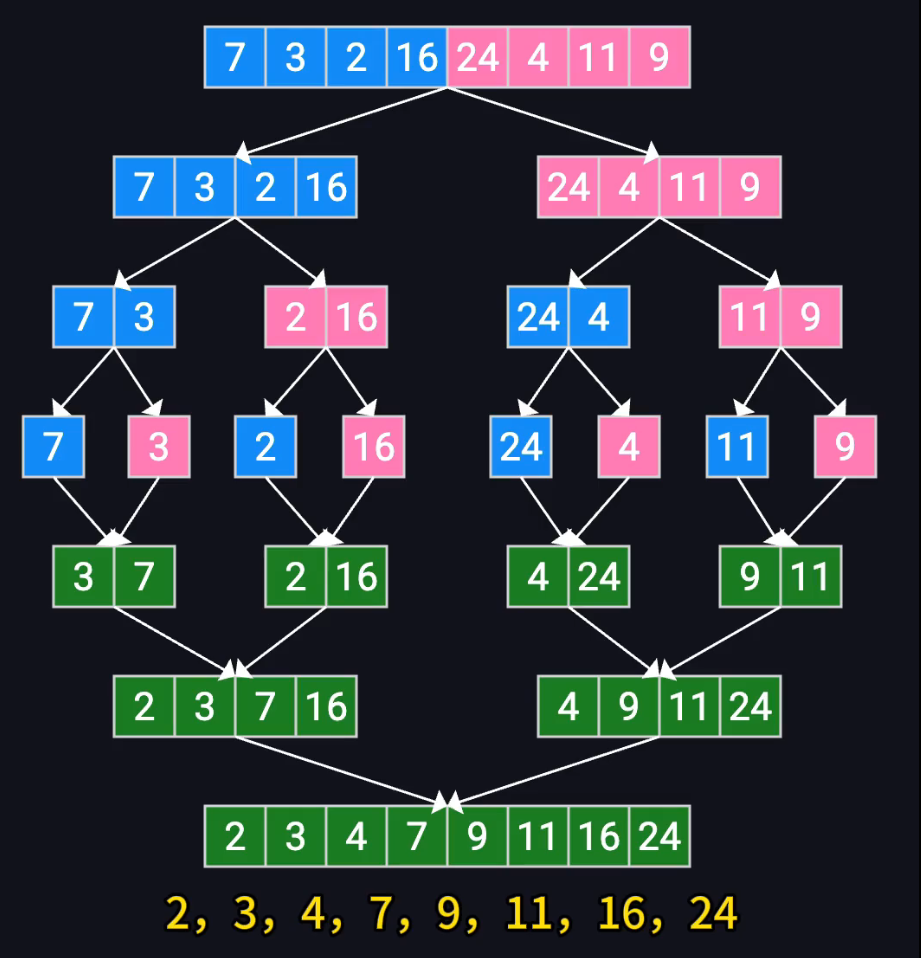
算法复杂度:
时间复杂度:O(nlogn) 递归深度是logn,然后每次合并需要n的复杂度
空间复杂度O(n)
快速排序
写一个快排和分区函数
快排首先调用分区函数进行分区
分区函数先设置基准值为最后一个,初始化指针指向low-1
对于low到high-1如果有比基准值大的放右侧,小的放左侧
接着递归调用快排,对分区的左右继续分区+快排
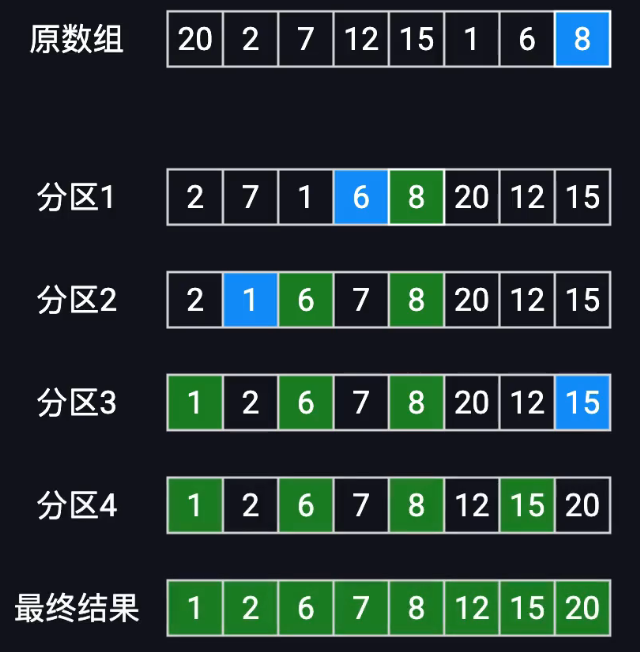
1.选择基准值
2.双指针分区(左边元素比基准值小 右边比基准值大)
3.递归排序 对左右分区执行选基准值并分区
j用于探索i用于标记,当j的值比基准值小则让i++然后交换ij的值,最后
i的值就是已经根据基准值分区的位置了,然后把基准值和i的位置交换,接着分治


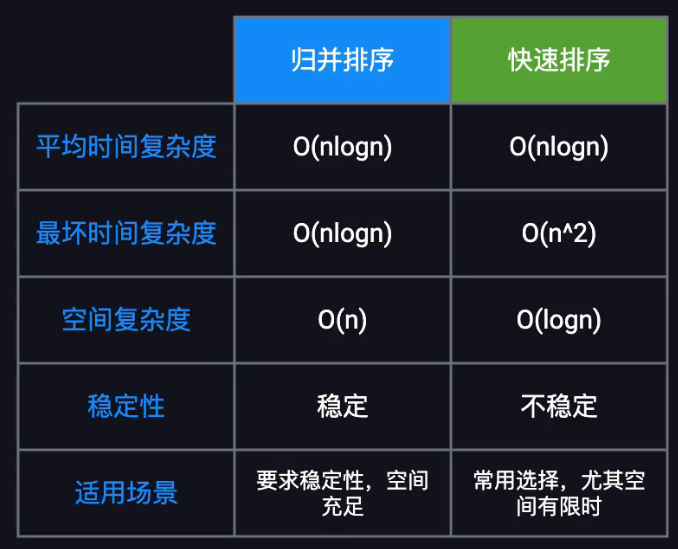
选择
算法设计的小技巧:
保护顺序的动态维护使用栈或队列,不保护顺序但要求按增减序排序的动态维护用最大最小堆
比如DFS BFS,DFS使用队栈 BFS 使用队列
克鲁斯卡尔和普利姆是使用最小堆
树结构用于急需要快速查找且需要保持数据的顺序
并查集会破坏前中后序 因此不能平替树