
文章目录
课题介绍
在低功耗物联网与边缘智能快速发展的背景下,定位系统正面临"高精度---低功耗---低成本"之间的长期矛盾。传统高精度定位方法通常依赖高采样率、高带宽或多传感器冗余设计,导致系统功耗和硬件复杂度显著上升,难以直接部署在大规模、长时工作的终端节点中。本课题从信号与信息处理角度出发,引入超分辨率(Super-Resolution, SR)技术,在不增加硬件资源或仅使用低分辨率、低采样率观测的条件下,实现定位精度的显著提升,为低功耗定位系统提供新的技术路径。
低功耗阵列信号模型(角度观测)
考虑一个低功耗均匀线阵 U L A ULA ULA,阵元数较少、快拍数受限。单目标窄带模型为
x ( t ) = a ( θ ) , s ( t ) + n ( t ) \mathbf{x}(t) = \mathbf{a}(\theta), s(t) + \mathbf{n}(t) x(t)=a(θ),s(t)+n(t)
其中
a ( θ ) = [ 1 e − j 2 π d λ sin θ ⋯ e − j 2 π ( M − 1 ) d λ sin θ ] ! T \mathbf{a}(\theta)= \begin{bmatrix} 1 & e^{-j2\pi \frac{d}{\lambda}\sin\theta} & \cdots & e^{-j2\pi \frac{(M-1)d}{\lambda}\sin\theta} \end{bmatrix}^{!T} a(θ)=[1e−j2πλdsinθ⋯e−j2πλ(M−1)dsinθ]!T
低功耗约束体现在:
- 阵元数 (M) 小
- 快拍数 (N) 小
- 信噪比偏低
协方差矩阵与子空间分解
R x = E [ x x H ] = A R s A H + σ 2 I \mathbf{R}_x = \mathbb{E}[\mathbf{x}\mathbf{x}^H] = \mathbf{A}\mathbf{R}_s\mathbf{A}^H + \sigma^2\mathbf{I} Rx=E[xxH]=ARsAH+σ2I
特征分解:
\\mathbf{R}_x = \\mathbf{U}_s\\boldsymbol{\\Lambda}_s\\mathbf{U}_s\^H * \\mathbf{U}_n\\boldsymbol{\\Lambda}_n\\mathbf{U}_n\^H
超分辨率角度估计(MUSIC)
P MUSIC ( θ ) = 1 a H ( θ ) U n U n H a ( θ ) P_{\text{MUSIC}}(\theta) = \frac{1}{\mathbf{a}^H(\theta)\mathbf{U}_n\mathbf{U}_n^H\mathbf{a}(\theta)} PMUSIC(θ)=aH(θ)UnUnHa(θ)1
由角度测量到定位
已知基站位置 p i = ( x i , y i ) \mathbf{p}_i=(x_i,y_i) pi=(xi,yi),测得 AOA 为 θ i \theta_i θi,目标位置 p = ( x , y ) \mathbf{p}=(x,y) p=(x,y)满足
tan θ i = y − y i x − x i \tan\theta_i = \frac{y-y_i}{x-x_i} tanθi=x−xiy−yi
最小二乘定位:
p ^ = arg min p ∑ i ( tan θ i ( x − x i ) − ( y − y i ) ) 2 \hat{\mathbf{p}} = \arg\min_{\mathbf{p}} \sum_i \left( \tan\theta_i(x-x_i)-(y-y_i) \right)^2 p^=argpmini∑(tanθi(x−xi)−(y−yi))2
MATLAB例程
功能:
- 少阵元、少快拍(低功耗)
- 对比:常规波束形成 vs MUSIC 超分辨率
- 输出清晰角度谱图
运行截图:
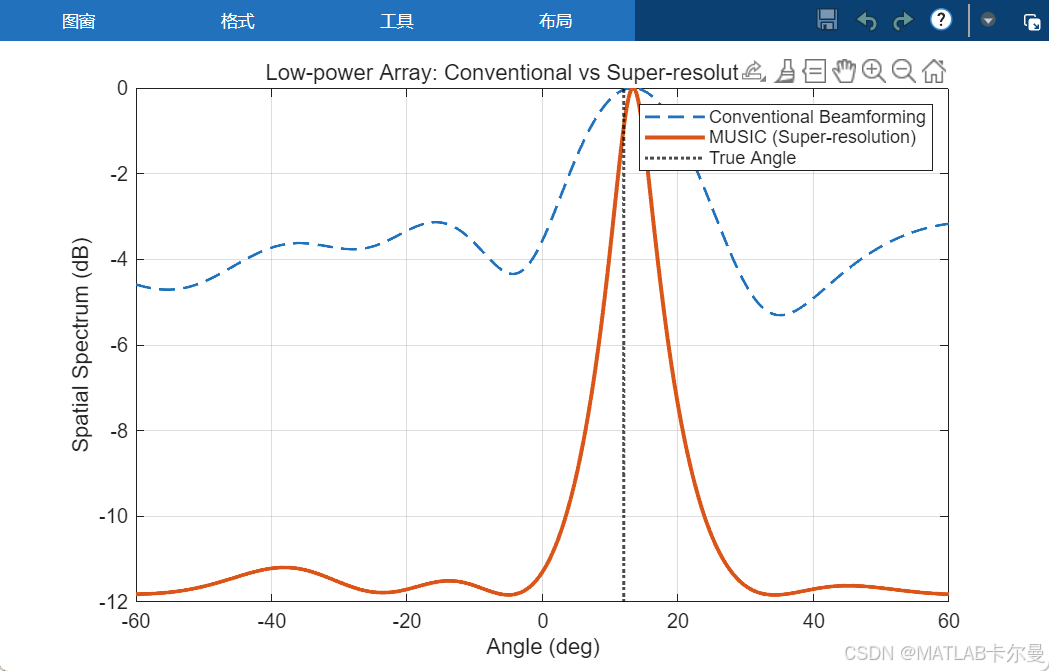
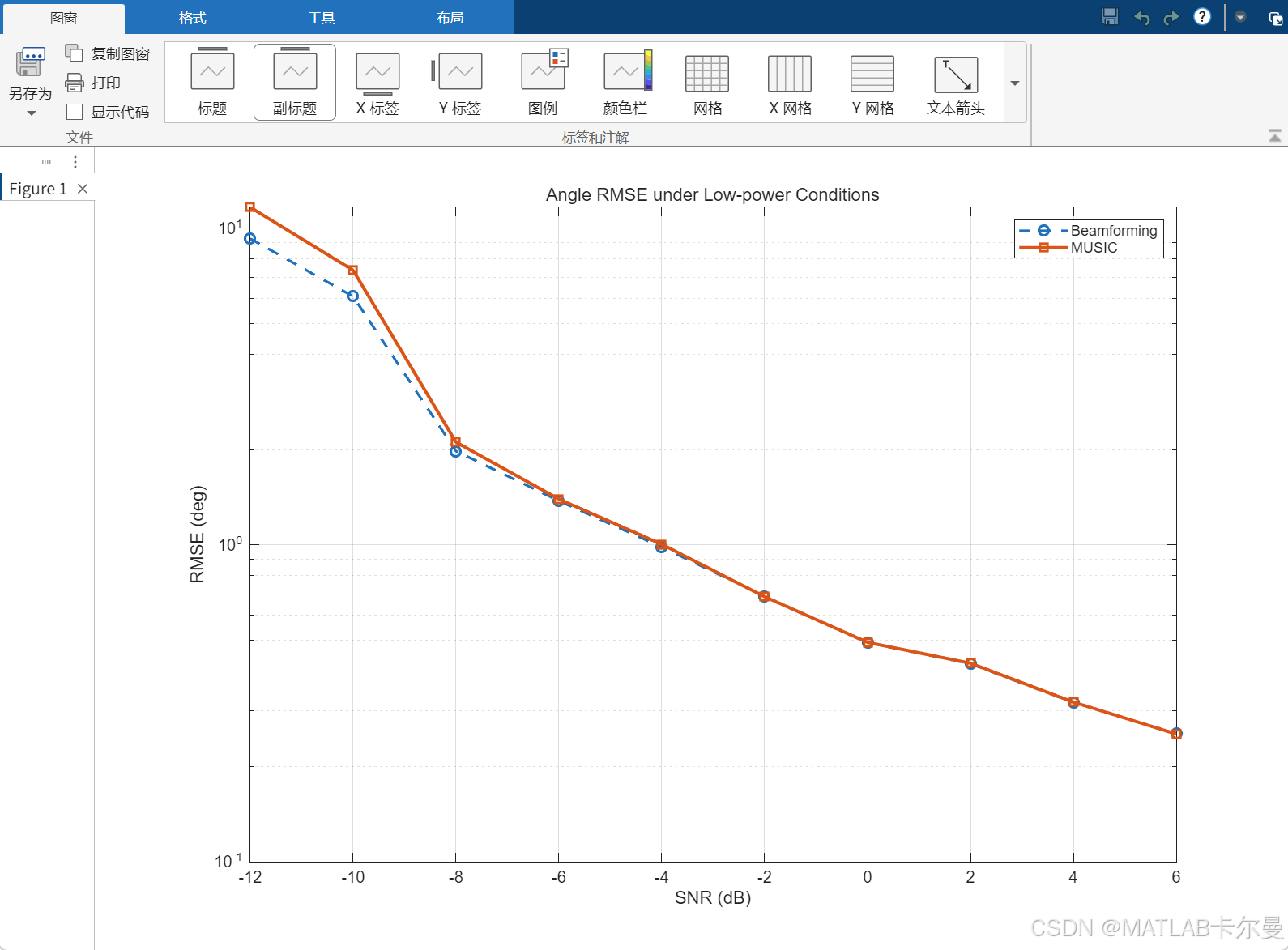
结果说明
在阵元数仅为 6、快拍数为 40、信噪比为−5dB的低功耗条件下,传统波束形成方法的主瓣宽度较大,角度分辨率明显受限;而基于子空间分解的 MUSIC 超分辨率算法仍能形成尖锐谱峰,准确指示目标方向。这表明,通过引入超分辨率信号处理方法,可以在不增加硬件复杂度与采样功耗的前提下,显著提升定位系统的角度观测精度,为低功耗定位系统提供了一条可行且有效的技术路径。
修改方向
- MUSIC → 稀疏贝叶斯超分辨率 AOA
- 超分辨率角度 → EKF/UKF 中的高精度观测更新
- 单站 AOA → 多站协同低功耗定位
- 角度 SR → TOA / TDOA / 多径抑制 SR
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者