【深度学习Day4】告别暴力拉平！MATLAB老鸟带你拆解CNN核心：卷积与池化 (附高频面试考点)

摘要：刚用 MLP 啃下了 MNIST，但那种把精美的 <math xmlns="http://www.w3.org/1998/Math/MathML"> 28 × 28 28 \times 28 </math>28×28 图片暴力 Flatten 成一条线的操作，总让我觉得像是在"暴殄天物"------像素原本的空间邻域信息全丢了！今天，作为一名 MATLAB 老鸟，我要用大家熟悉的图像处理视角，拆解 PyTorch 的核武器------torch.nn.Conv2d（卷积层）与 torch.nn.MaxPool2d（池化层）。本文不整虚的，从 MATLAB 卷积操作类比到 PyTorch 实战，既有参数详解、原理可视化逻辑，还有面试必背的维度计算公式，甚至加了卷积核可视化、特征图查看的硬核实操；搞懂这些，下一篇 CIFAR-10 实战才能真正"知其然也知其所以然"！

关键词：PyTorch, CNN, 卷积, 池化, 特征提取, 感受野, 维度计算, 面试题

1. 为什么要抛弃 MLP？(From Flatten to Feature)

在上一篇（Day3）中，我们用全连接网络（MLP）训练了 MNIST，准确率勉强到 97%+，但只要稍微把图片放大一点，MLP 就会立刻"露怯"------核心问题就两个，咱们用 MATLAB 老鸟能懂的"数字"说话：

1.1 空间结构丢失：从"看图"变成"看一串数字"

MLP 第一步就是 x.view(-1, 784)，把 28×28 的图片拉成 784 维的一维向量。这就像把一张拼图拆成碎片后打乱，只看碎片的颜色，却不管碎片的位置：

在 MLP 眼里，像素点 (0,0)（左上角）和 (0,1)（右邻像素）只是长向量里的第 0 个和第 1 个数，它完全不知道这两个点在原图上是"紧挨着的邻居"；
而人眼看图是"局部感知"：先看到数字 "8" 的上半圈，再看到下半圈，最后组合成 "8" 的形状------这正是 CNN 的核心逻辑：局部连接。

1.2 参数量爆炸：MLP 根本扛不住大图片

咱们算一笔账：

MNIST 是 28×28 灰度图，MLP 输入层 784 个节点，若隐藏层 512 个节点，第一层权重参数 = 784×512 = 401,408 个；
换成 224×224 的 RGB 彩图（比如手机拍的照片），MLP 输入层 = 224×224×3 = 150,528 个 节点，若隐藏层 1000 个节点，第一层权重 = 150,528×1000 = 1.5 亿个参数！

别说训练了，光把这些参数存到内存里，普通显卡都扛不住。

1.3 CNN 的破局思路：局部连接 + 权值共享

CNN 解决这两个问题靠的是 "两大法宝" ：

局部连接：每个卷积核只看图片的一小块（比如 3×3），而非全图，参数量直接砍半；
权值共享：同一个卷积核扫遍整张图（比如用 "边缘检测核" 扫全图找边缘），而非每个像素都配一套权重，参数量再砍 N 倍。

用 MATLAB 类比：这就像你用 Sobel 算子（一个 3×3 的卷积核）处理整张图片时，不会给图片每个位置都做一个专属 Sobel 核，而是用同一个核扫完全图------CNN 只是把 "固定的 Sobel 核" 换成了 "能自己学的核" 而已。

2. 核心武器一：卷积层 (Convolution)

卷积层是 CNN 的 "特征提取器"，也是面试问得最多的模块。咱们从 MATLAB 老鸟熟悉的视角，一步步拆透它。附上Convolution | NVIDIA Developer直观的图：

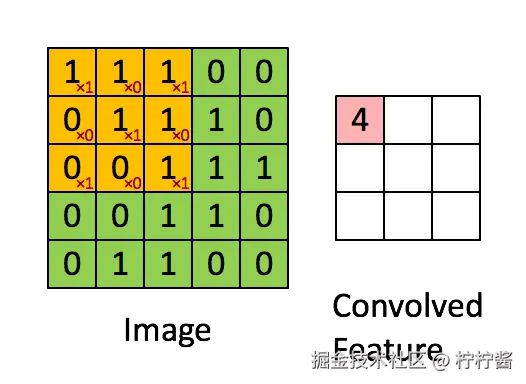
2.1 MATLAB 视角的 "卷积" vs 深度学习的 "卷积"

先回顾 MATLAB 里的图像卷积操作------这是咱们的 "舒适区"，从这里切入，CNN 卷积就一点都不抽象了：

matlab 复制代码

% MATLAB 经典操作：用 Sobel 算子做边缘检测
img = imread('mnist_sample.png'); % 读入 28×28 灰度图
img_gray = rgb2gray(img); % 转灰度
H = fspecial('sobel'); % 定义 Sobel 卷积核（3×3，固定值）
result = imfilter(img_gray, H); % 用固定核 "卷" 图片
imshow(result); % 看到边缘特征

MATLAB 里的卷积：卷积核是人工定义的（比如 Sobel、高斯、拉普拉斯），目的是提取预设的特征（边缘、模糊、锐化） 。

而 PyTorch 里的 nn.Conv2d：卷积核是随机初始化的，然后通过反向传播"学"出来的------网络自己决定该学一个 "边缘检测核"，还是 "拐角检测核"，甚至 "数字笔画检测核"。

举个直观的例子：

普通卷积：你告诉电脑 "用 Sobel 找边缘"；
CNN 卷积：电脑自己试错，最后发现 "用这个核找边缘，模型准确率最高"，于是把这个核的参数记下来。

这就是 CNN "特征提取"的本质：把人工设计特征（MATLAB 卷积）换成了自动学习特征（PyTorch 卷积） 。

2.2 PyTorch 中 nn.Conv2d 参数大拆解（面试必考）

nn.Conv2d 的参数是新手最容易晕的地方，咱们逐个击破，每个参数都配"MATLAB 类比 + 实战效果"：

python 复制代码

import torch.nn as nn
# 核心定义：Conv2d 基础用法
conv_layer = nn.Conv2d(
    in_channels=3,      # 输入通道数
    out_channels=16,    # 输出通道数（卷积核数量）
    kernel_size=3,      # 卷积核大小
    stride=1,           # 步长
    padding=1,          # 填充
    dilation=1,         # 膨胀率（新手先忽略，面试偶尔问）
    groups=1,           # 分组卷积（新手先忽略）
    bias=True           # 是否加偏置（默认True）
)

① in_channels & out_channels：通道数的 "厚度魔法"

这是 CNN 最抽象的概念，用 "图片厚度" 类比：

in_channels（输入通道数） ：输入图片有多 "厚" ？
- 灰度图（MNIST）：厚度=1 → in_channels=1；
- RGB 彩图（CIFAR-10）：厚度=3（红、绿、蓝各一层）→ in_channels=3；
- 卷积层输出的特征图：比如上一层输出 16 通道 → 这一层 in_channels=16。

✅ MATLAB 类比：就像 MATLAB 里处理多通道图像（cat(3, R, G, B)），每个通道是独立的图层。

out_channels（输出通道数） ：你想用多少个"不同的滤镜"观察图片？
- 设置 out_channels=16 → 网络会同时训练 16 个不同的卷积核；
- 每个卷积核扫一遍输入图片，输出一张 "特征图"；
- 最终输出 = 16 张特征图叠在一起（厚度 = 16）。

✅ 直观理解：16 个卷积核就像 16 个不同的 "滤镜" ------ 有的滤镜找边缘，有的找拐角，有的找纹理，最后把 16 张滤镜效果叠起来，就是 CNN 提取的 "特征"。

② kernel_size：卷积核的"视野大小"

卷积核是 CNN 看图片的"小窗口"，常见值和选择逻辑：

kernel_size=3：业界首选（VGGNet 证明：堆叠 2 个 3×3 卷积 ≈ 1 个 5×5 卷积，但参数量更少）；

✅ 参数量对比：3×3 核 = 9 个参数，5×5 核 = 25 个参数，差距一目了然；

kernel_size=5：偶尔用在第一层（需要更大的初始视野）；
kernel_size=1：面试高频考点！看似"没用"，实则是"降维神器"（下文面试题详细说）。

③ stride：卷积核的"滑动步子"

卷积核在图片上滑动的步长，直接影响输出特征图的尺寸：

stride=1：步步为营，每个像素都扫（默认值，保留更多细节）；
stride=2：隔一个像素扫一次，输出尺寸直接减半（轻量级下采样）；

✅ MATLAB 类比：就像 imresize(img, 0.5) 缩小图片，但 stride=2 是"带特征提取的缩小"，而非单纯缩放。

④ padding：防止图片 "越卷越小" 的关键

卷积核扫到图片边缘时，会因为 "没地方落脚" 导致输出尺寸变小 ------ padding 就是在图片周围补 0，解决这个问题：

padding=0（Valid Padding）：不补 0，输出尺寸必然变小（比如 32×32 图片用 3×3 核，输出 30×30）；
padding=1（Same Padding）：补 1 圈 0，32×32 图片用 3×3 核，输出还是 32×32（尺寸不变）；

✅ 记忆技巧：padding = (kernel_size - 1) // 2 → 3×3 核 padding=1，5×5 核 padding=2，刚好实现 Same Padding。

2.3 硬核补充：卷积层的权值共享计算

为什么 CNN 参数量少？核心是 "权值共享" ------ 咱们算一笔账：

假设输入是 32×32×3 彩图，卷积层 out_channels=16，kernel_size=3；
每个卷积核的参数 = 3×3×3 = 27 个（3 通道 × 3×3 核）；
16 个卷积核总参数 = 16×27 = 432 个；
对比 MLP：输入 32×32×3=3072 节点，隐藏层 16 节点，参数=3072×16=49,152 个；

→ CNN 参数量只有 MLP 的 1/114！这就是权值共享的威力。

3. 核心武器二：池化层 (Pooling)

卷积层提取的特征图还是太大（比如 32×32×16），包含大量冗余信息（比如背景、重复纹理）------ 池化层就是 "特征浓缩器"，核心作用是 "降维不减效"。

3.1 最常用的 MaxPool2d：只留 "最显眼的特征"

nn.MaxPool2d 逻辑简单到离谱，但效果极佳：在指定窗口（比如 2×2）里，只保留最大值，其余值全部扔掉。

python 复制代码

# 2×2 最大池化，步长 2（尺寸减半）
pool_layer = nn.MaxPool2d(kernel_size=2, stride=2)

为什么选"最大值"？

最大值代表窗口内 "最显著的特征" ------ 比如 2×2 窗口里有一个像素值是 255（亮边），其余是 0，保留 255 就等于保留了 "边缘" 这个核心特征，扔掉 0 不影响结果。

最大池化的两大核心作用（面试必答）：

降维提速：2×2 池化 + stride=2 → 特征图长宽减半，数据量减少 75%，训练速度直接翻倍；
平移不变性：物体稍微移动（比如数字 "8" 偏了 1 个像素），最大值还在窗口里，输出不变，模型鲁棒性大幅提升。

✅ MATLAB 类比：就像 blockproc(img, [2 2], @(x) max(x.data(:)))，对每个 2×2 块取最大值，本质是 "带特征筛选的下采样"。

3.2 补充：AvgPool2d（平均池化）什么时候用？

除了最大池化，还有平均池化（取窗口内平均值），两者的选择逻辑：

MaxPool2d：适合提取 "边缘、纹理" 等局部显著特征（分类任务首选）；
AvgPool2d：适合保留 "全局亮度、背景" 等整体信息（分割/检测任务偶尔用）；

❌ 避坑：别在分类任务的关键层用 AvgPool2d，会丢失核心特征，导致准确率下降。

3.3 池化层的 "坑"：过度池化

堆叠太多池化层，导致特征图太小（比如 32×32 → 16×16 → 8×8 → 4×4），最后特征丢失严重。

✅ 实战原则：分类任务中，池化层最多用 2~3 层（比如 CIFAR-10 用 2 层池化，从 32×32 到 8×8 就够了）。

4. 硬核实战：手算维度（面试必考！）

算法岗笔试/面试中，"计算卷积/池化后的维度" 是 100% 必考的题 ------ 别光会调包，必须会手动算！

4.1 通用维度计算公式

先记牢卷积层和池化层的通用公式（用 MATLAB 老鸟熟悉的 "向下取整" 逻辑）：

卷积层维度公式

输入尺寸： <math xmlns="http://www.w3.org/1998/Math/MathML"> H i n × W i n H_{in} \times W_{in} </math>Hin×Win

卷积参数：kernel_size=K, stride=S, padding=P

输出尺寸：

<math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ⌊ H i n + 2 × P − K S + 1 ⌋ , W o u t = ⌊ W i n + 2 × P − K S + 1 ⌋ H_{out} = \left\lfloor \frac{H_{in} + 2 \times P - K}{S} + 1 \right\rfloor, \quad W_{out} = \left\lfloor \frac{W_{in} + 2 \times P - K}{S} + 1 \right\rfloor </math>Hout=⌊SHin+2×P−K+1⌋,Wout=⌊SWin+2×P−K+1⌋

（ <math xmlns="http://www.w3.org/1998/Math/MathML"> ⌊ ⋅ ⌋ \lfloor \cdot \rfloor </math>⌊⋅⌋ 是向下取整，比如 (31-3)/2 +1 = 15 → 刚好整除）

池化层维度公式

池化层没有 padding（少数情况有，但面试不考），公式简化为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ⌊ H i n − K S + 1 ⌋ , W o u t = ⌊ W i n − K S + 1 ⌋ H_{out} = \left\lfloor \frac{H_{in} - K}{S} + 1 \right\rfloor, \quad W_{out} = \left\lfloor \frac{W_{in} - K}{S} + 1 \right\rfloor </math>Hout=⌊SHin−K+1⌋,Wout=⌊SWin−K+1⌋

4.2 多案例实操（从易到难）

咱们用 CIFAR-10（32×32 RGB 图）做例子，覆盖面试常见场景：

案例 1：Same Padding 卷积（尺寸不变）

输入： <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 3 32 \times 32 \times 3 </math>32×32×3

卷积层：nn.Conv2d(3, 16, 3, stride=1, padding=1)

计算：

<math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ( 32 + 2 × 1 − 3 ) / 1 + 1 = 32 H_{out} = (32 + 2×1 - 3)/1 + 1 = 32 </math>Hout=(32+2×1−3)/1+1=32

输出： <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 16 32 \times 32 \times 16 </math>32×32×16（尺寸不变，通道数从 3→16）

案例 2：Valid Padding 卷积（尺寸缩小）

输入： <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 3 32 \times 32 \times 3 </math>32×32×3

卷积层：nn.Conv2d(3, 16, 3, stride=1, padding=0)

计算：

<math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ( 32 + 0 − 3 ) / 1 + 1 = 30 H_{out} = (32 + 0 - 3)/1 + 1 = 30 </math>Hout=(32+0−3)/1+1=30

输出： <math xmlns="http://www.w3.org/1998/Math/MathML"> 30 × 30 × 16 30 \times 30 \times 16 </math>30×30×16（尺寸缩小 2 像素）

案例 3：卷积 + 池化（组合操作）

输入： <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 3 32 \times 32 \times 3 </math>32×32×3

步骤 1：卷积（3→16，3×3，padding=1，stride=1）→ <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 16 32×32×16 </math>32×32×16

步骤 2：池化（2×2，stride=2）→ <math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ( 32 − 2 ) / 2 + 1 = 16 H_{out}=(32-2)/2 +1=16 </math>Hout=(32−2)/2+1=16

最终输出： <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 × 16 × 16 16 \times 16 \times 16 </math>16×16×16（尺寸减半，通道数不变）

案例 4：stride=2 卷积（替代池化）

输入： <math xmlns="http://www.w3.org/1998/Math/MathML"> 32 × 32 × 3 32 \times 32 \times 3 </math>32×32×3

卷积层：nn.Conv2d(3, 16, 3, stride=2, padding=1)

计算：

<math xmlns="http://www.w3.org/1998/Math/MathML"> H o u t = ( 32 + 2 × 1 − 3 ) / 2 + 1 = 16 H_{out} = (32 + 2×1 -3)/2 +1 = 16 </math>Hout=(32+2×1−3)/2+1=16

输出： <math xmlns="http://www.w3.org/1998/Math/MathML"> 16 × 16 × 16 16×16×16 </math>16×16×16（一步实现"卷积+下采样"，面试常考这种替代方案）

4.3 验证技巧：用 PyTorch 跑一遍

写两行代码验证 ------ 这是 Debug 复杂网络的核心技巧：

python 复制代码

import torch
import torch.nn as nn

# 模拟 CIFAR-10 图片：Batch=1, Channel=3, Height=32, Width=32
dummy_img = torch.randn(1, 3, 32, 32)
print(f"原始尺寸: {dummy_img.shape}")  # torch.Size([1, 3, 32, 32])

# 案例 4 验证：stride=2 卷积
conv_stride2 = nn.Conv2d(3, 16, 3, stride=2, padding=1)
x = conv_stride2(dummy_img)
print(f"stride=2 卷积后尺寸: {x.shape}")  # [1, 16, 16, 16]

5. 硬核实操：CNN 积木块 + 特征可视化

光算维度不够，咱们搭一个完整的 CNN 基础块，还能看到 "卷积核长啥样" "特征图是什么效果"。

5.1 搭建 CNN 基础积木块（含激活函数）

CNN 不是孤立的卷积+池化，必须加激活函数（ReLU）引入非线性，否则多层卷积 = 单层卷积：

python 复制代码

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 定义一个 CNN 基础块（卷积 + ReLU + 池化）
class CNNBlock(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(CNNBlock, self).__init__()
        # 卷积+ReLU+池化 组合
        self.conv = nn.Conv2d(in_channels, out_channels, 3, stride=1, padding=1)
        self.relu = nn.ReLU()  
        self.pool = nn.MaxPool2d(2, stride=2)
    
    def forward(self, x):
        x = self.conv(x)
        x = self.relu(x)
        feat_map = x  # 保存卷积 + ReLU后的特征图
        x = self.pool(x)
        return x, feat_map

# 1. 导入图片（用我的 Kuromi 头像）
img = Image.open("Kuromi.jpg")
transform = transforms.ToTensor()
img_tensor = transform(img)
img_tensor = img_tensor.unsqueeze(0) # [1, 3, H, W]
# 2. 实例化 CNN 块
cnn_block = CNNBlock(3, 16)
# 3. 前向传播
output, feat_map = cnn_block(dummy_img)

5.2 可视化 1：看卷积核长啥样

训练前的卷积核是随机初始化的，咱们把它画出来（学之前的核）：

python 复制代码

# 提取卷积层的权重（卷积核）
conv_weights = cnn_block.conv.weight.data  # 形状：[16, 3, 3, 3]（16个核，3通道，3×3）

# 画前8个卷积核（每个核的3个通道）
fig, axes = plt.subplots(8, 3, figsize=(8, 16))
for i in range(8):
    # 取第i个卷积核的3个通道（R/G/B）
    for c in range(3):
        kernel = conv_weights[i, c, :, :].cpu().numpy()
        # 归一化到0~1（方便显示）
        kernel = (kernel - kernel.min()) / (kernel.max() - kernel.min())
        axes[i, c].imshow(kernel, cmap='gray')
        axes[i, c].axis('off')
        axes[i, c].set_title(f"Kernel {i+1}, Channel {c+1}")
plt.tight_layout()
plt.savefig("conv_kernels.png")
plt.show()

5.3 可视化 2：看特征图是什么效果

卷积+ReLU 后的特征图是 CNN "看到的东西"，咱们画前8张特征图：

python 复制代码

# 提取第一张特征图（Batch=1，取第0个）
feat_map_np = feat_map[0].cpu().numpy()  # 形状：[16, 32, 32]

# 画前8张特征图
fig, axes = plt.subplots(2, 4, figsize=(12, 6))
axes = axes.flatten()
for i in range(8):
    img = feat_map_np[i]
    # 归一化显示
    img = (img - img.min()) / (img.max() - img.min())
    axes[i].imshow(img, cmap='gray')
    axes[i].axis('off')
    axes[i].set_title(f"Feature Map {i+1}")
plt.tight_layout()
plt.savefig("feature_maps.png")
plt.show()

✅ 直观结论：不同特征图对应不同的 "滤镜效果" ------ 有的亮区集中在中间，有的集中在边缘，这就是 CNN 提取的 "局部特征"。

6. 面试避坑指南 (Interview Q&A)

结合算法岗高频面试题，咱们按"新手能听懂、面试官满意"的思路整理，直接背！

Q1：1×1 卷积有什么用？（高频中的高频）

1×1 卷积看似 "只看一个像素"，实则是 CNN 的 "降维神器"，核心作用有两个：

降维/升维：在不改变特征图长宽的前提下，调整通道数。比如用 1×1 卷积把 64 通道的特征图降到 16 通道，参数量只有 64×16×1×1=1024 个，比 3×3 卷积高效得多；

实现跨通道交互：替代全连接层，在保持空间结构的同时完成通道维度的特征融合。

Q2：卷积层和全连接层的核心区别？

核心区别在"连接方式"和"参数量"：

全连接层（FC）：全局连接，每个输出节点和所有输入节点相连，参数量爆炸，且不具备平移不变性（数字 "8" 移到右边，MLP 就认不出来了）；

卷积层（Conv）：局部连接 + 权值共享，参数量只有全连接层的几百分之一，且因为权值共享，不管物体在图片的哪个位置，卷积核都能识别 ------ 天然具备平移不变性，适合处理图像。

Q3：感受野（Receptive Field）是什么？怎么计算？（笔试必考）

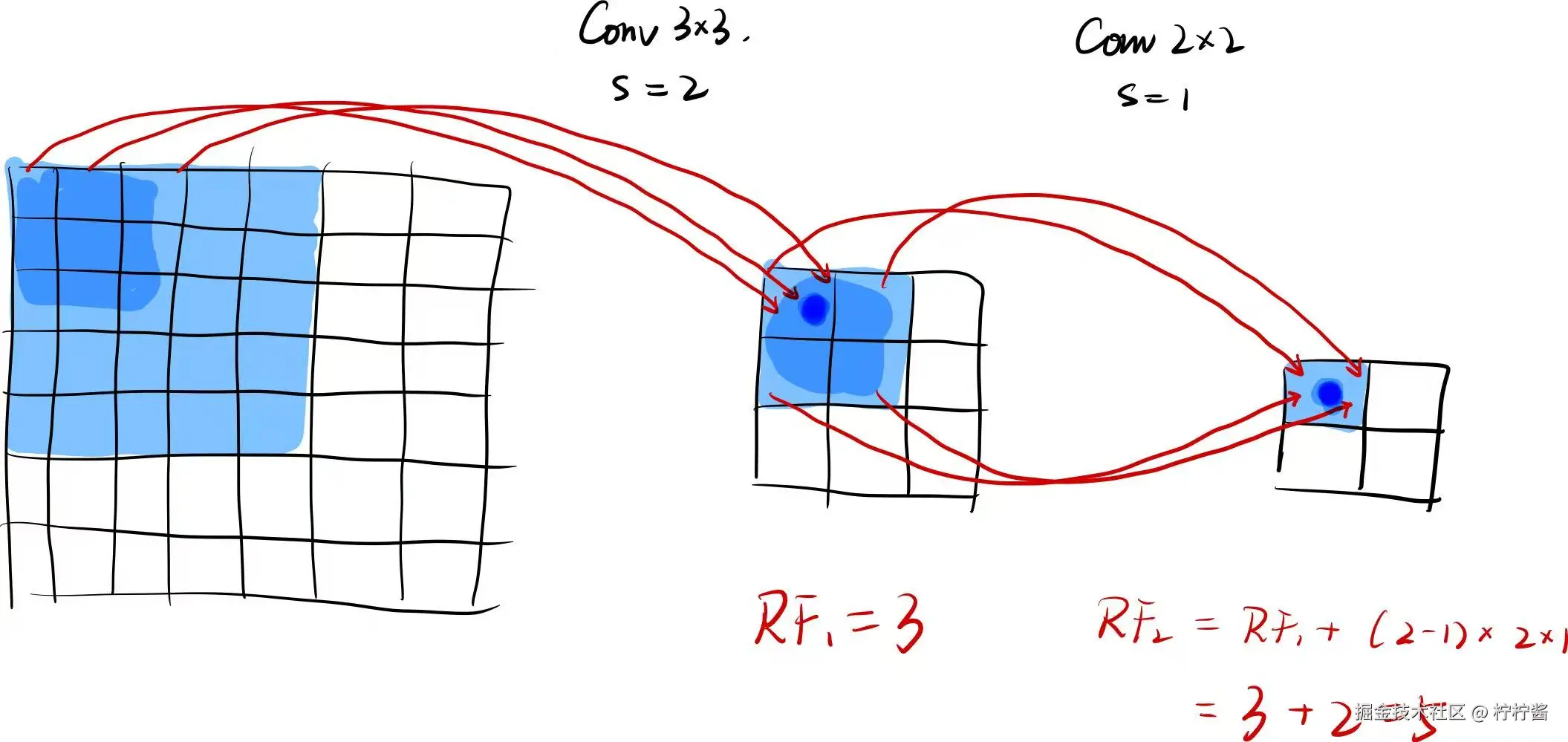
感受野 是卷积神经网络（CNN） 中的核心概念，指的是：特征图上的一个像素点，对应输入图像的区域范围 。简单来说，特征图里的每个像素，都是由输入图像中一块固定区域的像素计算而来，这块区域就是这个特征点的感受野。感受野的大小会随着网络层数增加而扩大，这也是CNN能从局部特征（如边缘、纹理）逐步提取全局特征（如物体轮廓、类别）的关键。
在单层卷积的基础上，叠加第二层卷积，就能直观看到感受野如何变大。多层卷积的感受野需要递归计算，公式如下：

<math xmlns="http://www.w3.org/1998/Math/MathML"> R F n = R F n − 1 + ( k n − 1 ) × ∏ i = 1 n − 1 s i RF_n = RF_{n-1} + (k_n - 1) \times \prod_{i=1}^{n-1} s_i </math>RFn=RFn−1+(kn−1)×∏i=1n−1si

其中：

<math xmlns="http://www.w3.org/1998/Math/MathML"> R F n RF_n </math>RFn：第 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n层的感受野大小

<math xmlns="http://www.w3.org/1998/Math/MathML"> k n k_n </math>kn：第 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n层的卷积核大小

<math xmlns="http://www.w3.org/1998/Math/MathML"> s n s_n </math>sn：第 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n层的步幅

<math xmlns="http://www.w3.org/1998/Math/MathML"> R F 1 = k 1 RF_1 = k_1 </math>RF1=k1：第一层感受野等于卷积核大小

Q4：池化层可以用卷积层替代吗？（进阶题）

可以！用 stride=2 的卷积层（比如 3×3, stride=2, padding=1）替代 MaxPool2d，效果甚至更好：

① 替代逻辑：stride=2 的卷积层能实现"下采样+特征提取"，而池化层只有下采样，没有特征提取；

② 实战场景：现代 CNN（比如 ResNet）几乎不用池化层，而是用 stride=2 的卷积层做下采样，减少特征丢失。

Q5：padding 的作用有哪些？（基础题）

核心作用有两个：

① 保持输出尺寸：避免图片 "越卷越小" （比如 Same Padding 让卷积前后尺寸不变）；

② 保留边缘特征：不 padding 的话，图片边缘的像素只会被卷积核扫 1 次，内部像素被扫多次，边缘特征容易丢失 ------ padding 让边缘像素和内部像素被扫的次数一致，保留更多边缘信息。

总结

CNN 对比 MLP 的核心优势是 "局部连接 + 权值共享"，既保留空间特征，又大幅减少参数量；
卷积层关键参数要记牢：Same Padding 公式 padding=(K-1)//2，维度计算公式是面试必背；
池化层核心作用是降维和提升鲁棒性，实战中优先用 MaxPool2d，且避免过度池化；
特征可视化是理解 CNN 的关键，能直观看到卷积核和特征图的效果，面试中提这个会加分。

📌 下期预告

卷积和池化的"兵器"已经磨好，维度计算、特征可视化也吃透了 ------ 是时候离开 MNIST 这个 "新手村"，挑战更复杂的 CIFAR-10 了！下一篇，我会手把手教你把今天的 CNN 积木块搭建成完整的分类网络，从数据集加载、网络搭建、训练调参，到特征图可视化、过拟合解决，全程用 MATLAB 老鸟能懂的逻辑拆解；总结 CNN 调参的核心技巧，让你不仅能跑通 CIFAR-10，还能把这套思路迁移到真实的图像分类场景中！

欢迎关注我的专栏，见证 MATLAB 老鸟到算法工程师的进阶之路！