考研线代第三课：向量组

文章目录

• 一、向量的概念与基本运算
• • [1. 向量的代数定义](#1. 向量的代数定义)
  • [2. 向量的基本运算](#2. 向量的基本运算)
• 二、向量内积与正交性
• • [1. 内积（点积）的定义](#1. 内积（点积）的定义)
  • [2. 内积的性质](#2. 内积的性质)
  • [3. 正交与模长](#3. 正交与模长)
  • • （1）模长（范数）
    • （2）正交相关定义
  • [4. 正交矩阵](#4. 正交矩阵)
• 三、向量组的线性关系
• • [1. 线性组合与线性表示](#1. 线性组合与线性表示)
  • [2. 线性相关与线性无关](#2. 线性相关与线性无关)
  • • （1）定义
    • （2）方程组视角
    • （3）易错点总结
  • [3. 线性相关性判别定理](#3. 线性相关性判别定理)
• 四、向量组的秩与极大线性无关组
• • [1. 极大线性无关组](#1. 极大线性无关组)
  • • （1）定义
    • （2）关键性质
  • [2. 向量组的秩](#2. 向量组的秩)
  • • （1）定义与几何意义
    • （2）重要结论
    • （3）极大无关组求解步骤
• [五、等价矩阵 vs 等价向量组](#五、等价矩阵 vs 等价向量组)
• • [1. 等价矩阵](#1. 等价矩阵)
  • [2. 等价向量组](#2. 等价向量组)
  • [3. 二者区别](#3. 二者区别)
• 六、向量空间（数一）
• • [1. 基本概念](#1. 基本概念)
  • [2. 基变换与坐标变换](#2. 基变换与坐标变换)
  • • （1）基变换与过渡矩阵
    • （2）坐标变换公式
    • （3）施密特正交化（规范正交基构造）

---

一、向量的概念与基本运算

1. 向量的代数定义

n 维向量是由 n 个实数构成的有序数组，分为两种形式：

• 行向量： α T = ( a 1 , a 2 , . . . , a n ) \boldsymbol{\alpha^T} = (a_1, a_2, ..., a_n) αT=(a1,a2,...,an)（横向排列，本质是 1×n 矩阵）

• 列向量： α = ( a 1 a 2 . . . a n ) \boldsymbol{\alpha} = \begin{pmatrix} a_1 \\ a_2 \\ ... \\ a_n \end{pmatrix} α= a1a2...an （纵向排列，本质是 n×1 矩阵）

注：行向量与列向量是 "互为转置" 的关系，在运算中需注意维度匹配（如行向量 × 列向量可求内积，列向量 × 行向量得到秩 1 矩阵）。

2. 向量的基本运算

相等 ：两个向量相等    ⟺    \iff ⟺ 同型（同为行 / 列向量且维度相同）且对应分量完全相同。

例： ( 1 , 2 ) ≠ ( 1 , 2 , 3 ) (1,2) \neq (1,2,3) (1,2)=(1,2,3)（不同维）； ( 1 , 2 ) ≠ ( 2 , 1 ) (1,2) \neq (2,1) (1,2)=(2,1)（分量不同）。

加法：同型向量对应分量相加，即

α + β = ( a 1 + b 1 , a 2 + b 2 , . . . , a n + b n ) \boldsymbol{\alpha} + \boldsymbol{\beta} = (a_1+b_1, a_2+b_2, ..., a_n+b_n) α+β=(a1+b1,a2+b2,...,an+bn)

（性质：交换律、结合律，零向量是加法单位元）

数乘 ：常数 k k k乘向量的每个分量，即

k α = ( k a 1 , k a 2 , . . . , k a n ) k\boldsymbol{\alpha} = (ka_1, ka_2, ..., ka_n) kα=(ka1,ka2,...,kan)

（几何意义： k > 0 k>0 k>0 时同向伸缩， k < 0 k<0 k<0 时反向伸缩， ∣ k ∣ > 1 |k|>1 ∣k∣>1 伸长， ∣ k ∣ < 1 |k|<1 ∣k∣<1 缩短）

二、向量内积与正交性

1. 内积（点积）的定义

对 n 维向量 α = ( a 1 , . . . , a n ) \boldsymbol{\alpha} = (a_1,...,a_n) α=(a1,...,an) 和 β = ( b 1 , . . . , b n ) \boldsymbol{\beta} = (b_1,...,b_n) β=(b1,...,bn)，内积定义为：

⟨ α , β ⟩ = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = \sum_{i=1}^{n} a_i b_i = a_1 b_1 + a_2 b_2 + \dots + a_n b_n ⟨α,β⟩=∑i=1naibi=a1b1+a2b2+⋯+anbn

• 列向量 ：若 α \boldsymbol{\alpha} α 和 β \boldsymbol{\beta} β 为 n×1 列向量，内积为 ⟨ α , β ⟩ = α T β \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = \boldsymbol{\alpha}^T \boldsymbol{\beta} ⟨α,β⟩=αTβ

• 行向量 ：若 α \boldsymbol{\alpha} α 和 β \boldsymbol{\beta} β 为 1×n 行向量，内积为 ⟨ α , β ⟩ = α β T \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = \boldsymbol{\alpha} \boldsymbol{\beta}^T ⟨α,β⟩=αβT

无论向量类型，内积结果均为实数（1×1 矩阵）。

2. 内积的性质

1. 正定性 ： ⟨ α , α ⟩ = ∑ i = 1 n a i 2 = ∣ ∣ α ∣ ∣ 2 ≥ 0 \langle \boldsymbol{\alpha}, \boldsymbol{\alpha} \rangle =\sum\limits_{i=1}^{n} a_i^2=||\boldsymbol{\alpha}||^2\geq 0 ⟨α,α⟩=i=1∑nai2=∣∣α∣∣2≥0，当且仅当 α = 0 \boldsymbol{\alpha} = \boldsymbol{0} α=0 时等号成立。

2. 对称性 ： ⟨ α , β ⟩ = ⟨ β , α ⟩ = ∣ ∣ α ∣ ∣ ⋅ ∣ ∣ β ∣ ∣ cos ⁡ θ \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = \langle \boldsymbol{\beta}, \boldsymbol{\alpha} \rangle=||\boldsymbol{\alpha}|| \cdot ||\boldsymbol{\beta}||\cos{\theta} ⟨α,β⟩=⟨β,α⟩=∣∣α∣∣⋅∣∣β∣∣cosθ（ θ \theta θ 为两向量夹角）。

3. 线性性：

   ⟨ k α , β ⟩ = k ⟨ α , β ⟩ \langle k\boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = k\langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle ⟨kα,β⟩=k⟨α,β⟩；

   ⟨ α + γ , β ⟩ = ⟨ α , β ⟩ + ⟨ γ , β ⟩ \langle \boldsymbol{\alpha} + \boldsymbol{\gamma}, \boldsymbol{\beta} \rangle = \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle + \langle \boldsymbol{\gamma}, \boldsymbol{\beta} \rangle ⟨α+γ,β⟩=⟨α,β⟩+⟨γ,β⟩。

3. 正交与模长

（1）模长（范数）

向量 α \boldsymbol{\alpha} α 的 L2 范数（几何长度）：

∥ α ∥ = ⟨ α , α ⟩ = ∑ i = 1 n a i 2 \|\boldsymbol{\alpha}\| = \sqrt{\langle \boldsymbol{\alpha}, \boldsymbol{\alpha} \rangle} = \sqrt{\sum\limits_{i=1}^n{a_i}^2} ∥α∥=⟨α,α⟩ =i=1∑nai2

• 单位向量：模长为1的向量，非零向量可单位化为 α 0 = α ∣ ∣ α ∣ ∣ \boldsymbol{\alpha}^0 = \frac{\boldsymbol{\alpha}}{||\boldsymbol{\alpha}||} α0=∣∣α∣∣α。
• 维度特性：二维空间中，与某向量正交的单位向量有 2 个；三维及以上维度中，正交单位向量构成对应子空间。

⚠️ 注意区分：

• ∣ A ∣ |A| ∣A∣：矩阵 A A A的行列式（标量，反映矩阵 "体积" 或 "可逆性"）。

• ∣ ∣ A ∣ ∣ ||A|| ∣∣A∣∣：矩阵 A A A的范数（衡量矩阵大小的方式，如 Frobenius 范数、谱范数等）。

二者背景不同：行列式侧重代数性质，范数侧重几何性质或大小度量。

（2）正交相关定义

向量正交 ：若 ⟨ α , β ⟩ = 0 \langle \boldsymbol{\alpha}, \boldsymbol{\beta} \rangle = 0 ⟨α,β⟩=0，则 α \boldsymbol{\alpha} α 与 β \boldsymbol{\beta} β 正交（几何意义：垂直）。

例： α = ( 1 , 0 ) T \boldsymbol{\alpha}=(1,0)^T α=(1,0)T 与 β = ( 0 , 1 ) T \boldsymbol{\beta}=(0,1)^T β=(0,1)T 正交（内积 = 0）。

正交向量组 ：两两正交的非零向量组，即对 { α 1 , . . . , α m } \{\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_m\} {α1,...,αm}，满足 ⟨ α i , α j ⟩ = 0 \langle \boldsymbol{\alpha}_i, \boldsymbol{\alpha}_j \rangle = 0 ⟨αi,αj⟩=0（ i ≠ j i \neq j i=j） 且 α i ≠ 0 \boldsymbol{\alpha}_i \neq \boldsymbol{0} αi=0（ i = 1 , . . . , m i=1,...,m i=1,...,m）。

规范正交基 ：正交且单位化的向量组，满足 ⟨ α i , α j ⟩ = { 1 ( i = j ) 0 ( i ≠ j ) \langle \boldsymbol{\alpha}_i, \boldsymbol{\alpha}_j \rangle = \begin{cases} 1 & (i=j) \\ 0 & (i \neq j) \end{cases} ⟨αi,αj⟩={10(i=j)(i=j)

例： R 3 \mathbb{R}^3 R3 的标准基 { ( 1 , 0 , 0 ) T , ( 0 , 1 , 0 ) T , ( 0 , 0 , 1 ) T } \{(1,0,0)^T, (0,1,0)^T, (0,0,1)^T\} {(1,0,0)T,(0,1,0)T,(0,0,1)T}。

4. 正交矩阵

定义 ：n 阶实矩阵 A A A 满足 A T A = E A^\mathrm{T} A = E ATA=E（等价于 A − 1 = A T A^{-1} = A^\mathrm{T} A−1=AT，正交矩阵必可逆）。

核心性质：

1. 行/列向量组均为规范正交基；
2. 行列式 ∣ A ∣ = ± 1 |A| = \pm 1 ∣A∣=±1；
3. 几何意义：对应保距变换（旋转、反射等，保持内积和长度不变）。

三、向量组的线性关系

1. 线性组合与线性表示

线性组合 ：对向量组 S = { α 1 , . . . , α m } S = \{\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_m\} S={α1,...,αm}，形如 k 1 α 1 + . . . + k m α m k_1\boldsymbol{\alpha}_1 + ... + k_m\boldsymbol{\alpha}_m k1α1+...+kmαm（ k i k_i ki 为实数）的向量称为 S S S 的线性组合。

线性表示 ：若 β = k 1 α 1 + . . . + k m α m \boldsymbol{\beta} = k_1\boldsymbol{\alpha}_1 + ... + k_m\boldsymbol{\alpha}_m β=k1α1+...+kmαm，则 β \boldsymbol{\beta} β 可由 S S S 线性表示， ( k 1 , . . . , k m ) (k_1,...,k_m) (k1,...,km) 为表示系数（系数不唯一    ⟺    S \iff S ⟺S 线性相关）。

2. 线性相关与线性无关

向量组的相关性是 "非黑即白" 的 ------ 要么相关（含 "多余" 向量），要么无关（全 "独立"），无中间状态。

（1）定义

线性相关 ：存在不全为 0 的常数 k 1 , . . . , k m k_1,...,k_m k1,...,km，使 k 1 α 1 + . . . + k m α m = 0 k_1\boldsymbol{\alpha}_1 + ... + k_m\boldsymbol{\alpha}_m = \boldsymbol{0} k1α1+...+kmαm=0。

（意义：组中至少一个向量可由其余向量表示，存在 "多余" 向量）

线性无关 ：仅当 k 1 = . . . = k m = 0 k_1=...=k_m=0 k1=...=km=0 时， k 1 α 1 + . . . + k m α m = 0 k_1\boldsymbol{\alpha}_1 + ... + k_m\boldsymbol{\alpha}_m = \boldsymbol{0} k1α1+...+kmαm=0 成立。

（意义：所有向量 "独立"，任一向量不能由其余表示）

（2）方程组视角

设矩阵 A = ( α 1 , . . . , α m ) A = (\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_m) A=(α1,...,αm)（列向量构成）：

• 线性相关    ⟺    \iff ⟺ 齐次方程组 A x = 0 A\boldsymbol{x} = \boldsymbol{0} Ax=0 有非零解    ⟺    r ( A ) < m \iff r(A) < m ⟺r(A)<m；

• 线性无关    ⟺    \iff ⟺ 齐次方程组 A x = 0 A\boldsymbol{x} = \boldsymbol{0} Ax=0 仅有零解    ⟺    r ( A ) = m \iff r(A) = m ⟺r(A)=m。

维度推论：

• n < m n<m n<m（方程数 < 未知数个数）：齐次线性方程组必有非零解，故 n+1 个 n 维向量必线性相关；

• n = m n=m n=m ：行列式 ∣ A ∣ = 0    ⟺    |A|=0 \iff ∣A∣=0⟺ 非零解（相关）； ∣ A ∣ ≠ 0    ⟺    |A| \neq 0 \iff ∣A∣=0⟺ 零解（无关）；

• n > m n>m n>m ：无"方程数<未知数个数"的约束，需直接判断秩与向量个数的关系。

（3）易错点总结

1. 单个向量：非零向量线性无关，零向量线性相关；

2. 含零向量的组：必线性相关（取零向量系数为 1，其余为 0 即可）；

3. 部分与整体：

   • 部分相关    ⟹    \implies ⟹ 整体相关；

   • 整体无关    ⟹    \implies ⟹ 部分无关。

   { α 1 , . . . , α s } \{\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s\} {α1,...,αs} 线性无关，说明这 m 个向量张成 m 维空间，那么即使去掉 n (n<m) 个向量，剩下的 m-n 个向量依然张成 m-n 维空间，即这 m-n 个向量线性无关。

这是向量组中向量的++个数变化++ 的性质，注意与下方向量组中++维度变化++性质作区分。

• 个数变化：{(1,0),(0,1)} -> {(1,0),(0,1),(1,1)}（添加向量导致相关）；

• 维度变化：{(1,0),(0,1)} -> {(1,0,1),(0,1,0)} （升维后仍无关）。

3. 线性相关性判别定理

1. 若 S = { α 1 , . . . , α m } S = \{\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_m\} S={α1,...,αm} 线性无关，且 S ∪ { β } S \cup \{\boldsymbol{\beta}\} S∪{β} 线性相关，则 β \boldsymbol{\beta} β 可由 S S S 唯一线性表示。

2. "以少表多，多的必相关"：若 { β 1 , . . . , β t } \{\boldsymbol{\beta}_1,..., \boldsymbol{\beta}_t\} {β1,...,βt} 可由 { α 1 , . . . , α s } \{\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s\} {α1,...,αs} 线性表示，且 t > s t > s t>s，则 { β 1 , . . . , β t } \{\boldsymbol{\beta}_1,..., \boldsymbol{\beta}_t\} {β1,...,βt} 线性相关。

   其等价命题：若 { β 1 , . . . , β t } \{\boldsymbol{\beta}_1,..., \boldsymbol{\beta}_t\} {β1,...,βt} 可由 { α 1 , . . . , α s } \{\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s\} {α1,...,αs} 线性表示，且 { β 1 , . . . , β t } \{\boldsymbol{\beta}_1,..., \boldsymbol{\beta}_t\} {β1,...,βt} 线性无关，则 t ≤ s t \leq s t≤s。

   高维空间能表示低维空间，低维空间不能表示高维空间。

3. 向量 β \boldsymbol{\beta} β 可由 { α 1 , . . . , α s } \{\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s\} {α1,...,αs} 线性表示    ⟺    \iff ⟺ 非齐次方程组 A x = β A\boldsymbol{x}=\boldsymbol{\beta} Ax=β（ A = ( α 1 , . . . , α s ) A=(\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s) A=(α1,...,αs)）有解    ⟺    r ( A ) = r ( [ A , β ] ) \iff r(A) = r([A, \boldsymbol{\beta}]) ⟺r(A)=r([A,β])（系数矩阵秩 = 增广矩阵秩）。

   向量 β \boldsymbol{\beta} β 不能由 { α 1 , . . . , α s } \{\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s\} {α1,...,αs} 线性表示    ⟺    \iff ⟺ 非齐次方程组 A x = β A\boldsymbol{x}=\boldsymbol{\beta} Ax=β（ A = ( α 1 , . . . , α s ) A=(\boldsymbol{\alpha}_1,..., \boldsymbol{\alpha}_s) A=(α1,...,αs)）无解    ⟺    r ( A ) + 1 = r ( [ A , β ] ) \iff r(A) +1= r([A, \boldsymbol{\beta}]) ⟺r(A)+1=r([A,β])。

4. 低维无关    ⟹    \implies ⟹ 高维无关（相同位置添加分量后仍无关）；高维相关    ⟹    \implies ⟹ 低维相关（去掉相同分量后仍相关）。比如 { ( 1 , 0 ) , ( 0 , 1 ) } \{(1,0),(0,1)\} {(1,0),(0,1)} 与 { ( 1 , 0 , 2 ) , ( 0 , 1 , 3 ) } \{(1,0,2),(0,1,3)\} {(1,0,2),(0,1,3)} .

5. n + 1 n+1 n+1 个 n 维向量必线性相关（方程个数 n n n < 未知数个数 n + 1 n+1 n+1，齐次方程组必有非零解）。

四、向量组的秩与极大线性无关组

1. 极大线性无关组

（1）定义

设向量组 S = { α 1 , . . . , α m } S = \{\boldsymbol{\alpha}1,..., \boldsymbol{\alpha}m\} S={α1,...,αm}，若部分组 S 0 = { α i 1 , . . . , α i r } S_0 = \{\boldsymbol{\alpha}{i_1}, ..., \boldsymbol{\alpha}{i_r}\} S0={αi1,...,αir} 满足：

1. S 0 S_0 S0 线性无关；

2. S S S 中任一向量可由 S 0 S_0 S0 线性表示（或： S 0 S_0 S0 添加 S S S 中其他向量后必相关）。

则称 S 0 S_0 S0 为 S S S 的极大线性无关组。

（2）关键性质

不唯一性 ：一个向量组可能有多个极大无关组（例： { ( 1 , 0 ) , ( 0 , 1 ) , ( 1 , 1 ) } \{(1,0),(0,1),(1,1)\} {(1,0),(0,1),(1,1)}的极大无关组可为 { ( 1 , 0 ) , ( 0 , 1 ) } \{(1,0),(0,1)\} {(1,0),(0,1)}或 { ( 1 , 0 ) , ( 1 , 1 ) } \{(1,0),(1,1)\} {(1,0),(1,1)}）。

个数唯一性：所有极大无关组的向量个数相同（即向量组的秩）。

等价性：向量组与其任一极大无关组等价（双向线性表示）。

特殊情况：全零向量组无极大无关组；线性无关向量组的极大无关组是其本身。

2. 向量组的秩

（1）定义与几何意义

定义 ：向量组的极大无关组所含向量的个数，记为 r ( S ) r(S) r(S) 或 r a n k ( S ) rank(S) rank(S)。全零向量组的秩为 0（无极大无关组）。

几何意义 ：秩是向量组 "张成空间" 的维数（ r = 1 r=1 r=1 张成直线， r = 2 r=2 r=2 张成平面， r = 3 r=3 r=3 张成 3 维空间）。

补充结论：伴随矩阵 A ∗ A^* A∗ 的秩规律（n 阶方阵）：

r ( A ∗ ) = { n , r ( A ) = n 1 , r ( A ) = n − 1 0 , r ( A ) ≤ n − 2 r(A^*) = \begin{cases} n, & r(A)=n \\ 1, & r(A)=n-1 \\ 0, & r(A)\leq n-2\end{cases} r(A∗)=⎩ ⎨ ⎧n,1,0,r(A)=nr(A)=n−1r(A)≤n−2

对应向量组： A ∗ A^* A∗ 行/列向量组， r ( A ∗ ) = n r(A^*)=n r(A∗)=n 时线性无关； r ( A ∗ ) = 1 r(A^*)=1 r(A∗)=1 时两两成比例； r ( A ∗ ) = 0 r(A^*)=0 r(A∗)=0 时全为零向量。

（2）重要结论

1. 三秩相等：矩阵的秩 = 其行向量组的秩 = 其列向量组的秩。
2. 初等行变换性质：设矩阵 A A A 经有限次初等行变换化为矩阵 B B B，则 A A A 与 B B B 的行向量组彼此等价，且两矩阵对应位置的列向量组具有一致的线性相关性（即同时线性相关或同时线性无关）；
3. 若向量组 B B B 可由向量组 A A A 表示，则 r ( B ) ≤ r ( A ) r(B) \leq r(A) r(B)≤r(A)。
4. 等价向量组的秩相等（反之未必成立）。

（3）极大无关组求解步骤

1. 将向量组按列构成矩阵 A A A；

2. 对 A A A 作初等行变换化为行最简形；

3. 非零行的首非零元所在列对应的原向量，即为极大无关组。

操作注记：

• 行向量组可转置为列向量组求解，或作初等列变换（效果等价）；
• 求解时仅能单一方向变换（仅行/仅列），不可混合变换；
• 秩唯一，极大无关组不唯一。

五、等价矩阵 vs 等价向量组

1. 等价矩阵

定义 ：矩阵 A A A 经有限次初等变换（行 / 列变换）可化为 B B B，则 A A A 与 B B B 等价，记为 A ≅ B A \cong B A≅B。

核心条件：

1. 同型：行数、列数分别相等（初等变换不改变维度）；

2. 秩相等 ： r ( A ) = r ( B ) r(A) = r(B) r(A)=r(B)（等价的充要条件）。

本质：反映 "初等变换下的结构相似"，即秩结构相同，可互相转化，但行 / 列向量组的生成能力未必相同。

A , B A,B A,B 同型时， A ≅ B    ⟺    r ( A ) = r ( B )    ⟺    P A Q = B A \cong B\iff r(A)=r(B)\iff PAQ=B A≅B⟺r(A)=r(B)⟺PAQ=B（ P , Q P,Q P,Q 是可逆矩阵）

2. 等价向量组

定义 ：向量组 ( I ) = { α 1 , . . . , α m } (I) = \{\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_m\} (I)={α1,...,αm} 与 ( I I ) = { β 1 , . . . , β k } (II) = \{\boldsymbol{\beta}_1, ..., \boldsymbol{\beta}_k\} (II)={β1,...,βk} 互相线性表示，记作 ( I ) ≅ ( I I ) (I) \cong (II) (I)≅(II)。

充要条件 ： r ( I ) = r ( I I ) r(I)=r(II) r(I)=r(II)，且可单方向表示。即 r ( I ) = r ( I I ) = r ( I , I I ) r(I)=r(II)=r(I,II) r(I)=r(II)=r(I,II)

本质：反映 "生成能力的信息等价"，即张成空间相同，有效信息维度一致。

等价向量组满足：

1. 反身性： ( I ) ≅ ( I ) (I) \cong (I) (I)≅(I)；
2. 对称性：若 ( I ) ≅ ( I I ) (I) \cong (II) (I)≅(II) ，则 ( I I ) ≅ ( I ) (II) \cong (I) (II)≅(I)；
3. 传递性：若 ( I ) ≅ ( I I ) , ( I I ) ≅ ( I I I ) (I) \cong (II),(II) \cong (III) (I)≅(II),(II)≅(III)，则 ( I ) ≅ ( I I I ) (I) \cong (III) (I)≅(III) .

向量组和它的极大线性无关组是等价向量组。

等价向量组的向量个数不一定相同。

3. 二者区别

矩阵等价针对同型矩阵，标准为初等变换可互化，反映矩阵整体结构的相似性；向量组等价针对同维向量组（可不同个数），标准为双向线性表示，反映向量组生成空间的一致性。

同秩是等价的必要非充分条件，同秩同型矩阵必等价，同秩向量组未必等价。

六、向量空间（数一）

1. 基本概念

n 维向量空间 R n \mathbb{R}^n Rn 中，若 { ε 1 , ... , ε n } \{\boldsymbol{\varepsilon}_1, \dots, \boldsymbol{\varepsilon}_n\} {ε1,...,εn} 线性无关，则任一 α ∈ R n \boldsymbol{\alpha} \in \mathbb{R}^n α∈Rn 可唯一表示为：

α = x 1 ε 1 + ⋯ + x n ε n \boldsymbol{\alpha} = x_1\boldsymbol{\varepsilon}_1 + \dots + x_n\boldsymbol{\varepsilon}_n α=x1ε1+⋯+xnεn

• 基：有序线性无关向量组 { ε 1 , ... , ε n } \{\boldsymbol{\varepsilon}_1, \dots, \boldsymbol{\varepsilon}_n\} {ε1,...,εn}；
• 维数：基向量的个数 n n n；
• 坐标： [ x 1 , ... , x n ] [x_1, \dots, x_n] [x1,...,xn]（行）或 [ x 1 , ... , x n ] T [x_1, \dots, x_n]^\mathrm{T} [x1,...,xn]T（列），即 α \boldsymbol{\alpha} α 在该基下的坐标。

几何理解：二维平面中，任意两个线性无关（不平行）的向量均可作为基，垂直仅是特殊情况。

2. 基变换与坐标变换

（1）基变换与过渡矩阵

设 R n \mathbb{R}^n Rn 的两组基：

• 旧基： B 1 = { ε 1 , . . . , ε n } B_1 = \{\boldsymbol{\varepsilon}_1, ..., \boldsymbol{\varepsilon}_n\} B1={ε1,...,εn}；

• 新基： B 2 = { η 1 , . . . , η n } B_2 = \{\boldsymbol{\eta}_1, ..., \boldsymbol{\eta}_n\} B2={η1,...,ηn}。

新基中每个向量可由旧基线性表示：

{ η 1 = p 11 ε 1 + . . . + p n 1 ε n η 2 = p 12 ε 1 + . . . + p n 2 ε n ⋮ η n = p 1 n ε 1 + . . . + p n n ε n \begin{cases} \boldsymbol{\eta}1 = p{11}\boldsymbol{\varepsilon}1 + ... + p{n1}\boldsymbol{\varepsilon}_n \\ \boldsymbol{\eta}2 = p{12}\boldsymbol{\varepsilon}1 + ... + p{n2}\boldsymbol{\varepsilon}_n \\ \vdots \\ \boldsymbol{\eta}n = p{1n}\boldsymbol{\varepsilon}1 + ... + p{nn}\boldsymbol{\varepsilon}_n \end{cases} ⎩ ⎨ ⎧η1=p11ε1+...+pn1εnη2=p12ε1+...+pn2εn⋮ηn=p1nε1+...+pnnεn

矩阵形式（基变换公式）：

( η 1 , . . . , η n ) = ( ε 1 , . . . , ε n ) P (\boldsymbol{\eta}_1, ..., \boldsymbol{\eta}_n) = (\boldsymbol{\varepsilon}_1, ..., \boldsymbol{\varepsilon}_n) P (η1,...,ηn)=(ε1,...,εn)P

其中 P = ( p i j ) n × n P = (p_{ij})_{n×n} P=(pij)n×n 称为从旧基 B 1 B_1 B1 到新基 B 2 B_2 B2 的过渡矩阵（必可逆，因新基线性无关）。

（2）坐标变换公式

设 α \boldsymbol{\alpha} α 在旧基 B 1 B_1 B1 下的坐标为 X = ( x 1 , . . . , x n ) T \boldsymbol{X} = (x_1, ..., x_n)^T X=(x1,...,xn)T，即 α = ( ε 1 , . . . , ε n ) X \boldsymbol{\alpha} = (\boldsymbol{\varepsilon}_1, ..., \boldsymbol{\varepsilon}_n) \boldsymbol{X} α=(ε1,...,εn)X；在新基 B 2 B_2 B2 下的坐标为 Y = ( y 1 , . . . , y n ) T \boldsymbol{Y} = (y_1, ..., y_n)^T Y=(y1,...,yn)T，即 α = ( η 1 , . . . , η n ) Y \boldsymbol{\alpha} = (\boldsymbol{\eta}_1, ..., \boldsymbol{\eta}_n) \boldsymbol{Y} α=(η1,...,ηn)Y。

结合基变换公式，得：

( ε 1 , . . . , ε n ) X = ( ε 1 , . . . , ε n ) P Y (\boldsymbol{\varepsilon}_1, ..., \boldsymbol{\varepsilon}_n) \boldsymbol{X} = (\boldsymbol{\varepsilon}_1, ..., \boldsymbol{\varepsilon}_n) P \boldsymbol{Y} (ε1,...,εn)X=(ε1,...,εn)PY

因旧基矩阵可逆，故坐标变换公式：

X = P Y 或 Y = P − 1 X \boldsymbol{X} = P \boldsymbol{Y} \quad \text{或} \quad \boldsymbol{Y} = P^{-1} \boldsymbol{X} X=PY或Y=P−1X

（旧坐标求新坐标用 Y = P − 1 X \boldsymbol{Y} = P^{-1} \boldsymbol{X} Y=P−1X；新坐标求旧坐标用 X = P Y \boldsymbol{X} = P \boldsymbol{Y} X=PY）。

（3）施密特正交化（规范正交基构造）

对线性无关向量组 { α 1 , . . . , α r } \{\boldsymbol{\alpha}_1, ..., \boldsymbol{\alpha}_r\} {α1,...,αr}，构造正交向量组 { β 1 , . . . , β r } \{\boldsymbol{\beta}_1, ..., \boldsymbol{\beta}_r\} {β1,...,βr}：

• 步骤1：正交化

β 1 = α 1 β 2 = α 2 − ⟨ α 2 , β 1 ⟩ ⟨ β 1 , β 1 ⟩ β 1 ⋮ β r = α r − ∑ i = 1 r − 1 ⟨ α r , β i ⟩ ⟨ β i , β i ⟩ β i \boldsymbol{\beta}_1 = \boldsymbol{\alpha}_1\\ \boldsymbol{\beta}_2 = \boldsymbol{\alpha}_2 - \frac{\langle \boldsymbol{\alpha}_2, \boldsymbol{\beta}_1 \rangle}{\langle \boldsymbol{\beta}_1, \boldsymbol{\beta}_1 \rangle} \boldsymbol{\beta}_1\\ \vdots\\ \boldsymbol{\beta}_r = \boldsymbol{\alpha}r - \sum{i=1}^{r-1} \frac{\langle \boldsymbol{\alpha}_r, \boldsymbol{\beta}_i \rangle}{\langle \boldsymbol{\beta}_i, \boldsymbol{\beta}_i \rangle} \boldsymbol{\beta}_i\\ β1=α1β2=α2−⟨β1,β1⟩⟨α2,β1⟩β1⋮βr=αr−i=1∑r−1⟨βi,βi⟩⟨αr,βi⟩βi

• 步骤2：单位化

γ i = β i ∥ β i ∥ ( i = 1 , . . . , r ) \boldsymbol{\gamma}_i = \frac{\boldsymbol{\beta}_i}{\|\boldsymbol{\beta}_i\|} \quad (i=1,...,r) γi=∥βi∥βi(i=1,...,r)

则 { γ 1 , . . . , γ r } \{\boldsymbol{\gamma}_1, ..., \boldsymbol{\gamma}_r\} {γ1,...,γr} 为规范正交组。

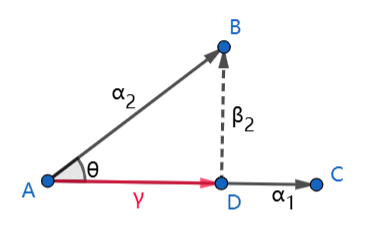
• 几何解释

  以 β 2 \beta_2 β2 为例，从向量 α 2 \alpha_2 α2 向向量 α 1 \alpha_1 α1 作垂线，得向量 r r r ，则向量 r r r 的长度为 ∣ ∣ α 2 ∣ ∣ cos ⁡ θ ||\alpha_2||\cos{\theta} ∣∣α2∣∣cosθ，方向为 α 1 ∣ ∣ α 1 ∣ ∣ \frac{\alpha_1}{||\alpha_1||} ∣∣α1∣∣α1，故向量

r = ∣ ∣ α 2 ∣ ∣ cos ⁡ θ ⋅ α 1 ∣ ∣ α 1 ∣ ∣ = ∣ ∣ α 1 ∣ ∣ ⋅ ∣ ∣ α 2 ∣ ∣ cos ⁡ θ ⋅ α 1 ∣ ∣ α 1 ∣ ∣ 2 = ⟨ α 1 , α 2 ⟩ ⋅ α 1 ⟨ α 1 , α 1 ⟩ = ⟨ α 1 , α 2 ⟩ ⟨ α 1 , α 1 ⟩ ⋅ α 1 = ⟨ β 1 , α 2 ⟩ ⟨ β 1 , β 1 ⟩ ⋅ β 1 \begin{align*} r&=||\alpha_2||\cos{\theta}\cdot\frac{\alpha_1}{||\alpha_1||}\\&= ||\alpha_1||\cdot||\alpha_2||\cos{\theta}\cdot\frac{\alpha_1}{||\alpha_1||^2}\\&= \langle \alpha_1, \alpha_2 \rangle\cdot\frac{\alpha_1}{\langle \alpha_1, \alpha_1 \rangle}\\&= \frac{\langle \alpha_1, \alpha_2 \rangle}{\langle \alpha_1, \alpha_1 \rangle}\cdot\alpha_1\\&= \frac{\langle \beta_1, \alpha_2 \rangle}{\langle \beta_1, \beta_1 \rangle}\cdot\beta_1 \end{align*} r=∣∣α2∣∣cosθ⋅∣∣α1∣∣α1=∣∣α1∣∣⋅∣∣α2∣∣cosθ⋅∣∣α1∣∣2α1=⟨α1,α2⟩⋅⟨α1,α1⟩α1=⟨α1,α1⟩⟨α1,α2⟩⋅α1=⟨β1,β1⟩⟨β1,α2⟩⋅β1

又三角形法则 β 2 = α 2 − r = α 2 − ⟨ β 1 , α 2 ⟩ ⟨ β 1 , β 1 ⟩ ⋅ β 1 \beta_2=\alpha_2-r=\alpha_2-\frac{\langle \beta_1, \alpha_2 \rangle}{\langle \beta_1, \beta_1 \rangle}\cdot\beta_1 β2=α2−r=α2−⟨β1,β1⟩⟨β1,α2⟩⋅β1