3dgs学习有感

文章目录

• • 3dg中使用的图形学一些细节
  • • 3dgs中涉及的坐标系变换
    • 一些普及知识
    • 投影变化矩阵由来
    • • 变换到NDT的范围为[-1,1]，相机坐标系是右手坐标系（x右侧，y轴上侧，z轴指向与相机看向方向相反（物体的z轴坐标为负数））
      • 变换到NDT的范围为[0,1]，3dgs中定义投影矩阵所使用的
      • [透射投影变换后NDT中的齐次坐标 ( x c , y c , z c , w c ) (x_c, y_c, z_c, w_c) (xc,yc,zc,wc)中的 w c w_c wc都要求是正值原因](#透射投影变换后NDT中的齐次坐标 ( x c , y c , z c , w c ) (x_c, y_c, z_c, w_c) (xc,yc,zc,wc)中的 w c w_c wc都要求是正值原因)
  • 3dgs整个项目的系统流程

3dg中使用的图形学一些细节

3dgs中涉及的坐标系变换

完整的 3DGS 渲染流程是：

世界空间 → world_view_transform → 相机空间

相机空间 → projection_matrix → 裁剪空间

裁剪空间 → 透视除法 → 标准化设备坐标

NDC → 视口变换 → 屏幕像素坐标

#在camera.py文件主要存储了三种主要变换矩阵

#W2C（世界坐标系到相机坐标系的变换）
self.world_view_transform = torch.tensor(getWorld2View2(R, T, trans, scale)).transpose(0, 1).cuda()
#C2裁剪空间（世界坐标系到裁剪空间坐标系的变换）
self.projection_matrix = getProjectionMatrix(znear=self.znear, zfar=self.zfar, fovX=self.FoVx, fovY=self.FoVy).transpose(0,1).cuda()
#W2裁剪空间
self.full_proj_transform = (self.world_view_transform.unsqueeze(0).bmm(self.projection_matrix.unsqueeze(0))).squeeze(0)

一些普及知识

• OpenGL（经典右手系） ：相机看向 -z 方向 。在观察空间中，近平面位于 z = − n z = -n z=−n，远平面位于 z = − f z = -f z=−f（ n , f > 0 n, f > 0 n,f>0）。

  NDC 的 z 范围传统是 [-1, 1]，映射后近平面对应-1，远平面对应 1。

• Direct3D（左手系） ：相机看向 +z 方向 。在观察空间中，近平面在 z = n z = n z=n，远平面在 z = f z = f z=f（ n , f > 0 n, f > 0 n,f>0）。

  NDC 的 z 范围是 [0, 1]，映射后近平面对应 0，远平面对应 1。（3dgs中使用的）

投影变化矩阵由来

分别由透视投影矩阵（压缩成为长方体）和正交投影矩阵（它通常将一个定义在三维空间中的长方体视锥体（View Frustum由 l e f t , r i g h t , b o t t o m , t o p , n e a r , f a r left, right, bottom, top, near, far left,right,bottom,top,near,far定义）变换为一个标准立方体），通常会为限制z在（0，w）或者（-w，w）范围里的长方体。
下面出现的参数含义说明：

• l , r l, r l,r：左 (Left) 和 右 (Right) 边界（ x x x 轴，近平面上的坐标值）。
• b , t b, t b,t：下 (Bottom) 和 上 (Top) 边界（ y y y 轴，近平面上的坐标值）。
• n , f n, f n,f：近 (Near) 和 远 (Far) 边界（ z z z 轴）。

一般NDT坐标系（下面两种情况，下面两种情况的相机坐标系有区别）就是左手坐标系（x指向右侧，y轴指向上面，z轴指向相机看向的地方（也就是相机看到的物体的z轴坐标都是正的））

变换到NDT的范围为[-1,1]，相机坐标系是右手坐标系（x右侧，y轴上侧，z轴指向与相机看向方向相反（物体的z轴坐标为负数））

透射投影矩阵如下：
P = [ n 0 0 0 0 n 0 0 0 0 n + f − f n 0 0 1 0 ] P = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n + f & -fn \\ 0 & 0 & 1 & 0 \end{bmatrix} P= n0000n0000n+f100−fn0

正交投影矩阵如下：T矩阵
M o r t h o = S ⋅ T = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] M_{ortho} = S \cdot T = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{bmatrix} Mortho=S⋅T= r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1 ，

其中平移矩阵 ( T T T)：

其目的是将长方体的中心点 ( r + l 2 , t + b 2 , n + f 2 ) (\frac{r+l}{2}, \frac{t+b}{2}, \frac{n+f}{2}) (2r+l,2t+b,2n+f) 移动到原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)。

T = [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] T = \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} T= 100001000010−2r+l−2t+b−2n+f1

缩放矩阵 ( S S S)：

其目的是将长方体的宽度（从 l l l 到 r r r）、高度（从 b b b 到 t t t）以及深度（从 f f f 到 n n n）缩放到长度为 2 2 2。

S = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] S = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} S= r−l20000t−b20000n−f200001
完整的透射投影矩阵 ：
M persp = M o r t h o P = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] M_{\text{persp}} =M_{ortho}P= \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix} Mpersp=MorthoP= r−l2n0000t−b2n00r−lr+lt−bt+b−f−nf+n−100−f−n2fn0

这里 n , f > 0 n,f>0 n,f>0， z c z_c zc 为负，近平面 z c = − n z_c=-n zc=−n，远平面 z c = − f z_c=-f zc=−f。

为了对称投影（ l = − r , b = − t l=-r, b=-t l=−r,b=−t）简化成：

M persp = [ n r 0 0 0 0 n t 0 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] M_{\text{persp}} = \begin{bmatrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix} Mpersp= rn0000tn0000−f−nf+n−100−f−n2fn0

其中 r = n ⋅ tan ⁡ ( θ h / 2 ) , t = n ⋅ tan ⁡ ( θ v / 2 ) r = n \cdot \tan(\theta_h/2),\ t = n \cdot \tan(\theta_v/2) r=n⋅tan(θh/2), t=n⋅tan(θv/2)。

变换到NDT的范围为[0,1]，3dgs中定义投影矩阵所使用的

#在3dgs中计算投影矩阵就是如此
def getProjectionMatrix(znear, zfar, fovX, fovY):
    tanHalfFovY = math.tan((fovY / 2))
    tanHalfFovX = math.tan((fovX / 2))

    top = tanHalfFovY * znear
    bottom = -top
    right = tanHalfFovX * znear
    left = -right

    P = torch.zeros(4, 4)

    z_sign = 1.0

    P[0, 0] = 2.0 * znear / (right - left)
    P[1, 1] = 2.0 * znear / (top - bottom)
    P[0, 2] = (right + left) / (right - left)
    P[1, 2] = (top + bottom) / (top - bottom)
    P[3, 2] = z_sign
    P[2, 2] = z_sign * zfar / (zfar - znear)
    P[2, 3] = -(zfar * znear) / (zfar - znear)
    return P

当 NDC（归一化设备坐标）范围为 [ 0 , 1 ] [0, 1] [0,1] （常见于 DirectX, Metal, Vulkan）且使用左手坐标系时，正交投影矩阵的形式会发生变化。

在这种情况下，我们需要将视锥体的范围映射为：

• x : [ l , r ] → [ − 1 , 1 ] x: [l, r] \to [-1, 1] x:[l,r]→[−1,1]
• y : [ b , t ] → [ − 1 , 1 ] y: [b, t] \to [-1, 1] y:[b,t]→[−1,1]
• z : [ n , f ] → [ 0 , 1 ] z: [n, f] \to [0, 1] z:[n,f]→[0,1]（注意这里 z z z 的范围和起始点）

平移矩阵 ( T T T)

平移矩阵将 x x x 和 y y y 的中心移到原点，并将 z z z 的起点线（Near 平面）移到 0。
T = [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n 0 0 0 1 ] T = \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -n \\ 0 & 0 & 0 & 1 \end{bmatrix} T= 100001000010−2r+l−2t+b−n1

缩放矩阵 ( S S S)

缩放矩阵将 x , y x, y x,y 的区间长度缩放为 2 2 2，将 z z z 的区间长度降为 1 1 1。
S = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 1 f − n 0 0 0 0 1 ] S = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{1}{f-n} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} S= r−l20000t−b20000f−n100001

---

最终的正交投影矩阵 ( M o r t h o M_{ortho} Mortho)：

将两者相乘 ( M = S ⋅ T M = S \cdot T M=S⋅T)，得到适用于 左手系且 z ∈ [ 0 , 1 ] z \in [0, 1] z∈[0,1] 的矩阵：

M o r t h o = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 1 f − n − n f − n 0 0 0 1 ] M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n} \\ 0 & 0 & 0 & 1 \end{bmatrix} Mortho= r−l20000t−b20000f−n10−r−lr+l−t−bt+b−f−nn1

左手系的正交投影矩阵与标准 OpenGL 形式（右手系, [ − 1 , 1 ] [-1, 1] [−1,1]）的主要区别：

1. Z 轴缩放系数：
   • 标准 OpenGL 是 2 f − n \frac{2}{f-n} f−n2（因为长度是 2 2 2）。
   • 此处是 1 f − n \frac{1}{f-n} f−n1（因为长度是 1 1 1）。
2. Z 轴平移项：
   • 标准 OpenGL 是 − f + n f − n -\frac{f+n}{f-n} −f−nf+n。
   • 此处是 − n f − n -\frac{n}{f-n} −f−nn。
3. 符号差异（左手系 vs 右手系）：
   • 在右手系中，相机通常看向 − z -z −z 方向，因此 z z z 的映射公式会有负号。
   • 在左手系中，相机看向 + z +z +z 方向，所以 z z z 项（ M 33 M_{33} M33）是正值 （ 1 f − n \frac{1}{f-n} f−n1）。

---

完整的透射投影矩阵为**（3dgs中的透射投影矩阵定义）**:

推导目标：

在左手系看向 +z 时，投影变换后我们希望：

• 近平面 z = n z = n z=n 映射到 NDC 的 z ndc = 0 z_{\text{ndc}} = 0 zndc=0（如果范围是[0,1]）。

• 远平面 z = f z = f z=f 映射到 NDC 的 z ndc = 1 z_{\text{ndc}} = 1 zndc=1。

• 对于 x 方向：在近平面 z = n z = n z=n 处， x = l x = l x=l 映射到 x ndc = − 1 x_{\text{ndc}} = -1 xndc=−1， x = r x = r x=r 映射到 x ndc = 1 x_{\text{ndc}} = 1 xndc=1。

• 对于 y 方向：在近平面 z = n z = n z=n 处， y = b y = b y=b 映射到 y ndc = − 1 y_{\text{ndc}} = -1 yndc=−1， y = t y = t y=t 映射到 y ndc = 1 y_{\text{ndc}} = 1 yndc=1。

M lh = [ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 f f − n − f n f − n 0 0 1 0 ] M_{\text{lh}} = \begin{bmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{f}{f-n} & -\frac{f n}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} Mlh= r−l2n0000t−b2n00−r−lr+l−t−bt+bf−nf100−f−nfn0

对称视锥简化：

若 l = − r l = -r l=−r, b = − t b = -t b=−t，则：

M lh-sym = [ n r 0 0 0 0 n t 0 0 0 0 f f − n − f n f − n 0 0 1 0 ] M_{\text{lh-sym}} = \begin{bmatrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & \frac{f}{f-n} & -\frac{f n}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} Mlh-sym= rn0000tn0000f−nf100−f−nfn0

其中 r = n ⋅ tan ⁡ ( θ h / 2 ) r = n \cdot \tan(\theta_h/2) r=n⋅tan(θh/2), t = n ⋅ tan ⁡ ( θ v / 2 ) t = n \cdot \tan(\theta_v/2) t=n⋅tan(θv/2)。

左手系（看向 +z）的透视投影矩阵与右手系（看向-z）的主要区别：

1. 第三行深度系数变为 f f − n \frac{f}{f-n} f−nf 和 − f n f − n -\frac{f n}{f-n} −f−nfn（映射到[0,1]）。

2. x 和 y 的偏移项（第三列的第一行和第二行）符号不同。

3. 第四行保持 ( 0 , 0 , 1 , 0 ) (0,0,1,0) (0,0,1,0)，将观察空间 z 存入 w 用于透视除法。

透射投影变换后NDT中的齐次坐标 ( x c , y c , z c , w c ) (x_c, y_c, z_c, w_c) (xc,yc,zc,wc)中的 w c w_c wc都要求是正值原因

无论相机坐标系是左手还是右手，最后转换到NDT坐标系都是左手坐标系，所以最后的齐次坐标 ( x c , y c , z c , w c ) (x_c, y_c, z_c, w_c) (xc,yc,zc,wc)中的 w c w_c wc都要求是正值。

主要有以下几个核心原因：

1. 透视除法的数学要求 (防止图像翻转)
   透视投影的最后一步是透视除法 ：
   x n d c = x c w c , y n d c = y c w c x_{ndc} = \frac{x_c}{w_c}, \quad y_{ndc} = \frac{y_c}{w_c} xndc=wcxc,yndc=wcyc

• 如果 w c > 0 w_c > 0 wc>0 ：物体的相对位置保持不变。原本在右边的点（ x c > 0 x_c > 0 xc>0）除以正数后仍然在右边。
• 如果 w c < 0 w_c < 0 wc<0 ：这会导致镜像翻转。原本在屏幕右侧的点会跑到左侧，原本在上方的点会跑到下方。
• 如果 w c = 0 w_c = 0 wc=0：会产生除以零的错误。这通常发生在点正好位于相机坐标系的原点（针孔位置）时。

2. 裁剪（Clipping）的需要
   在 GPU 的硬件流水线中，裁剪是在"裁剪空间"（Clip Space）进行的。裁剪的准则是：
   − w c ≤ x c ≤ w c -w_c \leq x_c \leq w_c −wc≤xc≤wc
   − w c ≤ y c ≤ w c -w_c \leq y_c \leq w_c −wc≤yc≤wc
   − w c ≤ z c ≤ w c -w_c \leq z_c \leq w_c −wc≤zc≤wc
   如果 w c w_c wc 是一个负数（比如 w c = − 5 w_c = -5 wc=−5），那么这个不等式就变成了：
   5 ≤ x c ≤ − 5 5 \leq x_c \leq -5 5≤xc≤−5
   这在数学上是不可能的（一个数不可能既大于 5 又小于 -5） 。因此，如果 w c ≤ 0 w_c \leq 0 wc≤0，GPU 会认为该点不在视锥体内，从而将其直接剔除（Cull），不进行渲染。
3. w w w 代表了"深度的物理意义"
   无论是在右手系还是左手系，投影矩阵的设计目标都是让 w c w_c wc 承载相机空间下的深度信息。

• 在右手系中 ：相机看向 − Z -Z −Z，所以物体在前方时的 z v z_v zv 是负值 。投影矩阵最后一行通常是 [ 0 , 0 , − 1 , 0 ] [0, 0, -1, 0] [0,0,−1,0]，计算得到 w c = − z v w_c = -z_v wc=−zv。因为 z v < 0 z_v < 0 zv<0，所以 w c w_c wc 变成了正值。
• 在左手系中 ：相机看向 + Z +Z +Z，物体在前方的 z v z_v zv 是正值 。投影矩阵最后一行是 [ 0 , 0 , 1 , 0 ] [0, 0, 1, 0] [0,0,1,0]，计算得到 w c = z v w_c = z_v wc=zv。所以 w c w_c wc 也是正值。

总结： w c > 0 w_c > 0 wc>0 实际上就是"物体在相机前方"的数学表达。

在渲染管线中：

• w > 0 w > 0 w>0 ：意味着点在相机前方，且能够通过裁剪测试，正确投影在屏幕上。
• w < 0 w < 0 w<0 ：意味着点在相机后方。如果不剔除，它会产生一个倒立且镜像的虚影（类似于通过针孔在相反方向形成的像），这在逻辑上是错误的。

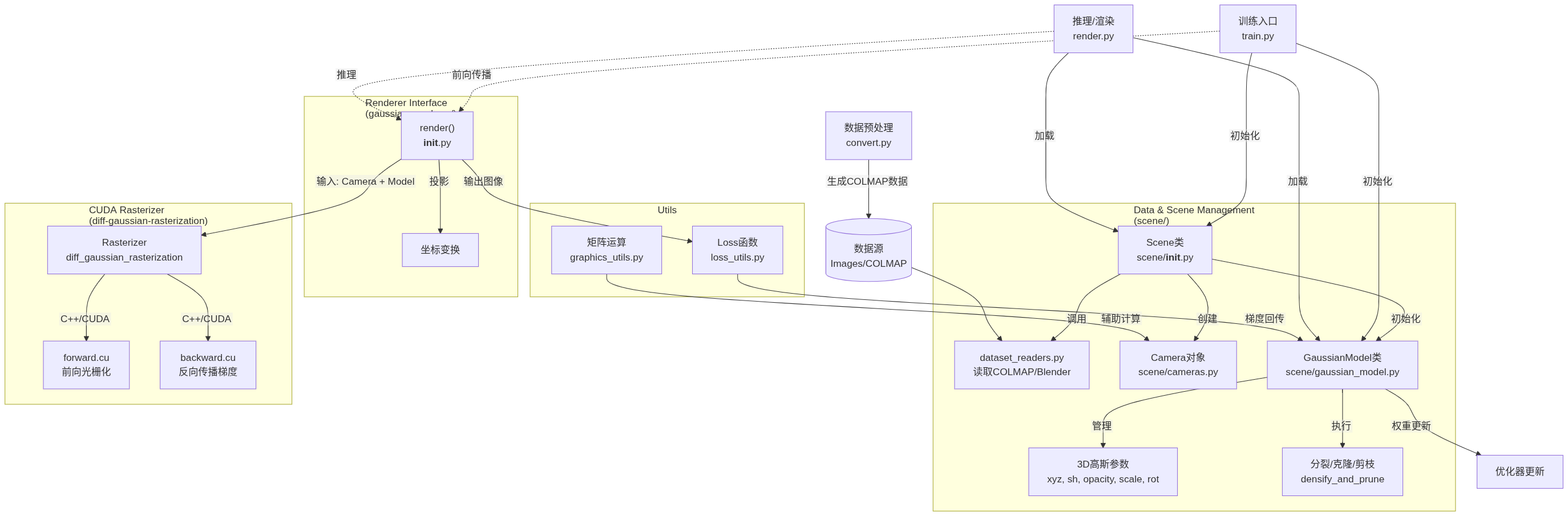
3dgs整个项目的系统流程

flowchart TD
    %% 入口脚本层
    DataPrep["数据预处理<br/>convert.py"] -->|"生成COLMAP数据"| Dataset[("数据源<br/>Images/COLMAP")]
    Train["训练入口<br/>train.py"]
    Render["推理/渲染<br/>render.py"]

    %% 场景与数据层
    subgraph SceneMgmt ["Data & Scene Management (scene/)"]
        Scene["Scene类<br/>scene/__init__.py"]
        Readers["dataset_readers.py<br/>读取COLMAP/Blender"]
        Cam["Camera对象<br/>scene/cameras.py"]
        Model["GaussianModel类<br/>scene/gaussian_model.py"]
        Param["3D高斯参数<br/>xyz, sh, opacity, scale, rot"]
        Densify["分裂/克隆/剪枝<br/>densify_and_prune"]

        Scene -->|"调用"| Readers
        Scene -->|"创建"| Cam
        Scene -->|"初始化"| Model
        Model -->|"管理"| Param
        Model -->|"执行"| Densify
    end

    Dataset --> Readers
    Train -->|"初始化"| Scene
    Train -->|"初始化"| Model
    Render -->|"加载"| Scene
    Render -->|"加载"| Model

    %% 渲染与计算层
    subgraph RendererIntf ["Renderer Interface (gaussian_renderer/)"]
        RenderFunc["render()<br/>__init__.py"]
        Projection["坐标变换"]
        RenderFunc -->|"投影"| Projection
    end

    Train -.->|"前向传播"| RenderFunc
    Render -.->|"推理"| RenderFunc

    %% 底层光栅化引擎
    subgraph CUDARaster ["CUDA Rasterizer (diff-gaussian-rasterization)"]
        Rasterizer["Rasterizer<br/>diff_gaussian_rasterization"]
        Forward["forward.cu<br/>前向光栅化"]
        Backward["backward.cu<br/>反向传播梯度"]

        Rasterizer -->|"C++/CUDA"| Forward
        Rasterizer -->|"C++/CUDA"| Backward
    end

    RenderFunc -->|"输入: Camera + Model"| Rasterizer

    %% 工具与训练循环
    subgraph Utils ["Utils"]
        Loss["Loss函数<br/>loss_utils.py"]
        Graphics["矩阵运算<br/>graphics_utils.py"]
    end

    Optimizer["优化器更新"]

    RenderFunc -->|"输出图像"| Loss
    Loss -->|"梯度回传"| Model
    Model -->|"权重更新"| Optimizer
    Graphics -->|"辅助计算"| Cam