空间相关性
多变量时间序列的数学表述
给定一个多变量时间序列集合 X={ x 1 , x 2 , ..., x C} ,其中 C 表示变量(或通道)的数量。每个变量 xi 是一个长度为 T 的观测序列 x i ={ x 1 i , x 2 i , ..., x T i} 。在任意时间步 t,系统的状态由向量 x t ∈RC 描述。
空间相关性 定义为在同一时刻 t 或存在时间滞后 τ 的情况下,变量 xi 与变量 xj 之间的统计依赖关系。如果已知 xj 的信息有助于减少对 xi 状态的不确定性,则称两者在空间上相关。
线性相关性与皮尔逊系数
最直观的空间相关性是线性的。对于两个变量序列 xj 和 xj ,其皮尔逊相关系数(Pearson Correlation Coefficient)ρi,j 定义为:
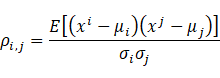
其中 μ 和 σ 分别为均值和标准差。
- 相关(Correlated ) :当
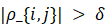 为显著性阈值,如 0.05 或 0.5时,认为变量间存在空间相关性。在深度学习模型中,这通常对应于模型倾向于通过加权求和(Weighted Sum)的方式融合这两个通道的信息。
为显著性阈值,如 0.05 或 0.5时,认为变量间存在空间相关性。在深度学习模型中,这通常对应于模型倾向于通过加权求和(Weighted Sum)的方式融合这两个通道的信息。 - 不相关(Uncorrelated ):变量间由线性无关。在正交基分解或主成分分析(PCA)中,这种不相关性意味着它们可以被映射到正交的轴上。
非线性相关性与互信息
现实世界的复杂系统(如气象动力学)往往包含高度非线性的空间相互作用。此时,基于信息论的互信息( Mutual Information, MI ) 提供了更通用的定义:
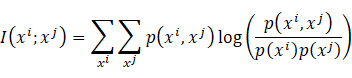
- 定义 :互信息衡量了两个变量共享的信息量。如果
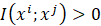 ,则意味着在空间维度上,变量 j 包含了关于变量 i 的"知识"。
,则意味着在空间维度上,变量 j 包含了关于变量 i 的"知识"。
具体的例子:
在论文《Rethinking Channel Dependence for Multivariate Time Series Forecasting》(ICLR 2024)中,研究者提出空间相关性不应局限于同时刻(Contemporaneous),而应包含时间延迟。
定义:如果存在
,使得
显著不为零,则称变量 j 是变量 i 的先行指标(Leading Indicator)。
- 相关:意味着波动首先在"上游"变量中出现,随后传播到"下游"变量。
- 不相关:不仅同时刻无关联,且在任意时间窗口内均无显著的传递效应 8。
这种定义对预测至关重要,因为预测模型的本质就是利用过去的信息推断未来。如果模型能捕捉到空间结构,就能利用 j 当前的观测值精准预测 i未来的状态。
在分析空间相关性的论文中,很少看到互信息这样的复杂指标,往往是线性相关的皮尔逊系数。
图结构与空间相关性
假设有一个时刻的数据 X(特征矩阵)和一个描述空间关系的图结构 A(邻接矩阵)。
空间相关性的提取过程可以简化为矩阵乘法:
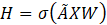
- X ( 特征):节点自己的状态(比如:每个路口的当前车速)。
- A ( 邻接矩阵) :这是空间相关性的载体。 如果节点 i 和 j 空间上相关(比如路相连),则 A ij>0,否则为 0。
- X ( 聚合) :这一步发生了"物理反应"。通过矩阵乘法,节点 i 收集了所有邻居 j 的特征。这就是 " 学习空间相关性" 的本质动作------ 信息融合。
- W ( 权重):神经网络学习的参数,决定了如何处理这些收集来的邻居信息。
具体的应用例子
例子一:交通流量预测 ( 最直观的物理空间)

- 场景:预测城市中几百个路口未来的车流量。
- 空间相关性定义 :
- 物理连接:路口 A 和 路口 B 有道路直接相连。
- 距离远近:路口 A 和 路口 B 虽然不直接相连,但直线距离很近。
- 图的构建 (A) :
- 节点:每一个传感器(路口)。
- 边:基于道路拓扑图(Road Network)。
- 权重:距离越近,影响越大。
- 学习过程:
当路口 A 发生拥堵时,GNN 会通过图结构,将"拥堵"这个特征传递给下游的路口 B。模型通过学习发现:只要 A 堵了,B 在 10 分钟后也会堵。这就是学到了空间因果性。
例子二:多变量时间序列预测 ( 隐式/ 潜在空间)
在没有明确地理位置的数据中,例如股票预测或服务器监控。

- 场景:预测几百只股票的价格,或者几百个微服务的负载。
- 空间相关性定义 :
- 行业关联:英伟达(NVIDIA)和台积电(TSMC)有供应链关系。
- 协同波动:当 A 服务负载高时,B 服务通常也会变高(可能是调用关系)。
- 图的构建 (A) :
- 方法1 (先验知识):利用行业知识图谱构建边。
- 方法2 (数据驱动 - 重点) :计算历史数据的皮尔逊相关系数 (Pearson Correlation)。如果股票 A 和 B 历史走势相似度 > 0.8,就在它们之间连一条边。
- 学习过程:
模型不仅仅看"英伟达"自己的历史走势,还会通过图聚合"台积电"和"AMD"的走势特征。如果整个"半导体板块"(邻居们)都在跌,模型会利用这个空间信息预测英伟达也会跌。
例子三:自适应/ 动态图学习 ( 由模型自己决定谁和谁相关)
这是目前最先进的方法(如 Graph WaveNet, MTGNN)。有些空间关系是人类不知道的,或者随时间变化的。
- 场景:复杂的系统监控,或者没有路网信息的交通预测。
- 图的构建 (A) :
- 不预先定义 A,而是随机初始化两个 Embedding 向量 E_1 和 E_2。
- 让模型自己学习。
- 学习过程:
模型在训练过程中,会自动寻找哪些节点之间存在依赖。它可能会发现:"虽然传感器 A 和传感器 Z 物理距离很远,但每当 A 出现异常,Z 也会异常"。模型会自动在 A 和 Z 之间生成一条"隐形的边"来传递信息。
结果:学到的 A 矩阵本身就是一种空间相关性的可视化。
注意力机制和空间相关性
1. 核心思想:维度翻转
传统 Transformer ( 关注时间)
- 输入形状:[Batch, Time_Steps, Variables]
- Token 定义:每一个时间步是一个 Token。
- Attention 作用:计算 t_1 时刻和 t_10 时刻的关系。
- 空间相关性:通常只是在 Feed Forward Network中隐式地混合变量维度,或者干脆忽略。
iTransformer ( 关注空间)
- 输入形状:[Batch, Variables, Time_Steps]
- Token 定义 :每一个变量(整个序列)是一个 Token 。
- 传感器A 过去96个点的序列 = Token 1。
- 传感器B 过去96个点的序列 = Token 2。
- Attention 作用 :计算 传感器A 和 传感器B 的关系。这就是空间相关性。
2. 具体实现:Attention 怎么算空间相关性?
假设我们有 N 个变量(Variables),时间窗口长度为 T。
步骤 1: Embedding ( 将整个序列压缩为向量)
通过一个 MLP 将每个变量的时间序列 Xi 映射到一个高维向量 Hi。
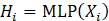
现在,我们有 N 个向量,每个向量代表一个变量的整体特征。
步骤 2: Self-Attention ( 计算空间相关性矩阵)
将这 N 个变量向量放入 Self-Attention 机制中:
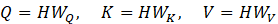
其中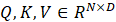 (忽略 Batch)。
(忽略 Batch)。
最关键的一步:
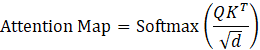
这个 Attention Map 的形状是 [N, N]。
- A_i,j 的含义:变量 i (Query) 对 变量 j(Key) 的关注程度。
- 物理意义 :如果 A_i,j很大,说明为了预测变量 i,变量 j 的历史信息非常重要。这就是模型学到的空间相关性。
步骤 3: 信息聚合
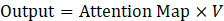
变量 i 吸收了所有与其高度相关(Attention 分数高)的其他变量的信息,更新了自己的表示。