（8-3-02）自动驾驶中的无地图环境路径探索：D* Lite路径规划系统（2）

8.3.3 实现D* Lite算法

文件d_star_lite.py实现了 D* Lite 算法的关键部分，包括计算路径、更新路径、扫描障碍物、移动并重新扫描等功能。具体来说，文件d_star_lite.py定义了计算 D* Lite 算法中路径的函数，包括计算顶部键、启发式函数、更新顶点、计算最短路径、寻找下一个最短路径、扫描障碍物、移动并重新扫描等功能。这些函数可以实现在动态环境中实时更新路径规划，并根据环境变化进行路径的调整和优化。

（1）函数topKey(queue)用于获取优先队列中最小键值的元素，它首先对队列进行排序，然后返回排序后队列中的第一个元素的前两个值作为键值。如果队列为空，则返回无穷大的键值。

def topKey(queue):
    queue.sort()
    # print(queue)
    if len(queue) > 0:
        return queue[0][:2]
    else:
        # print('empty queue!')
        return (float('inf'), float('inf'))

（2）函数heuristic_from_s(graph, id, s)用于计算启发式值，根据当前节点id和目标节点s的坐标，计算它们在x和y方向上的距离差，然后返回其中较大的值作为启发式值。

def heuristic_from_s(graph, id, s):
    x_distance = abs(int(id.split('x')[1][0]) - int(s.split('x')[1][0]))
    y_distance = abs(int(id.split('y')[1][0]) - int(s.split('y')[1][0]))
    return max(x_distance, y_distance)

（3）函数calculateKey(graph, id, s_current, k_m)用于计算D* Lite算法中的关键值，通过结合节点的g值、rhs值以及启发式函数的值，再加上一个修正因子k_m，计算出节点的关键值，并返回计算得到的关键值。

def calculateKey(graph, id, s_current, k_m):
    return (min(graph.graph[id].g, graph.graph[id].rhs) + heuristic_from_s(graph, id, s_current) + k_m, min(graph.graph[id].g, graph.graph[id].rhs))

（4）函数updateVertex(graph, queue, id, s_current, k_m)用于更新节点的信息，包括计算节点的rhs值、更新优先队列中的节点位置。首先，根据节点的子节点信息，计算出节点的rhs值；然后，将节点从优先队列中移除；最后，如果节点的rhs值与g值不相等，则重新计算节点的关键值，并将节点重新加入优先队列中。

def updateVertex(graph, queue, id, s_current, k_m):
    s_goal = graph.goal
    if id != s_goal:
        min_rhs = float('inf')
        for i in graph.graph[id].children:
            min_rhs = min(
                min_rhs, graph.graph[i].g + graph.graph[id].children[i])
        graph.graph[id].rhs = min_rhs
    id_in_queue = [item for item in queue if id in item]
    if id_in_queue != []:
        if len(id_in_queue) != 1:
            raise ValueError('more than one ' + id + ' in the queue!')
        queue.remove(id_in_queue[0])
    if graph.graph[id].rhs != graph.graph[id].g:
        heapq.heappush(queue, calculateKey(graph, id, s_current, k_m) + (id,))

（5）函数computeShortestPath(graph, queue, s_start, k_m)用于计算最短路径，并更新节点的g值。在函数中，通过检查优先队列中的最小关键值是否小于当前节点的关键值，以及当前节点的rhs值是否等于g值，来决定是否需要继续计算最短路径。在计算过程中，根据节点的g值和rhs值的关系，以及节点的子节点信息，更新节点的g值，并更新优先队列中相关节点的位置。

def computeShortestPath(graph, queue, s_start, k_m):
    while (graph.graph[s_start].rhs != graph.graph[s_start].g) or (topKey(queue) < calculateKey(graph, s_start, s_start, k_m)):
        # print(graph.graph[s_start])
        # print('topKey')
        # print(topKey(queue))
        # print('calculateKey')
        # print(calculateKey(graph, s_start, 0))
        k_old = topKey(queue)
        u = heapq.heappop(queue)[2]
        if k_old < calculateKey(graph, u, s_start, k_m):
            heapq.heappush(queue, calculateKey(graph, u, s_start, k_m) + (u,))
        elif graph.graph[u].g > graph.graph[u].rhs:
            graph.graph[u].g = graph.graph[u].rhs
            for i in graph.graph[u].parents:
                updateVertex(graph, queue, i, s_start, k_m)
        else:
            graph.graph[u].g = float('inf')
            updateVertex(graph, queue, u, s_start, k_m)
            for i in graph.graph[u].parents:
                updateVertex(graph, queue, i, s_start, k_m)
        # graph.printGValues()

（6）函数nextInShortestPath(graph, s_current)用于寻找最短路径中的下一个节点。首先检查当前节点的rhs值是否为无穷大，如果是，则打印提示信息。否则，遍历当前节点的子节点，计算子节点的代价，并找到具有最小代价的子节点作为下一个节点。若成功找到下一个节点，则返回该节点的ID，否则抛出数值错误。

def nextInShortestPath(graph, s_current):
    min_rhs = float('inf')
    s_next = None
    if graph.graph[s_current].rhs == float('inf'):
        print('You are done stuck')
    else:
        for i in graph.graph[s_current].children:
            # print(i)
            child_cost = graph.graph[i].g + graph.graph[s_current].children[i]
            # print(child_cost)
            if (child_cost) < min_rhs:
                min_rhs = child_cost
                s_next = i
        if s_next:
            return s_next
        else:
            raise ValueError('could not find child for transition!')

（7）函数scanForObstacles(graph, queue, s_current, scan_range, k_m)用于扫描当前节点周围的区域以检测障碍物。首先，根据扫描范围，初始化要更新的状态集合，并从当前节点的子节点开始更新。然后，循环迭代扫描范围，逐步扩展更新状态集合。在扫描过程中，如果发现有状态的值小于0，则表示发现了障碍物，需要进行处理，包括更新障碍物状态、更新相关节点的子节点信息，并更新优先队列中相关节点的位置。最后，返回是否发现新障碍物的标志。

def scanForObstacles(graph, queue, s_current, scan_range, k_m):
    states_to_update = {}
    range_checked = 0
    if scan_range >= 1:
        for neighbor in graph.graph[s_current].children:
            neighbor_coords = stateNameToCoords(neighbor)
            states_to_update[neighbor] = graph.cells[neighbor_coords[1]
                                                     ][neighbor_coords[0]]
        range_checked = 1
    # print(states_to_update)

    while range_checked < scan_range:
        new_set = {}
        for state in states_to_update:
            new_set[state] = states_to_update[state]
            for neighbor in graph.graph[state].children:
                if neighbor not in new_set:
                    neighbor_coords = stateNameToCoords(neighbor)
                    new_set[neighbor] = graph.cells[neighbor_coords[1]
                                                    ][neighbor_coords[0]]
        range_checked += 1
        states_to_update = new_set

    new_obstacle = False
    for state in states_to_update:
        if states_to_update[state] < 0:  # found cell with obstacle
            # print('found obstacle in ', state)
            for neighbor in graph.graph[state].children:
                # first time to observe this obstacle where one wasn't before
                if(graph.graph[state].children[neighbor] != float('inf')):
                    neighbor_coords = stateNameToCoords(state)
                    graph.cells[neighbor_coords[1]][neighbor_coords[0]] = -2
                    graph.graph[neighbor].children[state] = float('inf')
                    graph.graph[state].children[neighbor] = float('inf')
                    updateVertex(graph, queue, state, s_current, k_m)
                    new_obstacle = True
        # elif states_to_update[state] == 0: #cell without obstacle
            # for neighbor in graph.graph[state].children:
                # if(graph.graph[state].children[neighbor] != float('inf')):

    # print(graph)
    return new_obstacle

（8）函数moveAndRescan(graph, queue, s_current, scan_range, k_m)用于执行移动并重新扫描操作。首先检查当前节点是否为目标节点，如果是，则返回 'goal' 和修正因子 k_m。否则，根据当前节点获取下一个节点，并检查下一个节点是否遇到新的障碍物。如果是，则暂停移动操作，执行障碍物扫描和路径重新规划。最后，返回下一个节点的ID和修正因子 k_m。

def moveAndRescan(graph, queue, s_current, scan_range, k_m):
    if(s_current == graph.goal):
        return 'goal', k_m
    else:
        s_last = s_current
        s_new = nextInShortestPath(graph, s_current)
        new_coords = stateNameToCoords(s_new)

        if(graph.cells[new_coords[1]][new_coords[0]] == -1):  # just ran into new obstacle
            s_new = s_current  # need to hold tight and scan/replan first
        results = scanForObstacles(graph, queue, s_new, scan_range, k_m)
        # print(graph)
        k_m += heuristic_from_s(graph, s_last, s_new)
        computeShortestPath(graph, queue, s_current, k_m)
        return s_new, k_m

（9）函数initDStarLite(graph, queue, s_start, s_goal, k_m)用于初始化D* Lite算法。首先，将目标节点的rhs值设为0，并将其加入优先队列；然后，执行最短路径计算。最后，返回更新后的图、优先队列和修正因子 k_m。

def initDStarLite(graph, queue, s_start, s_goal, k_m):
    graph.graph[s_goal].rhs = 0
    heapq.heappush(queue, calculateKey(
        graph, s_goal, s_start, k_m) + (s_goal,))
    computeShortestPath(graph, queue, s_start, k_m)

    return (graph, queue, k_m)

8.3.4 路径规划可视化

文件main.py是一个基于Pygame库实现的D* Lite路径规划算法的可视化程序，创建了一个网格世界，并允许用户点击屏幕上的单元格来设置障碍物。算法将在屏幕上显示网格状态，并使用红色圆圈表示移动的机器人。当用户按下空格键时，机器人将沿最短路径移动，并根据其视野范围重新扫描环境。直到达到目标位置为止，算法将持续运行。

# 导入必要的库
# 定义颜色
BLACK = (0, 0, 0)  # 黑色
WHITE = (255, 255, 255)  # 白色
GREEN = (0, 255, 0)  # 绿色
RED = (255, 0, 0)  # 红色
GRAY1 = (145, 145, 102)  # 灰色1
GRAY2 = (77, 77, 51)  # 灰色2
BLUE = (0, 0, 80)  # 蓝色

colors = {
    0: WHITE,  # 未探索区域
    1: GREEN,  # 障碍物
    -1: GRAY1,  # 未知区域
    -2: GRAY2  # 已知障碍物
}

# 设置每个网格位置的宽度和高度
WIDTH = 40
HEIGHT = 40

# 设置每个单元格之间的间距
MARGIN = 5

# 创建一个二维数组，存储网格状态
grid = []
for row in range(10):
    grid.append([])  # 添加一个空数组，用于存储行中的单元格
    for column in range(10):
        grid[row].append(0)  # 添加一个单元格，初始状态为0

# 将第1行第5个单元格设为1（表示障碍物，行和列编号从0开始）
grid[1][5] = 1

# 初始化Pygame
pygame.init()

X_DIM = 12  # X轴维度
Y_DIM = 12  # Y轴维度
VIEWING_RANGE = 3  # 机器人的可视范围

# 设置屏幕的宽度和高度
WINDOW_SIZE = [(WIDTH + MARGIN) * X_DIM + MARGIN,
               (HEIGHT + MARGIN) * Y_DIM + MARGIN]
screen = pygame.display.set_mode(WINDOW_SIZE)

# 设置屏幕标题
pygame.display.set_caption("D* Lite路径规划")

# 退出标志
done = False

# 用于控制屏幕更新速度
clock = pygame.time.Clock()

if __name__ == "__main__":
    # 创建网格世界
    graph = GridWorld(X_DIM, Y_DIM)
    # 设置起点和终点
    s_start = 'x1y2'
    s_goal = 'x5y4'
    goal_coords = stateNameToCoords(s_goal)
    graph.setStart(s_start)
    graph.setGoal(s_goal)
    k_m = 0  # 初始化修正参数
    s_last = s_start  # 初始化上一个状态
    queue = []  # 初始化优先队列
    # 初始化D* Lite算法
    graph, queue, k_m = initDStarLite(graph, queue, s_start, s_goal, k_m)
    s_current = s_start  # 设置当前状态为起点
    pos_coords = stateNameToCoords(s_current)  # 获取当前状态坐标
    basicfont = pygame.font.SysFont('Comic Sans MS', 36)  # 设置基本字体

    # -------- 主程序循环 -----------
    while not done:
        for event in pygame.event.get():  # 用户操作
            if event.type == pygame.QUIT:  # 点击关闭按钮
                done = True  # 退出循环
            elif event.type == pygame.KEYDOWN and event.key == pygame.K_SPACE:
                # 调用移动和重新扫描函数
                s_new, k_m = moveAndRescan(
                    graph, queue, s_current, VIEWING_RANGE, k_m)
                if s_new == 'goal':
                    print('Goal Reached!')  # 达到目标点
                    done = True
                else:
                    s_current = s_new  # 更新当前状态
                    pos_coords = stateNameToCoords(s_current)  # 更新当前状态坐标
            elif event.type == pygame.MOUSEBUTTONDOWN:
                # 鼠标点击事件，设置网格状态
                pos = pygame.mouse.get_pos()
                column = pos[0] // (WIDTH + MARGIN)
                row = pos[1] // (HEIGHT + MARGIN)
                if(graph.cells[row][column] == 0):
                    graph.cells[row][column] = -1

        # 设置屏幕背景色
        screen.fill(BLACK)
        # 绘制网格
        for row in range(Y_DIM):
            for column in range(X_DIM):
                pygame.draw.rect(screen, colors[graph.cells[row][column]],
                                 [(MARGIN + WIDTH) * column + MARGIN,
                                  (MARGIN + HEIGHT) * row + MARGIN, WIDTH, HEIGHT])
                node_name = 'x' + str(column) + 'y' + str(row)
                if(graph.graph[node_name].g != float('inf')):
                    text = basicfont.render(
                        str(graph.graph[node_name].g), True, (0, 0, 200))
                    textrect = text.get_rect()
                    textrect.centerx = int(
                        column * (WIDTH + MARGIN) + WIDTH / 2) + MARGIN
                    textrect.centery = int(
                        row * (HEIGHT + MARGIN) + HEIGHT / 2) + MARGIN
                    screen.blit(text, textrect)

        # 绘制目标点
        pygame.draw.rect(screen, GREEN, [(MARGIN + WIDTH) * goal_coords[0] + MARGIN,
                                         (MARGIN + HEIGHT) * goal_coords[1] + MARGIN, WIDTH, HEIGHT])
        # 绘制移动的机器人
        robot_center = [int(pos_coords[0] * (WIDTH + MARGIN) + WIDTH / 2) +
                        MARGIN, int(pos_coords[1] * (HEIGHT + MARGIN) + HEIGHT / 2) + MARGIN]
        pygame.draw.circle(screen, RED, robot_center, int(WIDTH / 2) - 2)
        # 绘制机器人的可视范围
        pygame.draw.rect(
            screen, BLUE, [robot_center[0] - VIEWING_RANGE * (WIDTH + MARGIN), robot_center[1] - VIEWING_RANGE * (HEIGHT + MARGIN), 2 * VIEWING_RANGE * (WIDTH + MARGIN), 2 * VIEWING_RANGE * (HEIGHT + MARGIN)], 2)

        # 限制帧率为20
        clock.tick(20)
        # 更新屏幕显示
        pygame.display.flip()

    # 关闭Pygame
    pygame.quit()

运行文件main.py后显示一个可视化网格图，可以通过单击鼠标来添加或删除障碍物。按下空格键将启动D* Lite路径规划算法，每次按下空格键机器人会重新扫描环境，如图8-3所示。当机器人到达目标点时，程序将结束。

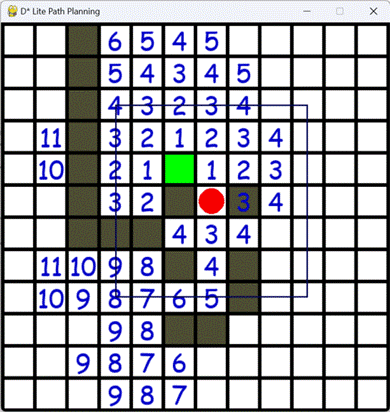
图8-3 执行效果