概念
算法
算法是求解问题的一系列计算步骤,用来将输入数据转换成输出结果
目标
正确性、可使用性、可读性、健壮性、高效率与地存储量需求
特征
有限性、确定性、可行性、输入性、输出性
与数据结构的差别
数据结构是算法设计的基础,算法是作用于数据结构之上的问题求解方法。
| 对比方面 | 数据结构 | 算法 |
|---|---|---|
| 定义 | 数据之间的逻辑关系及其存储方式 | 解决问题的一系列明确步骤和规则 |
| 研究对象 | 数据及其组织形式 | 操作数据的方法与过程 |
| 关注重点 | 数据的逻辑结构、存储结构和基本操作 | 如何在给定数据结构上高效解决实际问题 |
| 作用 | 为算法提供操作对象和实现基础 | 在数据结构基础上完成具体问题求解 |
| 与对方关系 | 是算法设计的基础 | 以数据结构作为操作对象 |
| 设计侧重点 | 选择合适的数据存储方式 | 在选定的存储结构上设计算法 |
| 表现形式 | 如数组、链表、栈、队列、树、图等 | 如排序、查找、贪心、动态规划、分治等 |
| 抽象层次 | 偏向静态的结构描述 | 偏向动态的执行过程 |
| 本质 | 逻辑基础 | 编程思想与方法 |
| 依赖关系 | 不依赖具体算法即可存在 | 必须依赖数据结构才能实现 |
算法设计的基本步骤
分析问题、选择数据结构和算法设计策略、描述算法、证明算法的正确性、算法分析
算法分析
分析算法占用计算机资源的情况
*时间复杂度
| 记号 | 名称 | 含义 |
|---|---|---|
| O(f(n)) | 大 O(上界) | 算法时间复杂度的最坏情况上界 |
| Ω(f(n)) | 大 Omega(下界) | 算法时间复杂度的最好情况或理论下界 |
| Θ(f(n)) | 大 Theta(紧确界) | 算法时间复杂度的精确阶 |
空间复杂度
临时变量所占空间
算法设计工具---STL
容器
向量、字符串、队列、链表
算法
提供了大约100个实现算法的模版函数
sort():对一个vector中的数据进行排序
迭代器
用于访问容器中的数据对象
应用
存放主数据
存放临时数据
检测数据元素的唯一性
数据排序
优先队列作为堆
递归算法
在定义一个过程或函数时出现调用本过程或本函数的成分,称之为递归。若调用自身,称之为直接递归
若过程或函数p调用过程或函数q,而q又调用p,为间接递归
应用
定义是递归的:n!
数据结构是递归的:单链表
求解问题方法是递归的
递归模型
fun(1)=1 //递归出口
fun(n)=n*fun(n-1) //递归体
每递归调用一次,就进栈一次。每递归出口或完成本次执行时,退栈一次。
分治法
对于一个规模为n的问题,可以分解成k个规模较小的问题,这些子问题相互独立且与原问题形式相同,递归地解这些小问题,然后将各个子问题的解合并得到原问题的解
解决的问题的特征
问题规模缩小到一定的程度就可以容易解决
问题可分解为若干个规模较小的相同问题
子问题的解可以合并为该问题的解
子问题相互独立,不包含公共的子问题
基本步骤
分解
求解子问题
合并
蛮力法
蛮力法是一种简单直接地解决问题的方法,通常直接基于问题的描述和所涉及的概念定义,找出所有可能的解,选择一种或多种解,不行则试探下一种可能的解
基本格式
for(x的所有可能值):{
if(x满足指定条件)
输出x;
}
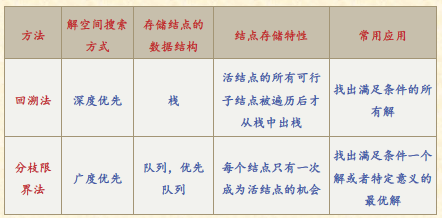
回溯法
回溯法 = 深度优先搜索 + 剪枝(尝试 + 撤销)
逐步构建解的候选,每当发现不可能得到可行解时,就"回溯"到上一步尝试其他可能性。
求解问题
找所有解、找最优解
基本步骤
确定问题的解空间树,问题的解空间树至少包含问题的一个(最优)解
确定结点的扩展搜索规则
以深度优先方式搜索解空间树,并在搜索过程中可以采用剪枝函数来避免无效搜索
剪枝函数
用约束函数在扩展结点处剪除不满足约束的子树
用限界函数剪去得不到问题解或最优解的子树
*解空间树
一个复杂问题的解决方案是由若干个小的决策步骤组成的决策序列,解决一个问题的所有可能的决策序列组成该问题的解空间
解空间中满足约束条件的决策序列称为可行解
约束条件下使目标达到最优的可行解称为最优解
所有满足约束条件的解向量组成了问题的解空间
问题的解空间一般用树形式来组织,也称为解空间树 或状态空间,树中的每一个结点确定所求解问题的一个问题状态
分枝限界法
依旧是画解空间树
找出满足约束条件的一个解或在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解
广度优先,利用限界函数选择子结点
与回溯法的区别
贪心法
在对问题的求解时总是做出当前看来是最好的选择,局部最优解
解决的问题的形状
贪心选择性质:所求问题的整体最优解可以通过一系列局部最优的选择
最优子结构性质:一个问题的最优解包含其子问题的最优解
动态规划
动态规划是一种解决多阶段决策问题的优化方法,把多阶段过程转化为一系列的单阶段问题,利用各阶段之间的关系,逐个求解