leetcode算法（104.二叉树的最大深度）

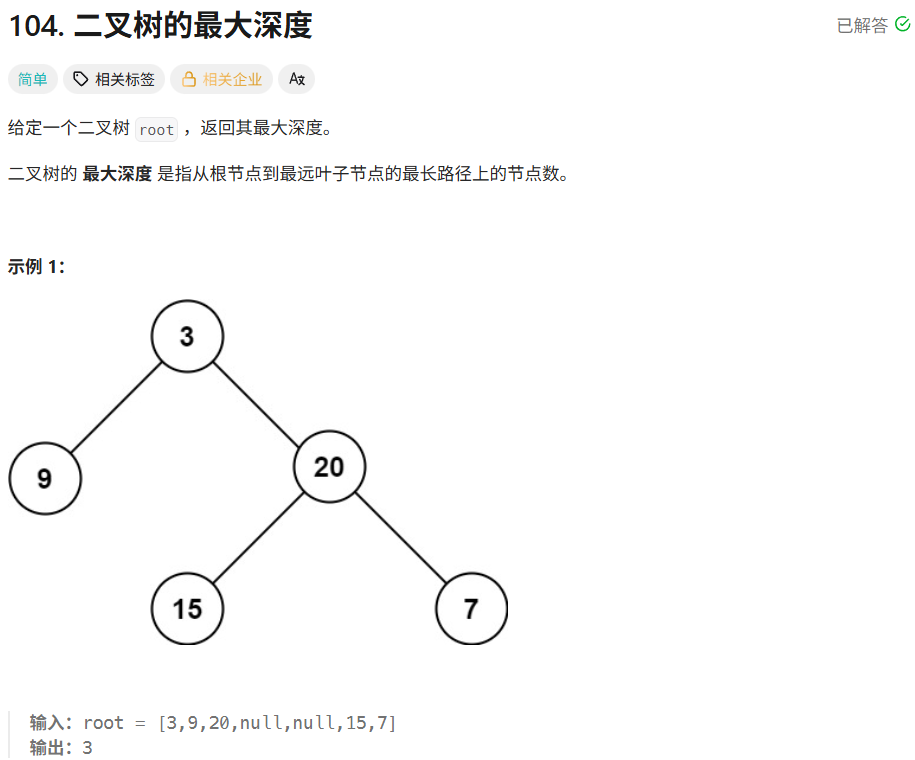
层次遍历

cpp 复制代码

class Solution {
public:
    // 计算二叉树的最大深度
    int maxDepth(TreeNode* root) {
        // 如果根节点为空，树深度为0
        if (root == NULL) return 0;
        
        // 初始化深度计数器
        int depth = 0;
        
        // 创建队列用于层序遍历
        queue<TreeNode*> que;
        // 将根节点加入队列
        que.push(root);
        
        // 当队列不为空时继续循环
        while(!que.empty()) {
            // 获取当前层的节点数量
            int size = que.size();
            
            
            // 遍历当前层的所有节点
            for (int i = 0; i < size; i++) {
                // 从队列中取出一个节点
                TreeNode* node = que.front();
                que.pop();
                
                // 如果当前节点有左子节点，将其加入队列（属于下一层）
                if (node->left) que.push(node->left);
                
                // 如果当前节点有右子节点，将其加入队列（属于下一层）
                if (node->right) que.push(node->right);
            }

           // 深度加1（处理新的一层）
            depth++; 
        }
        // 返回计算得到的最大深度
        return depth;
    }
};

二叉树递归（后序遍历）

确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

cpp 复制代码

int getdepth(TreeNode* node)

确定终止条件：如果为空节点的话，就返回0，表示高度为0。

cpp 复制代码

if (node == NULL) return 0;

确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

cpp 复制代码

int leftdepth = getdepth(node->left);       // 左
int rightdepth = getdepth(node->right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;
所以整体c++代码如下：

cpp 复制代码

class Solution {
public:
    // 递归函数，用于计算以当前节点为根的子树的最大深度
    int getdepth(TreeNode* node) {
        // 递归终止条件：如果当前节点为空，深度为0
        if (node == NULL) return 0;
        
        // 递归计算左子树的深度（后序遍历的"左"）
        int leftdepth = getdepth(node->left);
        
        // 递归计算右子树的深度（后序遍历的"右"）
        int rightdepth = getdepth(node->right);
        
        // 当前节点的深度 = 左右子树深度的最大值 + 1（+1表示当前节点本身）
        // 这是后序遍历的"中"处理逻辑
        int depth = 1 + max(leftdepth, rightdepth);
        
        // 返回当前节点的深度
        return depth;
    }
    
    // 主函数，计算二叉树的最大深度
    int maxDepth(TreeNode* root) {
        // 从根节点开始递归计算整棵树的深度
        return getdepth(root);
    }
};

说明：

递归思路：采用后序遍历（左右中）的方式，先处理左右子树，再处理当前节点
核心公式：树的深度 = max(左子树深度, 右子树深度) + 1
递归终止：空节点深度为0
时间复杂度：O(n)，需要遍历所有节点
空间复杂度：O(h)，h为树的高度，递归栈的深度

两个函数的写法？

主要是为了教学清晰性：

明确职责分离：
- maxDepth()：主接口，对外暴露
- getdepth()：内部递归实现细节
便于初学者理解

举例：

复制代码

      3      ← 深度1
     / \
    9   20    ← 深度2
       /  \
      15   7  ← 深度3

复制代码

getdepth(3)
├── getdepth(9) = 1
│   ├── getdepth(NULL) = 0
│   └── getdepth(NULL) = 0
└── getdepth(20) = 2
    ├── getdepth(15) = 1
    │   ├── getdepth(NULL) = 0
    │   └── getdepth(NULL) = 0
    └── getdepth(7) = 1
        ├── getdepth(NULL) = 0
        └── getdepth(NULL) = 0

实际上完全可以用一个函数表示 ，而且更简洁。

cpp 复制代码

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int leftdepth = maxDepth(root->left);
        int rightdepth = maxDepth(root->right);
        return max(leftdepth,rightdepth)+1;    
    }
};

在实际开发中，一个函数是更常见的写法