目的
为避免一学就会、一用就废,这里做下笔记
说明
- 本文紧承前文-线性回归,欲渐进,请循序
逻辑回归
一、是什么(定义与本质)
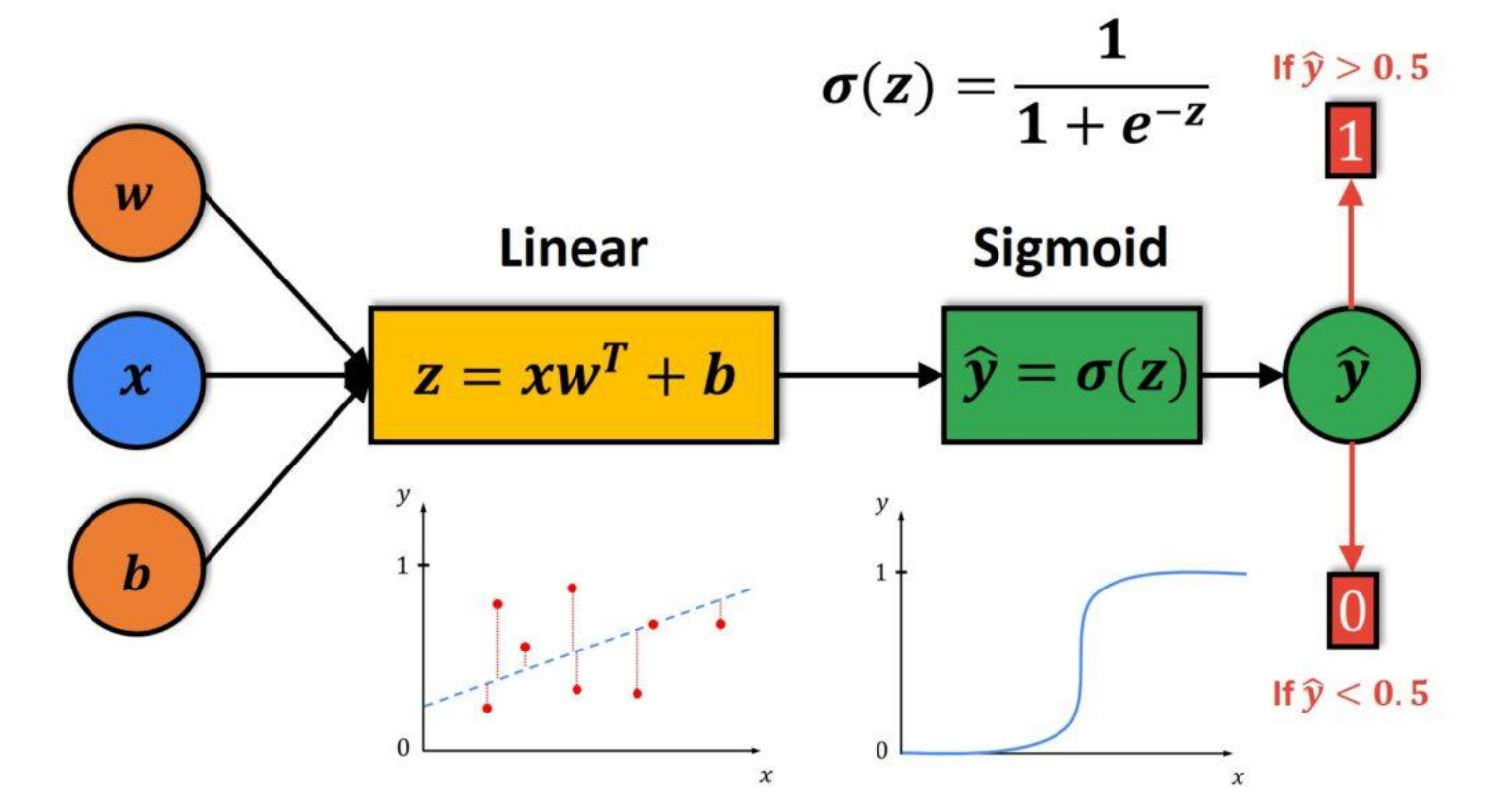
逻辑回归是一种用于解决二分类问题的统计学习方法 ,虽然名字中带有"回归",但它实际上是一种分类算法 。其核心是通过Sigmoid函数将线性回归的输出映射到(0,1)区间,解释为样本属于正类的概率。
数学本质:
- 基础形式: P ( y = 1 ∣ x ) = 1 1 + e − ( w T x + b ) P(y=1|x) = \frac{1}{1 + e^{-(w^Tx + b)}} P(y=1∣x)=1+e−(wTx+b)1
- 决策规则: P ( y = 1 ∣ x ) > 0.5 P(y=1|x) > 0.5 P(y=1∣x)>0.5 则预测为1类,否则为0类
- 决策边界: w T x + b = 0 w^Tx + b = 0 wTx+b=0(一个线性超平面)
P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x)的含义:给定输入 x x x时,输出 y = 1 y=1 y=1的概率
关键特点:
- 输出是概率值,不是硬分类
- 决策边界是线性的
- 属于广义线性模型家族
二、为什么(适用场景与优势)
为什么使用逻辑回归而不是其他方法?
适用场景:
- 二分类问题:如垃圾邮件检测、疾病诊断、客户流失预测
- 需要概率输出:不仅想知道类别,还想知道属于该类别的置信度
- 可解释性要求高:需要理解各个特征对结果的影响程度
优势:
- 计算效率高:训练和预测都很快,适合大规模数据
- 可解释性强:权重系数可直接解释为特征重要性
- 输出概率较准:输出的概率值具有实际统计意义
- 不易过拟合:特别是加上正则化后
- 数学理论成熟:有坚实的统计学基础