leetcode算法（257.二叉树的所有路径）

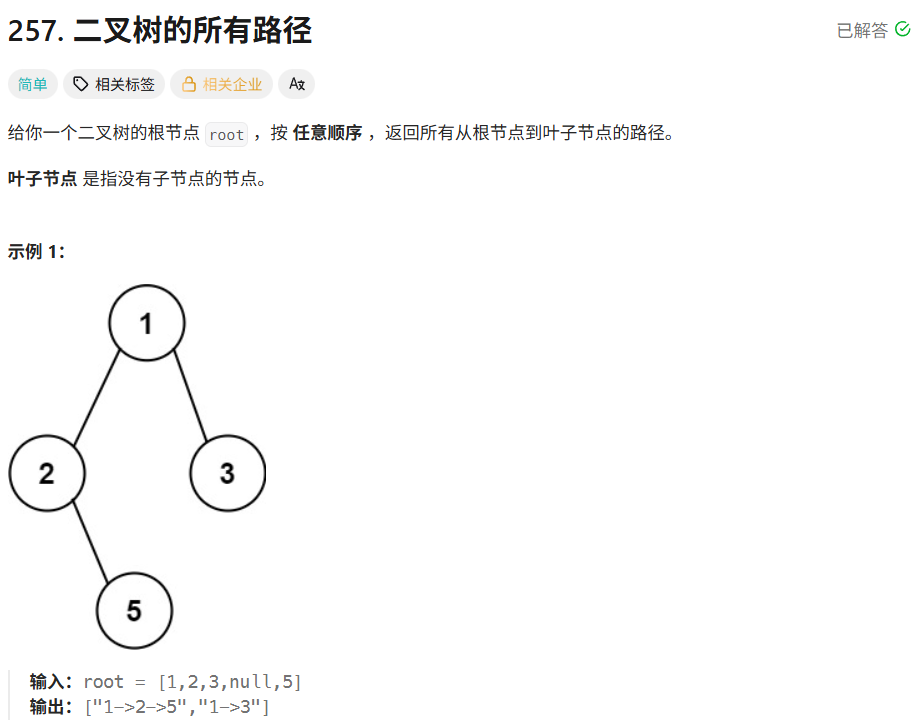
二叉树递归（前序遍历）

1.递归函数参数以及返回值

要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值，代码如下：

void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)

2.确定递归终止条件

本题要找到叶子节点。那么什么时候算是找到了叶子节点？ 是当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。

所以在本题的终止条件是：

if (cur->left == NULL && cur->right == NULL) {
    终止处理逻辑
}

使用vector<int> 结构path来记录路径，要把vector<int> 结构的path转为string格式，再把这个string 放进 result里。

终止处理逻辑如下：

if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点
    // 创建一个空字符串，用于存储最终的路径字符串
    string sPath;
    
    // 遍历path向量（存储了从根节点到当前叶子节点的所有节点值）
    // 循环到 path.size() - 1，即不包括最后一个元素
    // 因为每个元素后面需要添加"->"，但最后一个元素不需要
    for (int i = 0; i < path.size() - 1; i++) { 
        // 将第i个节点的整数值转换为字符串并追加到sPath
        sPath += to_string(path[i]);
        
        // 在节点值后面添加箭头符号"->"，表示节点间的连接
        sPath += "->";
    }
    
    // 单独处理最后一个节点（即当前叶子节点）
    // 因为最后一个节点后面不需要添加"->"
    sPath += to_string(path[path.size() - 1]); 
    
    // 将构建好的完整路径字符串添加到结果集result中
    result.push_back(sPath); 
    
    // 返回上一层递归，因为叶子节点已经处理完毕
    return;
}

解释：

1. 条件判断 ：if (cur->left == NULL && cur->right == NULL)

   • 检查当前节点是否为叶子节点（没有左右子节点）

2. 创建字符串 ：string sPath;

   • 初始化一个空字符串，用于构建最终的路径字符串

3. 循环构建路径 ：for (int i = 0; i < path.size() - 1; i++)

   • path 是一个 vector<int>，存储了从根节点到当前节点的所有节点值

   • 循环遍历除了最后一个元素之外的所有元素

   • 对每个元素：先添加节点值，再添加 "->"

4. 添加最后一个节点 ：sPath += to_string(path[path.size() - 1]);

   • 单独处理最后一个元素（叶子节点）

   • 只添加节点值，不添加 "->"

5. 保存结果 ：result.push_back(sPath);

   • 将构建好的完整路径字符串添加到结果集中

6. 返回 ：return;

   • 结束当前递归分支，返回到上一层

本题的完整代码如下：

class Solution {
private:
    // 递归遍历函数
    // cur: 当前遍历的节点
    // path: 存储当前路径的节点值（引用传递，所有递归层共享）
    // result: 存储所有完整路径的结果集（引用传递）
    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        // 先将当前节点的值添加到路径中
        // 这是"中"序遍历的一部分（前序处理）
        // 注释解释：为什么在这里添加？因为最后一个节点（叶子节点）也要加入path
        path.push_back(cur->val);
        
        // 检查当前节点是否为叶子节点（没有左右子节点）
        if (cur->left == NULL && cur->right == NULL) {
            // 如果是叶子节点，开始构建路径字符串
            string sPath; // 用于存储当前路径的字符串表示
            
            // 遍历path中除了最后一个元素之外的所有元素
            // 为每个元素添加值后加上"->"
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]); // 将整数值转换为字符串
                sPath += "->"; // 添加箭头分隔符
            }
            
            // 单独添加最后一个元素（叶子节点），后面不需要"->"
            sPath += to_string(path[path.size() - 1]);
            
            // 将构建好的完整路径字符串添加到结果集中
            result.push_back(sPath);
            
            // 返回，结束当前递归分支
            return;
        }
        
        // 如果不是叶子节点，继续遍历左子树
        if (cur->left) { // 左子树存在
            traversal(cur->left, path, result); // 递归遍历左子树
            path.pop_back(); // 回溯：移除左子树的最后一个节点值
            // 回溯的原因：返回当前节点后，需要移除刚添加的左子树节点，以便继续处理右子树
        }
        
        // 遍历右子树
        if (cur->right) { // 右子树存在
            traversal(cur->right, path, result); // 递归遍历右子树
            path.pop_back(); // 回溯：移除右子树的最后一个节点值
            // 回溯的原因：右子树处理完成后，返回上一层，需要移除当前节点值
        }
    }

public:
    // 主函数：返回二叉树所有从根节点到叶子节点的路径
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result; // 存储所有路径字符串的结果集
        vector<int> path; // 存储当前路径的节点值
        
        // 处理空树的情况
        if (root == NULL) return result;
        
        // 从根节点开始递归遍历
        traversal(root, path, result);
        
        // 返回所有路径
        return result;
    }
};

举例：

      1
     / \
    2   3
   / \
  4   5

初始调用

binaryTreePaths(根节点1)
result = []
path = []

第一次递归调用 traversal(节点1)

path.push_back(1)        // path = [1]
......
......
// 节点1不是叶子节点（有左子节点2）
// 进入左子树递归
traversal(节点2, [1], result)

第二次递归调用 traversal(节点2)

path.push_back(2)        // path = [1, 2]
......
......
// 节点2不是叶子节点（有左右子节点4和5）
// 先进入左子树递归
traversal(节点4, [1, 2], result)

第三次递归调用 traversal(节点4)

path.push_back(4)        // path = [1, 2, 4]
// 节点4是叶子节点（左右子节点都为空）
if (cur->left == NULL && cur->right == NULL) {
    // 构建路径字符串
    string sPath;
    for (int i = 0; i < 2; i++) {    // path.size()-1 = 2
        sPath += to_string(path[0]); // "1"
        sPath += "->";               // "1->"
        sPath += to_string(path[1]); // "1->2"
        sPath += "->";               // "1->2->"
    }
    sPath += to_string(path[2]);     // "1->2->4"
    result.push_back("1->2->4");     // result = ["1->2->4"]
    return;                          // 返回到节点2
}

返回到节点2，执行回溯

// 从节点4返回到节点2后
path.pop_back()          // path = [1, 2]（移除节点4）
// 节点2还有右子树，继续遍历右子树
traversal(节点5, [1, 2], result)

第四次递归调用 traversal(节点5)

path.push_back(5)        // path = [1, 2, 5]
// 节点5是叶子节点
if (cur->left == NULL && cur->right == NULL) {
    // 构建路径字符串
    string sPath;
    for (int i = 0; i < 2; i++) {    // path.size()-1 = 2
        sPath += "1->2->";
    }
    sPath += "5";                    // "1->2->5"
    result.push_back("1->2->5");     // result = ["1->2->4", "1->2->5"]
    return;                          // 返回到节点2
}

返回节点2后（关键！）

void traversal(节点2, path, result) {
    // 之前已经执行了：path.push_back(2) → path = [1, 2]
    
    // 处理左子树（已完成）
    // traversal(节点4, path, result); 已返回
    // path.pop_back(); // 这行已经执行过了，移除了节点4
    
    // 刚刚也已经处理右子树
    if (cur->right) { // cur是节点2
        traversal(节点5, path, result);  // ← 刚刚从这里返回
        path.pop_back(); // ← 回溯：移除节点5，path = [1, 2, 5] → [1, 2]
    }
    
    // 节点2的左右子树都处理完了
    // 函数结束，返回到节点1
    // 注意：这里没有对节点2执行pop_back！
}

返回节点1后

void traversal(节点1, path, result) {
    // 之前已经执行了：path.push_back(1) → path = [1]
    
    // 处理左子树
    if (cur->left) { // cur是节点1
        traversal(节点2, path, result);  // ← 刚刚从这里返回
        path.pop_back(); // ← 回溯：移除节点2，path = [1, 2] → [1]
    }
    
    // 处理右子树
    if (cur->right) {
        // 节点1还有右子树，继续遍历右子树
        // traversal(节点3, [1], result)
        traversal(节点3, path, result);
        path.pop_back(); // 移除节点3
    }
}

递归调用 traversal(节点3)

path.push_back(3)        // path = [1, 3]
// 节点3是叶子节点
if (cur->left == NULL && cur->right == NULL) {
    // 构建路径字符串
    string sPath;
    for (int i = 0; i < 1; i++) {    // path.size()-1 = 1
        sPath += "1->";
    }
    sPath += "3";                    // "1->3"
    result.push_back("1->3");        // result = ["1->2->4", "1->2->5", "1->3"]
    return;                          // 返回到节点1
}

返回到节点1，执行回溯

// 回到 traversal(节点1) 函数中：
void traversal(节点1, path, result) {
    // 之前已经执行了：path.push_back(1); → path = [1]
    
    // 左子树已处理
    if (cur->left) { // cur是节点1
        traversal(节点2, path, result); // 已完成
        path.pop_back(); // 已执行，path从[1,2]变成[1]
    }
    
    // 处理右子树
    if (cur->right) {
        traversal(节点3, path, result); // ← 刚刚从这里返回
        // 执行右子树处理完成后的回溯
        path.pop_back(); // 关键：移除节点3
        // path变化：path = [1, 3] → [1]
    }

    
执行到这里，说明：
1. 左子树已处理完毕
2. 右子树已处理完毕
3. 节点1的函数自然结束
}

如何知道左右子树均已遍历完成？

// 先处理左子树
if (cur->left) {
    traversal(cur->left, path, result);
    path.pop_back();  // 左子树处理完成后的回溯
}

// 再处理右子树
if (cur->right) {
    traversal(cur->right, path, result);
    path.pop_back();  // 右子树处理完成后的回溯
}


 当执行到这里时，说明：
 1. 左子树已处理（如果有的话）
 2. 右子树已处理（如果有的话）
 3. 函数自然结束，返回到调用者

主函数调用栈：
binaryTreePaths(根节点1)
├── traversal(节点1)
│   ├── push_back(1)                    // path = [1]
│   ├── 进入左子树: traversal(节点2)
│   │   ├── push_back(2)                // path = [1, 2]
│   │   ├── 进入左子树: traversal(节点4)
│   │   │   ├── push_back(4)            // path = [1, 2, 4]
│   │   │   ├── 发现叶子节点，记录路径
│   │   │   └── 返回（无pop_back）      // path = [1, 2, 4]
│   │   ├── pop_back() // 回溯节点4     // path = [1, 2]
│   │   ├── 进入右子树: traversal(节点5)
│   │   │   ├── push_back(5)            // path = [1, 2, 5]
│   │   │   ├── 发现叶子节点，记录路径
│   │   │   └── 返回（无pop_back）      // path = [1, 2, 5]
│   │   ├── pop_back() // 回溯节点5     // path = [1, 2]
│   │   └── 返回                        // path = [1, 2]
│   ├── pop_back() // 回溯节点2         // path = [1]
│   ├── 进入右子树: traversal(节点3)
│   │   ├── push_back(3)                // path = [1, 3]
│   │   ├── 发现叶子节点，记录路径
│   │   └── 返回（无pop_back）          // path = [1, 3]
│   ├── pop_back() // 回溯节点3         // path = [1]
│   └── 返回                            // path = [1]
└── 返回result

二叉树 迭代法

class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
         // 使用栈实现二叉树的迭代遍历（深度优先搜索）
        
        stack<TreeNode*> treeSt;   // 保存待遍历的树节点（用于DFS）
        stack<string> pathSt;      // 保存每个节点对应的完整路径字符串
        vector<string> result;     // 保存所有从根节点到叶子节点的完整路径
        
        // 处理空树的情况
        if (root == NULL) return result;
        
        // 初始化：将根节点及其路径分别压入对应的栈
        treeSt.push(root);                    // 压入根节点
        pathSt.push(to_string(root->val));    // 压入根节点的路径（只有根节点值）
        
        // 开始迭代遍历，直到所有节点都被处理
        while (!treeSt.empty()) {
            // 从栈中取出当前要处理的节点（弹出栈顶）
            TreeNode* node = treeSt.top();    // 获取栈顶节点指针
            treeSt.pop();                     // 弹出栈顶节点（移除已获取的节点）
            
            // 取出该节点对应的完整路径
            string path = pathSt.top();       // 获取栈顶路径字符串
            pathSt.pop();                     // 弹出栈顶路径（与节点同步）
            
            // 检查当前节点是否为叶子节点（没有左右子节点）
            if (node->left == NULL && node->right == NULL) {
                // 如果是叶子节点，说明已经找到一条完整路径
                result.push_back(path);       // 将完整路径添加到结果集中
                // 注意：这里不需要再往下遍历，直接进入下一次循环
                continue;                     // 实际代码中没有continue，但逻辑上不再处理子节点
            }
            
            // 先处理右子树（栈是后进先出，为了得到前序遍历的顺序）
            // 由于栈是LIFO（后进先出），为了让左子树先被处理，这里先压入右子树
            if (node->right) {                // 如果右子节点存在
                // 将右子节点压入节点栈
                treeSt.push(node->right);
                // 构建右子节点的完整路径：当前路径 + "->" + 右子节点值
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            
            // 再处理左子树
            if (node->left) {                 // 如果左子节点存在
                // 将左子节点压入节点栈
                treeSt.push(node->left);
                // 构建左子节点的完整路径：当前路径 + "->" + 左子节点值
                pathSt.push(path + "->" + to_string(node->left->val));
            }
            
            // 注意：由于栈是后进先出（LIFO），先压入右子树，后压入左子树
            // 这样左子树会先被弹出处理，符合前序遍历的顺序（中->左->右）
        }
        
        // 返回所有收集到的路径
        return result;
    }
};

容器类型	添加元素的方法	说明
vector	push_back()	在末尾添加元素
stack	push()	在栈顶添加元素
queue	push()	在队尾添加元素
deque	push_back()	在末尾添加元素

举例：
      1
     / \
    2   3
   / \
  4   5

treeSt: [] → push(1) → [1]
pathSt: [] → push("1") → ["1"]
result: []

处理节点1

TreeNode* node = treeSt.top(); // node = 1
treeSt.pop();                  // 弹出节点1，现在treeSt = []
string path = pathSt.top();    // path = "1"
pathSt.pop();                  // pathSt = []

// 节点1不是叶子节点（有左右子节点）
// 先处理右子树（节点3）
if (node->right) { // 节点3存在
    treeSt.push(node->right);          // treeSt = [3]
    pathSt.push(path + "->" + to_string(node->right->val)); 
    // pathSt = ["1->3"]
}

// 再处理左子树（节点2）
if (node->left) { // 节点2存在
    treeSt.push(node->left);           // treeSt = [3, 2]
    pathSt.push(path + "->" + to_string(node->left->val));
    // pathSt = ["1->3", "1->2"]
}

处理节点2

TreeNode* node = treeSt.top(); // 获取treeSt为[3, 2]的栈顶元素，即node = 2
treeSt.pop();                  // 弹出节点2，现在 treeSt = [3]
string path = pathSt.top();    // path = "1->2"
pathSt.pop();                  // pathSt = ["1->3"]

// 节点2不是叶子节点（有左右子节点）
// 先处理右子树（节点5）
if (node->right) { // 节点5存在
    treeSt.push(node->right);          // treeSt = [3, 5]
    pathSt.push(path + "->" + to_string(node->right->val));
    // pathSt = ["1->3", "1->2->5"]
}

// 再处理左子树（节点4）
if (node->left) { // 节点4存在
    treeSt.push(node->left);           // treeSt = [3, 5, 4]
    pathSt.push(path + "->" + to_string(node->left->val));
    // pathSt = ["1->3", "1->2->5", "1->2->4"]
}

处理节点4

TreeNode* node = treeSt.top(); // treeSt = [3, 5, 4]，取栈顶元素4，记录node = 4
treeSt.pop();                  // 弹出节点4，现在treeSt = [3, 5]
string path = pathSt.top();    // 现在pathSt = ["1->3", "1->2->5", "1->2->4"] 
                               // 记录栈顶path = "1->2->4"
pathSt.pop();                  // 弹出栈顶，现在pathSt = ["1->3", "1->2->5"]

// 节点4是叶子节点
if (node->left == NULL && node->right == NULL) {
    result.push_back(path);    // result = ["1->2->4"]
    continue;

有 continue;
叶子节点：执行 result.push_back(path); 后，立即跳过剩余代码
不会检查 if (node->right) 和 if (node->left),直接进行下一次while循环

}

// 节点4没有子节点，不压入新节点

处理节点5

TreeNode* node = treeSt.top(); // node = 5
treeSt.pop();                  // treeSt = [3]
string path = pathSt.top();    // path = "1->2->5"
pathSt.pop();                  // pathSt = ["1->3"]

// 节点5是叶子节点
if (node->left == NULL && node->right == NULL) {
    result.push_back(path);    // result = ["1->2->4", "1->2->5"]
}

// 节点5没有子节点，不压入新节点

处理节点3

TreeNode* node = treeSt.top(); // node = 3
treeSt.pop();                  // treeSt = []
string path = pathSt.top();    // path = "1->3"
pathSt.pop();                  // pathSt = []

// 节点3是叶子节点
if (node->left == NULL && node->right == NULL) {
    result.push_back(path);    // result = ["1->2->4", "1->2->5", "1->3"]
}

// 节点3没有子节点，不压入新节点

循环结束

while (!treeSt.empty()) // treeSt为空，退出循环
return result;  // 返回 ["1->2->4", "1->2->5", "1->3"]

先压入：右子树 → 左子树
弹出时：左子树（后进先出）→ 右子树
这样就实现了前序遍历的顺序：根 → 左 → 右