前言
其实 DP 优化这一块还是一个非常大的部分,知识点很多,大大小小的方法也有一大堆。我本来不是很想写,不过知识点还是很多,不得不整理一下。
正文
在讲单调队列优化 DP 之前,我们还需要了解一下什么是单调队列。
什么是单调队列
单调队列,是一种常见的动态求区间最大或最小值的方法,它可以把时间复杂度降一个幂次。
单调队列相对于线段树的优点主要是一个:时空都比线段树小。这也是它至今没有被线段树所替代的原因。
怎么实现单调队列
既然叫做单调队列,那肯定要满足单调。也正是因为它单调,我们才能精准的找出最大值和最小值。
为了方便讲解,我们选择一道例题(选自洛谷):
P1886 【模板】单调队列 / 滑动窗口
题目描述
有一个长为 nnn 的序列 aaa,以及一个大小为 kkk 的窗口。现在这个窗口从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最小值和最大值。
例如,对于序列 [1,3,−1,−3,5,3,6,7][1,3,-1,-3,5,3,6,7][1,3,−1,−3,5,3,6,7] 以及 k=3k = 3k=3,有如下过程:
窗口位置最小值最大值[1 3 -1] -3 5 3 6 7 −13 1 [3 -1 -3] 5 3 6 7 −33 1 3 [-1 -3 5] 3 6 7 −35 1 3 -1 [-3 5 3] 6 7 −35 1 3 -1 -3 [5 3 6] 7 36 1 3 -1 -3 5 [3 6 7]37\def\arraystretch{1.2} \begin{array}{|c|c|c|}\hline \textsf{窗口位置} & \textsf{最小值} & \textsf{最大值} \\ \hline \verb![1 3 -1] -3 5 3 6 7 ! & -1 & 3 \\ \hline \verb! 1 [3 -1 -3] 5 3 6 7 ! & -3 & 3 \\ \hline \verb! 1 3 [-1 -3 5] 3 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 [-3 5 3] 6 7 ! & -3 & 5 \\ \hline \verb! 1 3 -1 -3 [5 3 6] 7 ! & 3 & 6 \\ \hline \verb! 1 3 -1 -3 5 [3 6 7]! & 3 & 7 \\ \hline \end{array} 窗口位置[1 3 -1] -3 5 3 6 7 1 [3 -1 -3] 5 3 6 7 1 3 [-1 -3 5] 3 6 7 1 3 -1 [-3 5 3] 6 7 1 3 -1 -3 [5 3 6] 7 1 3 -1 -3 5 [3 6 7]最小值−1−3−3−333最大值335567输入格式
输入一共有两行,第一行有两个正整数 n,kn,kn,k;
第二行有 nnn 个整数,表示序列 aaa。
输出格式
输出共两行,第一行为每次窗口滑动的最小值;
第二行为每次窗口滑动的最大值。
输入输出样例 #1
输入 #1
8 3 1 3 -1 -3 5 3 6 7输出 #1
-1 -3 -3 -3 3 3 3 3 5 5 6 7说明/提示
【数据范围】
对于 50%50\%50% 的数据,1≤n≤1051 \le n \le 10^51≤n≤105;
对于 100%100\%100% 的数据,1≤k≤n≤1061\le k \le n \le 10^61≤k≤n≤106,ai∈[−231,231)a_i \in [-2^{31},2^{31})ai∈[−231,231)。
这是一道很经典的单调队列问题。通过这道例题我将详细讲解单调队列的使用方法与适用范围。
首先我们考虑朴素做法:枚举这个窗口的最后一位,枚举窗口内的每一个数,求出最大(小)值。时间复杂度 O(nk)O(nk)O(nk),明显过不了。
现在考虑优化:假设我们现在要求最大值,还是枚举窗口的最后一位 iii。
当 i=1i=1i=1 时,a1=1a_1=1a1=1,直接把 111 放入队列,此时队列为 [1][1][1]。
当 i=2i=2i=2 时,a2=3a_2=3a2=3,因为 a2>a1a_2>a_1a2>a1,所以把 111 弹出队列尾部,把 222 放入队列尾部,此时队列为 [2][2][2]
当 i=3i=3i=3 时,a3=−1a_3=-1a3=−1,因为 a3<a1a_3\lt a_1a3<a1,所以把 333 放入队列尾部,此时队列为 [3,2][3,2][3,2]。此时的最大值就是 a2=3a_2=3a2=3。
当 i=4i=4i=4 时,a4=−3a_4=-3a4=−3,因为 a4<a3a_4\lt a_3a4<a3,所以把 444 放入队列尾部,此时队列为 [4,3,2][4,3,2][4,3,2]。此时的最大值为 a2=3a_2=3a2=3。
当 i=5i=5i=5 时,a5=5a_5=5a5=5,因为 5−3≥25-3\ge25−3≥2,所以把 222 从队首弹出,因为 a5>a4a_5\gt a_4a5>a4,所以把 444 从队列尾部弹出,因为 a5>a3a_5\gt a_3a5>a3,所以把 333 从队列尾部弹出,此时队列为空,所以直接把 555 放入队首,此时队列为 [5][5][5],因此最大值为 a5=5a_5=5a5=5。
当 i=6i=6i=6 时,a6=3a_6=3a6=3,因为 a6<a5a_6\lt a_5a6<a5,所以把 666 推入队尾,此时队列为 [6,5][6,5][6,5],所以最大值为 a5=5a_5=5a5=5。
当 i=7i=7i=7 时,a7=6a_7=6a7=6,因为 a7>a6a_7\gt a_6a7>a6,所以把 666 从队尾弹出,因为 a7>a5a_7\gt a_5a7>a5,所以把 555 从队尾弹出,此时队列为空,所以直接把 777 推入队首,此时队列为 [7][7][7],所以最大值为 a7=6a_7=6a7=6。
当 i=8i=8i=8 时,a8=7a_8=7a8=7,因为 a8>a7a_8\gt a_7a8>a7,所以把 777 从队尾弹出,此时队列为空,所以直接把 888 推入队首,此时队列为 [8][8][8],所以最大值为 a8=7a_8=7a8=7。
所以最终答案为 3,3,5,5,6,73,3,5,5,6,73,3,5,5,6,7,跟答案一模一样。
通过上面模拟的过程,我们其实可以初步写出单调队列的代码:
cpp
deque<int>dq;
for(int i=1;i<=n;i++)
{
while(!dq.empty()&&a[dq.back()]<a[i])
{
dq.pop_back();
}
dq.push_back(i);
while(dq.front()<=i-k)
{
dq.pop_front();
}
if(i>=k)
{
cout<<a[dq.front()]<<" ";
}
}但是这样也只是看到了表象,我们要了解单调队列深层的原理。
因为我们要求最大值,所以我们肯定会想办法把最大值放在最前面。所以单调队列整体要么是单调递增(求最大值),要么是单调递减(求最小值),这样最值就会被放在最前面。
现在我们要求最大值,所以单调队列是单调递增的(不是指单调队列里面的值,而是单调队列里面的数所对应的值,因为我们保存的是下标),假设我要放进去一个数,那我们不可能上来就把这个数放在队首,不然不一定单调。肯定是先从最尾部开始比较。
那如果我比队列尾部的数小,直接放进去就能满足单调性。可如果我比队列尾部的数大,这时就要思考为什么我们会直接把尾部弹出:因为放在单调队列里面的数必定都是在你前面,在你后面的数如果要取最大值,肯定会优先考虑当前这个数,而不是比它小的数,再加上单调队列里面的数都在你前面,能延伸到的范围没你远,所以这些数其实在这一刻就已经没用了,所以直接弹出。
如果没看懂上面所写的可以看看下面这张图:
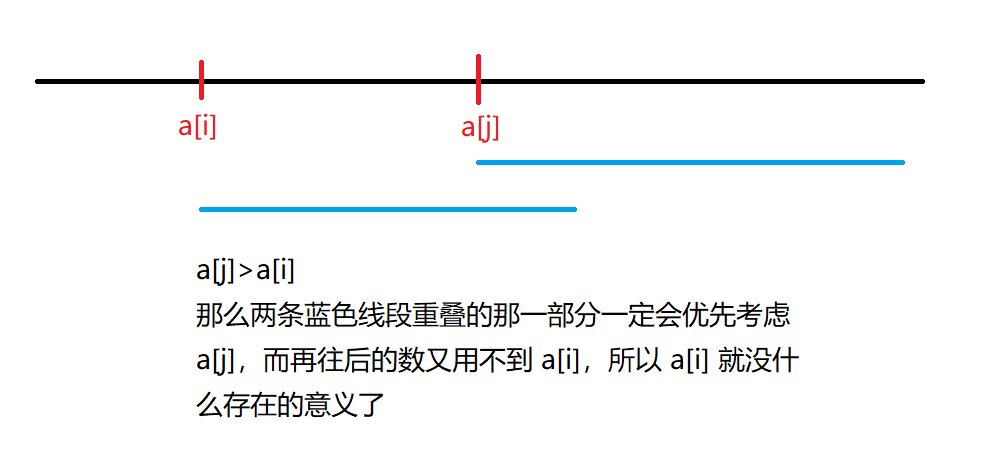
现在要取最大值,因为有一个范围限制,所以如果我当前的最大值在这个范围之外,那么直接把最大值扔掉就好(这个比上面的要好想的多),继续考虑下一个。这也是为什么队列要保持单调,不然在删除最大值的时候就不好办了。
相应的,求最小值这个问题就很简单了。在此不展示代码。
单调队列优化 DP
了解了单调队列,现在我们来看看单调队列是如果优化 DP 的。
因为单调队列的特性,使得它的时间复杂度接近于 O(1)O(1)O(1),在求动态区间最值这一块与显著的优化效果。一般优化的都是形如 fi=minj=lr{fj+F(j)+C}f_i=\min_{j=l}^r\{f_j+F(j)+C\}fi=minj=lr{fj+F(j)+C} 的转移方程,其中 CCC 时常数,F(j)F(j)F(j) 表示以 jjj 为自变量的一个函数,这个 jjj 的确定方式一般是看 DP 的哪一维在变,r−lr-lr−l 一般情况下是一个定值,或者是 [l,r][l,r][l,r] 这个区间在不断往一边走,不会出现突然换方向的这种情。
我们还是用一道例题来讲解(选自洛谷):
P10978 Fence
题目描述
一组由 kkk(1≤k≤1001 \leq k \leq 1001≤k≤100) 名工人组成的团队需要粉刷一堵包含 NNN 个木板的围栏,这些木板从左到右编号为 111 到 NNN(1≤N≤16,0001 \leq N \leq 16,0001≤N≤16,000)。每个工人 iii(1≤i≤k1 \leq i \leq k1≤i≤k)应该坐在木板 SiS_iSi 前,他只能粉刷一个连续的区间(这意味着区间内的木板应该是连续的)。这个区间必须包含木板 SiS_iSi(特别地,这个区间也可以为空,即一个工人可以不工作 )。此外,每个工人粉刷的木板数量不能超过 LiL_iLi 个,并且每粉刷一个木板他会得到 PiP_iPi 美元(1≤Pi≤10,0001 \leq P_i \leq 10,0001≤Pi≤10,000)。每个木板最多只能由一个工人粉刷。所有的 SiS_iSi 都是不同的。
作为团队的领导者,你需要为每个工人确定他们应该粉刷的区间,并且确保总收入最大化。总收入代表工人个人收入的总和。
编写一个程序来确定 kkk 名工人获得的总最大收入。
输入格式
输入的第一行是是两个正整数 N,kN,kN,k。
接下来 kkk 行,每行三个正整数 Li,Pi,SiL_i,P_i,S_iLi,Pi,Si。
输出格式
输出一个整数,表示总最大收入。
输入输出样例 #1
输入 #1
8 4 3 2 2 3 2 3 3 3 5 1 1 7输出 #1
17
(因为作者最近只做了蓝及以上的单调队列优化题,暂时找不到别的,所以只能用这道题了)。
首先我们很容易想到设 fi,jf_{i,j}fi,j 表示前 iii 个工人,最后一块刷的木板是 jjj 时的最大代价。然后可以非常轻松的写出状态转移方程:
fi,j=maxk=1Li{fi−1,j−k+Pi×k}f_{i,j}=\max_{k=1}^{L_i}\{f_{i-1,j-k}+P_i\times k\}fi,j=k=1maxLi{fi−1,j−k+Pi×k}
明显过不去,不过因为这题数据很水,也是可以直接飞过去的。
给一下暴力代码:
cpp
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);//如果这个工人不干活
if(j>=a[i].s)
{
for(int k=1;k<=a[i].l;k++)
{
if(j-k>=0&&j-k<a[i].s)
{
f[i][j]=max(f[i][j],f[i-1][j-k]+k*a[i].p);
}
}
}
}
}现在考虑优化:按照我们上面写的,单调队列优化的使用条件应该是里面是求 fjf_jfj 与和 jjj 有关的一个函数的和。这里因为在循环 jjj 时 iii 不变,所以这里变化的是 j−kj-kj−k,也就是说:我们要把那个 max 里面的东西换成 fi−1,j−k+F(j−k)+Cf_{i-1,j-k}+F(j-k)+Cfi−1,j−k+F(j−k)+C 的形式,但是我们能得到的只有 f[i-1][j-k]+k*a[i].p,所以我们可以把后面的 k*a[i].p 拆开,变成 j*a[i].p-(j-k)*a[i].p,于是方程就变成了这样:
fi,j=max{fi−1,j−k−(j−k)×pi+j×pi}f_{i,j}=\max\{f_{i-1,j-k}-(j-k)\times p_i+j\times p_i\}fi,j=max{fi−1,j−k−(j−k)×pi+j×pi}
这时我们就会发现:这个状态转移方程变成了我们熟知的单调队列优化的形式。
因此我们考虑一个新的值 l=j−kl=j-kl=j−k,枚举 lll 可以得到 fi−1,l−l×pif_{i-1,l}-l\times p_ifi−1,l−l×pi,这个东西可以用单调队列优化,这个 lll 的范围还是很好算的,这里就不带着算了。
因此我们就可以用单调队列把时间复杂度优化到 O(nm)O(nm)O(nm)。显然能过。
放一下核心代码:
cpp
for(int i=1;i<=m;i++)
{
dq.clear();
for(int j=max(0ll,a[i].s-a[i].l);j<a[i].s;j++)//这里其实就是枚举 l,把这些数提前放进单调队列
{
while(!dq.empty()&&f[i-1][dq.front()]-dq.front()*a[i].p<f[i-1][j]-j*a[i].p)
{
dq.pop_front();
}
dq.push_front(j);
}
for(int j=1;j<=n;j++)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(j>=a[i].s)
{
while(!dq.empty()&&dq.back()<j-a[i].l)//当前这个 l 的最小为 j-a[i].l
{
dq.pop_back();
}
if(!dq.empty())
{
f[i][j]=max(f[i-1][dq.back()]-dq.back()*a[i].p+j*a[i].p,f[i][j]);
}
}
}
}上面那份代码是把尾部作为最大的,倒过来用头也可以。
什么时候用单调队列优化
这是一个很好的问题。在讲这个问题之前,我们需要再看一道例题:
P4644 [USACO05DEC] Cleaning Shifts S
题目描述
约翰的奶牛们从小娇生惯养,她们无法容忍牛棚里的任何脏东西。约翰发现,如果要使这群有洁癖的奶牛满意,他不得不雇佣她们中的一些来清扫牛棚,约翰的奶牛中有 N(1≤N≤10000)N(1 \leq N \leq 10000)N(1≤N≤10000) 头愿意通过清扫牛棚来挣一些零花钱。
由于在某个时段中奶牛们会在牛棚里随时随地地乱扔垃圾,自然地,她们要求在这段时间里,无论什么时候至少要有一头奶牛正在打扫。需要打扫的时段从某一天的第 MMM 秒开始,到第 EEE 秒结束 (0≤M≤E≤86399)(0 \leq M \leq E \leq 86399)(0≤M≤E≤86399)。注意这里的秒是指时间段而不是时间点,也就是说,每天需要打扫的总时间是 E−M+1E-M+1E−M+1 秒。
约翰已经从每头牛那里得到了她们愿意接受的工作计划:对于某一头牛,她每天都愿意在笫 T1...T2T_1 \ldots T_2T1...T2 秒的时间段内工作 (M≤T1≤T2≤E)(M \leq T_1 \leq T_2 \leq E)(M≤T1≤T2≤E) ,所要求的报酬是 SSS 美元 (0≤S≤500000)(0 \leq S \leq 500000)(0≤S≤500000)。与需打扫时段的描述一样,如果一头奶牛愿意工作的时段是每天的第 10...2010 \ldots 2010...20 秒,那她总共工作的时间是 111111 秒,而不是 101010 秒。
约翰一旦决定雇佣某一头奶牛,就必须付给她全额的工资,而不能只让她工作一段时间,然后再按这段时间在她愿意工作的总时间中所占的百分比来决定她的工资。现在请你帮约翰决定该雇佣哪些奶牛以保持牛棚的清洁,当然,在能让奶牛们满意的前提下,约翰希望使总花费尽量小。
输入格式
第 111 行: 333 个正整数 N,M,EN,M,EN,M,E 。
第 222 到 N+1N+1N+1 行:第 i+1i+1i+1 行给出了编号为 iii 的奶牛的工作计划,即 333 个正整数 T1,T2,ST_1,T_2,ST1,T2,S 。
输出格式
输出一个整数,表示约翰需要为牛棚清理工作支付的最少费用。如果清理工作不可能完成,那么输出 −1-1−1 。
输入输出样例 #1
输入 #1
3 0 4 0 2 3 3 4 2 0 0 1输出 #1
5说明/提示
约翰有 333 头牛,牛棚在第 000 秒到第 444 秒之间需要打扫。 约翰雇佣前两头牛清扫牛棚,可以只花 555 美元就完成一整天的清扫。
这题有一种方法用最短路做,不过这里我们要讲 DP,所以不细谈。
我们可以设 fif_ifi 表示包含时间点 iii 所需要的费用。那么可以得到方程:
fedi=minj=sti−1edi{fj+si}f_{ed_i}=\min_{j=st_i-1}^{ed_i}\{f_j+s_i\}fedi=j=sti−1minedi{fj+si}
我们会发现:这里又有求最值的操作。可是这里我们并不能用单调队列优化。为什么呢?因为我们每次循环的范围 [sti−1,edi][st_i-1,ed_i][sti−1,edi] 并不是一直往一个方向走的。也就是说,我们每次的枚举范围不是像这个样子的:

所以,如果我要求包括前面部分的最小值,那么用单调队列就没法返回去算前面的值(因为我们的队列把一个数弹出之后就没法再弹入了)。所以不能用单调队列。而这道题真正的优化方法是我们后面要讲的数据结构优化 DP。
总结一下:单调队列优化 DP 的使用情况是:
- 多次求最值。
- 每次求最值的区间范围一定只朝着一个方向移动。