【微分方程——传染病模型（一）】

3Bronze1Pyramid2026-01-16 17:02

一、前言

  • 传染病（如SARS、艾滋病、新冠肺炎等）严重威胁着人类健康与社会稳定。 历史上多次疫情爆发，特别是2020年新冠肺炎的突袭，凸显了掌握传染病传播规律、预测感染规模及制定防控策略的紧迫性。尽管各类疾病的病理与传播途径各异，但数学模型已成为研究其传播过程、分析传播特征的重要工具

  • 建立传染病数学模型，旨在从理论上描述疾病的演化规律，为预防爆发、控制蔓延及消除疾病提供科学的信息支持。常见的传染病模型按照传染病类型分为 SI、SIR、SIRS、SEIR 模型等，按照传播机理又分为基于常微分方程、偏微分方程、网络动力学的不同类型。本文将避开复杂的病理学细节，仅从一般传播机理出发，构建并探讨几种最常用的传染病模型，以期为公共卫生决策提供定量化的参考依据

二、传染病模型中通用的符号系统

(1) 易感者（S，Susceptible）：潜在的可感染人群；

(2) 潜伏者（E，Exposed）：已被传染但没表现出来的人群；

(3) 感染者（I，Infected）：确诊感染的人；

(4) 康复者（R，Recovered）：已痊愈的感染者，体内含抗体

三、SI 模型介绍

3.1 模型定义与变量

SI模型是最基本的传染病模型，将人群划分为两大类：

  • S (Susceptible)：易感染者，即健康人。这部分人未得病，但缺乏免疫力，与患者接触后容易被感染；
  • I (Infective)：已感染者，即患者。这部分人已得病，并具有将疾病传染给易感染者的能力

3.2 基本假设

为了简化数学推导，模型设定以下前提：

  • 人口恒定：不考虑人口的迁移（迁入/迁出）以及自然的出生和死亡；
  • 总量守恒：设总人数为 ( N )，则在任意时刻 ( t )，总人数满足：
    N=S(t)+I(t)N = S(t) + I(t)N=S(t)+I(t)

3.3 传播机理

  • 参数设定：设 β\betaβ 为单位时间内，易感染者与已感染者接触且被传染的强度；
  • 转化逻辑：单位时间内，由易感染者 S 转换为已感染者 I 的人数计算公式为：
    新增感染人数=β×SN×IN×N=βSIN新增感染人数 = \beta \times \frac{S}{N} \times \frac{I}{N} \times N = \beta \frac{SI}{N}新增感染人数=β×NS×NI×N=βNSI
    注：SN\frac{S}{N}NS 和 IN\frac{I}{N}NI分别代表易感染者、已感染者在人群中的比例
第一步：建立差分方程

考虑极短时间间隔 Δt\Delta tΔt：

  • 易感染者 S 的变化：人数减少（转变为 ( I )），变化量为负：
    S(t+Δt)−S(t)=−βS(t)⋅I(t)NΔtS(t + \Delta t) - S(t) = -\beta \frac{S(t) \cdot I(t)}{N} \Delta tS(t+Δt)−S(t)=−βNS(t)⋅I(t)Δt
  • 已感染者 I 的变化：人数增加（来源于 ( S )），变化量为正：
    I(t+Δt)−I(t)=βS(t)⋅I(t)NΔtI(t + \Delta t) - I(t) = \beta \frac{S(t) \cdot I(t)}{N} \Delta tI(t+Δt)−I(t)=βNS(t)⋅I(t)Δt
第二步：转化为微分方程

利用导数的定义（令 Δt\Delta tΔt ------> 0 ）：

  • 易感染者 S 的变化率：
    dSdt=lim⁡Δt→0S(t+Δt)−S(t)Δt=−βS⋅IN\frac{dS}{dt} = \lim_{\Delta t \to 0} \frac{S(t + \Delta t) - S(t)}{\Delta t} = -\beta \frac{S \cdot I}{N}dtdS=Δt→0limΔtS(t+Δt)−S(t)=−βNS⋅I
  • 已感染者 I 的变化率：
    dIdt=lim⁡Δt→0I(t+Δt)−I(t)Δt=βS⋅IN\frac{dI}{dt} = \lim_{\Delta t \to 0} \frac{I(t + \Delta t) - I(t)}{\Delta t} = \beta \frac{S \cdot I}{N}dtdI=Δt→0limΔtI(t+Δt)−I(t)=βNS⋅I

📌状态转移图：

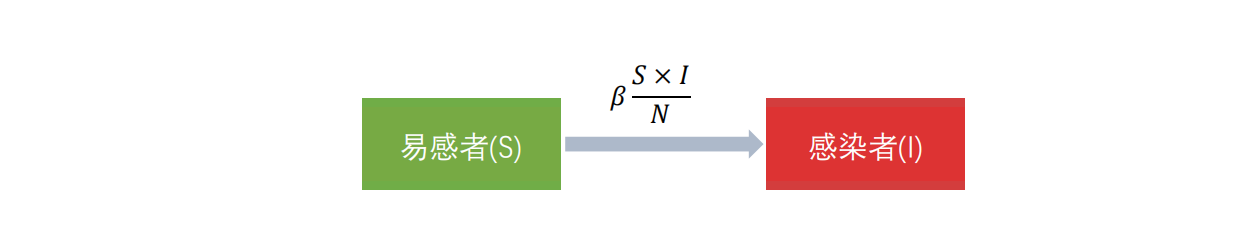
SI模型的动力学微分方程组为：
{dSdt=−βSINdIdt=βSIN\begin{cases} \frac{dS}{dt} = -\beta \frac{SI}{N} \\ \frac{dI}{dt} = \beta \frac{SI}{N} \end{cases}{dtdS=−βNSIdtdI=βNSI

c

matlab 复制代码 
clc;clear
global TOTAL_N   % 定义总人数为全局变量（可以在子函数中使用）
TOTAL_N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun1',[1:200],[TOTAL_N-i0 i0]); 
x = round(x);  % 可以对x进行四舍五入(人数为整数)
% % 注意：四舍五入后人口数加起来可能不等于总人数了，但这个误差可以忽略。
figure(1)
 % x的第一列是易感染者S的数量，x的第二列是患者I的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-','Linewidth',1.5)  % 线的宽度设置为1.5
legend('易感染者S','患者I')
matlab 复制代码 
function dx=fun1(t,x)   % 大家可以修改里面的参数，来看结果的变化
    global TOTAL_N   % 定义总人数为全局变量
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    dx = zeros(2,1);  % x(1)表示S  x(2)表示I
    dx(1) = - beta*x(1)*x(2)/TOTAL_N;  
    dx(2) = beta*x(1)*x(2)/TOTAL_N;
end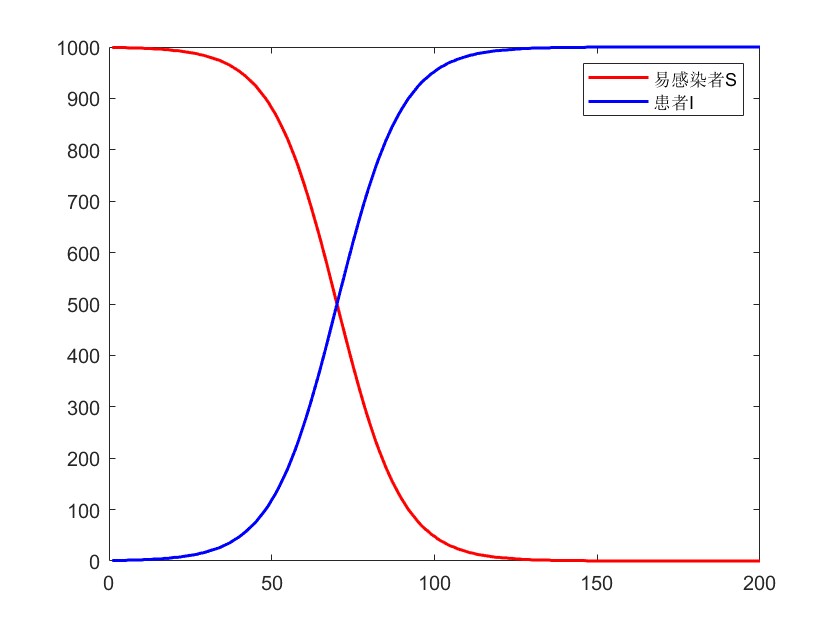

📌3.5 SI 模型拓展

疾病流行期间，人口出生率和自然死亡率分别为μ\muμ和 vvv ，因病的死亡率为ddd，其状态转移图形为：

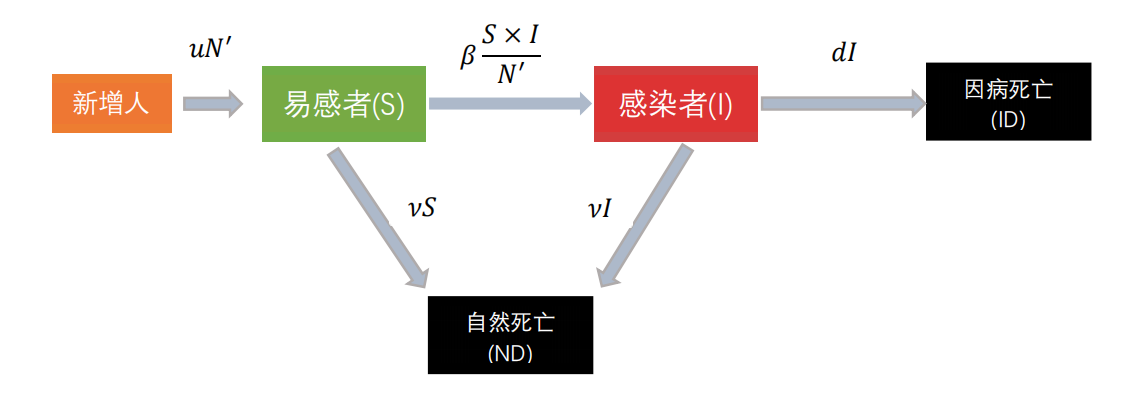
对应的微分方程组为：
{dSdt=−βS×IN′+uN′−vSdIdt=βS×IN′−dI−vIdIDdt=dIdNDdt=vS+vI \begin{cases} \frac{dS}{dt} = -\beta \frac{S \times I}{N'} + uN' - vS \\ \frac{dI}{dt} = \beta \frac{S \times I}{N'} - dI - vI \\ \frac{dID}{dt} = dI \\ \frac{dND}{dt} = vS + vI \end{cases} ⎩ ⎨ ⎧dtdS=−βN′S×I+uN′−vSdtdI=βN′S×I−dI−vIdtdID=dIdtdND=vS+vI

其中，N′=S+IN' = S + IN′=S+I，取β=0.1\beta = 0.1β=0.1 ，d=0.01d=0.01d=0.01，μ=0.002\mu = 0.002μ=0.002 ，v=0.001v = 0.001v=0.001，利用 Matlab 可以得到：

matlab 复制代码 
clc;clear
TOTAL_N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun2',[1:500],[TOTAL_N-i0 i0 0 0]);  % 别忘了给ID和ND的初始值都为0
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(7)
% x的第一列是易感染者S的数量，x的第二列是患者I的数量
% x的第三列是患病死亡人数ID  ，x的第四列是自然死亡人数ND
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'k-',t,x(:,4),'g-','Linewidth',1.5)  
legend('易感染者S','患者I','患病死亡人数ID','自然死亡人数ND')
matlab 复制代码 
function dx=fun2(t,x)   % 大家可以修改里面的参数，来看结果的变化
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    d = 0.01;  % 得病的死亡率
    u = 0.002;  % 人口出生率
    v = 0.001;  % 自然死亡率
    % x(1)表示易感染者S  x(2)表示已感染者I  x(3)表示患病死亡人数ID  x(4)表示自然死亡人数ND
    dx = zeros(4,1);  
    dx(1) = - beta*x(1)*x(2)/(x(1)+x(2))+u*(x(1)+x(2)) - v*x(1) ;  
    dx(2) = beta*x(1)*x(2)/(x(1)+x(2)) -d*x(2)- v*x(2);
    dx(3) = d*x(2);
    dx(4) = v*x(1) + v*x(2);
end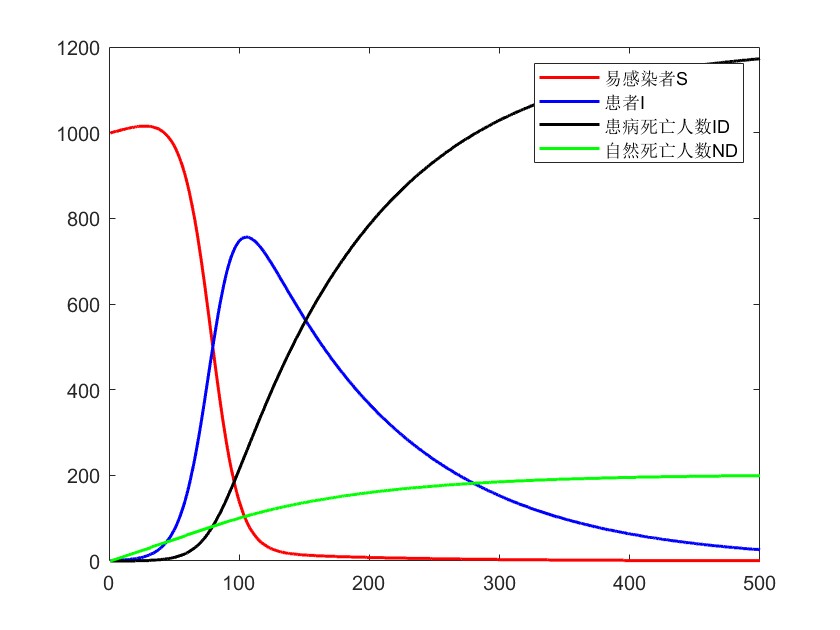

四、SIS 模型介绍

4.1 疾病特点

部分疾病（如流感病毒）具有"易治愈但易变异"的特性：感染恢复后不会产生抗体，未来仍可能再次患病，会呈现"感染→恢复为易感者→再感染"的循环过程

📌其状态转移图形为：

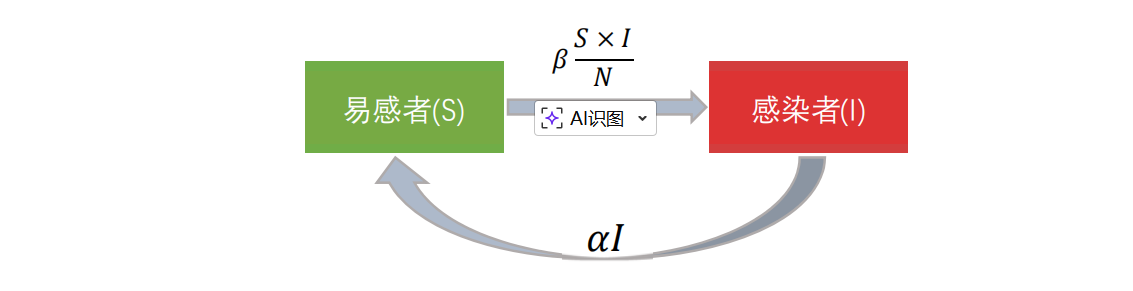
4.2 SIS模型的假设条件

  • 总人数固定为 NNN，不考虑因病死亡、自然出生/死亡的人口变化；
  • 单位时间内的新感染人数由βSIN\frac{\beta SI}{N}NβSI决定;
  • 感染状态 III 恢复为易感状态 SSS 的恢复率为 α\alphaα

4.3 对应的微分方程组

描述易感者( S )、感染者( I )随时间( t )变化的微分方程组为：
{dSdt=αI−βS×INdIdt=βS×IN−αI \begin{cases} \frac{\mathrm{d}S}{\mathrm{d}t} = \alpha I - \beta \frac{S \times I}{N} \\ \frac{\mathrm{d}I}{\mathrm{d}t} = \beta \frac{S \times I}{N} - \alpha I \end{cases} {dtdS=αI−βNS×IdtdI=βNS×I−αI

4.4 Matlab绘图

matlab 复制代码 
clc;clear
global TOTAL_N   % 定义总人数为全局变量（可以在子函数中使用）
TOTAL_N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun1',[1:500],[TOTAL_N-i0 i0]); 
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(1)
plot(t,x(:,1),'r-',t,x(:,2),'b-','Linewidth',1.5)   % x的第一列是易感染者S的数量，x的第二列是患者I的数量
legend('易感染者S','患者I')
matlab 复制代码 
function dx=fun1(t,x)   % 大家可以修改里面的参数，来看结果的变化
    global TOTAL_N   % 定义总人数为全局变量
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    alpha = 0.06; % 由感染状态I恢复为易感者状态S的恢复率
    dx = zeros(2,1);  % x(1)表示S  x(2)表示I
    dx(1) = alpha*x(2) - beta*x(1)*x(2)/TOTAL_N;  
    dx(2) = beta*x(1)*x(2)/TOTAL_N - alpha*x(2);
end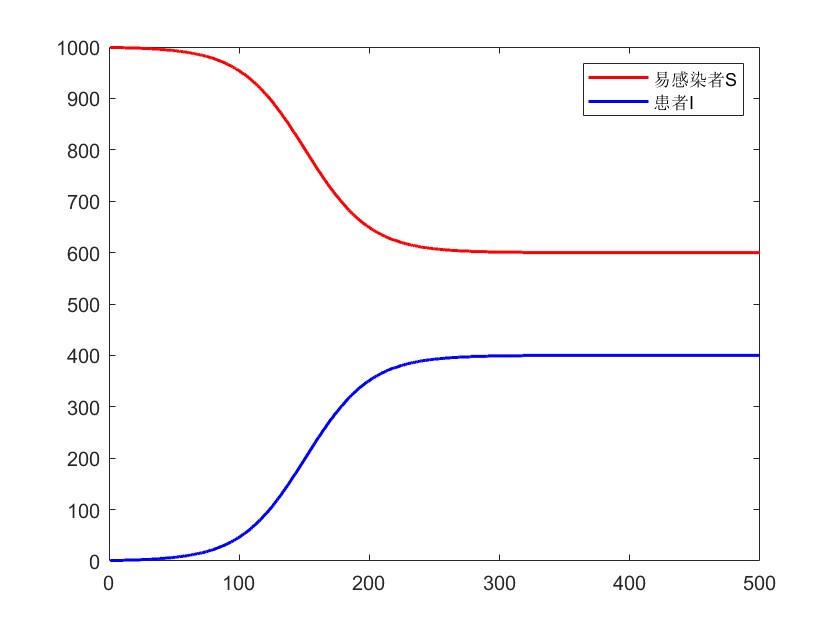

📌4.5 SIS 模型拓展

⭐考虑某种使得恢复率alpha增加的因素（例如建立医院、升级医疗装备等）

matlab 复制代码 
% 第200期后引入了新的医疗装备，使得恢复率alpha增加为原来的10倍
clc;clear
global TOTAL_N   % 定义总人数为全局变量（可以在子函数中使用）
TOTAL_N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun2',[1:500],[TOTAL_N-i0 i0]); 
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(2)
plot(t,x(:,1),'r-',t,x(:,2),'b-','Linewidth',1.5)   % x的第一列是易感染者S的数量，x的第二列是患者I的数量
legend('易感染者S','患者I')
axis([0 500 0 1000])  % 设置坐标轴范围，x轴为0-500 y轴为0-1000
matlab 复制代码 
function dx=fun2(t,x)   % 大家可以修改里面的参数，来看结果的变化
    global TOTAL_N   % 定义总人数为全局变量
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    alpha = 0.02; % 由感染状态I恢复为易感者状态S的恢复率
    if t > 200
        alpha = alpha * 10; % 第200期后引入了新的医疗装备，使得恢复率alpha增加为原来的10倍
    end
    dx = zeros(2,1);  % x(1)表示S  x(2)表示I
    dx(1) = alpha*x(2) - beta*x(1)*x(2)/TOTAL_N;  
    dx(2) = beta*x(1)*x(2)/TOTAL_N - alpha*x(2);
end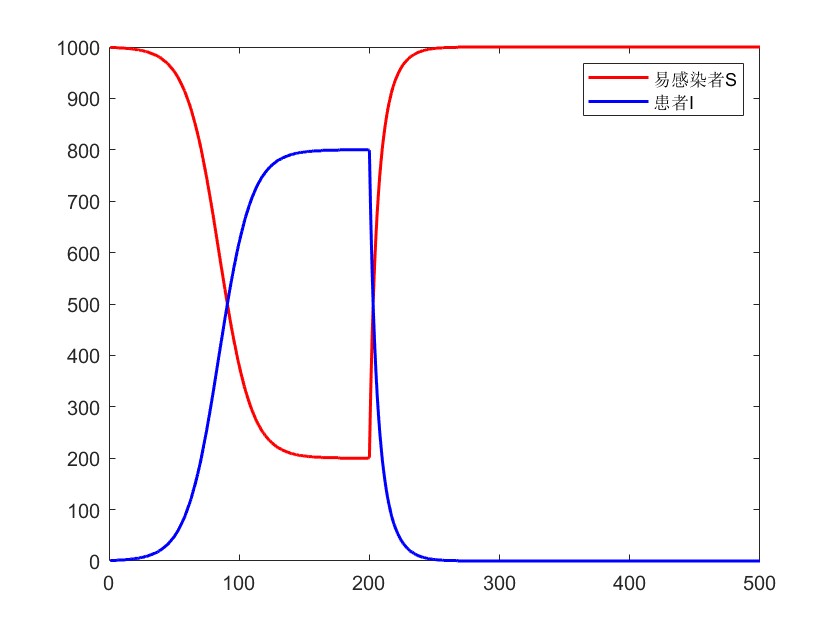

五、SIR 模型介绍

5.1 疾病特点

这类疾病（如天花、麻疹、腮腺炎）的核心特征是：发病迅速，且康复后会产生抗体，后续不会再被该疾病感染；📌其状态转移图形为：

5.2 SIR模型的假设与人群定义

  • 初始总人口数为NNN，不考虑因病死亡、自然出生/死亡的人口变化；
  • 模型包含三类人群：
    • SSS：易感者（尚未感染疾病的人群）；
    • III：感染者（正在患病的人群）；
    • RRR：康复者（已痊愈且体内含抗体、未来不会再感染的人群）；
  • 有效人群 N′N'N′：指传染病系统中可参与传播的人群（不含脱离系统的RRR），即N′=S+IN' = S + IN′=S+I

5.3 模型新增参数

  • γ\gammaγ：康复率 ，单位时间内从感染状态 III 康复为 RRR 的人群比例

📌模型对应的微分方程组

描述( S )、( I )、( R )随时间( t )变化的微分方程组为：
{dSdt=−βS×IN′dIdt=βS×IN′−γIdRdt=γI \begin{cases} \frac{\mathrm{d}S}{\mathrm{d}t} = -\beta \frac{S \times I}{N'} \\ \frac{\mathrm{d}I}{\mathrm{d}t} = \beta \frac{S \times I}{N'} - \gamma I \\ \frac{\mathrm{d}R}{\mathrm{d}t} = \gamma I \end{cases} ⎩ ⎨ ⎧dtdS=−βN′S×IdtdI=βN′S×I−γIdtdR=γI

5.4 Matlab绘图

matlab 复制代码 
clc;clear
N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun1',[1:500],[N-i0 i0 0]);   % 记得给康复者R一个初始值
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(1)
% x的第一列是易感染者S的数量，x的第二列是患者I的数量，x的第三列是康复者R的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-','Linewidth',1.5)  
legend('易感染者S','患者I','康复者R')
matlab 复制代码 
function dx=fun1(t,x)   % 大家可以修改里面的参数，来看结果的变化
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    gamma = 0.02;  % 康复率
    dx = zeros(3,1);  % x(1)表示S  x(2)表示I  x(3)表示R
    C = x(1)+x(2);  % 传染病系统中的有效人群,也就是课件中的N' = S+I
    dx(1) = - beta*x(1)*x(2)/C;  
    dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
    dx(3) = gamma*x(2); 
end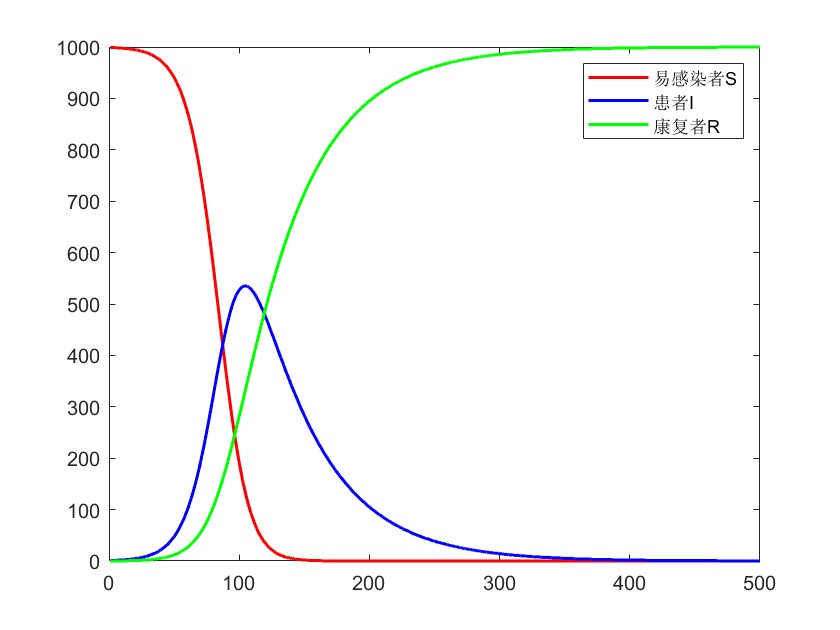

5.5 SIR 模型拓展

⭐考虑某种使得康复率gamma增加的因素（例如研发了疫苗、医疗设备升级等）

matlab 复制代码 
% 第100期后研发了疫苗，使得康复率增加为原来的10倍
clc;clear
N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun3',[1:200],[N-i0 i0 0]);   % 记得给康复者R一个初始值
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(3)
% x的第一列是易感染者S的数量，x的第二列是患者I的数量，x的第三列是康复者R的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-','Linewidth',1.5) 
legend('易感染者S','患者I','康复者R')
matlab 复制代码 
function dx=fun3(t,x)   % 大家可以修改里面的参数，来看结果的变化
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    gamma = 0.01;  % 康复率
    if t > 100
        gamma = gamma * 10;  % 第100期后研发了疫苗，使得康复率增加为原来的10倍
    end
    dx = zeros(3,1);  % x(1)表示S  x(2)表示I  x(3)表示R
    C = x(1)+x(2);  % 传染病系统中的有效人群,也就是课件中的N' = S+I
    dx(1) = - beta*x(1)*x(2)/C;  
    dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
    dx(3) = gamma*x(2); 
end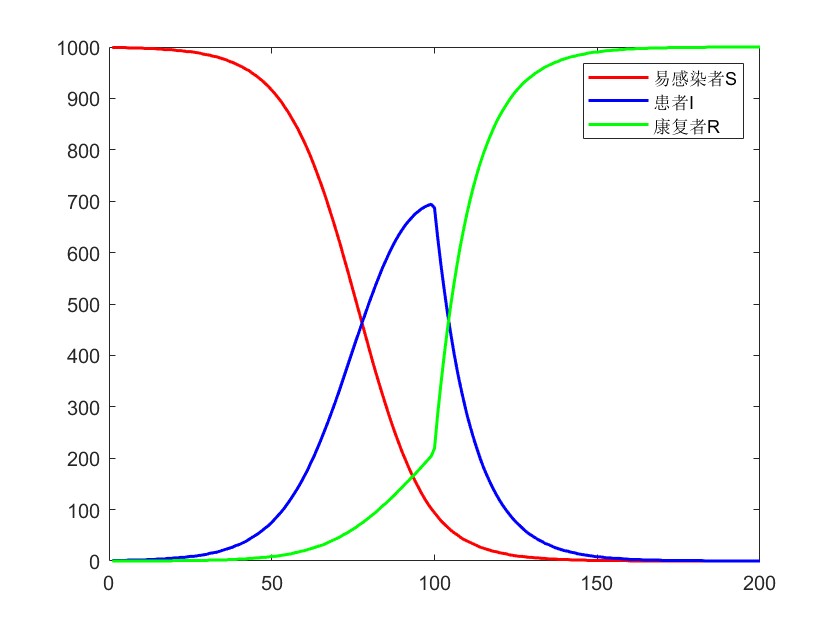

⭐考虑疾病的死亡率的SIR模型，不考虑人口正常出生率和死亡率，状态转移图为：

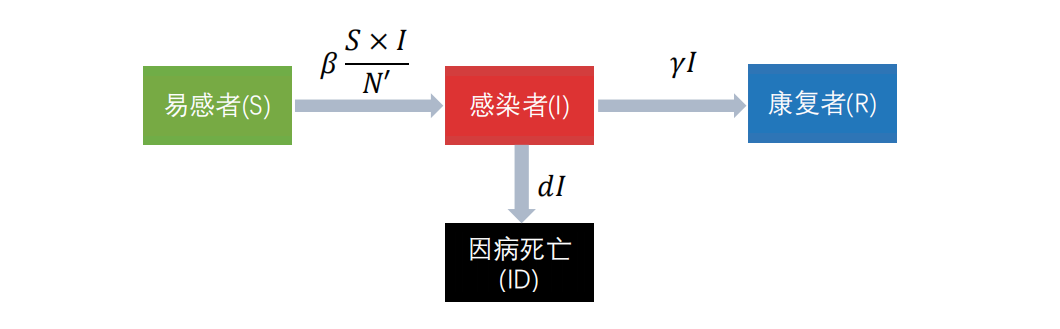
对应的微分方程组为：
{dSdt=−βS×IN′dIdt=βS×IN′−γI−dIdRdt=γIdIDdt=dI, 且 N′=S+I \begin{cases} \displaystyle \frac{\mathrm{dS}}{\mathrm{dt}} = -\beta \frac{\mathrm{S} \times \mathrm{I}}{\mathrm{N}'} \\[10pt] \displaystyle \frac{\mathrm{dI}}{\mathrm{dt}} = \beta \frac{\mathrm{S} \times \mathrm{I}}{\mathrm{N}'} - \gamma \mathrm{I} - \mathrm{dI} \\[10pt] \displaystyle \frac{\mathrm{dR}}{\mathrm{dt}} = \gamma \mathrm{I} \\[10pt] \displaystyle \frac{\mathrm{dID}}{\mathrm{dt}} = \mathrm{dI} \end{cases} ,\ \text{且}\ \mathrm{N}' = \mathrm{S} + \mathrm{I} ⎩ ⎨ ⎧dtdS=−βN′S×IdtdI=βN′S×I−γI−dIdtdR=γIdtdID=dI, 且 N′=S+I

matlab 复制代码 
clc;clear
N = 1000;  % 总人数
i0 = 1; % 初始时刻患者（已感染者）的人数
[t,x]=ode45('fun4',[1:400],[N-i0 i0 0 0]);   % 记得给患病死亡人数ID一个初始值
x = round(x);  % 对x进行四舍五入(人数为整数)
figure(4)
% x的第一列是易感染者S的数量，x的第二列是患者I的数量
% x的第三列是康复者R的数量, x的第四列是患病死亡人数ID的数量
plot(t,x(:,1),'r-',t,x(:,2),'b-',t,x(:,3),'g-',t,x(:,4),'k-','Linewidth',1.5)   
legend('易感染者S','患者I','康复者R','患病死亡人数ID')
matlab 复制代码 
function dx=fun4(t,x)   % 大家可以修改里面的参数，来看结果的变化
    beta = 0.1;  % 易感染者与已感染者接触且被传染的强度
    gamma = 0.02;  % 康复率
    d = 0.005; % 因病的死亡率
    dx = zeros(4,1);  % x(1)表示S  x(2)表示I  x(3)表示R  x(4)表示ID
    C = x(1)+x(2);  % 传染病系统中的有效人群,也就是课件中的N' = S+I
    dx(1) = - beta*x(1)*x(2)/C;  
    dx(2) = beta*x(1)*x(2)/C - gamma*x(2) -d*x(2);
    dx(3) = gamma*x(2);
    dx(4) = d*x(2);
end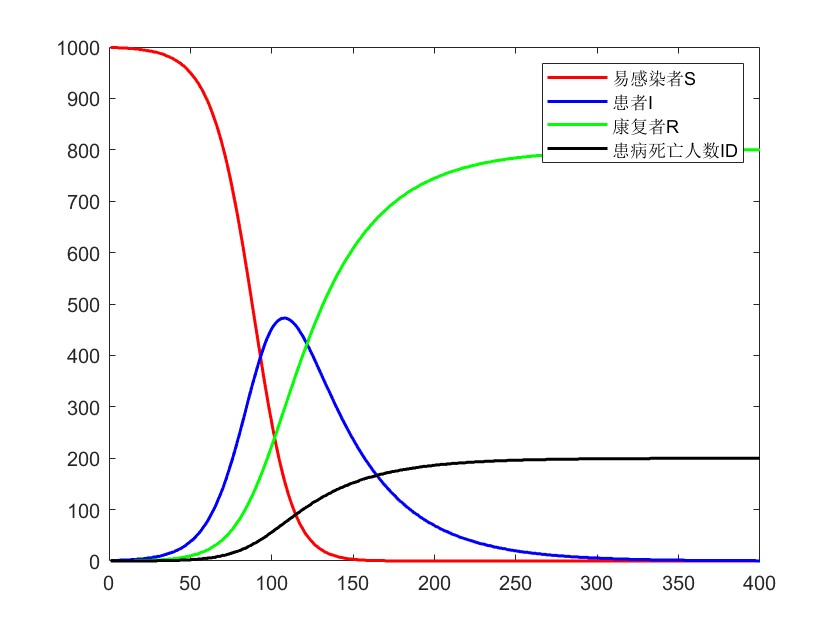

📌参考文献：@数学建模清风

相关推荐
qianbo_insist3 天前
基于APAP算法的图像和视频拼接
算法·数学建模·图像拼接
万行4 天前
机器学习&第三章
人工智能·python·机器学习·数学建模·概率论
打点计时器4 天前
初见波动方程和贝塞尔函数
数学建模·信号处理
民乐团扒谱机4 天前
【微实验】基于MATLAB的一维条材下料优化问题求解
数学建模·matlab·线性规划·最优化模型·整数线性规划
湘-枫叶情缘4 天前
重生1995：我的数学模型能暴击-第二集: 设备报废危机？一张纸预测未来 !
科技·数学建模·产品运营
Heorine5 天前
数学建模 绘图 图表 可视化（6）
python·数学建模·数据可视化
ECT-OS-JiuHuaShan6 天前
哲学第三次世界大战：《易经》递归生成论打破西方机械还原论
人工智能·程序人生·机器学习·数学建模·量子计算
进击中的小龙6 天前
基于rtklib的载波相位平滑伪距
c语言·算法·数学建模·gitee
墨有6666 天前
数学分析栈的出栈顺序：从算法判断到数学本质（卡特兰数初探）
c++·算法·数学建模
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03Labelme从安装到标注：零基础完整指南04Claude Code Skills 实用使用手册05AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南062025年大语言模型技术全景报告07UV安装并设置国内源08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09网站改了域名，如何查找？10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）