一、线性定常齐次状态方程的解
1、系统状态空间表达式的解的定义

2、零输入响应与零状态响应
(1)零输入响应:


(2)零状态响应:

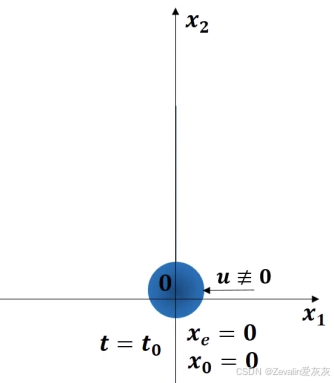
(3)全响应:

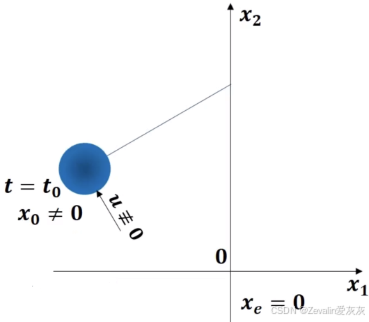
3、求解线性定常齐次状态方程的解
(1)线性定常齐次状态方程的解就是对应系统在非平衡初始状态作用下的运动轨迹,也称为系统的零输入响应。
(2)线性定常齐次状态方程的解的形式:


(3)线性定常系统零输入响应的几点说明:

4、矩阵指数函数的性质

5、矩阵指数函数的计算方法

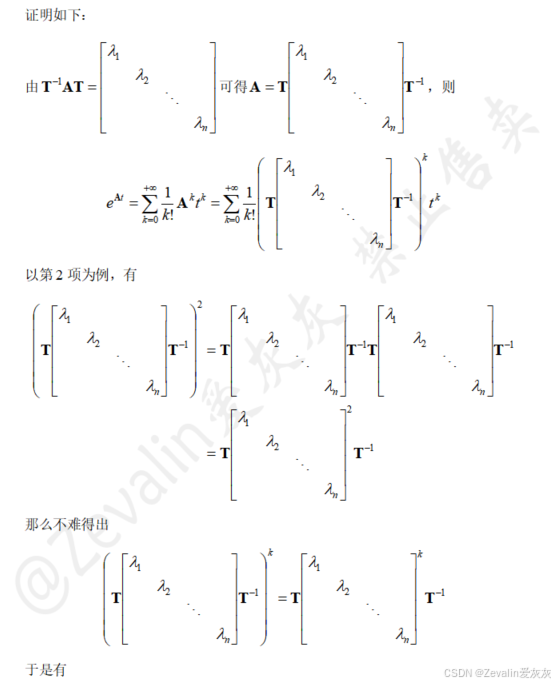


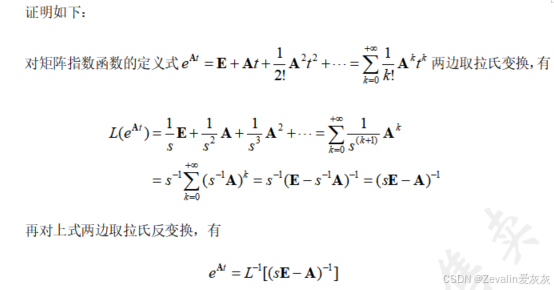






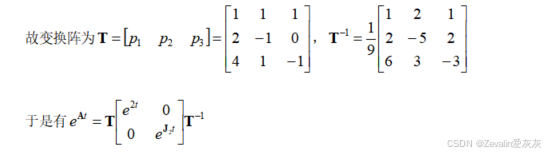


二、状态转移矩阵
1、状态转移矩阵的定义
(1)为了更好地描述系统状态在状态空间中的转移,引入状态转移矩阵,本节先介绍线性定常系统的状态转移矩阵,线性时变系统的状态转移矩阵将在第四节介绍。
(2)状态转移矩阵的定义与表示:

(3)系统的零输入响应也可用状态转移矩阵表示:
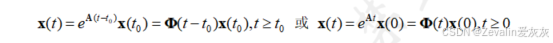
(4)状态转移矩阵的物理意义:

2、状态转移矩阵的性质




3、状态转移矩阵的算法
(1)状态转移矩阵的本质也是一个矩阵指数函数,那么其求解方法也与矩阵指数函数的求解相同。
(2)举例:

三、线性定常系统非齐次状态方程的解
1、零状态响应的表示
(1)结论:
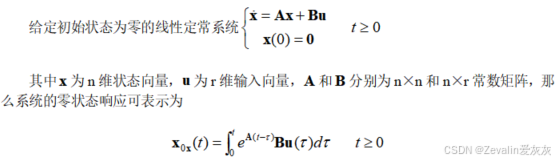
(2)证明:
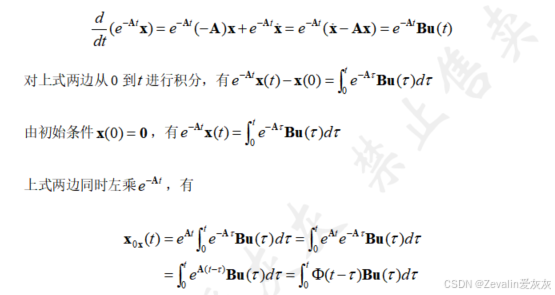
2、线性定常非齐次状态方程的解的形式

3、线性定常系统的响应
(1)脉冲输入的响应:
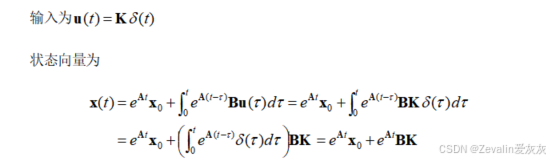
(2)阶跃输入的响应:
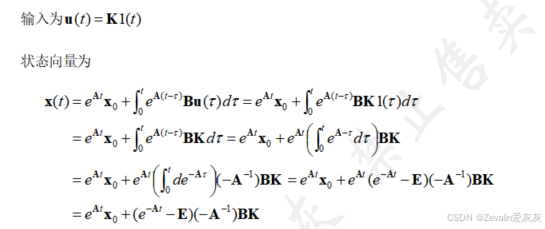
(3)斜坡输入的响应:
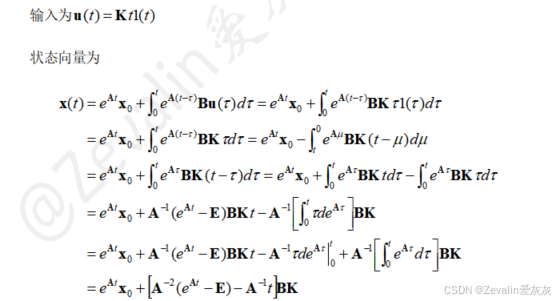
四、线性时变系统的解
1、时变系统状态方程解的特点

2、线性时变系统齐次方程的解



3、线性时变系统非齐次方程的解
(1)线性时变系统非齐次方程的解的形式:

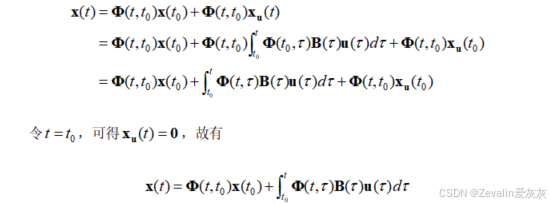
(2)由于通常情况下,封闭形式的状态转移矩阵很难求得,所以上式的意义不在于计算的应用,而在于系统理论研究中的应用。