题目:Point-SRA: Self-Representation Alignment for 3D Representation Learning
题目:Point-SRA:面向 3D 表征学习的自表征对齐方法
Self-Representation 自表征
Alignment 对齐
3D Representation Learning 三维表征学习
Abstract 摘要
掩码自编码器(MAE)已成为3D表征学习的主流范式,在各类下游任务中刷新了性能基准。现有方法采用固定掩码率,既忽略了多尺度表征关联与内在几何结构,又依赖逐点重建的假设------这与点云的多样性存在冲突。
为解决这些问题,我们提出一种3D表征学习方法Point-SRA ,通过自蒸馏与概率建模实现表征对齐。具体而言:我们为MAE分配不同掩码率,以捕捉互补的几何与语义信息;同时,MeanFlow Transformer(MFT) 利用跨模态条件嵌入,实现多样化的概率重建。
我们的分析进一步发现,MFT不同时间步的表征也具有互补性。因此,我们在MAE与MFT两个层面提出双自表征对齐机制 。最终,我们设计了流场条件微调架构 ,以充分利用MeanFlow所学习的点云分布。
在ScanObjectNN数据集上,Point-SRA较Point-MAE性能提升5.37%;在颅内动脉瘤分割任务中,动脉的平均IoU达96.07%、动脉瘤达86.87%;在3D目标检测任务中,Point-SRA的AP@50达47.3%,超过MaskPoint 5.12%。
1. Introduction 引言
掩码自编码器(MAE)已成为自监督表征学习(SSRL)领域的主流框架。在3D领域中,Point-MAE(Pang等,2022)、Point-M2AE(Zhang等,2022)、MaskPoint(Liu、Cai与Lee,2022)等方法已成功适配该范式,并在各类任务中取得了优异性能。通过从稀疏的可见点重建掩码区域,3D MAE能够学习到鲁棒的几何表征,具备出色的泛化能力。
尽管效果显著,但现有方法大多基于经验设置采用固定掩码率 ,缺乏对"掩码率如何影响学习到的表征"的理论洞察。这引出了一个关键但尚未充分探索的问题:不同掩码率是否会天然产生丰富度各异的表征?这些差异能否被利用以提升整体表征质量?
我们的研究揭示了一个核心原则:掩码率互补性 。如图1所示,我们发现掩码率的选择会在"几何细节保留"与"语义抽象"之间形成系统性权衡。具体而言,随着掩码率升高,与输入的互信息减少,而语义压缩能力增强,最终使表征捕捉到3D结构的不同层面:低掩码率(≤30%)擅长保留细粒度几何特征,高掩码率(≥75%)则迫使模型学习抽象的语义模式。这种互补性并非偶然,而是掩码带来的信息瓶颈所固有的属性。
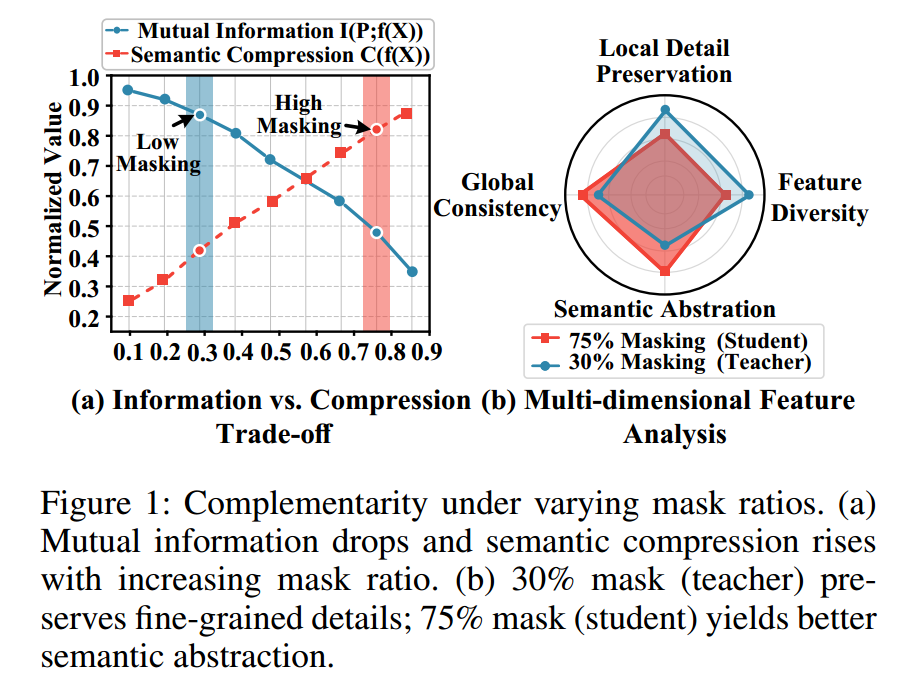
然而,当前3D MAE方法存在两个根本局限,阻碍了其有效利用掩码率互补性:
- 固定掩码策略限制了模型从不同掩码率下的互补表征中获益的能力;
- 在高掩码率下,3D MAE中的逐点确定性重建常出现失配问题------它无法适配点云固有的结构多样性。如图2所示,同一可见区域可能对应多种合理的重建结果。
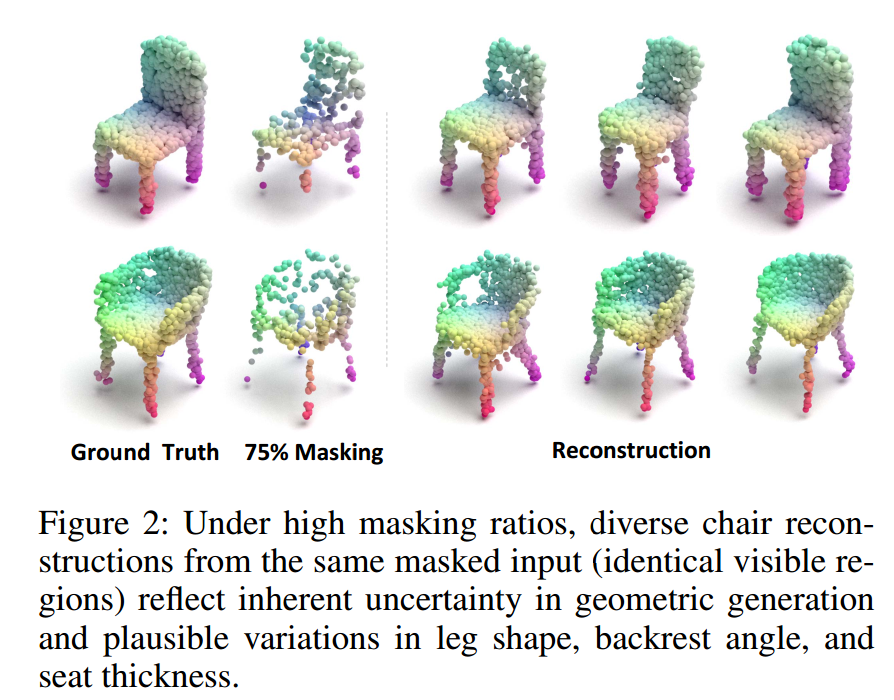
为充分利用所发现的掩码率互补性,我们引入自表征对齐(SRA)作为内部知识迁移机制。同时,我们研究了MeanFlow的概率重建能力,并分析了不同时间步的表征信息。为此,我们设计了 MeanFlow Transformer(MFT)以有效利用这些特性。此外,MeanFlow的概率公式适配了3D重建的多解性:基于轨迹的学习过程能够对齐不同时间状态的表征,而其对条件生成的支持则允许灵活融入多模态信息。
因此,我们设计了双自表征对齐(Dual SRA)机制:
- MAE层面自表征对齐(MAE-SRA):整合不同掩码率下得到的表征,促进几何与语义知识的融合;
- MFT层面自表征对齐(MFT-SRA) :利用MeanFlow学习到的轨迹,对齐不同时间步的表征,捕捉点云分布的演化规律。
最终,我们提出了Point-SRA框架 ,系统性地挖掘3D表征学习中的掩码率互补性。此外,我们通过整合基于MeanFlow的更新,增强了标准Transformer微调网络。
我们的主要贡献总结如下: - 对掩码率互补性、重建不确定性与MeanFlow的数值稳定性进行了系统性理论分析,并基于这些洞见设计了Point-SRA框架;
- 提出统一的Dual SRA机制,对齐不同掩码率与时间状态下的表征,实现完全自包含的知识迁移;
- 提出MFT以解决3D MAE中逐点重建的局限,实现表征引导与概率重建;
- 开发流场条件微调架构,利用预训练阶段学习到的分布知识提升下游任务性能。
2. Observations 观察
点云 P ∈ R N × 3 \mathcal{P} \in \mathbb{R}^{N \times 3} P∈RN×3通过最远点采样(FPS)被划分为 G G G个局部区域 N 1 , N 2 , . . . , N G \mathcal{N}_1, \mathcal{N}_2, ..., \mathcal{N}_G N1,N2,...,NG。随机选取 ⌊ r ⋅ G ⌋ \lfloor r \cdot G \rfloor ⌊r⋅G⌋个区域进行掩码(其中掩码率 r ∈ [ 0 , 1 ] r \in [0,1] r∈[0,1]),用 V \mathcal{V} V表示可见区域的索引集合,则可见区域可表示为 X r = { N i : i ∈ V } \mathcal{X}_r = \{\mathcal{N}i : i \in \mathcal{V}\} Xr={Ni:i∈V}。编码器 f θ r : X r → R d f{\theta_r}: \mathcal{X}_r \to \mathbb{R}^d fθr:Xr→Rd将可见区域映射到 d d d维表征空间。
2.1 Theorem A: Masking Ratio Complementarity 定理A:掩码率互补性
对于掩码率 r l < r h r_l < r_h rl<rh,在信息瓶颈框架下,对应的最优编码器 f θ l ∗ f_{\theta_l}^* fθl∗和 f θ h ∗ f_{\theta_h}^* fθh∗满足:
I ( P ; f θ l ∗ ( X r l ) ) > I ( P ; f θ h ∗ ( X r h ) ) , (1) \mathcal{I}(\mathcal{P}; f_{\theta_l}^*(\mathcal{X}{r_l})) > \mathcal{I}(\mathcal{P}; f{\theta_h}^*(\mathcal{X}{r_h})), \tag{1} I(P;fθl∗(Xrl))>I(P;fθh∗(Xrh)),(1)
C ( f θ h ∗ ( X r h ) ) > C ( f θ l ∗ ( X r l ) ) , (2) \mathcal{C}(f{\theta_h}^*(\mathcal{X}{r_h})) > \mathcal{C}(f{\theta_l}^*(\mathcal{X}_{r_l})), \tag{2} C(fθh∗(Xrh))>C(fθl∗(Xrl)),(2)
其中 I ( ⋅ ; ⋅ ) \mathcal{I}(\cdot;\cdot) I(⋅;⋅)表示互信息, C ( ⋅ ) \mathcal{C}(\cdot) C(⋅)表示语义压缩度,其定义为:
C ( Z ) = H ( Z ) I ( P semantic ; Z ) , (3) \mathcal{C}(Z) = \frac{\mathcal{H}(Z)}{\mathcal{I}(\mathcal{P}_{\text{semantic}}; Z)}, \tag{3} C(Z)=I(Psemantic;Z)H(Z),(3)
P semantic \mathcal{P}_{\text{semantic}} Psemantic代表点云的语义信息, H ( Z ) \mathcal{H}(Z) H(Z)是表征 Z Z Z的熵。详细证明见补充材料。
2.2 Corollary: Representation Complementarity 推论:表征互补性
存在投影函数 π geo : R d → R d geo \pi_{\text{geo}}: \mathbb{R}^d \to \mathbb{R}^{d_{\text{geo}}} πgeo:Rd→Rdgeo和 π sem : R d → R d sem \pi_{\text{sem}}: \mathbb{R}^d \to \mathbb{R}^{d_{\text{sem}}} πsem:Rd→Rdsem,使得:
∥ π geo ( f θ l ∗ ( X r l ) ) − π geo ( P ) ∥ F < ∥ π geo ( f θ h ∗ ( X r h ) ) − π geo ( P ) ∥ F , (4) \left\| \pi_{\text{geo}}(f_{\theta_l}^*(\mathcal{X}{r_l})) - \pi{\text{geo}}(\mathcal{P}) \right\|F < \left\| \pi{\text{geo}}(f_{\theta_h}^*(\mathcal{X}{r_h})) - \pi{\text{geo}}(\mathcal{P}) \right\|F, \tag{4} πgeo(fθl∗(Xrl))−πgeo(P) F< πgeo(fθh∗(Xrh))−πgeo(P) F,(4)
∥ π sem ( f θ h ∗ ( X r h ) ) − π sem ( P ) ∥ F < ∥ π sem ( f θ l ∗ ( X r l ) ) − π sem ( P ) ∥ F , (5) \left\| \pi{\text{sem}}(f_{\theta_h}^*(\mathcal{X}{r_h})) - \pi{\text{sem}}(\mathcal{P}) \right\|F < \left\| \pi{\text{sem}}(f_{\theta_l}^*(\mathcal{X}{r_l})) - \pi{\text{sem}}(\mathcal{P}) \right\|_F, \tag{5} πsem(fθh∗(Xrh))−πsem(P) F< πsem(fθl∗(Xrl))−πsem(P) F,(5)
这为我们的双自表征对齐(Dual SRA)机制提供了理论基础,表明高掩码率有助于保留语义信息,而低掩码率则更易保留几何信息。
2.3 Theorem B: Reconstruction Uncertainty 定理B:重建不确定性
传统MAE方法基于逐点重建假设,即存在唯一的最优重建目标:
L det = E P ∼ p data [ ∥ P M − G e n ( P V ) ∥ 2 ] , (6) \mathcal{L}{\text{det}} = \mathbb{E}{\mathcal{P} \sim p_{\text{data}}} \left[ \left\| \mathcal{P}M - G{en}(\mathcal{P}_V) \right\|^2 \right], \tag{6} Ldet=EP∼pdata[∥PM−Gen(PV)∥2],(6)
其中 G e n G_{en} Gen是生成函数, P M \mathcal{P}_M PM和 P V \mathcal{P}_V PV分别表示掩码区域和可见区域。然而,点云几何重建本质上具有模糊性:给定可见区域 P V \mathcal{P}_V PV,掩码区域的合理构型构成一个条件概率分布:
p ( P M ∣ P V ) = ∫ Θ p ( P M ∣ P V , ω ) p ( ω ∣ P V ) d ω , (7) p(\mathcal{P}_M | \mathcal{P}V) = \int{\Theta} p(\mathcal{P}_M | \mathcal{P}_V, \omega) p(\omega | \mathcal{P}_V) d\omega, \tag{7} p(PM∣PV)=∫Θp(PM∣PV,ω)p(ω∣PV)dω,(7)
其中 Θ \Theta Θ代表曲率、密度等几何参数。当掩码率处于合理范围时,重建分布的熵满足:
H ( p ( P M ∣ P V ) ) > 0. (8) H(p(\mathcal{P}_M | \mathcal{P}_V)) > 0. \tag{8} H(p(PM∣PV))>0.(8)
因此,我们采用MeanFlow来学习从噪声分布到真实数据分布的连续变换,它能够处理几何不确定性,并生成多样且几何一致的重建结果。
3. Methodology 方法论
3.1 Network Architecture 网络架构 (MAE&MFT)
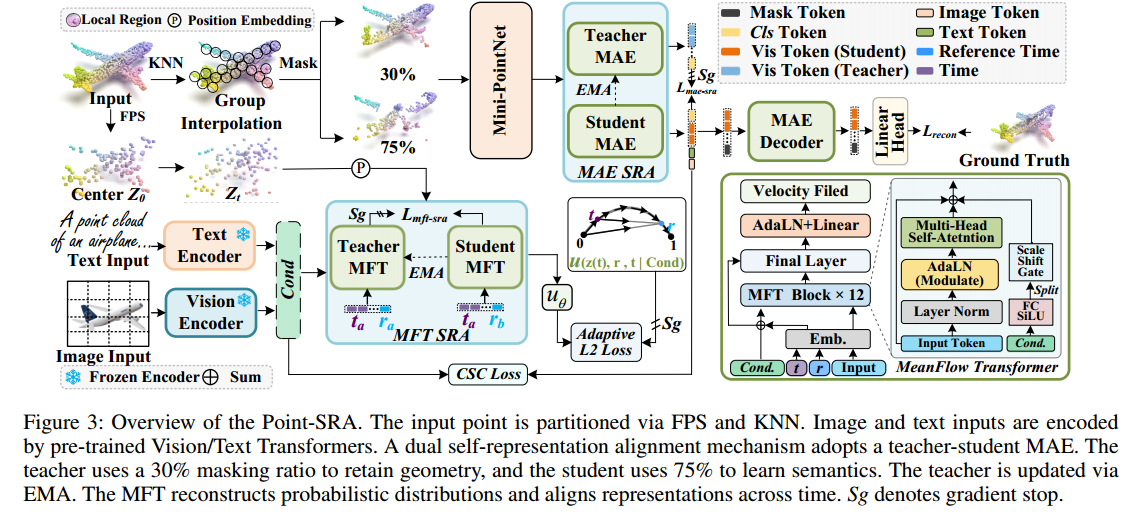
如图3所示,本文提出的Point-SRA框架包含四个紧密集成的组件,它们协同工作以增强三维表示。
①MAE模块作为基础模块,通过重构输入的掩码区域来学习几何特征。
②为解决点云几何中固有的模糊性,MFT模块被设计为通过连续的概率轨迹对数据分布进行建模,从而更有效地捕捉几何不确定性。
③构建在这两个模块之上,MAE-SRA会对齐不同掩码比例下得到的特征表示,实现几何细节与语义抽象的融合。
④此外,MFT-SRA会对齐不同时间状态下的概率流表示,使模型能够捕捉分布的动态演变。
3.1.1 MAE MAE模块
首先执行掩码操作,随机保留一个可见点子集 P v i s = { p i ∣ M ( p i ) = 0 } \mathcal{P}{vis} = \{p_i | \mathcal{M}(p_i) = 0\} Pvis={pi∣M(pi)=0},其余点则被掩码为 P m a s k = { p i ∣ M ( p i ) = 1 } \mathcal{P}{mask} = \{p_i | \mathcal{M}(p_i) = 1\} Pmask={pi∣M(pi)=1}。
编码器 E M A E E_{MAE} EMAE对可见点进行处理,以提取其特征表示:
h v i s = E M A E ( P v i s ) (9) h_{vis} = E_{MAE}(\mathcal{P}_{vis}) \tag{9} hvis=EMAE(Pvis)(9)
同时,为掩码点生成可学习的掩码标记,并将其与可见特征拼接,形成完整的特征集 h f u l l h_{full} hfull。解码器 D M A E D_{MAE} DMAE以该完整表示为输入,重构所有点的坐标 P ^ \hat{\mathcal{P}} P^:
P ^ = D M A E ( h f u l l ) (10) \hat{\mathcal{P}} = D_{MAE}(h_{full}) \tag{10} P^=DMAE(hfull)(10)
为提升重构质量,采用Chamfer Distance倒角距离
(Fan、Su与Guibas,2017)作为重构损失:
L r e c o n = 1 ∣ P ∣ ∑ p i ∈ P min q j ∈ P ^ ∥ p i − q j ∥ 2 2 + 1 ∣ P ^ ∣ ∑ q j ∈ P ^ min p i ∈ P ∥ q j − p i ∥ 2 2 (11) \begin{aligned} \mathcal{L}{recon} &= \frac{1}{|\mathcal{P}|} \sum{p_i \in \mathcal{P}} \min_{q_j \in \hat{\mathcal{P}}} \| p_i - q_j \|2^2 \\ &\quad + \frac{1}{|\hat{\mathcal{P}}|} \sum{q_j \in \hat{\mathcal{P}}} \min_{p_i \in \mathcal{P}} \| q_j - p_i \|_2^2 \end{aligned} \tag{11} Lrecon=∣P∣1pi∈P∑qj∈P^min∥pi−qj∥22+∣P^∣1qj∈P^∑pi∈Pmin∥qj−pi∥22(11)
其中, p i p_i pi表示来自真实点云的点, q j q_j qj表示来自预测点云的点。
3.1.2 Conditional Distribution Modeling with MeanFlow 基于MeanFlow的条件分布建模
给定一个点云及其关联的多模态条件信息(包括图像特征 f i m g f_{img} fimg和文本特征 f t e x t f_{text} ftext)。
首先利用专用的图像与文本编码器提取条件表示。随后定义一条连续轨迹 { z t } t ∈ [ 0 , 1 ] \{z_t\}_{t \in [0,1]} {zt}t∈[0,1]:其中 z 0 z_0 z0是目标点云, z 1 z_1 z1 从标准正态分布中采样。该轨迹通过线性插值构建:
z t = ( 1 − t ) ⋅ z 0 + t ⋅ z 1 (12) z_t = (1-t) \cdot z_0 + t \cdot z_1 \tag{12} zt=(1−t)⋅z0+t⋅z1(12)
接下来,采用MeanFlow方法预测该轨迹上的平均速度场。给定当前时间步 t t t和参考时间步 r r r(满足 r < t r < t r<t),MeanFlow将 t t t到 r r r 的参考速度估计为:
u θ ( z t , r , t ∣ c ) ≈ z r − z t r − t (13) u_\theta(z_t, r, t|c) \approx \frac{z_r - z_t}{r - t} \tag{13} uθ(zt,r,t∣c)≈r−tzr−zt(13)
其中 c c c表示融合了多模态信息的条件特征向量,其构造方式如下:
c = e t ( t ) + e r ( r ) + W i m g f i m g + W t e x t f t e x t (14) c = e_t(t) + e_r(r) + W_{img}f_{img} + W_{text}f_{text} \tag{14} c=et(t)+er(r)+Wimgfimg+Wtextftext(14)
这里 e t ( ⋅ ) e_t(\cdot) et(⋅)和 e r ( ⋅ ) e_r(\cdot) er(⋅)是时间嵌入函数, W i m g 、 W t e x t W_{img}、W_{text} Wimg、Wtext是投影矩阵。
MFT被用作骨干网络以预测平均速度场(如图3所示),对应的损失为:
L M F M = E t , r , z t , z r , c [ ∥ u θ ( z t , r , t ∣ c ) − u t a r g e t ∥ 2 ] (15) \mathcal{L}{MFM} = \mathbb{E}{t,r,z_t,z_r,c} \left[ \| u_\theta(z_t, r, t|c) - u_{target} \|^2 \right] \tag{15} LMFM=Et,r,zt,zr,c[∥uθ(zt,r,t∣c)−utarget∥2](15)
目标速度 u t a r g e t u_{target} utarget由理论原理推导而来:不仅考虑了基本的有限差分 z r − z t r − t \frac{z_r - z_t}{r - t} r−tzr−zt,还融入了瞬时速度场的时间导数:
u t a r g e t = v t − ( t − r ) ⋅ d d t v t ( z t ) (16) u_{target} = v_t - (t - r) \cdot \frac{d}{dt} v_t(z_t) \tag{16} utarget=vt−(t−r)⋅dtdvt(zt)(16)
其中 v t = z 1 − z 0 v_t = z_1 - z_0 vt=z1−z0,时间导数 d d t v t ( z t ) \frac{d}{dt} v_t(z_t) dtdvt(zt)通过雅可比向量积(JVP)计算:
d d t v t ( z t ) = ∇ z t v t ( z t ) ⋅ v t ( z t ) + ∂ v t ( z t ) ∂ t (17) \frac{d}{dt} v_t(z_t) = \nabla_{z_t} v_t(z_t) \cdot v_t(z_t) + \frac{\partial v_t(z_t)}{\partial t} \tag{17} dtdvt(zt)=∇ztvt(zt)⋅vt(zt)+∂t∂vt(zt)(17)
为稳定训练,我们采用自适应L2损失:它会根据预测误差动态调整损失权重:
L M F M = E [ s g ( w ) ⋅ ∥ u θ − u t a r g e t ∥ 2 ] (18) \mathcal{L}{MFM} = \mathbb{E} \left[ sg(w) \cdot \| u\theta - u_{target} \|^2 \right] \tag{18} LMFM=E[sg(w)⋅∥uθ−utarget∥2](18)
其中 w = 1 ( ∥ u θ − u t a r g e t ∥ 2 + ϵ ) p w = \frac{1}{(\| u_\theta - u_{target} \|^2 + \epsilon)^p} w=(∥uθ−utarget∥2+ϵ)p1, s g ( ⋅ ) sg(\cdot) sg(⋅)表示停止梯度操作, p = 1 − γ p = 1 - \gamma p=1−γ是幂指数, ϵ \epsilon ϵ是用于数值稳定性的小常数; u θ u_\theta uθ 是MFT预测的平均速度场, u t a r g e t u_{target} utarget是通过MeanFlow恒等式计算的理论目标。
3.1.3 Cross-modal Joint Conditioning 跨模态联合条件控制
点云的几何特征通过MAE编码器提取,而图像和文本特征则分别由ImageTransformer和TextTransformer获取。这些特征在模块间的传递方式如下:
f img-token = W img ( f cls ) , (19) f_{\text{img-token}} = W_{\text{img}}(f_{\text{cls}}), \tag{19} fimg-token=Wimg(fcls),(19)
f text-token = W text ( f cls ) , (20) f_{\text{text-token}} = W_{\text{text}}(f_{\text{cls}}), \tag{20} ftext-token=Wtext(fcls),(20)
其中 f cls f_{\text{cls}} fcls表示MAE编码器输出的 [CLS] \text{[CLS]} [CLS] token特征, W img W_{\text{img}} Wimg、 W text W_{\text{text}} Wtext为线性投影矩阵。
为了对齐点云编码器的表示与图像、文本模态的表示,我们定义了跨模态语义一致性(CSC)损失 :
L CSC = L SmoothL1 ( f img-token , f img ) (21) \mathcal{L}{\text{CSC}} = \mathcal{L}{\text{SmoothL1}}(f_{\text{img-token}}, f_{\text{img}}) \tag{21} LCSC=LSmoothL1(fimg-token,fimg)(21)
- L SmoothL1 ( f text-token , f text ) . \quad\quad\quad + \mathcal{L}{\text{SmoothL1}}(f{\text{text-token}}, f_{\text{text}}). +LSmoothL1(ftext-token,ftext).
3.1.4 Dual Self-Representation Alignment 双重自表示对齐
如图3所示,自表示对齐(SRA) 同时应用于MAE层与MFT层,以促进有效的知识迁移。
教师模型的参数通过指数移动平均(EMA)从学生模型更新:
θ teacher ← m ⋅ θ teacher + ( 1 − m ) ⋅ θ student (22) \theta_{\text{teacher}} \leftarrow m \cdot \theta_{\text{teacher}} + (1 - m) \cdot \theta_{\text{student}} \tag{22} θteacher←m⋅θteacher+(1−m)⋅θstudent(22)
其中 m ∈ [ 0 , 1 ] m \in [0,1] m∈[0,1]是控制更新速率的动量系数。
3.2 Network Architecture 网络架构 (MAE-SRA&MFT-SRA)
3.2.1 MAE-SRA MAE-SRA模块
在MAE层构建了师生架构:学生模型采用高掩码率训练,教师模型采用低掩码率训练。
具体而言,我们应用两种掩码模式 M h \mathcal{M}_h Mh和 M l \mathcal{M}_l Ml(分别对应高、低掩码率),得到掩码输入 P h \mathcal{P}_h Ph 和 P l \mathcal{P}_l Pl。
学生模型处理高掩码输入:
h student = E MAE ( P h ) (23) h_{\text{student}} = E_{\text{MAE}}(\mathcal{P}_h) \tag{23} hstudent=EMAE(Ph)(23)
教师模型处理低掩码输入:
h teacher = E MAE EMA ( P l ) (24) h_{\text{teacher}} = E_{\text{MAE}}^{\text{EMA}}(\mathcal{P}_l) \tag{24} hteacher=EMAEEMA(Pl)(24)
其中 E MAE EMA E_{\text{MAE}}^{\text{EMA}} EMAEEMA表示教师编码器。
MAE-SRA损失定义为学生与教师模型特征表示之间的余弦相似度损失:
L mae-sra = 1 − h student ⋅ h teacher ∣ h student ∣ ⋅ ∣ h teacher ∣ (25) \mathcal{L}{\text{mae-sra}} = 1 - \frac{h{\text{student}} \cdot h_{\text{teacher}}}{|h_{\text{student}}| \cdot |h_{\text{teacher}}|} \tag{25} Lmae-sra=1−∣hstudent∣⋅∣hteacher∣hstudent⋅hteacher(25)
3.2.2 MFT-SRA MFT-SRA模块
在MFT层,设计了一种时间对齐策略,用于对齐不同时间点的表示并捕捉概率流的演变。
具体而言,我们选取两个不同的时间步 t a > t b t_a > t_b ta>tb:学生模型在 t a t_a ta处处理表示,教师模型在 t b t_b tb处处理。
给定条件 c c c 以及对应的含噪点云状态 z t a z_{t_a} zta和 z t b z_{t_b} ztb,提取的特征表示为:
h t a = F M F ( z t a , t a , c ) , h t b = F M F EMA ( z t b , t b , c ) (26) h_{t_a} = F_{MF}(z_{t_a}, t_a, c), \, h_{t_b} = F_{MF}^{\text{EMA}}(z_{t_b}, t_b, c) \tag{26} hta=FMF(zta,ta,c),htb=FMFEMA(ztb,tb,c)(26)
其中 F M F F_{MF} FMF和 F M F EMA F_{MF}^{\text{EMA}} FMFEMA分别表示学生与教师MFT网络的特征提取器。
MFT-SRA损失定义为这两个表示之间的余弦相似度损失:
L m f t − s r a = ∥ h t a − s g ( h t b + u θ ( z t b , t a , t b ∣ c ) ⋅ ( t a − t b ) ) ∥ 2 (27) \mathcal{L}{mft-sra} = \left\| h{t_a} - sg\left( h_{t_b} + u_\theta(z_{t_b}, t_a, t_b|c) \cdot (t_a - t_b) \right) \right\|^2 \tag{27} \ Lmft−sra=∥hta−sg(htb+uθ(ztb,ta,tb∣c)⋅(ta−tb))∥2 (27)
3.3 整个架构联合优化+微调
3.3.1 Joint Loss Optimization 联合损失优化
最终的训练目标被构建为多个损失组件的加权和:
L total = L recon + λ flow L MFM + L CSC + λ mae-sra L mae-sra + λ mft-sra L mft-sra (28) \begin{aligned} \mathcal{L}{\text{total}} &= \mathcal{L}{\text{recon}} + \lambda_{\text{flow}} \mathcal{L}{\text{MFM}} \\ &\quad + \mathcal{L}{\text{CSC}} + \lambda_{\text{mae-sra}} \mathcal{L}{\text{mae-sra}} + \lambda{\text{mft-sra}} \mathcal{L}_{\text{mft-sra}} \end{aligned} \tag{28} Ltotal=Lrecon+λflowLMFM+LCSC+λmae-sraLmae-sra+λmft-sraLmft-sra(28)
其中 λ flow \lambda_{\text{flow}} λflow被设为0.5, λ mae-sra \lambda_{\text{mae-sra}} λmae-sra和 λ mft-sra \lambda_{\text{mft-sra}} λmft-sra均被设为0.2。
3.3.2 Flow-Conditioned Fine-Tuning Architecture 流条件微调架构
如图4所示,在微调阶段,利用预训练的MFT 为每个点云组计算流向量。
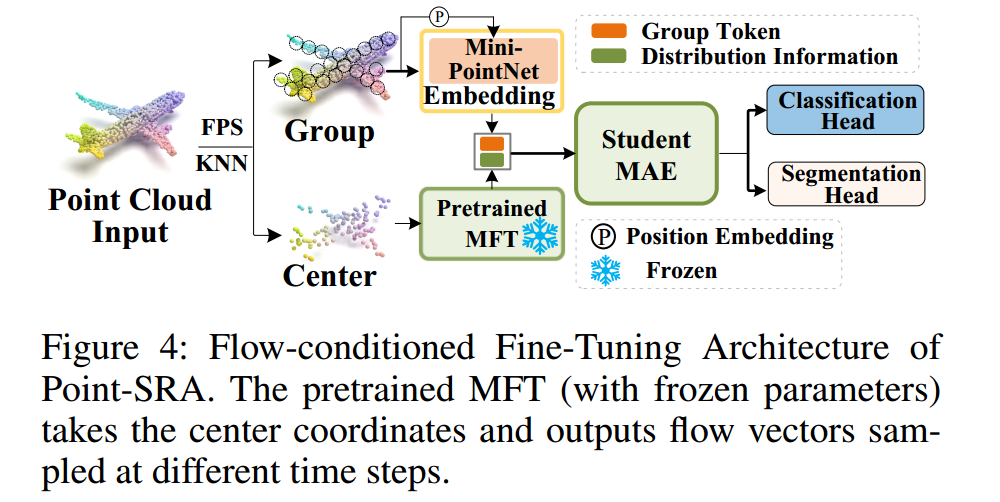
与预训练阶段不同,微调仅使用点云几何信息,不依赖图像或文本模态 :
F u θ = MFT frozen ( Center , t , r ) (29) F_{u_\theta} = \text{MFT}_{\text{frozen}}(\text{Center}, t, r) \tag{29} Fuθ=MFTfrozen(Center,t,r)(29)
其中 Center ∈ R G × 3 \text{Center} \in \mathbb{R}^{G \times 3} Center∈RG×3表示每个点云组的中心坐标, MFT frozen \text{MFT}_{\text{frozen}} MFTfrozen代表参数冻结的预训练MFT模块。时间参数 t t t和 r r r的采样方式与预训练阶段一致。
为将3D流向量投影到特征空间,我们设计了一个专用投影层:
F cond = MLP ( F u θ + ∥ F u θ ∥ 2 ) (30) F_{\text{cond}} = \text{MLP}\left(F_{u_\theta} +\| F_{u_\theta} \|_2\right) \tag{30} Fcond=MLP(Fuθ+∥Fuθ∥2)(30)
其中 ∥ F u θ ∥ 2 \| F_{u_\theta} \|_2 ∥Fuθ∥2是流向量的L2范数,通过元素级广播操作匹配维度。
此外,引入自适应门控机制来控制流条件对原始组特征的影响:
g = σ ( MLP gate ( F cond ) ) (31) g = \sigma\left(\text{MLP}{\text{gate}}(F{\text{cond}})\right) \tag{31} g=σ(MLPgate(Fcond))(31)
H Θ = H g ⊙ ( 1 + α g ) + β F cond (32) H_\Theta = H_g \odot (1 + \alpha g) + \beta F_{\text{cond}} \tag{32} HΘ=Hg⊙(1+αg)+βFcond(32)
其中 H g H_g Hg是原始组特征, g ∈ [ 0 , 1 ] G × d g \in [0,1]^{G \times d} g∈[0,1]G×d是学习得到的门控值, α 、 β \alpha、\beta α、β是可训练的调制参数,运算符 ⊙ \odot ⊙表示元素级调制。
4. Experiments 实验部分
4.1 下游任务
4.1.1 Object Classification 物体分类
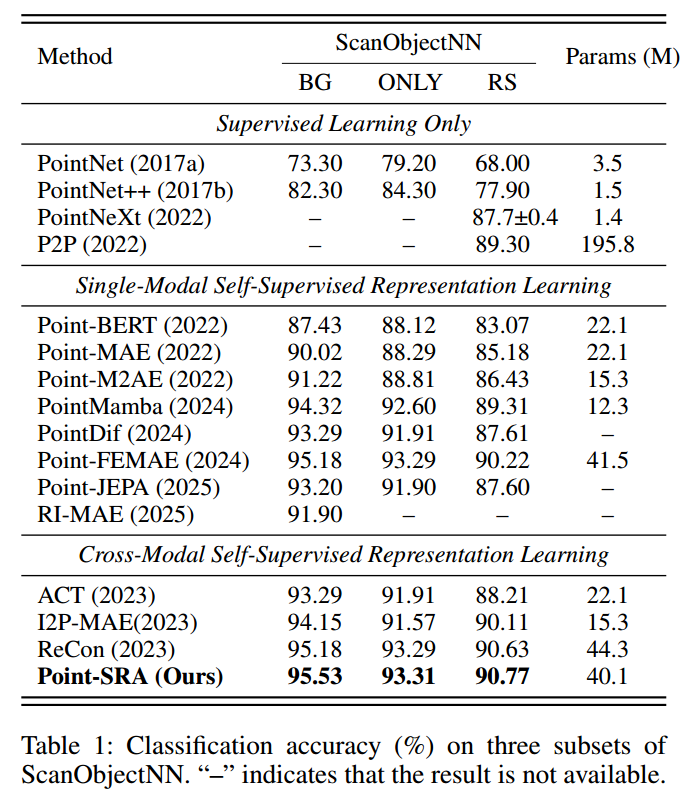
在真实世界物体分类基准数据集ScanObjectNN(Uy等人,2019)上评估预训练模型:该数据集包含15个类别共1.5万个点云物体,分为三个子集------OBJ_BG(含背景的物体)、OBJ_ONLY(仅物体)、PB_T50_RS(含背景与人为扰动的物体)。
如表1所示,我们的方法在这三个子集上的整体准确率分别达到95.53%、93.31%、90.77%,相比Point-MAE(Pang等人,2022)分别提升了+5.51%、+5.02%、+5.59%。
4.1.2 Intracranial Aneurysm Classification and Segmentation. 颅内动脉瘤分类与分割
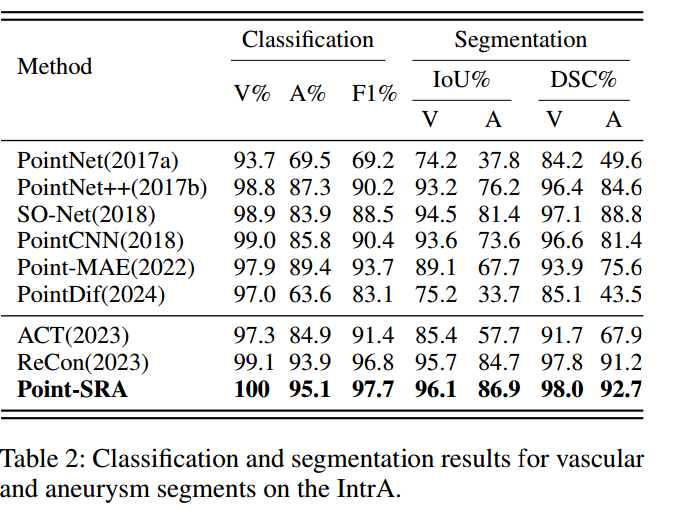
IntrA数据集(Yang等人,2020)包含1909个血管段,其中1694个健康血管段、215个动脉瘤血管段。主要评估指标为F1分数(F1):V和A分别代表健康颅内血管与动脉瘤的分类准确率;交并比(IoU)和Dice相似系数(DSC) 用于评估血管与动脉瘤区域的分割性能。
如表2所示,Point-SRA的F1分数达97.7,优于Point-MAE(提升4)与多模态ACT方法(Dong等人,2023,提升6.3);在分割任务中,Point-SRA在动脉瘤区域的IoU达86.9%、DSC达92.7%,显著超过主流分割基线模型。
4.1.3 Few-Shot Classification 少样本分类
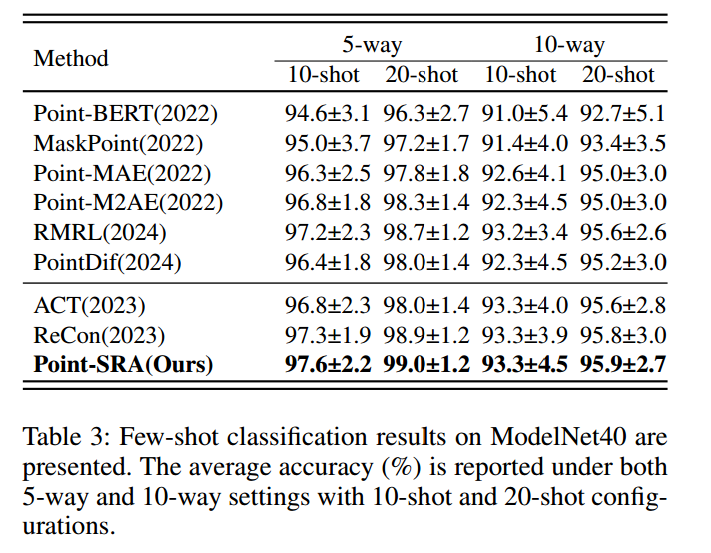
在ModelNet40数据集(Wu等人,2015)的少样本学习场景下开展系统实验。
如表3所示:在5分类配置中,Point-SRA在10-shot、20-shot设置下的平均准确率分别达97.6%、99.0%,相比Point-MAE基线(Pang等人,2022)分别提升1.3%、1.2%;在10分类配置中,Point-SRA在10-shot、20-shot设置下的准确率分别达93.3%、95.9%。
4.1.4 3D Object Detection. 3D物体检测
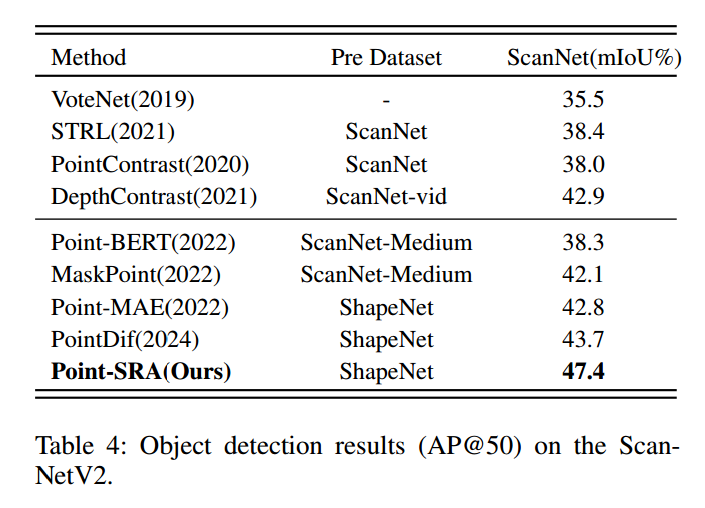
在ScanNetV2数据集(Dai等人,2017)的室内场景检测任务中,采用基于MinkowskiEngine(Choy、Gwak与Savarese,2019)的3D稀疏卷积网络作为骨干,并将Point-SRA预训练编码器集成到特征提取流程中。
ScanNetV2包含1513个完整扫描的室内场景,覆盖18个常见物体类别。我们遵循标准平均精度(AP)指标,在IoU阈值0.5(AP@50)下进行评估。如表4所示,Point-SRA预训练编码器的AP@50达47.4%,
这一提升主要源于对复杂几何结构物体的定位与识别更精准,体现了Point-SRA的几何特征表示在建模空间复杂性方面的有效性。
4.1.5 Indoor Scene Segmentation. 室内场景分割
S3DIS数据集(Armeni等人,2020)包含6个大型室内区域,共271个房间,涵盖13个语义类别与家具物体。我们遵循标准Area-5评估协议:以Area-5为测试集,其余区域为训练集。
实验中采用基于MinkowskiEngine(Choy、Gwak与Savarese,2019)的稀疏卷积网络作为骨干,保持解码器架构与分割头不变,仅将编码器替换为预训练的Point-SRA模型。训练时冻结Point-SRA编码器,仅微调解码器与分割头;使用AdamW优化器,初始学习率0.006、权重衰减0.05,训练100个epoch。
如表5所示,Point-SRA在S3DIS测试集上的mIoU达71.8%、mAcc达79.3%。
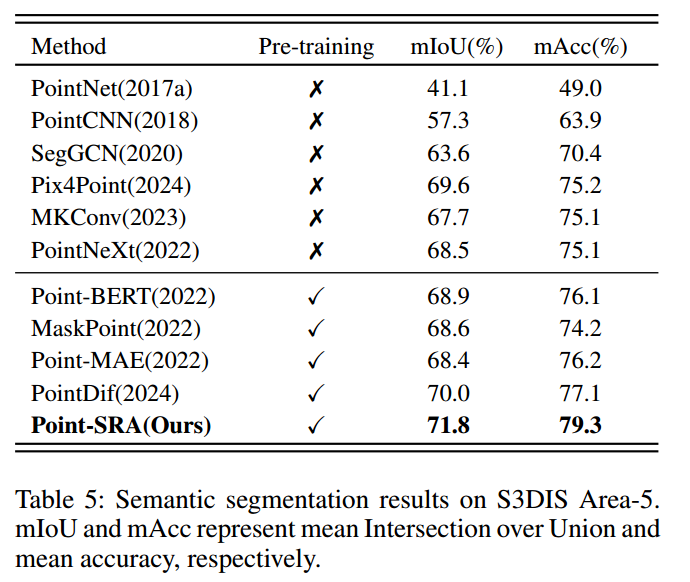
4.2 Ablation Study 消融实验
4.2.1 Effectiveness of Core Components 核心组件的有效性
逐步移除Point-SRA的关键组件,以量化每个模块对最终性能的贡献。以Point-MAE为基线,所有组件均采用流条件微调架构。
表6展示了不同组件组合下的性能表现:MeanFlow带来了显著提升,使PB_T50_RS子集的准确率提高了5.45%,验证了概率重构相比逐点重构的有效性。
与基线MAE相比,完整的Point-SRA框架在所有任务上均实现了大幅性能提升,证明了组件集成的有效性与整体设计的合理性。
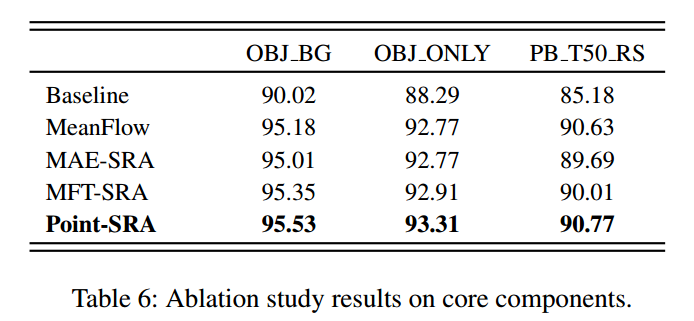
4.2.2 Flow-Conditioned Fine-Tuning Architecture 流条件微调架构
表7展示了流条件微调增强对下游性能的具体影响:首先通过流条件投影层,将预训练MFT的几何分布转换到特征对齐空间;随后引入可学习的门控融合机制,自适应控制融合强度,让网络动态利用预训练知识。
单独使用投影或门控仅能带来有限提升,而两者结合(FULL)将分割性能提升至84.88%,相比基线提高了0.61%。
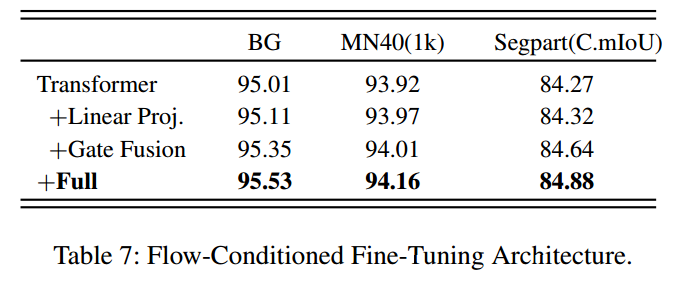
4.2.3 Comparison of Probabilistic Modeling Methods 概率建模方法的对比
为验证MeanFlow相比其他概率生成方法的优越性,在相同实验设置下对比了多种概率建模技术。
表8展示了不同方法的性能结果。
在分类准确率方面,MeanFlow达到了最高精度,优于扩散模型及其他流匹配方法。
在数值稳定性上,时间区间MeanFlow 有效降低了预训练过程中的梯度方差,使训练更稳定可靠。
具体而言,它满足以下不等式:
Var [ u t , s ( z t ) ] ≤ 1 ( s − t ) 2 ∫ t s Var [ v τ ( z τ ) ] d τ (33) \text{Var}\left[\mathbf{u}{t,s}(\mathbf{z}t)\right] \leq \frac{1}{(s-t)^2} \int_t^s \text{Var}\left[\mathbf{v}\tau(\mathbf{z}\tau)\right]d\tau \tag{33} Var[ut,s(zt)]≤(s−t)21∫tsVar[vτ(zτ)]dτ(33)
其中 v τ ( z τ ) \mathbf{v}\tau(\mathbf{z}\tau) vτ(zτ)表示时间 τ \tau τ处的瞬时速度场,详细证明见补充材料中的定理C。
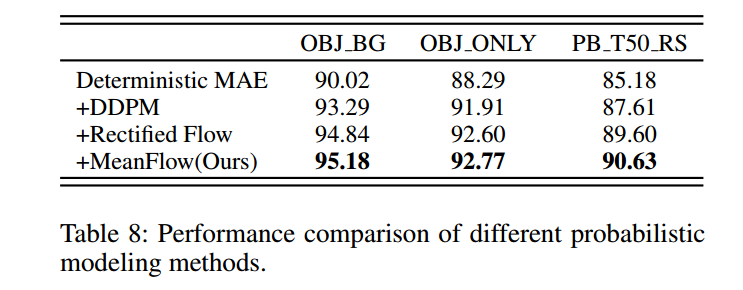
4.2.4 MFT Hyperparameter MFT超参数
系统分析了MFT的关键设计选择,包括网络块、时间采样策略与损失函数。
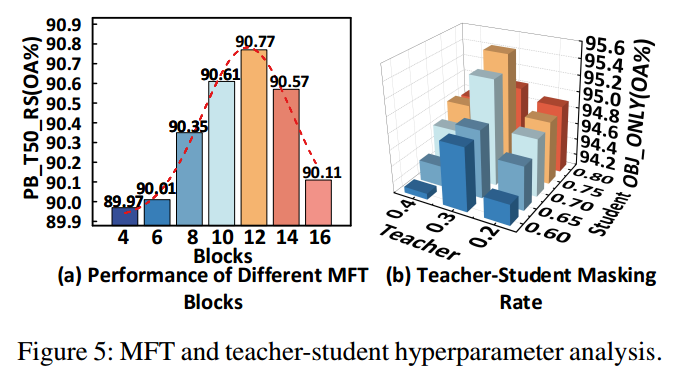
如图5(a)所示,12层MFT块在性能与计算成本之间实现了最佳权衡。
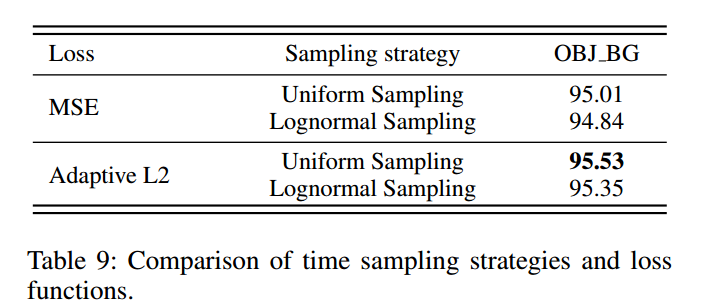
表9对比了不同时间调度方法:在区间 [ 0 , 1 ] [0,1] [0,1]上的均匀采样为MeanFlow提供了最稳定的训练信号,性能优于对数正态采样。
在损失函数方面,自适应L2损失利用加权机制更好地处理样本间的损失差异,相比MSE损失实现了更稳定、高效的优化。
4.2.5 Mask Ratio Configuration 掩码率配置
图5(b)展示了不同掩码率设置对性能的影响:最优配置为教师模型采用30%掩码率、学生模型采用75%掩码率,以此取得最佳结果。
该设置使教师模型保留丰富的几何细节,同时让学生模型专注于学习更高层次的语义抽象。
约0.45的掩码率差能实现最佳平衡:差值过小会导致互补性不足,差值过大则会增加对齐难度、降低知识迁移效果。
5. Related Work 相关工作
Point-MAE(Pang等人,2022)与Point-M2AE(Zhang等人,2022)将MAE应用于点云,采用固定或多尺度掩码策略,但在几何多样性与逐点重构方面存在不足。MaskPoint(Liu、Cai与Lee,2022)引入了几何感知掩码;PTM(Cheng等人,2024)与Point-FEMAE(Zha等人,2024)提出了密度或并行掩码策略,但这些方法均涉及复杂的微调或有限的语义理解。ReCon(Qi等人,2023)提出三模态对比学习,以增强3D MAE的语义表示能力。
流匹配(Lipman等人,2023)支持直接学习概率流;MeanFlow(Geng等人,2025)通过平均速度预测提升了训练稳定性。PointFM(Cheng等人,2025)将校正流匹配应用于点云表示学习,但需要精心设计流预测器,且存在训练不稳定的问题。
REPA(Yu等人,2024)等方法证明了自蒸馏与跨阶段对齐的优势;I-DAE(Chen等人,2025)表明扩散模型的隐藏状态可学习判别性表示。
我们的工作基于这些研究思路,提出了一种统一的双重自表示对齐机制,覆盖了不同掩码率与时间状态。
6. Conclusion 结论
本文提出了Point-SRA这一自监督表示学习框架:首先,通过系统性研究揭示了不同掩码率的互补特征;其次,创新性地将MeanFlow用于3D自监督表示学习(3D SSL),实现了概率建模与表示引导;此外,结合掩码率对齐与MeanFlow时间对齐,设计了双重自表示对齐机制;最后,构建了专用的微调网络,通过流向量条件融合,充分利用预训练阶段学到的几何分布知识。
大量实验验证了Point-SRA的有效性,其在多个标准基准数据集上取得了优异结果。未来工作将聚焦于探索高效的隐状态知识蒸馏方法,以进一步推动3D自监督表示学习的发展。